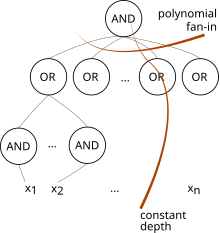
AC is a complexity class used in circuit complexity. It is the smallest class in the AC hierarchy, and consists of all families of circuits of depth O(1) and polynomial size, with unlimited-fanin AND gates and OR gates (we allow NOT gates only at the inputs). It thus contains NC, which has only bounded-fanin AND and OR gates.
Example problems
Integer addition and subtraction are computable in AC, but multiplication is not (specifically, when the inputs are two integers under the usual binary or base-10 representations of integers).
Since it is a circuit class, like P/poly, AC also contains every unary language.
Descriptive complexity
From a descriptive complexity viewpoint, DLOGTIME-uniform AC is equal to the descriptive class FO+BIT of all languages describable in first-order logic with the addition of the BIT predicate, or alternatively by FO(+, ×), or by Turing machine in the logarithmic hierarchy.
Separations
In 1984 Furst, Saxe, and Sipser showed that calculating the parity of the input bits (unlike the aforementioned addition/subtraction problems above which had two inputs) cannot be decided by any AC circuits, even with non-uniformity. It follows that AC is not equal to NC, because a family of circuits in the latter class can compute parity. More precise bounds follow from switching lemma. Using them, it has been shown that there is an oracle separation between the polynomial hierarchy and PSPACE.
References
- ^ Arora, Sanjeev; Barak, Boaz (2009). Computational complexity. A modern approach. Cambridge University Press. pp. 117–118, 287. ISBN 978-0-521-42426-4. Zbl 1193.68112.
- Barrington, David Mix; Maciel, Alexis (July 18, 2000). "Lecture 2: The Complexity of Some Problems" (PDF). IAS/PCMI Summer Session 2000, Clay Mathematics Undergraduate Program: Basic Course on Computational Complexity.
- Kayal, Neeraj; Hegde, Sumant (2015). "Lecture 5: Feb 4, 2015" (PDF). E0 309: Topics in Complexity Theory. Archived (PDF) from the original on 2021-10-16. Retrieved 2021-10-16.
- Immerman, N. (1999). Descriptive Complexity. Springer. p. 85.
- Furst, Merrick; Saxe, James B.; Sipser, Michael (1984). "Parity, circuits, and the polynomial-time hierarchy". Mathematical Systems Theory. 17 (1): 13–27. doi:10.1007/BF01744431. MR 0738749. Zbl 0534.94008.
| Complexity classes | |
|---|---|
| Considered feasible | |
| Suspected infeasible | |
| Considered infeasible | |
| Class hierarchies | |
| Families of classes | |
| List of complexity classes | |