| Bitruncated cubic honeycomb | |
|---|---|
 
| |
| Type | Uniform honeycomb |
| Schläfli symbol | 2t{4,3,4} t1,2{4,3,4} |
| Coxeter-Dynkin diagram | |
| Cell type | (4.6.6) |
| Face types | square {4} hexagon {6} |
| Edge figure | isosceles triangle {3} |
| Vertex figure |  (tetragonal disphenoid) |
| Space group Fibrifold notation Coxeter notation |
Im3m (229) 8:2 ] |
| Coxeter group | , |
| Dual | Oblate tetrahedrille Disphenoid tetrahedral honeycomb Cell: 
|
| Properties | isogonal, isotoxal, isochoric |

The bitruncated cubic honeycomb is a space-filling tessellation (or honeycomb) in Euclidean 3-space made up of truncated octahedra (or, equivalently, bitruncated cubes). It has 4 truncated octahedra around each vertex. Being composed entirely of truncated octahedra, it is cell-transitive. It is also edge-transitive, with 2 hexagons and one square on each edge, and vertex-transitive. It is one of 28 uniform honeycombs.
John Horton Conway calls this honeycomb a truncated octahedrille in his Architectonic and catoptric tessellation list, with its dual called an oblate tetrahedrille, also called a disphenoid tetrahedral honeycomb. Although a regular tetrahedron can not tessellate space alone, this dual has identical disphenoid tetrahedron cells with isosceles triangle faces.
Geometry
It can be realized as the Voronoi tessellation of the body-centred cubic lattice. Lord Kelvin conjectured that a variant of the bitruncated cubic honeycomb (with curved faces and edges, but the same combinatorial structure) was the optimal soap bubble foam. However, a number of less symmetrical structures have later been found to be more efficient foams of soap bubbles, among which the Weaire–Phelan structure appears to be the best.
The honeycomb represents the permutohedron tessellation for 3-space. The coordinates of the vertices for one octahedron represent a hyperplane of integers in 4-space, specifically permutations of (1,2,3,4). The tessellation is formed by translated copies within the hyperplane.
The tessellation is the highest tessellation of parallelohedrons in 3-space.
Projections
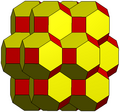
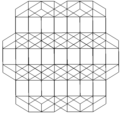
The bitruncated cubic honeycomb can be orthogonally projected into the euclidean plane with various symmetry arrangements. The highest (hexagonal) symmetry form projects into a nonuniform rhombitrihexagonal tiling. A square symmetry projection forms two overlapping truncated square tiling, which combine together as a chamfered square tiling.
| Symmetry | p6m (*632) | p4m (*442) | pmm (*2222) | ||
|---|---|---|---|---|---|
| Solid | 
|

|

|

|
|
| Frame | 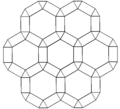
|

|

|
|

|
Symmetry
The vertex figure for this honeycomb is a disphenoid tetrahedron, and it is also the Goursat tetrahedron (fundamental domain) for the Coxeter group. This honeycomb has four uniform constructions, with the truncated octahedral cells having different Coxeter groups and Wythoff constructions. These uniform symmetries can be represented by coloring differently the cells in each construction.
| Space group | Im3m (229) | Pm3m (221) | Fm3m (225) | F43m (216) | Fd3m (227) |
|---|---|---|---|---|---|
| Fibrifold | 8:2 | 4:2 | 2:2 | 1:2 | 2:2 |
| Coxeter group | ×2 ] =] |
=] |
=<> |
×2 ] =] | |
| Coxeter diagram | |||||
| truncated octahedra | 1 |
1:1 |
2:1:1 |
1:1:1:1 |
1:1 |
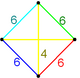
| Vertex figure | 
|

|

|
|

|
| Vertex figure symmetry |
(order 8) |
(order 4) |
(order 2) |
(order 1) |
(order 2) |
| Image Colored by cell |

|

|

|

|

|
Related polyhedra and honeycombs

The , ![]()
![]()
![]()
![]()
![]()
![]()
![]() , Coxeter group generates 15 permutations of uniform tessellations, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.
, Coxeter group generates 15 permutations of uniform tessellations, 9 with distinct geometry including the alternated cubic honeycomb. The expanded cubic honeycomb (also known as the runcinated tesseractic honeycomb) is geometrically identical to the cubic honeycomb.
| C3 honeycombs | |||||
|---|---|---|---|---|---|
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
| Pm3m (221) |
4:2 | ×1 | |||
| Fm3m (225) |
2:2 | ↔ |
↔ |
Half | |
| I43m (217) |
4:2 | ] | Half × 2 | ||
| Fd3m (227) |
2:2 | ] ↔ ] |
↔ |
Quarter × 2 | |
| Im3m (229) |
8:2 | ] | ×2 | ||
The , ![]()
![]()
![]()
![]()
![]() , Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.
, Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.
| B3 honeycombs | |||||
|---|---|---|---|---|---|
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
| Fm3m (225) |
2:2 | ↔ |
↔ |
×1 | |
| Fm3m (225) |
2:2 | <> ↔ <> |
↔ |
×2 | |
| Pm3m (221) |
4:2 | <> | ×2 | ||
This honeycomb is one of five distinct uniform honeycombs constructed by the Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:
| A3 honeycombs | ||||||
|---|---|---|---|---|---|---|
| Space group |
Fibrifold | Square symmetry |
Extended symmetry |
Extended diagram |
Extended group |
Honeycomb diagrams |
| F43m (216) |
1:2 | a1 |
(None) | |||
| Fm3m (225) |
2:2 | d2 |
<> ↔ |
↔ |
×21 ↔ |
|
| Fd3m (227) |
2:2 | g2 |
] or ] |
↔ |
×22 | |
| Pm3m (221) |
4:2 | d4 |
<2> ↔ |
↔ |
×41 ↔ |
|
| I3 (204) |
8 | r8 |
] ↔ ] |
↔ |
½×8 ↔ ½×2 |
|
| Im3m (229) |
8:2 | ] ↔ ] |
×8 ↔ ×2 |
|||
Alternated form
| Alternated bitruncated cubic honeycomb | |
|---|---|
| Type | Convex honeycomb |
| Schläfli symbol | 2s{4,3,4} 2s{4,3} sr{3} |
| Coxeter diagrams | |
| Cells | tetrahedron icosahedron |
| Vertex figure | 
|
| Coxeter group | ], |
| Dual | Ten-of-diamonds honeycomb Cell: 
|
| Properties | vertex-transitive |
This honeycomb can be alternated, creating pyritohedral icosahedra from the truncated octahedra with disphenoid tetrahedral cells created in the gaps. There are three constructions from three related Coxeter-Dynkin diagrams: ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]() , and
, and ![]()
![]()
![]()
![]()
![]() . These have symmetry , and respectively. The first and last symmetry can be doubled as ] and ].
. These have symmetry , and respectively. The first and last symmetry can be doubled as ] and ].
The dual honeycomb is made of cells called ten-of-diamonds decahedra.
| Space group | I3 (204) | Pm3 (200) | Fm3 (202) | Fd3 (203) | F23 (196) |
|---|---|---|---|---|---|
| Fibrifold | 8 | 4 | 2 | 2 | 1 |
| Coxeter group | ] | ] | |||
| Coxeter diagram | |||||
| Order | double | full | half | quarter double |
quarter |
| Image colored by cells |

|

|

|

|

|
This honeycomb is represented in the boron atoms of the α-rhombohedral crystal. The centers of the icosahedra are located at the fcc positions of the lattice.
Related polytopes
Nonuniform variants with symmetry and two types of truncated octahedra can be doubled by placing the two types of truncated octahedra to produce a nonuniform honeycomb with truncated octahedra and hexagonal prisms (as ditrigonal trapezoprisms). Its vertex figure is a C2v-symmetric triangular bipyramid.
This honeycomb can then be alternated to produce another nonuniform honeycomb with pyritohedral icosahedra, octahedra (as triangular antiprisms), and tetrahedra (as sphenoids). Its vertex figure has C2v symmetry and consists of 2 pentagons, 4 rectangles, 4 isosceles triangles (divided into two sets of 2), and 4 scalene triangles.
See also
Notes
- , A000029 6-1 cases, skipping one with zero marks
- Williams, 1979, p 199, Figure 5-38.
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, (1.9 Uniform space-fillings)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- Klitzing, Richard. "3D Euclidean Honeycombs o4x3x4o - batch - O16".
- Uniform Honeycombs in 3-Space: 05-Batch
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.
 ,
,



