| Alternated order-4 hexagonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | (3.4) |
| Schläfli symbol | h{6,4} or (3,4,4) |
| Wythoff symbol | 4 | 3 4 |
| Coxeter diagram | |
| Symmetry group | , (*443) |
| Dual | Order-4-4-3_t0 dual tiling |
| Properties | Vertex-transitive |
In geometry, the alternated order-4 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of (3,4,4), h{6,4}, and hr{6,6}.
Uniform constructions
There are four uniform constructions, with some of lower ones which can be seen with two colors of triangles:
| *443 | 3333 | *3232 | 3*22 |
|---|---|---|---|

|

| ||
| (4,4,3) = h{6,4} | hr{6,6} = h{6,4}1⁄2 | ||
Related polyhedra and tiling
| Uniform tetrahexagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: , (*642) (with (*662), (*443) , (*3222) index 2 subsymmetries) (And (*3232) index 4 subsymmetry) | |||||||||||
= = = |
= |
= = = |
= |
= = = |
= |
||||||

|

|

|

|

|

|

| |||||
| {6,4} | t{6,4} | r{6,4} | t{4,6} | {4,6} | rr{6,4} | tr{6,4} | |||||
| Uniform duals | |||||||||||

|

|

|

|

|

|

| |||||
| V6 | V4.12.12 | V(4.6) | V6.8.8 | V4 | V4.4.4.6 | V4.8.12 | |||||
| Alternations | |||||||||||
(*443) |
(6*2) |
(*3222) |
(4*3) |
(*662) |
(2*32) |
(642) | |||||
= |
= |
= |
= |
= |
= |
||||||

|

|

|

|

|

|

| |||||
| h{6,4} | s{6,4} | hr{6,4} | s{4,6} | h{4,6} | hrr{6,4} | sr{6,4} | |||||
| Uniform hexahexagonal tilings | ||||||
|---|---|---|---|---|---|---|
| Symmetry: , (*662) | ||||||
= |
= |
= |
= |
= |
= |
= |

|
|

|

|

|

|

|
| {6,6} = h{4,6} |
t{6,6} = h2{4,6} |
r{6,6} {6,4} |
t{6,6} = h2{4,6} |
{6,6} = h{4,6} |
rr{6,6} r{6,4} |
tr{6,6} t{6,4} |
| Uniform duals | ||||||

|

|

|

|

|

|

|
| V6 | V6.12.12 | V6.6.6.6 | V6.12.12 | V6 | V4.6.4.6 | V4.12.12 |
| Alternations | ||||||
(*663) |
(6*3) |
(*3232) |
(6*3) |
(*663) |
(2*33) |
(662) |

|

|

|

|

| ||
| h{6,6} | s{6,6} | hr{6,6} | s{6,6} | h{6,6} | hrr{6,6} | sr{6,6} |
| Uniform (4,4,3) tilings | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: (*443) | (443) |
(3*22) |
(*3232) | |||||||

|

|

|

|

|

|

|

|

|

|

|
| h{6,4} t0(4,4,3) |
h2{6,4} t0,1(4,4,3) |
{4,6}/2 t1(4,4,3) |
h2{6,4} t1,2(4,4,3) |
h{6,4} t2(4,4,3) |
r{6,4}/2 t0,2(4,4,3) |
t{4,6}/2 t0,1,2(4,4,3) |
s{4,6}/2 s(4,4,3) |
hr{4,6}/2 hr(4,3,4) |
h{4,6}/2 h(4,3,4) |
q{4,6} h1(4,3,4) |
| Uniform duals | ||||||||||

|

|

|

|
|||||||
| V(3.4) | V3.8.4.8 | V(4.4) | V3.8.4.8 | V(3.4) | V4.6.4.6 | V6.8.8 | V3.3.3.4.3.4 | V(4.4.3) | V6 | V4.3.4.6.6 |
| Similar H2 tilings in *3232 symmetry | ||||||||
|---|---|---|---|---|---|---|---|---|
| Coxeter diagrams |
||||||||
| Vertex figure |
6 | (3.4.3.4) | 3.4.6.6.4 | 6.4.6.4 | ||||
| Image | 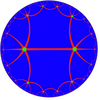
|

|

|

| ||||
| Dual | 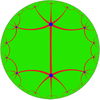
|

| ||||||
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
See also
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery Archived 2013-03-24 at the Wayback Machine
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
| Tessellation | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|   | ||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
This hyperbolic geometry-related article is a stub. You can help Misplaced Pages by expanding it. |