In computer architecture, Amdahl's law (or Amdahl's argument) is a formula that shows how much faster a task can be completed when you add more resources to the system.
The law can be stated as:
"the overall performance improvement gained by optimizing a single part of a system is limited by the fraction of time that the improved part is actually used".
It is named after computer scientist Gene Amdahl, and was presented at the American Federation of Information Processing Societies (AFIPS) Spring Joint Computer Conference in 1967.
Amdahl's law is often used in parallel computing to predict the theoretical speedup when using multiple processors.
Definition
In the context of Amdahl's law, speedup can be defined as:
or
Amdahl's law can be formulated in the following way:
where
- represents the total speedup of a program
- represents time spent on the code where parallelism is used
- represents the extent of the improvement
The is frequently much lower than one might expect. For instance, if a programmer enhances a part of the code that represents 10% of the total execution time (i.e. of 0.10) and achieves a of 10,000, then becomes 1.11 which means only 11% improvement in total speedup of the program. So, despite a massive improvement in one section, the overall benefit is quite small. In another example, if the programmer optimizes a section that accounts for 99% of the execution time (i.e. of 0.99) with a speedup factor of 100 (i.e. of 100), the only reaches 50. This indicates that half of the potential performance gain ( will reach 100 if 100% of the execution time is covered) is lost due to the remaining 1% of execution time that was not improved.
Implications
Followings are implications of Amdahl's law:
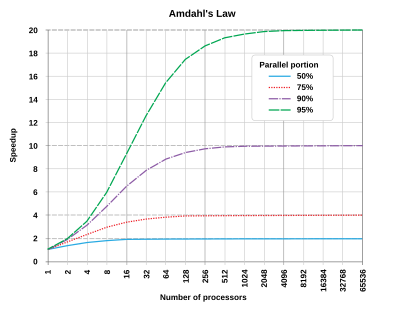
- Diminishing Returns: Adding more processors gives diminishing returns. Beyond a certain point, adding more processors doesn't significantly increase speedup.
- Limited Speedup: Even with many processors, there's a limit to how much faster a task can be completed due to parts of the task that cannot be parallelized.
Limitations
Followings are limitations of Amdahl's law:
- Assumption of Fixed Workload: Amdahl's Law assumes that the workload remains constant. It doesn't account for dynamic or increasing workloads, which can impact the effectiveness of parallel processing.
- Overhead Ignored: Amdahl's Law neglects overheads associated with concurrency, including coordination, synchronization, inter-process communication, and concurrency control. Notably, merging data from multiple threads or processes incurs significant overhead due to conflict resolution, data consistency, versioning, and synchronization.
- Neglecting extrinsic factors: Amdahl's Law addresses computational parallelism, neglecting extrinsic factors such as data persistence, I/O operations, and memory access overheads, and assumes idealized conditions.
- Scalability Issues: While it highlights the limits of parallel speedup, it doesn't address practical scalability issues, such as the cost and complexity of adding more processors.
- Non-Parallelizable Work: Amdahl's Law emphasizes the non-parallelizable portion of the task as a bottleneck but doesn’t provide solutions for reducing or optimizing this portion.
- Assumes Homogeneous Processors: It assumes that all processors are identical and contribute equally to speedup, which may not be the case in heterogeneous computing environments.
Amdahl's law applies only to the cases where the problem size is fixed. In practice, as more computing resources become available, they tend to get used on larger problems (larger datasets), and the time spent in the parallelizable part often grows much faster than the inherently serial work. In this case, Gustafson's law gives a less pessimistic and more realistic assessment of the parallel performance.
Universal Scalability Law (USL), developed by Neil J. Gunther, extends the Amdahl's law and accounts for the additional overhead due to inter-process communication. USL quantifies scalability based on parameters such as contention and coherency.
Derivation
A task executed by a system whose resources are improved compared to an initial similar system can be split up into two parts:
- a part that does not benefit from the improvement of the resources of the system;
- a part that benefits from the improvement of the resources of the system.
An example is a computer program that processes files. A part of that program may scan the directory of the disk and create a list of files internally in memory. After that, another part of the program passes each file to a separate thread for processing. The part that scans the directory and creates the file list cannot be sped up on a parallel computer, but the part that processes the files can.
The execution time of the whole task before the improvement of the resources of the system is denoted as . It includes the execution time of the part that would not benefit from the improvement of the resources and the execution time of the one that would benefit from it. The fraction of the execution time of the task that would benefit from the improvement of the resources is denoted by . The one concerning the part that would not benefit from it is therefore . Then:
It is the execution of the part that benefits from the improvement of the resources that is accelerated by the factor after the improvement of the resources. Consequently, the execution time of the part that does not benefit from it remains the same, while the part that benefits from it becomes:
The theoretical execution time of the whole task after the improvement of the resources is then:
Amdahl's law gives the theoretical speedup in latency of the execution of the whole task at fixed workload , which yields
Parallel programs
If 30% of the execution time may be the subject of a speedup, p will be 0.3; if the improvement makes the affected part twice as fast, s will be 2. Amdahl's law states that the overall speedup of applying the improvement will be:
For example, assume that we are given a serial task which is split into four consecutive parts, whose percentages of execution time are p1 = 0.11, p2 = 0.18, p3 = 0.23, and p4 = 0.48 respectively. Then we are told that the 1st part is not sped up, so s1 = 1, while the 2nd part is sped up 5 times, so s2 = 5, the 3rd part is sped up 20 times, so s3 = 20, and the 4th part is sped up 1.6 times, so s4 = 1.6. By using Amdahl's law, the overall speedup is
Notice how the 5 times and 20 times speedup on the 2nd and 3rd parts respectively don't have much effect on the overall speedup when the 4th part (48% of the execution time) is accelerated by only 1.6 times.
Serial programs

For example, with a serial program in two parts A and B for which TA = 3 s and TB = 1 s,
- if part B is made to run 5 times faster, that is s = 5 and p = TB/(TA + TB) = 0.25, then
- if part A is made to run 2 times faster, that is s = 2 and p = TA/(TA + TB) = 0.75, then
Therefore, making part A to run 2 times faster is better than making part B to run 5 times faster. The percentage improvement in speed can be calculated as
- Improving part A by a factor of 2 will increase overall program speed by a factor of 1.60, which makes it 37.5% faster than the original computation.
- However, improving part B by a factor of 5, which presumably requires more effort, will achieve an overall speedup factor of 1.25 only, which makes it 20% faster.
Optimizing the sequential part of parallel programs
If the non-parallelizable part is optimized by a factor of , then
It follows from Amdahl's law that the speedup due to parallelism is given by
When , we have , meaning that the speedup is measured with respect to the execution time after the non-parallelizable part is optimized.
When ,
If , and , then:
Transforming sequential parts of parallel programs into parallelizable
Next, we consider the case wherein the non-parallelizable part is reduced by a factor of , and the parallelizable part is correspondingly increased. Then
It follows from Amdahl's law that the speedup due to parallelism is given by
Relation to the law of diminishing returns
Amdahl's law is often conflated with the law of diminishing returns, whereas only a special case of applying Amdahl's law demonstrates law of diminishing returns. If one picks optimally (in terms of the achieved speedup) what is to be improved, then one will see monotonically decreasing improvements as one improves. If, however, one picks non-optimally, after improving a sub-optimal component and moving on to improve a more optimal component, one can see an increase in the return. Note that it is often rational to improve a system in an order that is "non-optimal" in this sense, given that some improvements are more difficult or require larger development time than others.
Amdahl's law does represent the law of diminishing returns if one is considering what sort of return one gets by adding more processors to a machine, if one is running a fixed-size computation that will use all available processors to their capacity. Each new processor added to the system will add less usable power than the previous one. Each time one doubles the number of processors the speedup ratio will diminish, as the total throughput heads toward the limit of 1/(1 − p).
This analysis neglects other potential bottlenecks such as memory bandwidth and I/O bandwidth. If these resources do not scale with the number of processors, then merely adding processors provides even lower returns.
An implication of Amdahl's law is that to speed up real applications which have both serial and parallel portions, heterogeneous computing techniques are required. There are novel speedup and energy consumption models based on a more general representation of heterogeneity, referred to as the normal form heterogeneity, that support a wide range of heterogeneous many-core architectures. These modelling methods aim to predict system power efficiency and performance ranges, and facilitates research and development at the hardware and system software levels.
See also
- Gustafson's law
- Universal Law of Computational Scalability
- Analysis of parallel algorithms
- Critical path method
- Moore's law
References
- Rodgers, David P. (June 1985). "Improvements in multiprocessor system design". ACM SIGARCH Computer Architecture News. 13 (3). New York, NY, USA: ACM: 225–231 . doi:10.1145/327070.327215. ISBN 0-8186-0634-7. ISSN 0163-5964. S2CID 7083878.
- Reddy, Martin (2011). API Design for C++. Burlington, Massachusetts: Morgan Kaufmann Publishers. p. 210. doi:10.1016/C2010-0-65832-9. ISBN 978-0-12-385003-4. LCCN 2010039601. OCLC 666246330.
- ^ Computer Architecture: A Quantitative Approach. Morgan Kaufmann. 2003. ISBN 978-8178672663.
- ^ Bakos, Jason D. (2016-01-01), Bakos, Jason D. (ed.), "Chapter 2 - Multicore and data-level optimization: OpenMP and SIMD", Embedded Systems, Boston: Morgan Kaufmann, pp. 49–103, doi:10.1016/b978-0-12-800342-8.00002-x, ISBN 978-0-12-800342-8, retrieved 2024-11-18
- The Art of Multiprocessor Programming, Revised Reprint. Morgan Kaufmann. 22 May 2012. ISBN 9780123973375.
- Vajda, András (10 June 2011). Programming Many-Core Chips. Springer. ISBN 9781441997395.
- Amdahl, Gene M. (1967-04-18). "Validity of the single processor approach to achieving large scale computing capabilities". Proceedings of the April 18-20, 1967, spring joint computer conference on - AFIPS '67 (Spring). New York, NY, USA: Association for Computing Machinery. pp. 483–485. doi:10.1145/1465482.1465560. ISBN 978-1-4503-7895-6.
- Parallel Computer Architecture A Hardware/Software Approach. Elsevier Science. 1999. ISBN 9781558603431.
- Concurrent Programming: Algorithms, Principles, and Foundations. Springer. 23 December 2012. ISBN 978-3642320262.
- McCool, Michael; Reinders, James; Robison, Arch (2013). Structured Parallel Programming: Patterns for Efficient Computation. Elsevier. p. 61. ISBN 978-0-12-415993-8.
- Gunther, Neil (2007). Guerrilla Capacity Planning: A Tactical Approach to Planning for Highly Scalable Applications and Services. ISBN 978-3540261384.
- Hill, Mark D.; Marty, Michael R. (2008). "Amdahl's Law in the Multicore Era". Computer. 41 (7): 33–38. CiteSeerX 10.1.1.221.8635. doi:10.1109/MC.2008.209.
- Rafiev, Ashur; Al-Hayanni, Mohammed A. N.; Xia, Fei; Shafik, Rishad; Romanovsky, Alexander; Yakovlev, Alex (2018-07-01). "Speedup and Power Scaling Models for Heterogeneous Many-Core Systems". IEEE Transactions on Multi-Scale Computing Systems. 4 (3): 436–449. doi:10.1109/TMSCS.2018.2791531. ISSN 2332-7766. S2CID 52287374.
- Al-hayanni, Mohammed A. Noaman; Xia, Fei; Rafiev, Ashur; Romanovsky, Alexander; Shafik, Rishad; Yakovlev, Alex (July 2020). "Amdahl's law in the context of heterogeneous many-core systems – a survey". IET Computers & Digital Techniques. 14 (4): 133–148. doi:10.1049/iet-cdt.2018.5220. ISSN 1751-8601. S2CID 214415079.
Further reading
- Amdahl, Gene M. (1967). "Validity of the Single Processor Approach to Achieving Large-Scale Computing Capabilities" (PDF). AFIPS Conference Proceedings (30): 483–485. doi:10.1145/1465482.1465560. S2CID 195607370.
External links
- Gene M. Amdahl (1989), Oral history interview with Gene M. Amdahl, Charles Babbage Institute, University of Minnesota, hdl:11299/104341. Amdahl discusses his graduate work at the University of Wisconsin and his design of WISC. Discusses his role in the design of several computers for IBM including the STRETCH, IBM 701, and IBM 704. He discusses his work with Nathaniel Rochester and IBM's management of the design process. Mentions work with Ramo-Wooldridge, Aeronutronic, and Computer Sciences Corporation
- "Amdahl's Law" by Joel F. Klein, Wolfram Demonstrations Project (2007)
- Amdahl's Law in the Multicore Era (July 2008)
| Computer laws | |
|---|---|
| Semantically, a computer law is not a hard and fast law, but a rule of thumb, or axiom (postulation) |
| Parallel computing | |
|---|---|
| General | |
| Levels | |
| Multithreading | |
| Theory | |
| Elements | |
| Coordination | |
| Programming | |
| Hardware | |
| APIs | |
| Problems | |



 represents the total speedup of a program
represents the total speedup of a program represents time spent on the code where parallelism is used
represents time spent on the code where parallelism is used represents the extent of the improvement
represents the extent of the improvement . It includes the execution time of the part that would not benefit from the improvement of the resources and the execution time of the one that would benefit from it. The fraction of the execution time of the task that would benefit from the improvement of the resources is denoted by
. It includes the execution time of the part that would not benefit from the improvement of the resources and the execution time of the one that would benefit from it. The fraction of the execution time of the task that would benefit from the improvement of the resources is denoted by  . The one concerning the part that would not benefit from it is therefore
. The one concerning the part that would not benefit from it is therefore  . Then:
. Then:

 after the improvement of the resources. Consequently, the execution time of the part that does not benefit from it remains the same, while the part that benefits from it becomes:
after the improvement of the resources. Consequently, the execution time of the part that does not benefit from it remains the same, while the part that benefits from it becomes:

 of the whole task after the improvement of the resources is then:
of the whole task after the improvement of the resources is then:

 , which yields
, which yields






 , then
, then


 , we have
, we have  , meaning that the speedup is
measured with respect to the execution time after the non-parallelizable part is optimized.
, meaning that the speedup is
measured with respect to the execution time after the non-parallelizable part is optimized.
 ,
,

 ,
,  and
and  , then:
, then:

 , and the parallelizable part is correspondingly increased. Then
, and the parallelizable part is correspondingly increased. Then

