| Condensed matter experiments |
|---|

|
| ARPES |
| ACAR |
| Neutron scattering |
| X-ray spectroscopy |
| Quantum oscillations |
| Scanning tunneling microscopy |
Angular Correlation of Electron Positron Annihilation Radiation (ACAR or ACPAR) is a technique of solid state physics to investigate the electronic structure of metals. It uses positrons which are implanted into a sample and annihilate with the electrons. In the majority of annihilation events, two gamma quanta are created that are, in the reference frame of the electron-positron pair, emitted in exactly opposite directions. In the laboratory frame, there is a small angular deviation from collinearity, which is caused by the momentum of the electron. Hence, measuring the angular correlation of the annihilation radiation yields information about the momentum distribution of the electrons in the solid.
Investigation of the electronic structure

All the macroscopic electronic and magnetic properties of a solid result from its microscopic electronic structure. In the simple free electron model, the electrons do not interact with each other nor with the atomic cores. The relation between energy and momentum is given by
with the electron mass . Hence, there is an unambiguous connection between electron energy and momentum. Because of the Pauli exclusion principle the electrons fill all the states up to a maximum energy, the so-called Fermi energy. By the momentum-energy relation, this corresponds to the Fermi momentum . The border between occupied and unoccupied momentum states, the Fermi surface, is arguably the most significant feature of the electronic structure and has a strong influence on the solid's properties. In the free electron model, the Fermi surface is a sphere.
With ACAR it is possible to measure the momentum distribution of the electrons. A measurement on a free electron gas for example would give a positive intensity for momenta and zero intensity for . The Fermi surface itself can easily be identified from such a measurement by the discontinuity at .

In reality, there is interaction between the electrons with each other and the atomic cores of the crystal. This has several consequences: For example, the unambiguous relation between energy and momentum of an electronic state is broken and an electronic band structure is formed. Measuring the momentum of one electronic state gives a distribution of momenta which are all separated by reciprocal lattice vectors. Hence, an ACAR measurement on a solid with completely filled bands (i.e. on an insulator) gives a continuous distribution. An ACAR measurement on a metal has discontinuities where bands cross the Fermi level in all Brillouin zones in reciprocal space. This discontinuous distribution is superimposed by a continuous distribution from the entirely filled bands. From the discontinuities the Fermi surface can be extracted.
Since positrons that are created by beta decay possess a longitudinal spin polarization it is possible to investigate the spin-resolved electronic structure of magnetic materials. In this way, contributions from the majority and minority spin channel can be separated and the Fermi surface in the respective spin channels can be measured.
ACAR has several advantages and disadvantages compared to other, more well known techniques for the investigation of the electronic structure like ARPES and quantum oscillation: ACAR requires neither low temperatures, high magnetic fields or UHV conditions. Furthermore, it is possible to probe the electronic structure at the surface and in the bulk ( 100 nm deep). However, ACAR is reliant on defect free samples as vacancy concentrations of up to 10 per atom can efficiently trap positrons and distort the measurement.
Theory
In an ACAR measurement the angular deviation of many pairs of annihilation radiation is measured. Therefore, the underlying physical observable is often called 'two photon momentum density' (TPMD) or . Quantum mechanically, can be expressed as the squared absolute value of the Fourier transform of the multi-particle wave function of all the electron and the positron in the solid:
As it is not possible to imagine or compute the multi-particle wave function , it is often written as the sum of the single particle wave functions of the electron in the th state in the th band and the positron wave function :
The enhancement factor accounts for the electron-positron correlation. There exist sophisticated enhancement models to describe the electron-positron correlations, but in the following it will be assumed that . This approximation is called the independent particle model (IPM).
A very illustrative form of the TPMD can be obtained by the use of the Fourier coefficients for the wave function product :
These Fourier coefficients are distributed over all reciprocal vectors . If one assumes that the overlap of the electron and the positron wave function is constant for the same band , summing over all reciprocal lattice vectors gives a very instructive result:
The function is the Heaviside step function and the constant . This means, if is folded back into the first Brillouin zone, the resulting density is flat except at the Fermi momentum. Therefore, the Fermi surface can be easily identified by looking for this discontinuities in .
Experimental details
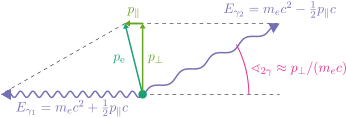
When a positron is implanted into a solid it will quickly lose all its kinetic energy and annihilate with an electron. By this process two gamma quanta with 511 keV each are created which are in the reference frame of the electron positron pair emitted in exactly anti-parallel directions. In the laboratory frame, however, there is a Doppler shift from 511 keV and an angular deviation from collinearity. Although the full momentum information about the momentum of the electron is encoded in the annihilation radiation, due to technical limitations it cannot be fully recovered. Either one measures the Doppler broadening of the 511 keV annihilation radiation (DBAR) or the angular correlation of the annihilation radiation (ACAR).
For DBAR a detector with a high energy resolution like a high purity germanium detector is needed. Such detectors typically do not resolve the position of absorbed photons. Hence only the longitudinal component of the electron momentum can be measured. The resulting measurement is a 1D projection of .
In ACAR position sensitive detectors, gamma cameras or multi wire proportional chambers, are used. Such detectors have a position resolution of typically 1 to 3 mm but an energy resolution which is just good enough to sort out scattered photons or background radiation. As is discarded, a 2D projection of is measured. In order to get a high angular resolution of 1×10 rad and better, the detectors have to be set up at distances between 16 and 20 m from each other. Although it is possible to get even better angular resolutions by placing the detectors further apart, this comes at cost of the counting rate. Already with moderate detector distances, the measurement of one projection of typically takes weeks.
As ACAR measures projections of the TPMD it is necessary to reconstruct in order to recover the Fermi surface. For such a reconstruction similar techniques as for X-ray computed tomography are used. In contrast to a human body, a crystal has many symmetries which can be included into the reconstruction. This makes the procedure more complex but increases the quality of the reconstruction. Another way to evaluate ACAR spectra is by a quantitative comparison with ab initio calculations.
History
In the early years, ACAR was mainly used to investigate the physics of the electron-positron annihilation process. In the 1930s several annihilation mechanism were discussed. Otto Klemperer could show with his angular correlation setup that the electron-positron pairs annihilate mainly into two gamma quanta which are emitted anti-parallel. In the 1950s, it was realized that by measuring the deviation from collinearity of the annihilation radiation information about the electronic structure of a solid can be obtained.
During this time mainly setups with 'long slit geometry' were used. They consisted of a positron source and a sample in the center, one fixed detector on one side and a second movable detector on the other side of the sample. Each detector was collimated in such a way that the active area was much smaller in one than in the other dimension (thus 'long slit'). A measurement with a long slit setup yields a 1D projection of the electron momentum density . Hence, this technique is called 1D-ACAR.
The development of two-dimensional gamma cameras and multi wire proportional chambers in the 1970s and early 1980s led to the setting up of the first 2D-ACAR spectrometer. This was an improvement to 1D-ACAR in two ways: i) The detection efficiency could be improved and ii) the informational content was greatly increased as the measurement gave a 2D projection of . An important early example of the use of spin-polarized 2D-ACAR is the proof of half metallicity in the half-Heusler alloy NiMnSb.
References
- Weber, J. A.; Böni, P.; Ceeh, H.; Leitner, M.; Hugenschmidt, Ch (2013-01-01). "First 2D-ACAR Measurements on Cu with the new Spectrometer at TUM". Journal of Physics: Conference Series. 443 (1): 012092. arXiv:1304.5363. Bibcode:2013JPhCS.443a2092W. doi:10.1088/1742-6596/443/1/012092. ISSN 1742-6596. S2CID 119246268.
- Dugdale, S. B. (2016-01-01). "Life on the edge: a beginner's guide to the Fermi surface". Physica Scripta. 91 (5): 053009. Bibcode:2016PhyS...91e3009D. doi:10.1088/0031-8949/91/5/053009. hdl:1983/18576e8a-c769-424d-8ac2-1c52ef80700e. ISSN 1402-4896.
- Weber, J. A. (2015-01-01). "Spin-Resolved Fermi Surface of the Localized Ferromagnetic Heusler Compound". Physical Review Letters. 115 (20): 206404. arXiv:1510.07808. Bibcode:2015PhRvL.115t6404W. doi:10.1103/PhysRevLett.115.206404. PMID 26613459. S2CID 29184856.
- Jarlborg, T.; Singh, A. K. (1987-01-09). "Local-density approach for calculation of electron-positron enhancement in transition metals". Phys. Rev. B. 36 (9): 4660–4663. Bibcode:1987PhRvB..36.4660J. doi:10.1103/PhysRevB.36.4660. PMID 9943477.
- Lock, D. G.; Crisp, V. H. C.; West, R. N. (1973-01-01). "Positron annihilation and Fermi surface studies: a new approach". Journal of Physics F: Metal Physics. 3 (3): 561. Bibcode:1973JPhF....3..561L. doi:10.1088/0305-4608/3/3/014. ISSN 0305-4608.
- Ceeh, Hubert; Weber, J. A.; Leitner, Michael; Böni, Peter; Hugenschmidt, Christoph (2013-04-01). "The source-sample stage of the new two-dimensional angular correlation of annihilation radiation spectrometer at Technische Universität München". Review of Scientific Instruments. 84 (4): 043905–043905–7. Bibcode:2013RScI...84d3905C. doi:10.1063/1.4801454. ISSN 0034-6748. PMID 23635207. S2CID 37765775.
- Ceeh, Hubert (2016-02-16). "Local electron-electron interaction strength in ferromagnetic nickel determined by spin-polarized positron annihilation". Scientific Reports. 6: 20898. arXiv:1501.02584. Bibcode:2016NatSR...620898C. doi:10.1038/srep20898. ISSN 2045-2322. PMC 4754699. PMID 26879249.
- Fermi, Enrico; Uhlenbeck, George (1933-01-01). "On the Recombination of Electrons and Positrons". Physical Review. 44 (6): 510–511. Bibcode:1933PhRv...44..510F. doi:10.1103/PhysRev.44.510.2. S2CID 14182018.
- ^ Klemperer, Otto (1934-07-01). "On the annihilation radiation of the positron". Mathematical Proceedings of the Cambridge Philosophical Society. 30 (3): 347–354. Bibcode:1934PCPS...30..347K. doi:10.1017/s0305004100012536. ISSN 1469-8064. S2CID 52101784.
- Perrin, F. (1933). "Materialisation d'electrons lors du choc de deuxelectrons. Processus divers d'annihilation deselectrons positifs". Comptes Rendus de l'Académie des Sciences. 197: 1302.
- DeBenedetti, S.; Cowan, C. E.; Konneker, W. R.; Primakoff, H. (1950-01-01). "On the Angular Distribution of Two-Photon Annihilation Radiation". Phys. Rev. 77 (2): 205. Bibcode:1950PhRv...77..205D. doi:10.1103/PhysRev.77.205.
- Maier-Leibnitz, Heinz (1951). "Impuls bei der Vernichtung langsamer Positronen in verschiedenen festen Stoffen". Zeitschrift für Naturforschung A. 6 (11): 663. Bibcode:1951ZNatA...6..663M. doi:10.1515/zna-1951-1117. S2CID 93760583.
- Fujiwara, Kunio; Sueoka, Osamu (1966-01-07). "A Precise Measurement of the Angular Correlation of Annihilation Radiation in Copper Single Crystals". Journal of the Physical Society of Japan. 21 (10): 1947. Bibcode:1966JPSJ...21.1947F. doi:10.1143/JPSJ.21.1947.
- Manuel, A. A.; Fischer, Ø.; Peter, M.; Jeavons, A. P. (1978-10-15). "An application of proportional chambers to the measurement of the electronic properties of solids by positron annihilation". Nuclear Instruments and Methods. 156 (1): 67–71. Bibcode:1978NucIM.156...67M. doi:10.1016/0029-554X(78)90693-6.
- West, R. N. (1981). "A high-efficiency two-dimensional angular correlation spectrometer for positron studies". Journal of Physics E: Scientific Instruments. 14 (4): 478–488. Bibcode:1981JPhE...14..478W. doi:10.1088/0022-3735/14/4/021.
- Hanssen, K. E. H. M.; Mijnarends, P. E. (1986-01-10). "Positron-annihilation study of the half-metallic ferromagnet NiMnSb: Theory". Phys. Rev. B. 34 (8): 5009–5016. Bibcode:1986PhRvB..34.5009H. doi:10.1103/PhysRevB.34.5009. PMID 9940323.
- Hanssen, K. E. H. M.; Mijnarends, P. E.; Rabou, L. P. L. M.; Buschow, K. H. J. (1990-01-07). "Positron-annihilation study of the half-metallic ferromagnet NiMnSb: Experiment". Phys. Rev. B. 42 (3): 1533–1540. Bibcode:1990PhRvB..42.1533H. doi:10.1103/PhysRevB.42.1533. PMID 9995582.
Notes
- This sensitivity is used in positron lifetime spectroscopy to investigate even very low defect concentrations.
- For simplicity the electron-electron correlation is ignored in this example.
- Further details about an ACAR setup can be found in
- For a sketch of a long slit setup see for example
Further reading
- Dupasquier, Alfredo (1995-01-01). Positron Spectroscopy of Solids. IOS Press. ISBN 9789051992038.
- Dugdale, S. B. (2014). "Probing the Fermi surface by positron annihilation and Compton scattering". Low Temperature Physics. 40 (4): 328. Bibcode:2014LTP....40..328D. doi:10.1063/1.4869588. hdl:1983/df44f2a9-b0e0-4900-8fb2-8a74d13a3889.
 and momentum
and momentum  is given by
is given by

 . Hence, there is an unambiguous connection between electron energy and momentum. Because of the
. Hence, there is an unambiguous connection between electron energy and momentum. Because of the  . The border between occupied and unoccupied momentum states, the
. The border between occupied and unoccupied momentum states, the  and zero intensity for
and zero intensity for  . The Fermi surface itself can easily be identified from such a measurement by the discontinuity at
. The Fermi surface itself can easily be identified from such a measurement by the discontinuity at  100
100  . Quantum mechanically,
. Quantum mechanically,  of all the electron and the positron in the solid:
of all the electron and the positron in the solid:

 in the
in the  th state in the
th state in the  th band and the positron wave function
th band and the positron wave function  :
:

 accounts for the electron-positron correlation. There exist sophisticated enhancement models to describe the electron-positron correlations, but in the following it will be assumed that
accounts for the electron-positron correlation. There exist sophisticated enhancement models to describe the electron-positron correlations, but in the following it will be assumed that  . This approximation is called the independent particle model (IPM).
. This approximation is called the independent particle model (IPM).
 :
:

 . If one assumes that the overlap of the electron and the positron wave function is constant for the same band
. If one assumes that the overlap of the electron and the positron wave function is constant for the same band 
 is the
is the  . This means, if
. This means, if  .
.
 can be measured. The resulting measurement is a 1D projection of
can be measured. The resulting measurement is a 1D projection of