Misplaced Pages

Bilunabirotunda
Type	Johnson J90 – J91 – J92
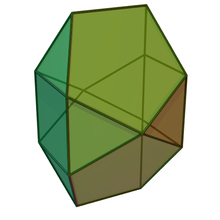
Faces	8 triangles 2 squares 4 pentagons
Edges	26
Vertices	14
Vertex configuration	4(3.5) 8(3.4.3.5) 2(3.5.3.5)
Symmetry group	${\displaystyle \mathrm {D} _{2\mathrm {h} }}$
Properties	convex, elementary
Net

In geometry, the bilunabirotunda is a Johnson solid with faces of 8 equilateral triangles, 2 squares, and 4 regular pentagons.

Properties

The bilunabirotunda is named from the prefix lune, meaning a figure featuring two triangles adjacent to opposite sides of a square. Therefore, the faces of a bilunabirotunda possess 8 equilateral triangles, 2 squares, and 4 regular pentagons as it faces. It is one of the Johnson solids—a convex polyhedron in which all of the faces are regular polygon—enumerated as 91st Johnson solid ${\displaystyle J_{91}}$. It is known as the elementary polyhedron, meaning that it cannot be separated by a plane into two small regular-faced polyhedra.

The surface area of a bilunabirotunda with edge length ${\displaystyle a}$ is: $${\displaystyle \left(2+2{\sqrt {3}}+{\sqrt {5(5+2{\sqrt {5}})}}\right)a^{2}\approx 12.346a^{2},}$$ and the volume of a bilunabirotunda is: $${\displaystyle {\frac {17+9{\sqrt {5}}}{12}}a^{3}\approx 3.0937a^{3}.}$$

Cartesian coordinates

One way to construct a bilunabirotunda with edge length ${\displaystyle {\sqrt {5}}-1}$ is by union of the orbits of the coordinates $${\displaystyle (0,0,1),\left({\frac {{\sqrt {5}}-1}{2}},1,{\frac {{\sqrt {5}}-1}{2}}\right),\left({\frac {{\sqrt {5}}-1}{2}},{\frac {{\sqrt {5}}+1}{2}}\right).}$$ under the group's action (of order 8) generated by reflections about coordinate planes.

Applications

Reynolds (2004) discusses the bilunabirotunda as a shape that could be used in architecture.

Related polyhedra and honeycombs

Six bilunabirotundae can be augmented around a cube with pyritohedral symmetry. B. M. Stewart labeled this six-bilunabirotunda model as 6J₉₁(P₄). Such clusters combine with regular dodecahedra to form a space-filling honeycomb.

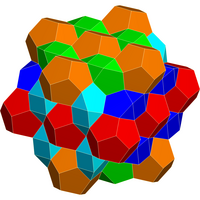Spacefilling honeycomb

6 bilunabirotundae around a cube

12 bilunabirotundae around a dodecahedron

References

1. ^ Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
2. Francis, D. (August 2013). "Johnson solids & their acronyms". Word Ways. 46 (3): 177.
3. Cromwell, P. R. (1997). Polyhedra. Cambridge University Press. p. 86–87, 89. ISBN 978-0-521-66405-9.
4. Timofeenko, A. V. (2009). "The Non-Platonic and Non-Archimedean Noncomposite Polyhedra". Journal of Mathematical Sciences. 162 (5): 710–729. doi:10.1007/s10958-009-9655-0.
5. Reynolds, M. A. (2004). "The Bilunabirotunda". Nexus Network Journal. 6: 43–47. doi:10.1007/s00004-004-0005-8.
6. B. M. Stewart, Adventures Among the Toroids: A Study of Quasi-Convex, Aplanar, Tunneled Orientable Polyhedra of Positive Genus Having Regular Faces With Disjoint Interiors (1980) ISBN 978-0686119364, (page 127, 2nd ed.) polyhedron 6J₉₁(P₄).

External links

• Weisstein, Eric W., "Bilunabirotunda" ("Johnson solid") at MathWorld.
• Miracle Spacefilling (Dodecahedron&Cube&Johnson solid No.91)

• Elementary polyhedron
• Johnson solids