| Rectified 24-cell | ||
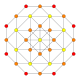
 Schlegel diagram 8 of 24 cuboctahedral cells shown | ||
| Type | Uniform 4-polytope | |
| Schläfli symbols | r{3,4,3} = rr{3,3,4}= r{3} = | |
| Coxeter diagrams | ||
| Cells | 48 | 24 3.4.3.4 24 4.4.4 |
| Faces | 240 | 96 {3} 144 {4} |
| Edges | 288 | |
| Vertices | 96 | |
| Vertex figure |    Triangular prism | |
| Symmetry groups | F4 , order 1152 B4 , order 384 D4 , order 192 | |
| Properties | convex, edge-transitive | |
| Uniform index | 22 23 24 | |

In geometry, the rectified 24-cell or rectified icositetrachoron is a uniform 4-dimensional polytope (or uniform 4-polytope), which is bounded by 48 cells: 24 cubes, and 24 cuboctahedra. It can be obtained by rectification of the 24-cell, reducing its octahedral cells to cubes and cuboctahedra.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC24.
It can also be considered a cantellated 16-cell with the lower symmetries B4 = . B4 would lead to a bicoloring of the cuboctahedral cells into 8 and 16 each. It is also called a runcicantellated demitesseract in a D4 symmetry, giving 3 colors of cells, 8 for each.
Construction
The rectified 24-cell can be derived from the 24-cell by the process of rectification: the 24-cell is truncated at the midpoints. The vertices become cubes, while the octahedra become cuboctahedra.
Cartesian coordinates
A rectified 24-cell having an edge length of √2 has vertices given by all permutations and sign permutations of the following Cartesian coordinates:
- (0,1,1,2)
The dual configuration with edge length 2 has all coordinate and sign permutations of:
- (0,2,2,2)
- (1,1,1,3)
Images
| Coxeter plane | F4 | |
|---|---|---|
| Graph | 
| |
| Dihedral symmetry | ||
| Coxeter plane | B3 / A2 (a) | B3 / A2 (b) |
| Graph | 
|
|
| Dihedral symmetry | ||
| Coxeter plane | B4 | B2 / A3 |
| Graph | 
|

|
| Dihedral symmetry | ||
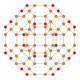
| Stereographic projection | |
|---|---|
 | |
| Center of stereographic projection with 96 triangular faces blue | |
Symmetry constructions
There are three different symmetry constructions of this polytope. The lowest construction can be doubled into by adding a mirror that maps the bifurcating nodes onto each other. can be mapped up to symmetry by adding two mirror that map all three end nodes together.
The vertex figure is a triangular prism, containing two cubes and three cuboctahedra. The three symmetries can be seen with 3 colored cuboctahedra in the lowest construction, and two colors (1:2 ratio) in , and all identical cuboctahedra in .
| Coxeter group | = | = | = |
|---|---|---|---|
| Order | 1152 | 384 | 192 |
| Full symmetry group |
<> = ] = | ||
| Coxeter diagram | |||
| Facets | 3: 2: |
2,2: 2: |
1,1,1: 2: |
| Vertex figure | 
|

|

|
Alternate names
- Rectified 24-cell, Cantellated 16-cell (Norman Johnson)
- Rectified icositetrachoron (Acronym rico) (George Olshevsky, Jonathan Bowers)
- Cantellated hexadecachoron
- Disicositetrachoron
- Amboicositetrachoron (Neil Sloane & John Horton Conway)
Related polytopes
The convex hull of the rectified 24-cell and its dual (assuming that they are congruent) is a nonuniform polychoron composed of 192 cells: 48 cubes, 144 square antiprisms, and 192 vertices. Its vertex figure is a triangular bifrustum.
Related uniform polytopes
| D4 uniform polychora | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|

|
|

|

|

|
|
| ||||
| {3,3} h{4,3,3} |
2r{3,3} h3{4,3,3} |
t{3,3} h2{4,3,3} |
2t{3,3} h2,3{4,3,3} |
r{3,3} {3}={3,4,3} |
rr{3,3} r{3}=r{3,4,3} |
tr{3,3} t{3}=t{3,4,3} |
sr{3,3} s{3}=s{3,4,3} | ||||
| 24-cell family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | 24-cell | truncated 24-cell | snub 24-cell | rectified 24-cell | cantellated 24-cell | bitruncated 24-cell | cantitruncated 24-cell | runcinated 24-cell | runcitruncated 24-cell | omnitruncated 24-cell | |
| Schläfli symbol |
{3,4,3} | t0,1{3,4,3} t{3,4,3} |
s{3,4,3} | t1{3,4,3} r{3,4,3} |
t0,2{3,4,3} rr{3,4,3} |
t1,2{3,4,3} 2t{3,4,3} |
t0,1,2{3,4,3} tr{3,4,3} |
t0,3{3,4,3} | t0,1,3{3,4,3} | t0,1,2,3{3,4,3} | |
| Coxeter diagram |
|||||||||||
| Schlegel diagram |

|

|

|

|

|

|

|

|

|

| |
| F4 | 
|

|

|

|

|

|

|

|

|

| |
| B4 | 
|

|

|

|
|

|

|

|

|

| |
| B3(a) | 
|

|

|

|

|

|

|

|
|

| |
| B3(b) | 
|

|

|
|

|
| |||||
| B2 | 
|

|

|

|

|

|

|
|
|

| |
The rectified 24-cell can also be derived as a cantellated 16-cell:
| B4 symmetry polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | tesseract | rectified tesseract |
truncated tesseract |
cantellated tesseract |
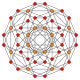
runcinated tesseract |
bitruncated tesseract |
cantitruncated tesseract |
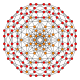
runcitruncated tesseract |
omnitruncated tesseract | ||
| Coxeter diagram |
= |
= |
|||||||||
| Schläfli symbol |
{4,3,3} | t1{4,3,3} r{4,3,3} |
t0,1{4,3,3} t{4,3,3} |
t0,2{4,3,3} rr{4,3,3} |
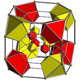
t0,3{4,3,3} | t1,2{4,3,3} 2t{4,3,3} |
t0,1,2{4,3,3} tr{4,3,3} |
t0,1,3{4,3,3} | t0,1,2,3{4,3,3} | ||
| Schlegel diagram |

|

|
|

|

|

|
|
|

| ||
| B4 | 
|

|

|

|
|

|

|
|

| ||
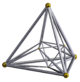
| Name | 16-cell | rectified 16-cell |
truncated 16-cell |
cantellated 16-cell |
runcinated 16-cell |
bitruncated 16-cell |
cantitruncated 16-cell |
runcitruncated 16-cell |
omnitruncated 16-cell | ||
| Coxeter diagram |
= |
= |
= |
= |
= |
= |
|||||
| Schläfli symbol |
{3,3,4} | t1{3,3,4} r{3,3,4} |
t0,1{3,3,4} t{3,3,4} |
t0,2{3,3,4} rr{3,3,4} |
t0,3{3,3,4} | t1,2{3,3,4} 2t{3,3,4} |
t0,1,2{3,3,4} tr{3,3,4} |
t0,1,3{3,3,4} | t0,1,2,3{3,3,4} | ||
| Schlegel diagram |
|

|

|

|

|
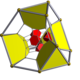
|

|
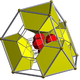
|

| ||
| B4 | 
|

|

|

|

|

|

|

|

| ||
Citations
- Coxeter 1973, p. 154, §8.4.
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- Coxeter, H.S.M. (1973) . Regular Polytopes (3rd ed.). New York: Dover.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Model 23, George Olshevsky.
- 3. Convex uniform polychora based on the icositetrachoron (24-cell) - Model 23, George Olshevsky.
- 7. Uniform polychora derived from glomeric tetrahedron B4 - Model 23, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) o3x4o3o - rico".
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||



 construction can be doubled into
construction can be doubled into  by adding a mirror that maps the bifurcating nodes onto each other.
by adding a mirror that maps the bifurcating nodes onto each other.  symmetry by adding two mirror that map all three end nodes together.
symmetry by adding two mirror that map all three end nodes together.