
A covalent bond is a chemical bond that involves the sharing of electrons to form electron pairs between atoms. These electron pairs are known as shared pairs or bonding pairs. The stable balance of attractive and repulsive forces between atoms, when they share electrons, is known as covalent bonding. For many molecules, the sharing of electrons allows each atom to attain the equivalent of a full valence shell, corresponding to a stable electronic configuration. In organic chemistry, covalent bonding is much more common than ionic bonding.
Covalent bonding also includes many kinds of interactions, including σ-bonding, π-bonding, metal-to-metal bonding, agostic interactions, bent bonds, three-center two-electron bonds and three-center four-electron bonds. The term covalent bond dates from 1939. The prefix co- means jointly, associated in action, partnered to a lesser degree, etc.; thus a "co-valent bond", in essence, means that the atoms share "valence", such as is discussed in valence bond theory.
In the molecule H
2, the hydrogen atoms share the two electrons via covalent bonding. Covalency is greatest between atoms of similar electronegativities. Thus, covalent bonding does not necessarily require that the two atoms be of the same elements, only that they be of comparable electronegativity. Covalent bonding that entails the sharing of electrons over more than two atoms is said to be delocalized.
History

The term covalence in regard to bonding was first used in 1919 by Irving Langmuir in a Journal of the American Chemical Society article entitled "The Arrangement of Electrons in Atoms and Molecules". Langmuir wrote that "we shall denote by the term covalence the number of pairs of electrons that a given atom shares with its neighbors."
The idea of covalent bonding can be traced several years before 1919 to Gilbert N. Lewis, who in 1916 described the sharing of electron pairs between atoms (and in 1926 he also coined the term "photon" for the smallest unit of radiant energy). He introduced the Lewis notation or electron dot notation or Lewis dot structure, in which valence electrons (those in the outer shell) are represented as dots around the atomic symbols. Pairs of electrons located between atoms represent covalent bonds. Multiple pairs represent multiple bonds, such as double bonds and triple bonds. An alternative form of representation, not shown here, has bond-forming electron pairs represented as solid lines.
Lewis proposed that an atom forms enough covalent bonds to form a full (or closed) outer electron shell. In the diagram of methane shown here, the carbon atom has a valence of four and is, therefore, surrounded by eight electrons (the octet rule), four from the carbon itself and four from the hydrogens bonded to it. Each hydrogen has a valence of one and is surrounded by two electrons (a duet rule) – its own one electron plus one from the carbon. The numbers of electrons correspond to full shells in the quantum theory of the atom; the outer shell of a carbon atom is the n = 2 shell, which can hold eight electrons, whereas the outer (and only) shell of a hydrogen atom is the n = 1 shell, which can hold only two.
While the idea of shared electron pairs provides an effective qualitative picture of covalent bonding, quantum mechanics is needed to understand the nature of these bonds and predict the structures and properties of simple molecules. Walter Heitler and Fritz London are credited with the first successful quantum mechanical explanation of a chemical bond (molecular hydrogen) in 1927. Their work was based on the valence bond model, which assumes that a chemical bond is formed when there is good overlap between the atomic orbitals of participating atoms.
Types of covalent bonds
Atomic orbitals (except for s orbitals) have specific directional properties leading to different types of covalent bonds. Sigma (σ) bonds are the strongest covalent bonds and are due to head-on overlapping of orbitals on two different atoms. A single bond is usually a σ bond. Pi (π) bonds are weaker and are due to lateral overlap between p (or d) orbitals. A double bond between two given atoms consists of one σ and one π bond, and a triple bond is one σ and two π bonds.
Covalent bonds are also affected by the electronegativity of the connected atoms which determines the chemical polarity of the bond. Two atoms with equal electronegativity will make nonpolar covalent bonds such as H–H. An unequal relationship creates a polar covalent bond such as with H−Cl. However polarity also requires geometric asymmetry, or else dipoles may cancel out, resulting in a non-polar molecule.
Covalent structures
There are several types of structures for covalent substances, including individual molecules, molecular structures, macromolecular structures and giant covalent structures. Individual molecules have strong bonds that hold the atoms together, but generally, there are negligible forces of attraction between molecules. Such covalent substances are usually gases, for example, HCl, SO2, CO2, and CH4. In molecular structures, there are weak forces of attraction. Such covalent substances are low-boiling-temperature liquids (such as ethanol), and low-melting-temperature solids (such as iodine and solid CO2). Macromolecular structures have large numbers of atoms linked by covalent bonds in chains, including synthetic polymers such as polyethylene and nylon, and biopolymers such as proteins and starch. Network covalent structures (or giant covalent structures) contain large numbers of atoms linked in sheets (such as graphite), or 3-dimensional structures (such as diamond and quartz). These substances have high melting and boiling points, are frequently brittle, and tend to have high electrical resistivity. Elements that have high electronegativity, and the ability to form three or four electron pair bonds, often form such large macromolecular structures.
One- and three-electron bonds

Bonds with one or three electrons can be found in radical species, which have an odd number of electrons. The simplest example of a 1-electron bond is found in the dihydrogen cation, H
2. One-electron bonds often have about half the bond energy of a 2-electron bond, and are therefore called "half bonds". However, there are exceptions: in the case of dilithium, the bond is actually stronger for the 1-electron Li
2 than for the 2-electron Li2. This exception can be explained in terms of hybridization and inner-shell effects.
The simplest example of three-electron bonding can be found in the helium dimer cation, He
2. It is considered a "half bond" because it consists of only one shared electron (rather than two); in molecular orbital terms, the third electron is in an anti-bonding orbital which cancels out half of the bond formed by the other two electrons. Another example of a molecule containing a 3-electron bond, in addition to two 2-electron bonds, is nitric oxide, NO. The oxygen molecule, O2 can also be regarded as having two 3-electron bonds and one 2-electron bond, which accounts for its paramagnetism and its formal bond order of 2. Chlorine dioxide and its heavier analogues bromine dioxide and iodine dioxide also contain three-electron bonds.
Molecules with odd-electron bonds are usually highly reactive. These types of bond are only stable between atoms with similar electronegativities.
Modified Lewis structures with 3e bonds Nitric oxide
Nitric oxide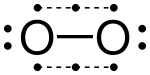 Dioxygen
Dioxygen
Resonance
Main article: Resonance (chemistry)There are situations whereby a single Lewis structure is insufficient to explain the electron configuration in a molecule and its resulting experimentally-determined properties, hence a superposition of structures is needed. The same two atoms in such molecules can be bonded differently in different Lewis structures (a single bond in one, a double bond in another, or even none at all), resulting in a non-integer bond order. The nitrate ion is one such example with three equivalent structures. The bond between the nitrogen and each oxygen is a double bond in one structure and a single bond in the other two, so that the average bond order for each N–O interaction is 2 + 1 + 1/3 = 4/3.
Aromaticity
Main article: AromaticityIn organic chemistry, when a molecule with a planar ring obeys Hückel's rule, where the number of π electrons fit the formula 4n + 2 (where n is an integer), it attains extra stability and symmetry. In benzene, the prototypical aromatic compound, there are 6 π bonding electrons (n = 1, 4n + 2 = 6). These occupy three delocalized π molecular orbitals (molecular orbital theory) or form conjugate π bonds in two resonance structures that linearly combine (valence bond theory), creating a regular hexagon exhibiting a greater stabilization than the hypothetical 1,3,5-cyclohexatriene.
In the case of heterocyclic aromatics and substituted benzenes, the electronegativity differences between different parts of the ring may dominate the chemical behavior of aromatic ring bonds, which otherwise are equivalent.
Hypervalence
Main article: Hypervalent moleculeCertain molecules such as xenon difluoride and sulfur hexafluoride have higher coordination numbers than would be possible due to strictly covalent bonding according to the octet rule. This is explained by the three-center four-electron bond ("3c–4e") model which interprets the molecular wavefunction in terms of non-bonding highest occupied molecular orbitals in molecular orbital theory and resonance of sigma bonds in valence bond theory.
Electron deficiency
Main article: Electron deficiencyIn three-center two-electron bonds ("3c–2e") three atoms share two electrons in bonding. This type of bonding occurs in boron hydrides such as diborane (B2H6), which are often described as electron deficient because there are not enough valence electrons to form localized (2-centre 2-electron) bonds joining all the atoms. However, the more modern description using 3c–2e bonds does provide enough bonding orbitals to connect all the atoms so that the molecules can instead be classified as electron-precise.
Each such bond (2 per molecule in diborane) contains a pair of electrons which connect the boron atoms to each other in a banana shape, with a proton (the nucleus of a hydrogen atom) in the middle of the bond, sharing electrons with both boron atoms. In certain cluster compounds, so-called four-center two-electron bonds also have been postulated.
Quantum mechanical description
After the development of quantum mechanics, two basic theories were proposed to provide a quantum description of chemical bonding: valence bond (VB) theory and molecular orbital (MO) theory. A more recent quantum description is given in terms of atomic contributions to the electronic density of states.
Comparison of VB and MO theories
The two theories represent two ways to build up the electron configuration of the molecule. For valence bond theory, the atomic hybrid orbitals are filled with electrons first to produce a fully bonded valence configuration, followed by performing a linear combination of contributing structures (resonance) if there are several of them. In contrast, for molecular orbital theory, a linear combination of atomic orbitals is performed first, followed by filling of the resulting molecular orbitals with electrons.
The two approaches are regarded as complementary, and each provides its own insights into the problem of chemical bonding. As valence bond theory builds the molecular wavefunction out of localized bonds, it is more suited for the calculation of bond energies and the understanding of reaction mechanisms. As molecular orbital theory builds the molecular wavefunction out of delocalized orbitals, it is more suited for the calculation of ionization energies and the understanding of spectral absorption bands.
At the qualitative level, both theories contain incorrect predictions. Simple (Heitler–London) valence bond theory correctly predicts the dissociation of homonuclear diatomic molecules into separate atoms, while simple (Hartree–Fock) molecular orbital theory incorrectly predicts dissociation into a mixture of atoms and ions. On the other hand, simple molecular orbital theory correctly predicts Hückel's rule of aromaticity, while simple valence bond theory incorrectly predicts that cyclobutadiene has larger resonance energy than benzene.
Although the wavefunctions generated by both theories at the qualitative level do not agree and do not match the stabilization energy by experiment, they can be corrected by configuration interaction. This is done by combining the valence bond covalent function with the functions describing all possible ionic structures or by combining the molecular orbital ground state function with the functions describing all possible excited states using unoccupied orbitals. It can then be seen that the simple molecular orbital approach overestimates the weight of the ionic structures while the simple valence bond approach neglects them. This can also be described as saying that the simple molecular orbital approach neglects electron correlation while the simple valence bond approach overestimates it.
Modern calculations in quantum chemistry usually start from (but ultimately go far beyond) a molecular orbital rather than a valence bond approach, not because of any intrinsic superiority in the former but rather because the MO approach is more readily adapted to numerical computations. Molecular orbitals are orthogonal, which significantly increases the feasibility and speed of computer calculations compared to nonorthogonal valence bond orbitals.
Covalency from atomic contribution to the electronic density of states
Evaluation of bond covalency is dependent on the basis set for approximate quantum-chemical methods such as COOP (crystal orbital overlap population), COHP (Crystal orbital Hamilton population), and BCOOP (Balanced crystal orbital overlap population). To overcome this issue, an alternative formulation of the bond covalency can be provided in this way.
The mass center of an atomic orbital with quantum numbers for atom A is defined as
where is the contribution of the atomic orbital of the atom A to the total electronic density of states of the solid
where the outer sum runs over all atoms A of the unit cell. The energy window is chosen in such a way that it encompasses all of the relevant bands participating in the bond. If the range to select is unclear, it can be identified in practice by examining the molecular orbitals that describe the electron density along with the considered bond.
The relative position of the mass center of levels of atom A with respect to the mass center of levels of atom B is given as
where the contributions of the magnetic and spin quantum numbers are summed. According to this definition, the relative position of the A levels with respect to the B levels is
where, for simplicity, we may omit the dependence from the principal quantum number in the notation referring to
In this formalism, the greater the value of the higher the overlap of the selected atomic bands, and thus the electron density described by those orbitals gives a more covalent A−B bond. The quantity is denoted as the covalency of the A−B bond, which is specified in the same units of the energy .
Analogous effect in nuclear systems
An analogous effect to covalent binding is believed to occur in some nuclear systems, with the difference that the shared fermions are quarks rather than electrons. High energy proton-proton scattering cross-section indicates that quark interchange of either u or d quarks is the dominant process of the nuclear force at short distance. In particular, it dominates over the Yukawa interaction where a meson is exchanged. Therefore, covalent binding by quark interchange is expected to be the dominating mechanism of nuclear binding at small distance when the bound hadrons have covalence quarks in common.
See also
- Bonding in solids
- Bond order
- Coordinate covalent bond, also known as a dipolar bond or a dative covalent bond
- Covalent bond classification (or LXZ notation)
- Covalent radius
- Disulfide bond
- Hybridization
- Hydrogen bond
- Ionic bond
- Linear combination of atomic orbitals
- Metallic bonding
- Noncovalent bonding
- Resonance (chemistry)
References
- Whitten, Kenneth W.; Gailey, Kenneth D.; Davis, Raymond E. (1992). "7-3 Formation of covalent bonds". General Chemistry (4th ed.). Saunders College Publishing. p. 264. ISBN 0-03-072373-6.
- March, Jerry (1992). Advanced Organic Chemistry: Reactions, Mechanisms, and Structure. John Wiley & Sons. ISBN 0-471-60180-2.
- Gary L. Miessler; Donald Arthur Tarr (2004). Inorganic Chemistry. Prentice Hall. ISBN 0-13-035471-6.
- Merriam-Webster – Collegiate Dictionary (2000).
- "Chemical Bonds". Hyperphysics.phy-astr.gsu.edu. Retrieved 2013-06-09.
- Langmuir, Irving (1919-06-01). "The Arrangement of Electrons in Atoms and Molecules". Journal of the American Chemical Society. 41 (6): 868–934. doi:10.1021/ja02227a002.
- Lewis, Gilbert N. (1916-04-01). "The atom and the molecule". Journal of the American Chemical Society. 38 (4): 762–785. doi:10.1021/ja02261a002. S2CID 95865413.
- ^ McMurry, John (2016). Chemistry (7 ed.). Pearson. ISBN 978-0-321-94317-0.
- ^ Bruice, Paula (2016). Organic Chemistry (8 ed.). Pearson. ISBN 978-0-13-404228-2.
- Heitler, W.; London, F. (1927). "Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik" [Interaction of neutral atoms and homeopolar bonds according to quantum mechanics]. Zeitschrift für Physik. 44 (6–7): 455–472. Bibcode:1927ZPhy...44..455H. doi:10.1007/bf01397394. S2CID 119739102. English translation in Hettema, H. (2000). Quantum Chemistry: Classic Scientific Papers. World Scientific. p. 140. ISBN 978-981-02-2771-5. Retrieved 2012-02-05.
- Stranks, D. R.; Heffernan, M. L.; Lee Dow, K. C.; McTigue, P. T.; Withers, G. R. A. (1970). Chemistry: A structural view. Carlton, Vic.: Melbourne University Press. p. 184. ISBN 0-522-83988-6.
- Weinhold, F.; Landis, C. (2005). Valency and Bonding. Cambridge. pp. 96–100. ISBN 0-521-83128-8.
- Harcourt, Richard D., ed. (2015). "Chapter 2: Pauling "3-Electron Bonds", 4-Electron 3-Centre Bonding, and the Need for an "Increased-Valence" Theory". Bonding in Electron-Rich Molecules: Qualitative Valence-Bond Approach via Increased-Valence Structures. Springer. ISBN 9783319166766.
- ^ Pauling, L. (1960). The Nature of the Chemical Bond. Cornell University Press. pp. 340–354.
- Weinhold, F.; Landis, C. (2005). Valency and Bonding. Cambridge University Press. pp. 275–306. ISBN 0521831288.
- Hofmann, K.; Prosenc, M. H.; Albert, B. R. (2007). "A new 4c–2e bond in B
6H
7". Chemical Communications. 2007 (29): 3097–3099. doi:10.1039/b704944g. PMID 17639154. - Cammarata, Antonio; Rondinelli, James M. (21 September 2014). "Covalent dependence of octahedral rotations in orthorhombic perovskite oxides". Journal of Chemical Physics. 141 (11): 114704. Bibcode:2014JChPh.141k4704C. doi:10.1063/1.4895967. PMID 25240365.
- ^ Atkins, P. W. (1974). Quanta: A Handbook of Concepts. Oxford University Press. pp. 147–148. ISBN 978-0-19-855493-6.
- James D. Ingle Jr. and Stanley R. Crouch, Spectrochemical Analysis, Prentice Hall, 1988, ISBN 0-13-826876-2
- Anslyn, Eric V. (2006). Modern Physical Organic Chemistry. University Science Books. ISBN 978-1-891389-31-3.
- Hughbanks, Timothy; Hoffmann, Roald (2002-05-01). "Chains of trans-edge-sharing molybdenum octahedra: metal-metal bonding in extended systems". Journal of the American Chemical Society. 105 (11): 3528–3537. doi:10.1021/ja00349a027.
- Dronskowski, Richard; Bloechl, Peter E. (2002-05-01). "Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations". The Journal of Physical Chemistry. 97 (33): 8617–8624. doi:10.1021/j100135a014.
- Grechnev, Alexei; Ahuja, Rajeev; Eriksson, Olle (2003-01-01). "Balanced crystal orbital overlap population—a tool for analysing chemical bonds in solids". Journal of Physics: Condensed Matter. 15 (45): 7751. Bibcode:2003JPCM...15.7751G. doi:10.1088/0953-8984/15/45/014. ISSN 0953-8984. S2CID 250757642.
- Brodsky, S. J. (2017). "Novel Features of Nuclear Chromodynamics". The European Physical Journal A. 53 (3): 48. Bibcode:2017EPJA...53...48B. doi:10.1140/epja/i2017-12234-5. OSTI 1341388. S2CID 126305939.
- Brodsky, S. J.; Mueller, A. H. (1988). "Using Nuclei to Probe Hadronization in QCD". Physics Letters B. 206 (4): 685. Bibcode:1988PhLB..206..685B. doi:10.1016/0370-2693(88)90719-8. OSTI 1448604.
- Bashkanova, M.; Brodsky, S. J.; Clement, H. (2013). "Novel Six-Quark Hidden-Color Dibaryon States in QCD". Physics Letters B. 727 (4–5): 438. arXiv:1308.6404. Bibcode:2013PhLB..727..438B. doi:10.1016/j.physletb.2013.10.059. S2CID 30153514.
Sources
- "Covalent bonding – Single bonds". chemguide. 2000. Retrieved 2012-02-05.
- "Electron Sharing and Covalent Bonds". Department of Chemistry University of Oxford. Retrieved 2012-02-05.
- "Chemical Bonds". Department of Physics and Astronomy, Georgia State University. Retrieved 2012-02-05.
External links
- Covalent Bonds and Molecular Structure Archived 2009-02-10 at the Wayback Machine
- Structure and Bonding in Chemistry—Covalent Bonds
| Chemical bonds | ||||||||
|---|---|---|---|---|---|---|---|---|
| Intramolecular (strong) |
|    | ||||||
| Intermolecular (weak) |
| |||||||
| Bond cleavage | ||||||||
| Electron counting rules | ||||||||
| Chemical bonding theory | |||||||
|---|---|---|---|---|---|---|---|
| Types of bonds |
| ||||||
| Valence bond theory |
| ||||||
| Molecular orbital theory |
| ||||||
| Concepts in organic chemistry | |
|---|---|

 of an atomic orbital
of an atomic orbital  with
with 


 for atom A is defined as
for atom A is defined as

 is the contribution of the atomic orbital
is the contribution of the atomic orbital  of the atom A to the total electronic density of states
of the atom A to the total electronic density of states  of the solid
of the solid

 is chosen in such a way that it encompasses all of the relevant bands participating in the bond. If the range to select is unclear, it can be identified in practice by examining the molecular orbitals that describe the electron density along with the considered bond.
is chosen in such a way that it encompasses all of the relevant bands participating in the bond. If the range to select is unclear, it can be identified in practice by examining the molecular orbitals that describe the electron density along with the considered bond.
 of the mass center of
of the mass center of  levels of atom A with respect to the mass center of
levels of atom A with respect to the mass center of  levels of atom B is given as
levels of atom B is given as


 in the notation referring to
in the notation referring to 
 the higher the overlap of the selected atomic bands, and thus the electron density described by those orbitals gives a more covalent A−B bond. The quantity
the higher the overlap of the selected atomic bands, and thus the electron density described by those orbitals gives a more covalent A−B bond. The quantity  is denoted as the covalency of the A−B bond, which is specified in the same units of the energy
is denoted as the covalency of the A−B bond, which is specified in the same units of the energy  .
.