The fixed end moments are reaction moments developed in a beam member under certain load conditions with both ends fixed. A beam with both ends fixed is statically indeterminate to the 3rd degree, and any structural analysis method applicable on statically indeterminate beams can be used to calculate the fixed end moments.
Examples
In the following examples, clockwise moments are positive.
 Concentrated load of magnitude P |
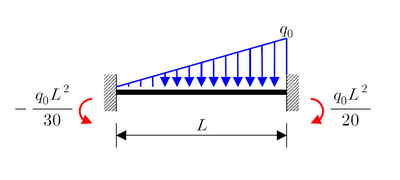 Linearly distributed load of maximum intensity q0 |
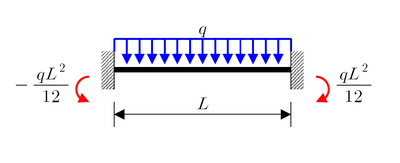 Uniformly distributed load of intensity q |
 Couple of magnitude M0 |
The two cases with distributed loads can be derived from the case with concentrated load by integration. For example, when a uniformly distributed load of intensity is acting on a beam, then an infinitely small part distance apart from the left end of this beam can be seen as being under a concentrated load of magnitude . Then,
Where the expressions within the integrals on the right hand sides are the fixed end moments caused by the concentrated load .
For the case with linearly distributed load of maximum intensity ,
See also
References
- Yang, Chang-hyeon (2001-01-10). Structural Analysis (in Korean) (4th ed.). Seoul: Cheong Moon Gak Publishers. ISBN 89-7088-709-1. Archived from the original on 2007-10-08. Retrieved 2007-09-03.
This article about a civil engineering topic is a stub. You can help Misplaced Pages by expanding it. |
 is acting on a beam, then an infinitely small part
is acting on a beam, then an infinitely small part  distance
distance  apart from the left end of this beam can be seen as being under a concentrated load of magnitude
apart from the left end of this beam can be seen as being under a concentrated load of magnitude  . Then,
. Then,


 ,
,

