| Algebraic structure → Group theory Group theory | ||||||
|---|---|---|---|---|---|---|
 | ||||||
Basic notions
|
||||||
Finite groups
|
||||||
Modular groups
|
||||||
Topological and Lie groups
|
||||||
| Algebraic groups | ||||||
In mathematics, given two groups, (G,∗) and (H, ·), a group homomorphism from (G,∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that
where the group operation on the left side of the equation is that of G and on the right side that of H.
From this property, one can deduce that h maps the identity element eG of G to the identity element eH of H,
and it also maps inverses to inverses in the sense that
Hence one can say that h "is compatible with the group structure".
In areas of mathematics where one considers groups endowed with additional structure, a homomorphism sometimes means a map which respects not only the group structure (as above) but also the extra structure. For example, a homomorphism of topological groups is often required to be continuous.
Properties
Let be the identity element of the (H, ·) group and , then
Now by multiplying for the inverse of (or applying the cancellation rule) we obtain
Similarly,
Therefore for the uniqueness of the inverse: .
Types
- Monomorphism
- A group homomorphism that is injective (or, one-to-one); i.e., preserves distinctness.
- Epimorphism
- A group homomorphism that is surjective (or, onto); i.e., reaches every point in the codomain.
- Isomorphism
- A group homomorphism that is bijective; i.e., injective and surjective. Its inverse is also a group homomorphism. In this case, the groups G and H are called isomorphic; they differ only in the notation of their elements (except of identity element) and are identical for all practical purposes. I.e. we re-label all elements except identity.
- Endomorphism
- A group homomorphism, h: G → G; the domain and codomain are the same. Also called an endomorphism of G.
- Automorphism
- A group endomorphism that is bijective, and hence an isomorphism. The set of all automorphisms of a group G, with functional composition as operation, itself forms a group, the automorphism group of G. It is denoted by Aut(G). As an example, the automorphism group of (Z, +) contains only two elements, the identity transformation and multiplication with −1; it is isomorphic to (Z/2Z, +).
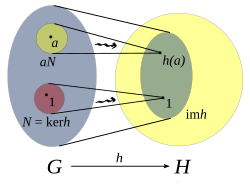
Image and kernel
Main articles: Image (mathematics) and kernel (algebra)We define the kernel of h to be the set of elements in G which are mapped to the identity in H
and the image of h to be
The kernel and image of a homomorphism can be interpreted as measuring how close it is to being an isomorphism. The first isomorphism theorem states that the image of a group homomorphism, h(G) is isomorphic to the quotient group G/ker h.
The kernel of h is a normal subgroup of G. Assume and show for arbitrary :
The image of h is a subgroup of H.
The homomorphism, h, is a group monomorphism; i.e., h is injective (one-to-one) if and only if ker(h) = {eG}. Injection directly gives that there is a unique element in the kernel, and, conversely, a unique element in the kernel gives injection:
Examples
- Consider the cyclic group Z3 = (Z/3Z, +) = ({0, 1, 2}, +) and the group of integers (Z, +). The map h : Z → Z/3Z with h(u) = u mod 3 is a group homomorphism. It is surjective and its kernel consists of all integers which are divisible by 3.
- The set
forms a group under matrix multiplication. For any complex number u the function fu : G → C defined by
- Consider a multiplicative group of positive real numbers (R, ⋅) for any complex number u. Then the function fu : R → C defined by
- The exponential map yields a group homomorphism from the group of real numbers R with addition to the group of non-zero real numbers R* with multiplication. The kernel is {0} and the image consists of the positive real numbers.
- The exponential map also yields a group homomorphism from the group of complex numbers C with addition to the group of non-zero complex numbers C* with multiplication. This map is surjective and has the kernel {2πki : k ∈ Z}, as can be seen from Euler's formula. Fields like R and C that have homomorphisms from their additive group to their multiplicative group are thus called exponential fields.
- The function , defined by is a homomorphism.
- Consider the two groups and , represented respectively by and , where is the positive real numbers. Then, the function defined by the logarithm function is a homomorphism.
Category of groups
If h : G → H and k : H → K are group homomorphisms, then so is k ∘ h : G → K. This shows that the class of all groups, together with group homomorphisms as morphisms, forms a category (specifically the category of groups).
Homomorphisms of abelian groups
If G and H are abelian (i.e., commutative) groups, then the set Hom(G, H) of all group homomorphisms from G to H is itself an abelian group: the sum h + k of two homomorphisms is defined by
- (h + k)(u) = h(u) + k(u) for all u in G.
The commutativity of H is needed to prove that h + k is again a group homomorphism.
The addition of homomorphisms is compatible with the composition of homomorphisms in the following sense: if f is in Hom(K, G), h, k are elements of Hom(G, H), and g is in Hom(H, L), then
- (h + k) ∘ f = (h ∘ f) + (k ∘ f) and g ∘ (h + k) = (g ∘ h) + (g ∘ k).
Since the composition is associative, this shows that the set End(G) of all endomorphisms of an abelian group forms a ring, the endomorphism ring of G. For example, the endomorphism ring of the abelian group consisting of the direct sum of m copies of Z/nZ is isomorphic to the ring of m-by-m matrices with entries in Z/nZ. The above compatibility also shows that the category of all abelian groups with group homomorphisms forms a preadditive category; the existence of direct sums and well-behaved kernels makes this category the prototypical example of an abelian category.
See also
References
- Dummit, D. S.; Foote, R. (2004). Abstract Algebra (3rd ed.). Wiley. pp. 71–72. ISBN 978-0-471-43334-7.
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556, Zbl 0984.00001
External links
- Rowland, Todd & Weisstein, Eric W. "Group Homomorphism". MathWorld.
 )
)


 be the identity element of the (H, ·) group and
be the identity element of the (H, ·) group and  , then
, then

 (or applying the cancellation rule) we obtain
(or applying the cancellation rule) we obtain


 .
.


 and show
and show  for arbitrary
for arbitrary  :
:





 , defined by
, defined by  is a homomorphism.
is a homomorphism. and
and  , represented respectively by
, represented respectively by  and
and  , where
, where  is the positive real numbers. Then, the function
is the positive real numbers. Then, the function  defined by the
defined by the