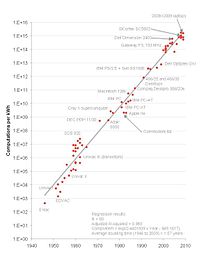
Koomey's law describes a trend in the history of computing hardware: for about a half-century, the number of computations per joule of energy dissipated doubled about every 1.57 years. Professor Jonathan Koomey described the trend in a 2010 paper in which he wrote that "at a fixed computing load, the amount of battery you need will fall by a factor of two every year and a half."
This trend had been remarkably stable since the 1950s (R of over 98%). But in 2011, Koomey re-examined this data and found that after 2000, the doubling slowed to about once every 2.6 years. This is related to the slowing of Moore's law, the ability to build smaller transistors; and the end around 2005 of Dennard scaling, the ability to build smaller transistors with constant power density.
"The difference between these two growth rates is substantial. A doubling every year and a half results in a 100-fold increase in efficiency every decade. A doubling every two and a half years yields just a 16-fold increase", Koomey wrote.
Implications
The implications of Koomey's law are that the amount of battery needed for a fixed computing load will fall by a factor of 100 every decade. As computing devices become smaller and more mobile, this trend may be even more important than improvements in raw processing power for many applications. Furthermore, energy costs are becoming an increasing factor in the economics of data centers, further increasing the importance of Koomey's law.
The slowing of Koomey's law has implications for energy use in information and communications technology. However, because computers do not run at peak output continuously, the effect of this slowing may not be seen for a decade or more. Koomey writes that "as with any exponential trend, this one will eventually end...in a decade or so, energy use will once again be dominated by the power consumed when a computer is active. And that active power will still be hostage to the physics behind the slowdown in Moore's Law."
History
Koomey was the lead author of the article in IEEE Annals of the History of Computing that first documented the trend. At about the same time, Koomey published a short piece about it in IEEE Spectrum.
It was further discussed in MIT Technology Review, and in a post by Erik Brynjolfsson on the "Economics of Information" blog, and at The Economist online.
The trend was previously known for digital signal processors, and it was then named "Gene's law". The name came from Gene Frantz, an electrical engineer at Texas Instruments. Frantz had documented that power dissipation in DSPs had been reduced by half every 18 months, over a 25-year period.
Slowing and end of Koomey's law
Latest studies indicate that Koomey's Law has slowed to doubling every 2.6 years. This rate is a statistical average over many technologies and many years, but there are exceptions. For example, in 2020 AMD reported that, since 2014, the company has managed to improve the efficiency of its mobile processors by a factor of 31.7, which is a doubling rate of 1.2 years. In June 2020, Koomey responded to the report, writing, "I have reviewed the data and can report that AMD exceeded the 25×20 goal it set in 2014 through improved design, superior optimization, and a laser-like focus on energy efficiency."
By the second law of thermodynamics and Landauer's principle, irreversible computing cannot continue to be made more energy efficient forever. Assuming that the energy efficiency of computing will continue to double every 2.6 years, and taking the most efficient super computer as of 2022, the Landauer bound will be reached around 2080. Thus, after this point, Koomey's law can no longer hold. Landauer's principle, however, does not constrain the efficiency of reversible computing. This, in conjunction with other Beyond CMOS computing technologies, could permit continued advances in efficiency.
See also
References
- ^ Koomey, Jonathan; Berard, Stephen; Sanchez, Marla; Wong, Henry (March 29, 2010), "Implications of Historical Trends in the Electrical Efficiency of Computing", IEEE Annals of the History of Computing, 33 (3): 46–54, doi:10.1109/MAHC.2010.28, ISSN 1058-6180, S2CID 8305701.
- ^ Koomey, Jonathan G. (November 29, 2016). "Our latest on energy efficiency of computing over time, now out in Electronic Design".
- Clark, Don (July 16, 2015). "Intel Rechisels the Tablet on Moore's Law". Wall Street Journal.
- Naffziger, Sam; Koomey, Jonathan (November 29, 2016). "Energy Efficiency of Computing: What's Next?". Electronic Design.
- ^ Brynjolfsson, Erik (September 12, 2011). "Is Koomey's Law eclipsing Moore's Law?". Economics of Information Blog. MIT.
- Koomey, Jonathan; Naffziger, Samuel (March 31, 2015). "Moore's Law Might Be Slowing Down, But Not Energy Efficiency". IEEE Spectrum.
- Koomey, J. G. (February 26, 2010), "Outperforming Moore's Law", IEEE Spectrum, 47 (3): 68, doi:10.1109/MSPEC.2010.5421913, S2CID 36759624.
- Greene, Kate (September 12, 2011). "A New and Improved Moore's Law". MIT Technology Review.
- "Computing power—A deeper law than Moore's?". The Economist online. October 10, 2011.
- Farncombe, Troy; Iniewski, Kris (2013), "§1.7.4 Power Dissipation", Medical Imaging: Technology and Applications, CRC Press, pp. 16–18, ISBN 978-1-4665-8263-7.
- Frantz, G. (2000), "Digital signal processor trends", IEEE Micro, 20 (6): 52–59, doi:10.1109/40.888703
- ^ Thurrott, Paul (June 25, 2020). "AMD Delivers a Major Mobile Efficiency Milestone".
- "Top 500 - Efficiency, Power, ..." Archived from the original on May 10, 2022. Retrieved May 26, 2022.
Further reading
- Koomey, J.; Naffziger, S. (March 31, 2015), "Moore's Law Might Be Slowing Down, But Not Energy Efficiency", IEEE Spectrum.
- Denning, Peter J.; Lewis, Ted G. (2017), "Exponential laws of computing growth", Communications of the ACM, 60: 54–65, doi:10.1145/2976758, hdl:10945/59477, S2CID 1359609.
| Computer laws | |
|---|---|
| Semantically, a computer law is not a hard and fast law, but a rule of thumb, or axiom (postulation) |