| Logical connectives | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||
| Related concepts | ||||||||||||||||||||||||||
| Applications | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set (usually {true, false}, {0,1} or {-1,1}). Alternative names are switching function, used especially in older computer science literature, and truth function (or logical function), used in logic. Boolean functions are the subject of Boolean algebra and switching theory.
A Boolean function takes the form , where is known as the Boolean domain and is a non-negative integer called the arity of the function. In the case where , the function is a constant element of . A Boolean function with multiple outputs, with is a vectorial or vector-valued Boolean function (an S-box in symmetric cryptography).
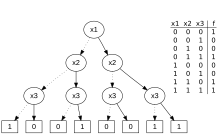
There are different Boolean functions with arguments; equal to the number of different truth tables with entries.
Every -ary Boolean function can be expressed as a propositional formula in variables , and two propositional formulas are logically equivalent if and only if they express the same Boolean function.
Examples
The rudimentary symmetric Boolean functions (logical connectives or logic gates) are:
- NOT, negation or complement - which receives one input and returns true when that input is false ("not")
- AND or conjunction - true when all inputs are true ("both")
- OR or disjunction - true when any input is true ("either")
- XOR or exclusive disjunction - true when one of its inputs is true and the other is false ("not equal")
- NAND or Sheffer stroke - true when it is not the case that all inputs are true ("not both")
- NOR or logical nor - true when none of the inputs are true ("neither")
- XNOR or logical equality - true when both inputs are the same ("equal")
An example of a more complicated function is the majority function (of an odd number of inputs).
Representation

A Boolean function may be specified in a variety of ways:
- Truth table: explicitly listing its value for all possible values of the arguments
- Marquand diagram: truth table values arranged in a two-dimensional grid (used in a Karnaugh map)
- Binary decision diagram, listing the truth table values at the bottom of a binary tree
- Venn diagram, depicting the truth table values as a colouring of regions of the plane
Algebraically, as a propositional formula using rudimentary Boolean functions:
- Negation normal form, an arbitrary mix of AND and ORs of the arguments and their complements
- Disjunctive normal form, as an OR of ANDs of the arguments and their complements
- Conjunctive normal form, as an AND of ORs of the arguments and their complements
- Canonical normal form, a standardized formula which uniquely identifies the function:
- Algebraic normal form or Zhegalkin polynomial, as a XOR of ANDs of the arguments (no complements allowed)
- Full (canonical) disjunctive normal form, an OR of ANDs each containing every argument or complement (minterms)
- Full (canonical) conjunctive normal form, an AND of ORs each containing every argument or complement (maxterms)
- Blake canonical form, the OR of all the prime implicants of the function
Boolean formulas can also be displayed as a graph:
- Propositional directed acyclic graph
- Digital circuit diagram of logic gates, a Boolean circuit
- And-inverter graph, using only AND and NOT
In order to optimize electronic circuits, Boolean formulas can be minimized using the Quine–McCluskey algorithm or Karnaugh map.
Analysis
See also: Analysis of Boolean functionsProperties
A Boolean function can have a variety of properties:
- Constant: Is always true or always false regardless of its arguments.
- Monotone: for every combination of argument values, changing an argument from false to true can only cause the output to switch from false to true and not from true to false. A function is said to be unate in a certain variable if it is monotone with respect to changes in that variable.
- Linear: for each variable, flipping the value of the variable either always makes a difference in the truth value or never makes a difference (a parity function).
- Symmetric: the value does not depend on the order of its arguments.
- Read-once: Can be expressed with conjunction, disjunction, and negation with a single instance of each variable.
- Balanced: if its truth table contains an equal number of zeros and ones. The Hamming weight of the function is the number of ones in the truth table.
- Bent: its derivatives are all balanced (the autocorrelation spectrum is zero)
- Correlation immune to mth order: if the output is uncorrelated with all (linear) combinations of at most m arguments
- Evasive: if evaluation of the function always requires the value of all arguments
- A Boolean function is a Sheffer function if it can be used to create (by composition) any arbitrary Boolean function (see functional completeness)
- The algebraic degree of a function is the order of the highest order monomial in its algebraic normal form
Circuit complexity attempts to classify Boolean functions with respect to the size or depth of circuits that can compute them.
Derived functions
A Boolean function may be decomposed using Boole's expansion theorem in positive and negative Shannon cofactors (Shannon expansion), which are the (k-1)-ary functions resulting from fixing one of the arguments (to zero or one). The general (k-ary) functions obtained by imposing a linear constraint on a set of inputs (a linear subspace) are known as subfunctions.
The Boolean derivative of the function to one of the arguments is a (k-1)-ary function that is true when the output of the function is sensitive to the chosen input variable; it is the XOR of the two corresponding cofactors. A derivative and a cofactor are used in a Reed–Muller expansion. The concept can be generalized as a k-ary derivative in the direction dx, obtained as the difference (XOR) of the function at x and x + dx.
The Möbius transform (or Boole-Möbius transform) of a Boolean function is the set of coefficients of its polynomial (algebraic normal form), as a function of the monomial exponent vectors. It is a self-inverse transform. It can be calculated efficiently using a butterfly algorithm ("Fast Möbius Transform"), analogous to the Fast Fourier Transform. Coincident Boolean functions are equal to their Möbius transform, i.e. their truth table (minterm) values equal their algebraic (monomial) coefficients. There are 2^2^(k−1) coincident functions of k arguments.
Cryptographic analysis
The Walsh transform of a Boolean function is a k-ary integer-valued function giving the coefficients of a decomposition into linear functions (Walsh functions), analogous to the decomposition of real-valued functions into harmonics by the Fourier transform. Its square is the power spectrum or Walsh spectrum. The Walsh coefficient of a single bit vector is a measure for the correlation of that bit with the output of the Boolean function. The maximum (in absolute value) Walsh coefficient is known as the linearity of the function. The highest number of bits (order) for which all Walsh coefficients are 0 (i.e. the subfunctions are balanced) is known as resiliency, and the function is said to be correlation immune to that order. The Walsh coefficients play a key role in linear cryptanalysis.
The autocorrelation of a Boolean function is a k-ary integer-valued function giving the correlation between a certain set of changes in the inputs and the function output. For a given bit vector it is related to the Hamming weight of the derivative in that direction. The maximal autocorrelation coefficient (in absolute value) is known as the absolute indicator. If all autocorrelation coefficients are 0 (i.e. the derivatives are balanced) for a certain number of bits then the function is said to satisfy the propagation criterion to that order; if they are all zero then the function is a bent function. The autocorrelation coefficients play a key role in differential cryptanalysis.
The Walsh coefficients of a Boolean function and its autocorrelation coefficients are related by the equivalent of the Wiener–Khinchin theorem, which states that the autocorrelation and the power spectrum are a Walsh transform pair.
Linear approximation table
These concepts can be extended naturally to vectorial Boolean functions by considering their output bits (coordinates) individually, or more thoroughly, by looking at the set of all linear functions of output bits, known as its components. The set of Walsh transforms of the components is known as a Linear Approximation Table (LAT) or correlation matrix; it describes the correlation between different linear combinations of input and output bits. The set of autocorrelation coefficients of the components is the autocorrelation table, related by a Walsh transform of the components to the more widely used Difference Distribution Table (DDT) which lists the correlations between differences in input and output bits (see also: S-box).
Real polynomial form
On the unit hypercube
Any Boolean function can be uniquely extended (interpolated) to the real domain by a multilinear polynomial in , constructed by summing the truth table values multiplied by indicator polynomials:For example, the extension of the binary XOR function iswhich equalsSome other examples are negation (), AND () and OR (). When all operands are independent (share no variables) a function's polynomial form can be found by repeatedly applying the polynomials of the operators in a Boolean formula. When the coefficients are calculated modulo 2 one obtains the algebraic normal form (Zhegalkin polynomial).
Direct expressions for the coefficients of the polynomial can be derived by taking an appropriate derivative:this generalizes as the Möbius inversion of the partially ordered set of bit vectors:where denotes the weight of the bit vector . Taken modulo 2, this is the Boolean Möbius transform, giving the algebraic normal form coefficients:In both cases, the sum is taken over all bit-vectors a covered by m, i.e. the "one" bits of a form a subset of the one bits of m.
When the domain is restricted to the n-dimensional hypercube , the polynomial gives the probability of a positive outcome when the Boolean function f is applied to n independent random (Bernoulli) variables, with individual probabilities x. A special case of this fact is the piling-up lemma for parity functions. The polynomial form of a Boolean function can also be used as its natural extension to fuzzy logic.
On the symmetric hypercube
Often, the Boolean domain is taken as , with false ("0") mapping to 1 and true ("1") to -1 (see Analysis of Boolean functions). The polynomial corresponding to is then given by:Using the symmetric Boolean domain simplifies certain aspects of the analysis, since negation corresponds to multiplying by -1 and linear functions are monomials (XOR is multiplication). This polynomial form thus corresponds to the Walsh transform (in this context also known as Fourier transform) of the function (see above). The polynomial also has the same statistical interpretation as the one in the standard Boolean domain, except that it now deals with the expected values (see piling-up lemma for an example).
Applications
Boolean functions play a basic role in questions of complexity theory as well as the design of processors for digital computers, where they are implemented in electronic circuits using logic gates.
The properties of Boolean functions are critical in cryptography, particularly in the design of symmetric key algorithms (see substitution box).
In cooperative game theory, monotone Boolean functions are called simple games (voting games); this notion is applied to solve problems in social choice theory.
See also
- Pseudo-Boolean function
- Boolean-valued function
- Boolean algebra topics
- Algebra of sets
- Decision tree model
- Indicator function
- Signed set
References
- "Boolean function - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-05-03.
- Weisstein, Eric W. "Boolean Function". mathworld.wolfram.com. Retrieved 2021-05-03.
- "switching function". TheFreeDictionary.com. Retrieved 2021-05-03.
- Davies, D. W. (December 1957). "Switching Functions of Three Variables". IRE Transactions on Electronic Computers. EC-6 (4): 265–275. doi:10.1109/TEC.1957.5222038. ISSN 0367-9950.
- McCluskey, Edward J. (2003-01-01), "Switching theory", Encyclopedia of Computer Science, GBR: John Wiley and Sons Ltd., pp. 1727–1731, ISBN 978-0-470-86412-8, retrieved 2021-05-03
- ^ Carlet, Claude. "Vectorial Boolean Functions for Cryptography" (PDF). University of Paris. Archived (PDF) from the original on 2016-01-17.
- ^ "Boolean functions — Sage 9.2 Reference Manual: Cryptography". doc.sagemath.org. Retrieved 2021-05-01.
- ^ Tarannikov, Yuriy; Korolev, Peter; Botev, Anton (2001). "Autocorrelation Coefficients and Correlation Immunity of Boolean Functions". In Boyd, Colin (ed.). Advances in Cryptology — ASIACRYPT 2001. Lecture Notes in Computer Science. Vol. 2248. Berlin, Heidelberg: Springer. pp. 460–479. doi:10.1007/3-540-45682-1_27. ISBN 978-3-540-45682-7.
- Carlet, Claude (2010), "Boolean Functions for Cryptography and Error-Correcting Codes" (PDF), Boolean Models and Methods in Mathematics, Computer Science, and Engineering, Encyclopedia of Mathematics and its Applications, Cambridge: Cambridge University Press, pp. 257–397, ISBN 978-0-521-84752-0, retrieved 2021-05-17
- Pieprzyk, Josef; Wang, Huaxiong; Zhang, Xian-Mo (2011-05-01). "Mobius transforms, coincident Boolean functions and non-coincidence property of Boolean functions". International Journal of Computer Mathematics. 88 (7): 1398–1416. doi:10.1080/00207160.2010.509428. ISSN 0020-7160. S2CID 9580510.
- Nitaj, Abderrahmane; Susilo, Willy; Tonien, Joseph (2017-10-01). "Dirichlet product for boolean functions". Journal of Applied Mathematics and Computing. 55 (1): 293–312. doi:10.1007/s12190-016-1037-4. ISSN 1865-2085. S2CID 16760125.
- Canteaut, Anne; Carlet, Claude; Charpin, Pascale; Fontaine, Caroline (2000-05-14). "Propagation characteristics and correlation-immunity of highly nonlinear boolean functions". Proceedings of the 19th International Conference on Theory and Application of Cryptographic Techniques. EUROCRYPT'00. Bruges, Belgium: Springer-Verlag: 507–522. ISBN 978-3-540-67517-4.
- ^ Heys, Howard M. "A Tutorial on Linear and Differential Cryptanalysis" (PDF). Archived (PDF) from the original on 2017-05-17.
- ^ "S-Boxes and Their Algebraic Representations — Sage 9.2 Reference Manual: Cryptography". doc.sagemath.org. Retrieved 2021-05-04.
- Daemen, Joan; Govaerts, René; Vandewalle, Joos (1994). "Correlation matrices". In Preneel, Bart (ed.). Fast Software Encryption: Second International Workshop. Leuven, Belgium, 14-16 December 1994, Proceedings. Lecture Notes in Computer Science. Vol. 1008. Springer. pp. 275–285. doi:10.1007/3-540-60590-8_21.
- Daemen, Joan (10 June 1998). "Chapter 5: Propagation and Correlation - Annex to AES Proposal Rijndael" (PDF). NIST. Archived (PDF) from the original on 2018-07-23.
- Nyberg, Kaisa (December 1, 2019). "The Extended Autocorrelation and Boomerang Tables and Links Between Nonlinearity Properties of Vectorial Boolean Functions" (PDF). Archived (PDF) from the original on 2020-11-02.
Further reading
- Crama, Yves; Hammer, Peter L. (2011), Boolean Functions: Theory, Algorithms, and Applications, Cambridge University Press, doi:10.1017/CBO9780511852008, ISBN 9780511852008
- "Boolean function", Encyclopedia of Mathematics, EMS Press, 2001
- Janković, Dragan; Stanković, Radomir S.; Moraga, Claudio (November 2003). "Arithmetic expressions optimisation using dual polarity property". Serbian Journal of Electrical Engineering. 1 (71–80, number 1): 71–80. doi:10.2298/SJEE0301071J.
- Arnold, Bradford Henry (1 January 2011). Logic and Boolean Algebra. Courier Corporation. ISBN 978-0-486-48385-6.
- Mano, M. M.; Ciletti, M. D. (2013), Digital Design, Pearson
| Mathematical logic | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||
| Theorems (list) and paradoxes | |||||||||
| Logics |
| ||||||||
| Set theory |
| ||||||||
| Formal systems (list), language and syntax |
| ||||||||
| Proof theory | |||||||||
| Model theory | |||||||||
| Computability theory | |||||||||
| Related | |||||||||
| Function | |
|---|---|
| Types by domain and codomain | |
| Classes/properties | |
| Constructions | |
| Generalizations | |













 , where
, where  is known as the
is known as the  is a non-negative integer called the
is a non-negative integer called the  , the function is a constant element of
, the function is a constant element of  with
with  is a vectorial or vector-valued Boolean function (an
is a vectorial or vector-valued Boolean function (an  different Boolean functions with
different Boolean functions with  entries.
entries.
 , and two propositional formulas are
, and two propositional formulas are  can be uniquely extended (interpolated) to the
can be uniquely extended (interpolated) to the  , constructed by summing the truth table values multiplied by
, constructed by summing the truth table values multiplied by  For example, the extension of the binary XOR function
For example, the extension of the binary XOR function  is
is which equals
which equals Some other examples are negation (
Some other examples are negation ( ), AND (
), AND ( ) and OR (
) and OR ( ). When all operands are independent (share no variables) a function's polynomial form can be found by repeatedly applying the polynomials of the operators in a Boolean formula. When the coefficients are calculated
). When all operands are independent (share no variables) a function's polynomial form can be found by repeatedly applying the polynomials of the operators in a Boolean formula. When the coefficients are calculated  this generalizes as the
this generalizes as the  where
where  denotes the weight of the bit vector
denotes the weight of the bit vector  . Taken modulo 2, this is the
. Taken modulo 2, this is the  In both cases, the sum is taken over all bit-vectors a covered by m, i.e. the "one" bits of a form a subset of the one bits of m.
In both cases, the sum is taken over all bit-vectors a covered by m, i.e. the "one" bits of a form a subset of the one bits of m.
 , the polynomial
, the polynomial  gives the probability of a positive outcome when the Boolean function f is applied to n independent random (
gives the probability of a positive outcome when the Boolean function f is applied to n independent random ( , with false ("0") mapping to 1 and true ("1") to -1 (see
, with false ("0") mapping to 1 and true ("1") to -1 (see  is then given by:
is then given by: Using the symmetric Boolean domain simplifies certain aspects of the
Using the symmetric Boolean domain simplifies certain aspects of the  (see
(see