
A lumped parameter cardiovascular model is a zero-dimensional mathematical model used to describe the hemodynamics of the cardiovascular system. Given a set of parameters that have a physical meaning (e.g. resistances to blood flow), it allows to study the changes in blood pressures or flow rates throughout the cardiovascular system. Modifying the parameters, it is possible to study the effects of a specific disease. For example, arterial hypertension is modeled increasing the arterial resistances of the model.
The lumped parameter model is used to study the hemodynamics of a three-dimensional space (the cardiovascular system) by means of a zero-dimensional space that exploits the analogy between pipes and electrical circuits. The reduction from three to zero dimensions is performed by splitting the cardiovascular system into different compartments, each of them representing a specific component of the system, e.g. right atrium or systemic arteries. Each compartment is made up of simple circuital components, like resistances or capacitors, while the blood flux behaves like the current flowing through the circuit according to Kirchoff's laws, under the action of the blood pressure (voltage drop).
The lumped parameter model consists in a system of ordinary differential equations that describes the evolution in time of the volumes of the heart chambers, and the blood pressures and fluxes through the blood vessels.
Model description
The lumped parameter model consists in a system of ordinary differential equations that adhere to the principles of conservation of mass and momentum balance. The model is obtained exploiting the electrical analogy where the current represents the blood flow, the voltage represents the pressure difference, the electric resistance plays the role of the vascular resistance (determined by the section and the length of the blood vessel), the capacitance plays the role of the vascular compliance (the ability of the vessel to distend and increase volume with increasing transmural pressure, that is the difference in pressure between two sides of a vessel wall) and the inductance represents the blood inertia. Each heart chamber is modeled by means of the elastances that describe the contractility of the cardiac muscle and the unloaded volume, that is the blood volume contained in the chamber at zero-pressure. The valves are modeled as diodes. The parameter of the model are the resistances, the capacitances, the inductances and the elastances. The unknowns of the system are the blood volumes inside each heart chamber, the blood pressures and fluxes inside each compartment of the circulation. The system of ordinary differential equations is solved by means of a numerical method for temporal discretization, e.g., a Runge-Kutta method.
The cardiovascular system is split into different compartments:
- the four heart chambers: left and right atrium and left and right ventricles;
- the systemic circulation that can be split into arteries, veins and, if needed, in other compartments accounting for different blood vessels;
- the pulmonary circulation that can be split into arteries, veins and, if needed, in other compartments accounting for different blood vessels.
Downstream of the left atrium and ventricle and right atrium and ventricle there are the four cardiac valves: mitral, aortic, tricuspid and pulmonary valves, respectively.
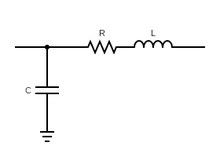
The splitting of the pulmonary and systemic circulation is not fixed, for example, if the interest of the study is in systemic capillaries, the compartment accounting for the systemic capillaries can be added to the lumped parameter model. Each compartment is described by a Windkessel circuit with the number of elements depending on the specific compartment. The ordinary differential equations of the model are derived from the Windkessel circuits and the Kirchoff's laws.
In what follows the focus will be on a specific lumped parameter model. The compartments considered are the four heart chambers, the systemic and pulmonary arteries and veins.
Heart chambers equations
The parameters related to the four heart chambers are the passive and active elastances and (where the subscript varies among and if the elastances refer to the right atrium or ventricle or the left atrium or ventricle, respectively) and the unloaded volumes . The dynamics of the heart chambers are described by the time-dependent elastance:
where is a periodic (with period of an heartbeat) time dependent function ranging from to that accounts for the activation phases of the heart during a heartbeat. From the above equation, the passive elastance represents the minimum elastance of the heart chamber, whereas the sum of and the maximum elastance of it. The time-dependent elastance allows the computation of the pressure inside a specific heart chamber as follows:
where is the volume of blood contained in the heart chamber and the volumes for each chamber are the solutions to the following ordinary differential equations that account for inward and outward blood fluxes associated with the heart chamber:
where and are the fluxes through the mitral, aortic, tricuspid and pulmonary valves respectively and and are the fluxes through the pulmonary and systemic veins, respectively.
Valves equations
The valves are modeled as diodes and the blood fluxes across the valves depend on the pressure jumps between the upstream and downstream compartment:
where the pressure inside each heart chamber is defined in the previous section, and are the time-dependent pressures inside the systemic and pulmonary artery compartment and is the flux across the valve depending on the pressure jump:
where and are the resistances of the valves when they are open and closed respectively.
Circulation compartments equations
Each compartment of the blood vessels is characterized by a combination of resistances, capacitances and inductances. For example, the arterial systemic circulation can be described by three parameters and that represent the arterial systemic resistance, capacitance and inductance. The ordinary differential equations that describes the systemic arterial circulation are:
where is the blood flux across the systemic arterial compartment and is the pressure inside the veins compartment.
Analogous equations with similar notation hold for the other compartments describing the blood circulation.
Ordinary differential equation system
Assembling the equations described above the following system is obtained: it holds
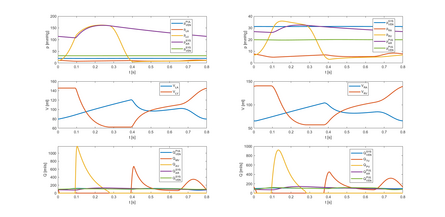
with the final time. The first two equations are related to the volumes in the left atrium and ventricles respectively. The equations from the third to the sixth are related to the pressures, and fluxes of the systemic arterial and venous systems. The last equations are related to the right heart and the pulmonary circulation in an analogous way. The system is completed with initial conditions for each of the unknowns.
From a mathematical point of view, the well-posedness of the problem is a consequence of the Cauchy–Lipschitz theorem, so its solution exists and it is unique. The solution of the system is approximated by means of a numerical method. The numerical simulation has to be computed for more than heartbeats (the final time depends on the number of heartbeats and the heart rate) to approach the limit cycle of the dynamical system, so that the solution behaves in a similar way to a periodic function emulating the periodicity of the cardiac cycle.
Further developments
The model described above is a specific lumped parameter model. It can be easily modified adding or removing compartments or circuit components inside any compartment as needed. The equations that govern the new or the modified compartments are the Kirchoff's laws as before.
The cardiovascular lumped parameter models can be enhanced adding a lumped parameter model for the respiratory system. As for the cardiovascular system, the respiratory system is split into different compartments modeling, for example, the larynx, the pharinx or the trachea. Moreover, the cardiopulmonary model can be combined with a model for blood oxygenation to study, for example, the levels of blood saturation.
There are several lumped parameter models and the choice of the model depends on the purpose of the work or the research. Complex models can describe different dynamics, but the increase in complexity entails a larger computational cost to solve the system of differential equations.
Some of the 0-D compartments of the lumped parameter model could be substituted by -dimensional components () to describe geometrically a specific component of the cardiovascular system (e.g., the 0-D compartment of the left ventricle can be substituted by a 3-D representation of it). As a consequence, the system of equations will include also partial differential equations to describe the dimensional components and it will entail a larger computational cost to be numerically solved.
See also
References
- ^ Shim, Eun Bo; Sah, Jong Youb; Youn, Chan Hyun (2004). "Mathematical Modeling of Cardiovascular System Dynamics Using a Lumped Parameter Method". The Japanese Journal of Physiology. 54 (6): 545–553. doi:10.2170/jjphysiol.54.545. ISSN 0021-521X. PMID 15760487.
- ^ Shi, Yubing; Lawford, Patricia; Hose, Rodney (2011). "Review of Zero-D and 1-D Models of Blood Flow in the Cardiovascular System". BioMedical Engineering OnLine. 10 (1): 33. doi:10.1186/1475-925X-10-33. ISSN 1475-925X. PMC 3103466. PMID 21521508.
- ^ Shim, Eun Bo; Sah, Jong Youb; Youn, Chan Hyun (2004). "Mathematical Modeling of Cardiovascular System Dynamics Using a Lumped Parameter Method". The Japanese Journal of Physiology. 54 (6): 545–553. doi:10.2170/jjphysiol.54.545. ISSN 0021-521X. PMID 15760487.
- ^ Shi, Yubing; Lawford, Patricia; Hose, Rodney (2011). "Review of Zero-D and 1-D Models of Blood Flow in the Cardiovascular System". BioMedical Engineering OnLine. 10 (1): 33. doi:10.1186/1475-925X-10-33. ISSN 1475-925X. PMC 3103466. PMID 21521508.
- ^ Dedè, Luca; Regazzoni, Francesco; Vergara, Christian; Zunino, Paolo; Guglielmo, Marco; Scrofani, Roberto; Fusini, Laura; Cogliati, Chiara; Pontone, Gianluca; Quarteroni, Alfio (2021). "Modeling the cardiac response to hemodynamic changes associated with COVID-19: a computational study". Mathematical Biosciences and Engineering. 18 (4): 3364–3383. doi:10.3934/mbe.2021168. hdl:2434/843779. ISSN 1551-0018. PMID 34198390. S2CID 234973850.
- Ngo, Chuong; Dahlmanns, Stephan; Vollmer, Thomas; Misgeld, Berno; Leonhardt, Steffen (2018-06-01). "An object-oriented computational model to study cardiopulmonary hemodynamic interactions in humans". Computer Methods and Programs in Biomedicine. 159: 167–183. doi:10.1016/j.cmpb.2018.03.008. ISSN 0169-2607. PMID 29650311. S2CID 4802953.
- Albanese, Antonio; Cheng, Limei; Ursino, Mauro; Chbat, Nicolas W. (2016-04-01). "An integrated mathematical model of the human cardiopulmonary system: model development". American Journal of Physiology. Heart and Circulatory Physiology. 310 (7): H899 – H921. doi:10.1152/ajpheart.00230.2014. ISSN 0363-6135. PMID 26683899.
- Lu, K.; Clark, J. W.; Ghorbel, F. H.; Ware, D. L.; Bidani, A. (2001-12-01). "A human cardiopulmonary system model applied to the analysis of the Valsalva maneuver". American Journal of Physiology. Heart and Circulatory Physiology. 281 (6): H2661 – H2679. doi:10.1152/ajpheart.2001.281.6.H2661. ISSN 0363-6135. PMID 11709436. S2CID 8246967.
- De Lazzari, C.; Darowski, M.; Ferrari, G.; Pisanelli, D.M.; Tosti, G. (2006). "Modelling in the study of interaction of Hemopump device and artificial ventilation". Computers in Biology and Medicine. 36 (11): 1235–1251. doi:10.1016/j.compbiomed.2005.08.001. PMID 16202402.
- Shi, Yubing; Korakianitis, Theodosios (2006). "Numerical Simulation of Cardiovascular Dynamics With Left Heart Failure and In-series Pulsatile Ventricular Assist Device". Artificial Organs. 30 (12): 929–948. doi:10.1111/j.1525-1594.2006.00326.x. ISSN 0160-564X. PMID 17181834.
- Heldt, Thomas; Shim, Eun B.; Kamm, Roger D.; Mark, Roger G. (2002-03-01). "Computational modeling of cardiovascular response to orthostatic stress". Journal of Applied Physiology. 92 (3): 1239–1254. doi:10.1152/japplphysiol.00241.2001. ISSN 8750-7587. PMID 11842064.
- Blanco, Pablo J.; Feijóo, Raúl A. (2010). "A 3D-1D-0D Computational Model for the Entire Cardiovascular System". Mecánica Computacional. 29 (59): 5887–5911.
- Baillargeon, Brian; Rebelo, Nuno; Fox, David D.; Taylor, Robert L.; Kuhl, Ellen (2014). "The Living Heart Project: A robust and integrative simulator for human heart function". European Journal of Mechanics - A/Solids. 48: 38–47. Bibcode:2014EuJMA..48...38B. doi:10.1016/j.euromechsol.2014.04.001. PMC 4175454. PMID 25267880.
Further reading
- Bazilevs, Yuri; Takizawa, Kenji; Tezduyar, Tayfun E. (2013). Computational fluid-structure interaction: methods and applications. Wiley series in computational mechanics. Chichester: Wiley. ISBN 978-0-470-97877-1.
- Quarteroni, Alfio; Dede', Luca; Manzoni, Andrea; Vergara, Christian (2019). Mathematical modelling of the human cardiovascular system: data, numerical approximation, clinical applications. Cambridge monographs on applied and computational mathematics. New York, NY: Cambridge University Press. ISBN 978-1-108-61609-6.
- Hirschvogel, Marc; Bassilious, Marina; Jagschies, Lasse; Wildhirt, Stephen M.; Gee, Michael W. (2017). "A monolithic 3D-0D coupled closed-loop model of the heart and the vascular system: Experiment-based parameter estimation for patient-specific cardiac mechanics: 3D-0D coupled closed-loop model of the heart". International Journal for Numerical Methods in Biomedical Engineering. 33 (8): e2842. doi:10.1002/cnm.2842. PMID 27743468. S2CID 36252500.
 and
and  (where the subscript
(where the subscript  varies among
varies among  and
and  if the elastances refer to the right atrium or ventricle or the left atrium or ventricle, respectively) and the unloaded volumes
if the elastances refer to the right atrium or ventricle or the left atrium or ventricle, respectively) and the unloaded volumes  . The dynamics of the heart chambers are described by the time-dependent elastance:
. The dynamics of the heart chambers are described by the time-dependent elastance:

 is a
is a  to
to  that accounts for the
that accounts for the  and
and 
 is the volume of blood contained in the heart chamber and the volumes for each chamber are the solutions to the following ordinary differential equations that account for inward and outward blood fluxes associated with the heart chamber:
is the volume of blood contained in the heart chamber and the volumes for each chamber are the solutions to the following ordinary differential equations that account for inward and outward blood fluxes associated with the heart chamber:




 and
and  are the fluxes through the mitral, aortic, tricuspid and pulmonary valves respectively and
are the fluxes through the mitral, aortic, tricuspid and pulmonary valves respectively and  and
and  are the fluxes through the pulmonary and systemic veins, respectively.
are the fluxes through the pulmonary and systemic veins, respectively.


 and
and  are the time-dependent pressures inside the systemic and pulmonary artery compartment and
are the time-dependent pressures inside the systemic and pulmonary artery compartment and  is the flux across the valve depending on the pressure jump:
is the flux across the valve depending on the pressure jump:

 and
and  are the resistances of the valves when they are open and closed respectively.
are the resistances of the valves when they are open and closed respectively.
 and
and  that represent the arterial systemic resistance, capacitance and inductance. The ordinary differential equations that describes the systemic arterial circulation are:
that represent the arterial systemic resistance, capacitance and inductance. The ordinary differential equations that describes the systemic arterial circulation are:


 is the blood flux across the systemic arterial compartment and
is the blood flux across the systemic arterial compartment and  is the pressure inside the veins compartment.
is the pressure inside the veins compartment.
 it holds
it holds

 the final time. The first two equations are related to the volumes in the left atrium and ventricles respectively. The equations from the third to the sixth are related to the pressures, and fluxes of the systemic arterial and venous systems. The last equations are related to the right heart and the pulmonary circulation in an analogous way. The system is completed with
the final time. The first two equations are related to the volumes in the left atrium and ventricles respectively. The equations from the third to the sixth are related to the pressures, and fluxes of the systemic arterial and venous systems. The last equations are related to the right heart and the pulmonary circulation in an analogous way. The system is completed with  heartbeats (the final time
heartbeats (the final time  -dimensional components (
-dimensional components ( ) to describe geometrically a specific component of the cardiovascular system (e.g., the 0-D compartment of the left ventricle can be substituted by a 3-D representation of it). As a consequence, the system of equations will include also
) to describe geometrically a specific component of the cardiovascular system (e.g., the 0-D compartment of the left ventricle can be substituted by a 3-D representation of it). As a consequence, the system of equations will include also