| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Carry-lookahead adder" – news · newspapers · books · scholar · JSTOR (August 2020) (Learn how and when to remove this message) |
| Part of a series on | |||||||
| Arithmetic logic circuits | |||||||
|---|---|---|---|---|---|---|---|
| Quick navigation | |||||||
| Theory | |||||||
Components
|
|||||||
| Categories | |||||||
| See also | |||||||
A carry-lookahead adder (CLA) or fast adder is a type of electronics adder used in digital logic. A carry-lookahead adder improves speed by reducing the amount of time required to determine carry bits. It can be contrasted with the simpler, but usually slower, ripple-carry adder (RCA), for which the carry bit is calculated alongside the sum bit, and each stage must wait until the previous carry bit has been calculated to begin calculating its own sum bit and carry bit. The carry-lookahead adder calculates one or more carry bits before the sum, which reduces the wait time to calculate the result of the larger-value bits of the adder.
Already in the mid-1800s, Charles Babbage recognized the performance penalty imposed by the ripple-carry used in his Difference Engine, and subsequently designed mechanisms for anticipating carriage for his never-built Analytical Engine. Konrad Zuse is thought to have implemented the first carry-lookahead adder in his 1930s binary mechanical computer, the Zuse Z1. Gerald B. Rosenberger of IBM filed for a patent on a modern binary carry-lookahead adder in 1957.
Two widely used implementations of the concept are the Kogge–Stone adder (KSA) and Brent–Kung adder (BKA).
Theory of operation
Ripple addition
A binary ripple-carry adder works in the same way as most pencil-and-paper methods of addition. Starting at the least significant digit position, the two corresponding digits are added and a result is obtained. A 'carry out' may occur if the result requires a higher digit; for example, "9 + 5 = 4, carry 1". Binary arithmetic works in the same fashion, with fewer digits. In this case, there are only four possible operations, 0+0, 0+1, 1+0 and 1+1; the 1+1 case generates a carry. Accordingly, all digit positions other than the rightmost one need to wait on the possibility of having to add an extra 1 from a carry on the digits one position to the right.
This means that no digit position can have an absolutely final value until it has been established whether or not a carry is coming in from the right. Moreover, if the sum without a carry is the highest value in the base (9 in base-10 pencil-and-paper methods or 1 in binary arithmetic), it is not possible to tell whether or not a given digit position is going to pass on a carry to the position on its left. At worst, when a whole sequence of sums comes to …99999999… (in decimal) or …11111111… (in binary), nothing can be deduced at all until the value of the carry coming in from the right is known; that carry must be propagated to the left, one step at a time, as each digit position evaluates "9 + 1 = 0, carry 1" or "1 + 1 = 0, carry 1". It is the "rippling" of the carry from right to left that gives the ripple-carry adder its name and slowness. When adding 32-bit integers, for instance, allowance has to be made for the possibility that a carry could have to ripple through every one of the 32 one-bit adders.
Lookahead
Carry-lookahead depends on two things:
- Calculating for each digit position whether that position is going to propagate a carry if one comes in from the right.
- Combining these calculated values to be able to deduce quickly whether, for each group of digits, that group is going to propagate a carry that comes in from the right.
Supposing that groups of four digits are chosen. The sequence of events would go like this:
- All 1-bit adders calculate their results. Simultaneously, the lookahead units perform their calculations.
- Assuming that a carry arises in a particular group, that carry will emerge at the left-hand end of the group within at most five gate delays and start propagating through the group to its left.
- If that carry is going to propagate all the way through the next group, the lookahead unit will already have deduced this. Accordingly, before the carry emerges from the next group, the lookahead unit is immediately (within one gate delay) able to tell the next group to the left that it is going to receive a carry – and, at the same time, to tell the next lookahead unit to the left that a carry is on its way.
The net effect is that the carries start by propagating slowly through each 4-bit group, just as in a ripple-carry system, but then move four times as fast, leaping from one lookahead-carry unit to the next. Finally, within each group that receives a carry, the carry propagates slowly within the digits in that group.
The more bits in a group, the more complex the lookahead carry logic becomes, and the more time is spent on the "slow roads" in each group rather than on the "fast road" between the groups (provided by the lookahead carry logic). On the other hand, the fewer bits there are in a group, the more groups have to be traversed to get from one end of a number to the other, and the less acceleration is obtained as a result.
Deciding the group size to be governed by lookahead carry logic requires a detailed analysis of gate and propagation delays for the particular technology being used.
It is possible to have more than one level of lookahead-carry logic, and this is in fact usually done. Each lookahead-carry unit already produces a signal saying "if a carry comes in from the right, I will propagate it to the left", and those signals can be combined so that each group of, say, four lookahead-carry units becomes part of a "supergroup" governing a total of 16 bits of the numbers being added. The "supergroup" lookahead-carry logic will be able to say whether a carry entering the supergroup will be propagated all the way through it, and using this information, it is able to propagate carries from right to left 16 times as fast as a naive ripple carry. With this kind of two-level implementation, a carry may first propagate through the "slow road" of individual adders, then, on reaching the left-hand end of its group, propagate through the "fast road" of 4-bit lookahead-carry logic, then, on reaching the left-hand end of its supergroup, propagate through the "superfast road" of 16-bit lookahead-carry logic.
Again, the group sizes to be chosen depend on the exact details of how fast signals propagate within logic gates and from one logic gate to another.
For very large numbers (hundreds or even thousands of bits), lookahead-carry logic does not become any more complex, because more layers of supergroups and supersupergroups can be added as necessary. The increase in the number of gates is also moderate: if all the group sizes are four, one would end up with one third as many lookahead carry units as there are adders. However, the "slow roads" on the way to the faster levels begin to impose a drag on the whole system (for instance, a 256-bit adder could have up to 24 gate delays in its carry processing), and the mere physical transmission of signals from one end of a long number to the other begins to be a problem. At these sizes, carry-save adders are preferable, since they spend no time on carry propagation at all.
Carry lookahead method
Carry-lookahead logic uses the concepts of generating and propagating carries. Although in the context of a carry-lookahead adder, it is most natural to think of generating and propagating in the context of binary addition, the concepts can be used more generally than this. In the descriptions below, the word digit can be replaced by bit when referring to binary addition of 2.
The addition of two 1-digit inputs A and B is said to generate if the addition will always carry, regardless of whether there is an input-carry (equivalently, regardless of whether any less significant digits in the sum carry). For example, in the decimal addition 52 + 67, the addition of the tens digits 5 and 6 generates because the result carries to the hundreds digit regardless of whether the ones digit carries; in the example, the ones digit does not carry (2 + 7 = 9). Even if the numbers were, say, 54 and 69, the addition of the tens digits 5 and 6 would still generate because the result once again carries to the hundreds digit independently of 4 and 9 creating a carrying.
In the case of binary addition, generates if and only if both A and B are 1. If we write to represent the binary predicate that is true if and only if generates, we have
where is an and.
The addition of two 1-digit inputs A and B is said to propagate if the addition will carry whenever there is an input carry (equivalently, when the next less significant digit in the sum carries). For example, in the decimal addition 37 + 62, the addition of the tens digits 3 and 6 propagate because the result would carry to the hundreds digit if the ones were to carry (which in this example, it does not). Note that propagate and generate are defined with respect to a single digit of addition and do not depend on any other digits in the sum.
In the case of binary addition, propagates if and only if at least one of A or B is 1. If is written to represent the binary predicate that is true if and only if propagates, one has
where on the right-hand side of the equation is an or.
Sometimes a slightly different definition of propagate is used. By this definition A + B is said to propagate if the addition will carry whenever there is an input carry, but will not carry if there is no input carry. Due to the way generate and propagate bits are used by the carry-lookahead logic, it doesn't matter which definition is used. In the case of binary addition, this definition is expressed by
where is an xor.
Table showing when carries are propagated or generated.
| Type of Carry | ||||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | None |
| 0 | 0 | 1 | 0 | None |
| 0 | 1 | 0 | 0 | None |
| 0 | 1 | 1 | 1 | Propagate |
| 1 | 0 | 0 | 0 | None |
| 1 | 0 | 1 | 1 | Propagate |
| 1 | 1 | 0 | 1 | Generate |
| 1 | 1 | 1 | 1 | Generate/Propagate |
For binary arithmetic, or is faster than xor and takes fewer transistors to implement. However, for a multiple-level carry-lookahead adder, it is simpler to use .
Given these concepts of generate and propagate, a digit of addition carries precisely when either the addition generates or the next less significant bit carries and the addition propagates. Written in Boolean algebra, with the carry bit of digit i, and and the propagate and generate bits of digit i respectively,
Implementation details


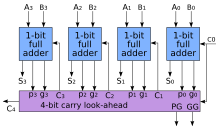
For each bit in a binary sequence to be added, the carry-lookahead logic will determine whether that bit pair will generate a carry or propagate a carry. This allows the circuit to "pre-process" the two numbers being added to determine the carry ahead of time. Then, when the actual addition is performed, there is no delay from waiting for the ripple-carry effect (or time it takes for the carry from the first full adder to be passed down to the last full adder).
To determine whether a bit pair will generate a carry, the following logic works:
To determine whether a bit pair will propagate a carry, either of the following logic statements work:
The reason why this works is based on evaluation of . The only difference in the truth tables between () and () is when both and are 1. However, if both and are 1, then the term is 1 (since its equation is ), and the term becomes irrelevant. The XOR is used normally within a basic full adder circuit; the OR is an alternative option (for a carry-lookahead only), which is far simpler in transistor-count terms.
For the example provided, the logic for the generate () and propagate () values are given below. The numeric value determines the signal from the circuit above, starting from 0 on the far right to 3 on the far left:
Substituting into , then into , then into yields the following expanded equations:
The carry-lookahead 4-bit adder can also be used in a higher-level circuit by having each CLA logic circuit produce a propagate and generate signal to a higher-level CLA logic circuit. The group propagate () and group generate () for a 4-bit CLA are:
They can then be used to create a carry-out for that particular 4-bit group:
It can be seen that this is equivalent to in previous equations.
Putting four 4-bit CLAs together yields four group propagates and four group generates. A lookahead-carry unit (LCU) takes these 8 values and uses identical logic to calculate in the CLAs. The LCU then generates the carry input for each of the 4 CLAs and a fifth equal to .
The calculation of the gate delay of a 16-bit adder (using 4 CLAs and 1 LCU) is not as straight forward as the ripple carry adder.
Starting at time of zero:
- calculation of and is done at time 1,
- calculation of the is done at time 2,
- calculation of the is done at time 3,
- calculation of the inputs for the CLAs from the LCU are done at:
- time 0 for the first CLA,
- time 5 for the second, third and fourth CLA,
- calculation of the are done at:
- time 4 for the first CLA,
- time 8 for the second, third & fourth CLA,
- calculation of the final carry bit () is done at time 5.
The maximal time is 8 gate delays (for ).
A standard 16-bit ripple-carry adder would take 16 × 2 − 1 = 31 gate delays.
Expansion
This example is a 4-bit carry look ahead adder, there are 5 outputs. Below is the expansion:
S0 = (A0 XOR B0) XOR Cin '2dt (dt - delay time)
S1 = (A1 XOR B1)
XOR ((A0 AND B0)
OR ((A0 XOR B0) AND Cin)) '4dt
S2 = (A2 XOR B2)
XOR ((A1 AND B1)
OR ((A1 XOR B1) AND (A0 AND B0))
OR ((A1 XOR B1) AND (A0 XOR B0) AND Cin)) '4dt
S3 = (A3 XOR B3)
XOR ((A2 AND B2)
OR ((A2 XOR B2) AND (A1 AND B1))
OR ((A2 XOR B2) AND (A1 XOR B1) AND (A0 AND B0))
OR ((A2 XOR B2) AND (A1 XOR B1) AND (A0 XOR B0) AND Cin)) '4dt
Cout = (A3 AND B3)
OR ((A3 XOR B3) AND (A2 AND B2))
OR ((A3 XOR B3) AND (A2 XOR B2) AND (A1 AND B1))
OR ((A3 XOR B3) AND (A2 XOR B2) AND (A1 XOR B1) AND (A0 AND B0))
OR ((A3 XOR B3) AND (A2 XOR B2) AND (A1 XOR B1) AND (A0 XOR B0) AND Cin) '3dt
More simple 4-bit carry-lookahead adder:
'Step 0
Gin = Cin '0dt
P00 = A0 XOR B0 '1dt
G00 = A0 AND B0 '1dt
P10 = A1 XOR B1 '1dt
G10 = A1 AND B1 '1dt
P20 = A2 XOR B2 '1dt
G20 = A2 AND B2 '1dt
P30 = A3 XOR B3 '1dt
G30 = A3 AND B3 '1dt
'Step 1
G01 = G00 OR_
P00 AND Gin '3dt, C0, valency-2
G11 = G10 OR_
P10 AND G00 OR_
P10 AND P00 AND Gin '3dt, C1, valency-3
G21 = G20 OR_
P20 AND G10 OR_
P20 AND P10 AND G00 OR_
P20 AND P10 AND P00 AND Gin '3dt, C2, valency-4
G31 = G30 OR_
P30 AND G20 OR_
P30 AND P20 AND G10 OR_
P30 AND P20 AND P10 AND G00 OR_
P30 AND P20 AND P10 AND P00 AND Gin '3dt, C3, valency-5
'Sum
S0 = P00 XOR Gin '2dt
S1 = P10 XOR G01 '4dt
S2 = P20 XOR G11 '4dt
S3 = P30 XOR G21 '4dt
S4 = G31 '3dt, Cout
Manchester carry chain
The Manchester carry chain is a variation of the carry-lookahead adder that uses shared logic to lower the transistor count. As can be seen above in the implementation section, the logic for generating each carry contains all of the logic used to generate the previous carries. A Manchester carry chain generates the intermediate carries by tapping off nodes in the gate that calculates the most significant carry value. However, not all logic families have these internal nodes, CMOS being a major example. Dynamic logic can support shared logic, as can transmission gate logic. One of the major downsides of the Manchester carry chain is that the capacitive load of all of these outputs, together with the resistance of the transistors causes the propagation delay to increase much more quickly than a regular carry lookahead. A Manchester-carry-chain section generally doesn't exceed 4 bits.
See also
References
- "Analytical Engine – History of Charles Babbage Analytical Engine". history-computer.com. 4 January 2021. Retrieved 2021-06-19.
- Babbage, Charles (1864). Passages from the Life of a Philosopher. London: Longman, Green, Longmand Roberts & Green. pp. 59–63, 114–116.
- Rojas, Raul (2014-06-07). "The Z1: Architecture and Algorithms of Konrad Zuse's First Computer". arXiv:1406.1886 .
- Rosenberger, Gerald B. (1960-12-27). "Simultaneous Carry Adder". U.S. Patent 2,966,305.
- "Manchester carry-chain adder - WikiChip". wikichip.org. Retrieved 2017-04-24.
Further reading
- Hardware algorithms for arithmetic modules, ARITH research group, Aoki lab., Tohoku University
- Katz, Randy (1994). "Contemporary Logic Design". Microelectronics Journal. 26 (5). The Benjamin/Cummings Publishing Company: 249–256. doi:10.1016/0026-2692(95)90052-7. ISBN 0-8053-2703-7.
- Savard, John J. G. (2018) . "Advanced Arithmetic Techniques". quadibloc. Archived from the original on 2018-07-03. Retrieved 2018-07-16.
 generates if and only if both A and B are 1. If we write
generates if and only if both A and B are 1. If we write  to represent the binary predicate that is true if and only if
to represent the binary predicate that is true if and only if 
 is an and.
is an and.
 is written to represent the binary predicate that is true if and only if
is written to represent the binary predicate that is true if and only if 

 is an xor.
is an xor.




 .
.
 and
and  the propagate and generate bits of digit i respectively,
the propagate and generate bits of digit i respectively,




 . The only difference in the truth tables between (
. The only difference in the truth tables between ( term is 1 (since its equation is
term is 1 (since its equation is  term becomes irrelevant. The XOR is used normally within a basic full adder circuit; the OR is an alternative option (for a carry-lookahead only), which is far simpler in transistor-count terms.
term becomes irrelevant. The XOR is used normally within a basic full adder circuit; the OR is an alternative option (for a carry-lookahead only), which is far simpler in transistor-count terms.
 ) and propagate (
) and propagate ( ) values are given below. The numeric value determines the signal from the circuit above, starting from 0 on the far right to 3 on the far left:
) values are given below. The numeric value determines the signal from the circuit above, starting from 0 on the far right to 3 on the far left:



 into
into  , then
, then  , then
, then  yields the following expanded equations:
yields the following expanded equations:



 ) and group generate (
) and group generate ( ) for a 4-bit CLA are:
) for a 4-bit CLA are:



 .
.
 are done at:
are done at:
 ).
).