| A joint Politics and Economics series |
| Social choice and electoral systems |
|---|
 |
|
Single-winner methodsSingle vote - plurality methods
|
|
Proportional representationParty-list
|
|
Mixed systemsBy results of combination
By mechanism of combination By ballot type |
|
Paradoxes and pathologiesSpoiler effects
Pathological response Paradoxes of majority rule |
Social and collective choiceImpossibility theorems
Positive results |
|
|
The McKelvey–Schofield chaos theorem is a result in social choice theory. It states that if preferences are defined over a multidimensional policy space, then choosing policies using majority rule is unstable. There will in most cases be no Condorcet winner and any policy can be enacted through a sequence of votes, regardless of the original policy. This means that adding more policies and changing the order of votes ("agenda manipulation") can be used to arbitrarily pick the winner.
Versions of the theorem have been proved for different types of preferences, with different classes of exceptions. A version of the theorem was first proved by Richard McKelvey in 1976, for preferences based on Euclidean distances in . Another version of the theorem was proved by Norman Schofield in 1978, for differentiable preferences.
The theorem can be thought of as showing that Arrow's impossibility theorem holds when preferences are restricted to be concave in . The median voter theorem shows that when preferences are restricted to be single-peaked on the real line, Arrow's theorem does not hold, and the median voter's ideal point is a Condorcet winner. The chaos theorem shows that this good news does not continue in multiple dimensions.
Definitions
The theorem considers a finite number of voters, n, who vote for policies which are represented as points in Euclidean space of dimension m. Each vote is between two policies using majority rule. Each voter, i, has a utility function, Ui, which measures how much they value different policies.
Euclidean preferences
Richard McKelvey considered the case when preferences are "Euclidean metrics". That means every voter's utility function has the form for all policies x and some xi, where d is the Euclidean distance and is a monotone decreasing function.
Under these conditions, there could be a collection of policies which don't have a Condorcet winner using majority rule. This means that, given a number of policies Xa, Xb, Xc, there could be a series of pairwise elections where:
- Xa wins over Xb
- Xb wins over Xc
- Xc wins over Xa
McKelvey proved that elections can be even more "chaotic" than that: If there is no equilibrium outcome then any two policies, e.g. A and B, have a sequence of policies, , where each one pairwise wins over the other in a series of elections, meaning:
- A wins over X1
- X1 wins over X2
- ...
- Xs wins over B
This is true regardless of whether A would beat B or vice versa.
Example
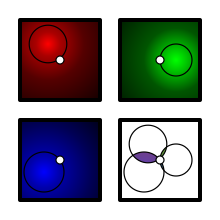
The simplest illustrating example is in two dimensions, with three voters. Each voter will then have a maximum preferred policy, and any other policy will have a corresponding circular indifference curve centered at the preferred policy. If a policy was proposed, then any policy in the intersection of two voters indifference curves would beat it. Any point in the plane will almost always have a set of points that are preferred by 2 out of 3 voters.
Generalisations
Norman Schofield extended the theorem to more general classes of utility functions, requiring only that they are differentiable. He also established conditions for the existence of a directed continuous path of policies, where each policy further along the path would win against one earlier. Some of Schofield's proofs were later found to be incorrect by Jeffrey S. Banks, who corrected his proofs.
References
- ^ Cox, Gary W.; Shepsle, Kenneth A. (2007). "Majority Cycling and Agenda Manipulation: Richard McKelvey's Contributions and Legacy". In Aldrich, John Herbert; Alt, James E.; Lupia, Arthur (eds.). Positive Changes in Political Science. Analytical perspectives on politics. Ann Arbor, Michigan: University of Michigan Press. pp. 20–23. ISBN 978-0-472-06986-6.
- McKelvey, Richard D. (June 1976). "Intransitivities in Multidimensional Voting Models and Some Implications for Agenda Control". Journal of Economic Theory. 12 (3): 472–482. doi:10.1016/0022-0531(76)90040-5.
- Schofield, N. (1 October 1978). "Instability of Simple Dynamic Games". The Review of Economic Studies. 45 (3): 575–594. doi:10.2307/2297259. JSTOR 2297259.
- Banks, Jeffrey S. (1995-01-01). "Singularity theory and core existence in the spatial model". Journal of Mathematical Economics. 24 (6): 523–536. doi:10.1016/0304-4068(94)00704-E. ISSN 0304-4068.
- Saari, Donald G. (2008). "Deliver Us from the Plurality Vote". Disposing dictators, demystifying voting paradoxes: social choice analysis. Cambridge, New York: Cambridge University Press. ISBN 978-0-521-51605-1. OCLC 227031682.
This economic theory related article is a stub. You can help Misplaced Pages by expanding it. |
 . Another version of the theorem was proved by
. Another version of the theorem was proved by  for all policies x and some xi, where d is the
for all policies x and some xi, where d is the  is a
is a  , where each one pairwise wins over the other in a series of elections, meaning:
, where each one pairwise wins over the other in a series of elections, meaning: