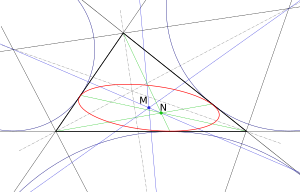
In geometry, the mittenpunkt (from German: middle point) of a triangle is a triangle center: a point defined from the triangle that is invariant under Euclidean transformations of the triangle. It was identified in 1836 by Christian Heinrich von Nagel as the symmedian point of the excentral triangle of the given triangle.
Coordinates
The mittenpunkt has trilinear coordinates
where a, b, and c are the side lengths of the given triangle. Expressed instead in terms of the angles A, B, and C, the trilinears are
The barycentric coordinates are
Collinearities
The mittenpunkt is at the intersection of the line connecting the centroid and the Gergonne point, the line connecting the incenter and the symmedian point and the line connecting the orthocenter with the Spieker center, thus establishing three collinearities involving the mittenpunkt.
Related figures
The three lines connecting the excenters of the given triangle to the corresponding edge midpoints all meet at the mittenpunkt; thus, it is the center of perspective of the excentral triangle and the median triangle, with the corresponding axis of perspective being the trilinear polar of the Gergonne point. The mittenpunkt is also the centroid of the Mandart inellipse of the given triangle, the ellipse tangent to the triangle at its extouch points.
Notes
The Mittenpunkt also serves as the Gergonne point of the Medial triangle.
References
- ^ Kimberling, Clark (1994), "Central Points and Central Lines in the Plane of a Triangle", Mathematics Magazine, 67 (3): 163–187, doi:10.2307/2690608, JSTOR 2690608, MR 1573021.
- v. Nagel, C. H. (1836), Untersuchungen über die wichtigsten zum Dreiecke gehörenden Kreise, Leipzig.
- ^ http://faculty.evansville.edu/ck6/encyclopedia/ETC.html Encyclopedia of Triangle Centers
- Paul Yiu, "The uses of homogeneous barycentric coordinates in plane euclidean geometry" http://lya.fciencias.unam.mx/gfgf/ga20071/data/material/barycentricpaper.pdf
- Eddy, Roland H. (1989), "A Desarguesian dual for Nagel's middlespoint", Elemente der Mathematik, 44 (3): 79–80, MR 0999636.
- Gibert, Bernard (2004), "Generalized Mandart conics" (PDF), Forum Geometricorum, 4: 177–198, MR 2130231, archived from the original (PDF) on 2016-03-03, retrieved 2012-09-02.


