
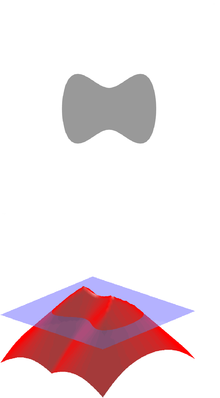
In mathematics and its applications, the signed distance function or signed distance field (SDF) is the orthogonal distance of a given point x to the boundary of a set Ω in a metric space (such as the surface of a geometric shape), with the sign determined by whether or not x is in the interior of Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω. However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside). The concept also sometimes goes by the name oriented distance function/field.
Definition
Let Ω be a subset of a metric space X with metric d, and be its boundary. The distance between a point x of X and the subset of X is defined as usual as
where denotes the infimum.
The signed distance function from a point x of X to is defined by
Properties in Euclidean space
If Ω is a subset of the Euclidean space R with piecewise smooth boundary, then the signed distance function is differentiable almost everywhere, and its gradient satisfies the eikonal equation
If the boundary of Ω is C for k ≥ 2 (see Differentiability classes) then d is C on points sufficiently close to the boundary of Ω. In particular, on the boundary f satisfies
where N is the inward normal vector field. The signed distance function is thus a differentiable extension of the normal vector field. In particular, the Hessian of the signed distance function on the boundary of Ω gives the Weingarten map.
If, further, Γ is a region sufficiently close to the boundary of Ω that f is twice continuously differentiable on it, then there is an explicit formula involving the Weingarten map Wx for the Jacobian of changing variables in terms of the signed distance function and nearest boundary point. Specifically, if T(∂Ω, μ) is the set of points within distance μ of the boundary of Ω (i.e. the tubular neighbourhood of radius μ), and g is an absolutely integrable function on Γ, then
where det denotes the determinant and dSu indicates that we are taking the surface integral.
Algorithms
Algorithms for calculating the signed distance function include the efficient fast marching method, fast sweeping method and the more general level-set method.
For voxel rendering, a fast algorithm for calculating the SDF in taxicab geometry uses summed-area tables.
Applications

Signed distance functions are applied, for example, in real-time rendering, for instance the method of SDF ray marching, and computer vision.
SDF has been used to describe object geometry in real-time rendering, usually in a raymarching context, starting in the mid 2000s. By 2007, Valve is using SDFs to render large pixel-size (or high DPI) smooth fonts with GPU acceleration in its games. Valve's method is not perfect as it runs in raster space in order to avoid the computational complexity of solving the problem in the (continuous) vector space. The rendered text often loses sharp corners. In 2014, an improved method was presented by Behdad Esfahbod. Behdad's GLyphy approximates the font's Bézier curves with arc splines, accelerated by grid-based discretization techniques (which culls too-far-away points) to run in real time.
A modified version of SDF was introduced as a loss function to minimise the error in interpenetration of pixels while rendering multiple objects. In particular, for any pixel that does not belong to an object, if it lies outside the object in rendition, no penalty is imposed; if it does, a positive value proportional to its distance inside the object is imposed.
In 2020, the FOSS game engine Godot 4.0 received SDF-based real-time global illumination (SDFGI), that became a compromise between more realistic voxel-based GI and baked GI. Its core advantage is that it can be applied to infinite space, which allows developers to use it for open-world games.
In 2023, the authors of the Zed text editor announced a GPUI framework that draws all UI elements using the GPU at 120 fps. The work makes use of Inigo Quilez's list of geometric primitives in SDF, Figma co-founder Evan Wallace's Gaussian blur in SDF, and a new rounded rectangle SDF.
See also
- Distance function
- Level-set method
- Eikonal equation
- Parallel curve (also known as offset curve)
- Signed arc length
- Signed area
- Signed measure
- Signed volume
Notes
- Chan, T.; Zhu, W. (2005). Level set based shape prior segmentation. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. doi:10.1109/CVPR.2005.212.
- Malladi, R.; Sethian, J.A.; Vemuri, B.C. (1995). "Shape modeling with front propagation: a level set approach". IEEE Transactions on Pattern Analysis and Machine Intelligence. 17 (2): 158–175. CiteSeerX 10.1.1.33.2443. doi:10.1109/34.368173. S2CID 9505101.
- Gilbarg & Trudinger 1983, Lemma 14.16.
- Gilbarg & Trudinger 1983, Equation (14.98).
- Zhao Hongkai. A fast sweeping method for eikonal equations. Mathematics of Computation, 2005, 74. Jg., Nr. 250, S. 603-627.
- Nilsson, Tobias (2019). "Optimization Methods for Direct Volume Rendering on the Client Side Web" (PDF). Digitala Vetenskapliga Arkivet. Retrieved 2022-07-08.
- Tomas Akenine-Möller; Eric Haines; Naty Hoffman (6 August 2018). Real-Time Rendering, Fourth Edition. CRC Press. ISBN 978-1-351-81615-1.
- Perera, S.; Barnes, N.; He, X.; Izadi, S.; Kohli, P.; Glocker, B. (January 2015). "Motion Segmentation of Truncated Signed Distance Function Based Volumetric Surfaces". 2015 IEEE Winter Conference on Applications of Computer Vision. pp. 1046–1053. doi:10.1109/WACV.2015.144. ISBN 978-1-4799-6683-7. S2CID 16811314.
- Izadi, Shahram; Kim, David; Hilliges, Otmar; Molyneaux, David; Newcombe, Richard; Kohli, Pushmeet; Shotton, Jamie; Hodges, Steve; Freeman, Dustin (2011). "KinectFusion". Proceedings of the 24th annual ACM symposium on User interface software and technology. UIST '11. New York, NY, USA: ACM. pp. 559–568. doi:10.1145/2047196.2047270. ISBN 9781450307161. S2CID 3345516.
- Green, Chris (2007). "Improved alpha-tested magnification for vector textures and special effects". ACM SIGGRAPH 2007 courses. pp. 9–18. CiteSeerX 10.1.1.170.9418. doi:10.1145/1281500.1281665. ISBN 9781450318235. S2CID 7479538.
- Behdad Esfahbod. GLyphy: high-quality glyph rendering using OpenGL ES2 shaders [linux.conf.au 2014]. YouTube. Archived from the original on 2021-12-11. Source Code
- Jiang, Wen; Kolotouros, Nikos; Pavlakos, Georgios; Zhou, Xiaowei; Daniilidis, Kostas (2020-06-15). "Coherent Reconstruction of Multiple Humans from a Single Image". arXiv:2006.08586 .
- Engine, Godot. "Godot 4.0 gets SDF based real-time global illumination". Godot Engine.
- Scandurra, Antonio (7 March 2023). "Leveraging Rust and the GPU to render user interfaces at 120 FPS - Zed Blog". Zed.
References
- Stanley J. Osher and Ronald P. Fedkiw (2003). Level Set Methods and Dynamic Implicit Surfaces. Springer. ISBN 9780387227467.
- Gilbarg, D.; Trudinger, N. S. (1983). Elliptic Partial Differential Equations of Second Order. Grundlehren der mathematischen Wissenschaften. Vol. 224 (2nd ed.). Springer-Verlag. (or the Appendix of the 1977 1st ed.)
 be its
be its 
 denotes the
denotes the  is defined by
is defined by




