
The Zeeman effect (/ˈzeɪmən/ ZAY-mən, Dutch: [ˈzeːmɑn]) is the splitting of a spectral line into several components in the presence of a static magnetic field. It is caused by interaction of the magnetic field with the magnetic moment of the atomic electron associated to its orbital motion and spin; this interaction shifts some orbital energies more than others, resulting in the split spectrum. The effect is named after the Dutch physicist Pieter Zeeman, who discovered it in 1896 and received a Nobel Prize in Physics for this discovery. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field. Also similar to the Stark effect, transitions between different components have, in general, different intensities, with some being entirely forbidden (in the dipole approximation), as governed by the selection rules.
Since the distance between the Zeeman sub-levels is a function of magnetic field strength, this effect can be used to measure magnetic field strength, e.g. that of the Sun and other stars or in laboratory plasmas.
Discovery
In 1896 Zeeman learned that his laboratory had one of Henry Augustus Rowland's highest resolving diffraction gratings. Zeeman had read James Clerk Maxwell's article in Encyclopædia Britannica describing Michael Faraday's failed attempts to influence light with magnetism. Zeeman wondered if the new spectrographic techniques could succeed where early efforts had not.
When illuminated by a slit shaped source, the grating produces a long array of slit images corresponding to different wavelengths. Zeeman placed a piece of asbestos soaked in salt water into a Bunsen burner flame at the source of the grating: he could easily see two lines for sodium light emission. Energizing a 10 kilogauss magnet around the flame he observed a slight broadening of the sodium images.
When Zeeman switched to cadmium as the source he observed the images split when the magnet was energized. These splittings could be analyzed with Hendrik Lorentz's then-new electron theory. In retrospect we now know that the magnetic effects on sodium require quantum mechanical treatment. Zeeman and Lorentz were awarded the 1902 Nobel prize; in his acceptance speech Zeeman explained his apparatus and showed slides of the spectrographic images.
Nomenclature
Historically, one distinguishes between the normal and an anomalous Zeeman effect (discovered by Thomas Preston in Dublin, Ireland). The anomalous effect appears on transitions where the net spin of the electrons is non-zero. It was called "anomalous" because the electron spin had not yet been discovered, and so there was no good explanation for it at the time that Zeeman observed the effect. Wolfgang Pauli recalled that when asked by a colleague as to why he looked unhappy, he replied, "How can one look happy when he is thinking about the anomalous Zeeman effect?"
At higher magnetic field strength the effect ceases to be linear. At even higher field strengths, comparable to the strength of the atom's internal field, the electron coupling is disturbed and the spectral lines rearrange. This is called the Paschen–Back effect.
In the modern scientific literature, these terms are rarely used, with a tendency to use just the "Zeeman effect". Another rarely used obscure term is inverse Zeeman effect, referring to the Zeeman effect in an absorption spectral line.
A similar effect, splitting of the nuclear energy levels in the presence of a magnetic field, is referred to as the nuclear Zeeman effect.
Theoretical presentation
The total Hamiltonian of an atom in a magnetic field is
where is the unperturbed Hamiltonian of the atom, and is the perturbation due to the magnetic field:
where is the magnetic moment of the atom. The magnetic moment consists of the electronic and nuclear parts; however, the latter is many orders of magnitude smaller and will be neglected here. Therefore,
where is the Bohr magneton, is the total electronic angular momentum, and is the Landé g-factor. A more accurate approach is to take into account that the operator of the magnetic moment of an electron is a sum of the contributions of the orbital angular momentum and the spin angular momentum , with each multiplied by the appropriate gyromagnetic ratio:
where and (the latter is called the anomalous gyromagnetic ratio; the deviation of the value from 2 is due to the effects of quantum electrodynamics). In the case of the LS coupling, one can sum over all electrons in the atom:
where and are the total spin momentum and spin of the atom, and averaging is done over a state with a given value of the total angular momentum.
If the interaction term is small (less than the fine structure), it can be treated as a perturbation; this is the Zeeman effect proper. In the Paschen–Back effect, described below, exceeds the LS coupling significantly (but is still small compared to ). In ultra-strong magnetic fields, the magnetic-field interaction may exceed , in which case the atom can no longer exist in its normal meaning, and one talks about Landau levels instead. There are intermediate cases which are more complex than these limit cases.
Weak field (Zeeman effect)
If the spin–orbit interaction dominates over the effect of the external magnetic field, and are not separately conserved, only the total angular momentum is. The spin and orbital angular momentum vectors can be thought of as precessing about the (fixed) total angular momentum vector . The (time-)"averaged" spin vector is then the projection of the spin onto the direction of :
and for the (time-)"averaged" orbital vector:
Thus,
Using and squaring both sides, we get
and: using and squaring both sides, we get
Combining everything and taking , we obtain the magnetic potential energy of the atom in the applied external magnetic field,
where the quantity in square brackets is the Landé g-factor gJ of the atom ( and ) and is the z-component of the total angular momentum. For a single electron above filled shells and , the Landé g-factor can be simplified into:
Taking to be the perturbation, the Zeeman correction to the energy is
Example: Lyman-alpha transition in hydrogen
The Lyman-alpha transition in hydrogen in the presence of the spin–orbit interaction involves the transitions
- and
In the presence of an external magnetic field, the weak-field Zeeman effect splits the 1S1/2 and 2P1/2 levels into 2 states each () and the 2P3/2 level into 4 states (). The Landé g-factors for the three levels are:
- for (j=1/2, l=0)
- for (j=1/2, l=1)
- for (j=3/2, l=1).
Note in particular that the size of the energy splitting is different for the different orbitals, because the gJ values are different. On the left, fine structure splitting is depicted. This splitting occurs even in the absence of a magnetic field, as it is due to spin–orbit coupling. Depicted on the right is the additional Zeeman splitting, which occurs in the presence of magnetic fields.
| Initial state
()
|
Final state
()
|
Energy perturbation |
|---|---|---|
Strong field (Paschen–Back effect)
The Paschen–Back effect is the splitting of atomic energy levels in the presence of a strong magnetic field. This occurs when an external magnetic field is sufficiently strong to disrupt the coupling between orbital () and spin () angular momenta. This effect is the strong-field limit of the Zeeman effect. When , the two effects are equivalent. The effect was named after the German physicists Friedrich Paschen and Ernst E. A. Back.
When the magnetic-field perturbation significantly exceeds the spin–orbit interaction, one can safely assume . This allows the expectation values of and to be easily evaluated for a state . The energies are simply
The above may be read as implying that the LS-coupling is completely broken by the external field. However and are still "good" quantum numbers. Together with the selection rules for an electric dipole transition, i.e., this allows to ignore the spin degree of freedom altogether. As a result, only three spectral lines will be visible, corresponding to the selection rule. The splitting is independent of the unperturbed energies and electronic configurations of the levels being considered.
More precisely, if , each of these three components is actually a group of several transitions due to the residual spin–orbit coupling and relativistic corrections (which are of the same order, known as 'fine structure'). The first-order perturbation theory with these corrections yields the following formula for the hydrogen atom in the Paschen–Back limit:
Example: Lyman-alpha transition in hydrogen
In this example, the fine-structure corrections are ignored.
| Initial state
()
|
Initial energy perturbation | Final state
()
|
Final energy perturbation |
|---|---|---|---|
Intermediate field for j = 1/2
In the magnetic dipole approximation, the Hamiltonian which includes both the hyperfine and Zeeman interactions is
where is the hyperfine splitting (in Hz) at zero applied magnetic field, and are the Bohr magneton and nuclear magneton respectively, and are the electron and nuclear angular momentum operators and is the Landé g-factor:
In the case of weak magnetic fields, the Zeeman interaction can be treated as a perturbation to the basis. In the high field regime, the magnetic field becomes so strong that the Zeeman effect will dominate, and one must use a more complete basis of or just since and will be constant within a given level.
To get the complete picture, including intermediate field strengths, we must consider eigenstates which are superpositions of the and basis states. For , the Hamiltonian can be solved analytically, resulting in the Breit–Rabi formula (named after Gregory Breit and Isidor Isaac Rabi). Notably, the electric quadrupole interaction is zero for (), so this formula is fairly accurate.
We now utilize quantum mechanical ladder operators, which are defined for a general angular momentum operator as
These ladder operators have the property
as long as lies in the range (otherwise, they return zero). Using ladder operators and We can rewrite the Hamiltonian as
We can now see that at all times, the total angular momentum projection will be conserved. This is because both and leave states with definite and unchanged, while and either increase and decrease or vice versa, so the sum is always unaffected. Furthermore, since there are only two possible values of which are . Therefore, for every value of there are only two possible states, and we can define them as the basis:
This pair of states is a two-level quantum mechanical system. Now we can determine the matrix elements of the Hamiltonian:
Solving for the eigenvalues of this matrix – as can be done by hand (see two-level quantum mechanical system), or more easily, with a computer algebra system – we arrive at the energy shifts:
where is the splitting (in units of Hz) between two hyperfine sublevels in the absence of magnetic field , is referred to as the 'field strength parameter' (Note: for the expression under the square root is an exact square, and so the last term should be replaced by ). This equation is known as the Breit–Rabi formula and is useful for systems with one valence electron in an () level.
Note that index in should be considered not as total angular momentum of the atom but as asymptotic total angular momentum. It is equal to total angular momentum only if otherwise eigenvectors corresponding different eigenvalues of the Hamiltonian are the superpositions of states with different but equal (the only exceptions are ).
Applications
Astrophysics

George Ellery Hale was the first to notice the Zeeman effect in the solar spectra, indicating the existence of strong magnetic fields in sunspots. Such fields can be quite high, on the order of 0.1 tesla or higher. Today, the Zeeman effect is used to produce magnetograms showing the variation of magnetic field on the Sun, and to analyse the magnetic field geometries in other stars.
Laser cooling
The Zeeman effect is utilized in many laser cooling applications such as a magneto-optical trap and the Zeeman slower.
Spintronics
Zeeman-energy mediated coupling of spin and orbital motions is used in spintronics for controlling electron spins in quantum dots through electric dipole spin resonance.
Metrology
Old high-precision frequency standards, i.e. hyperfine structure transition-based atomic clocks, may require periodic fine-tuning due to exposure to magnetic fields. This is carried out by measuring the Zeeman effect on specific hyperfine structure transition levels of the source element (cesium) and applying a uniformly precise, low-strength magnetic field to said source, in a process known as degaussing.
The Zeeman effect may also be utilized to improve accuracy in atomic absorption spectroscopy.
Biology
A theory about the magnetic sense of birds assumes that a protein in the retina is changed due to the Zeeman effect.
Nuclear spectroscopy
The nuclear Zeeman effect is important in such applications as nuclear magnetic resonance spectroscopy, magnetic resonance imaging (MRI), and Mössbauer spectroscopy.
Other
The electron spin resonance spectroscopy is based on the Zeeman effect.
Demonstrations

The Zeeman effect can be demonstrated by placing a sodium vapor source in a powerful electromagnet and viewing a sodium vapor lamp through the magnet opening (see diagram). With magnet off, the sodium vapor source will block the lamp light; when the magnet is turned on the lamp light will be visible through the vapor.
The sodium vapor can be created by sealing sodium metal in an evacuated glass tube and heating it while the tube is in the magnet.
Alternatively, salt (sodium chloride) on a ceramic stick can be placed in the flame of Bunsen burner as the sodium vapor source. When the magnetic field is energized, the lamp image will be brighter. However, the magnetic field also affects the flame, making the observation depend upon more than just the Zeeman effect. These issues also plagued Zeeman's original work; he devoted considerable effort to ensure his observations were truly an effect of magnetism on light emission.
When salt is added to the Bunsen burner, it dissociates to give sodium and chloride. The sodium atoms get excited due to photons from the sodium vapour lamp, with electrons excited from 3s to 3p states, absorbing light in the process. The sodium vapour lamp emits light at 589nm, which has precisely the energy to excite an electron of a sodium atom. If it was an atom of another element, like chlorine, shadow will not be formed. When a magnetic field is applied, due to the Zeeman effect the spectral line of sodium gets split into several components. This means the energy difference between the 3s and 3p atomic orbitals will change. As the sodium vapour lamp don't precisely deliver the right frequency any more, light doesn't get absorbed and passes through, resulting in the shadow dimming. As the magnetic field strength is increased, the shift in the spectral lines increases and lamp light is transmitted.
See also
- Magneto-optic Kerr effect
- Voigt effect
- Faraday effect
- Cotton–Mouton effect
- Polarization spectroscopy
- Zeeman energy
- Stark effect
- Lamb shift
References
- ^ Pais, Abraham (2002). Inward bound: of matter and forces in the physical world (Reprint ed.). Oxford: Clarendon Press ISBN 978-0-19-851997-3.
- Pieter, Zeeman (1902). "Pieter Zeeman Nobel Lecture". The Nobel Prize. Archived from the original on 15 November 2018. Retrieved 1 March 2024.
- Preston, Thomas (1898). "Radiation phenomena in a strong magnetic field". The Scientific Transactions of the Royal Dublin Society. 2nd series. 6: 385–391.
- "Niels Bohr's Times: In Physics, Philosophy, and Polity" By Abraham Pais, page 201
- Jenkins, Francis; White, Harvey (3 December 2001). Fundamentals of Optics (4 ed.). McGraw-Hill Education. ISBN 978-0-07-256191-3.
- Dunlap, Richard A. (1 December 2023). "Hyperfine interactions—part III: the magnetic dipole interaction and the nuclear Zeeman effect". The Mössbauer Effect (Second Edition). doi:10.1088/978-0-7503-6039-5ch7. ISBN 978-0-7503-6039-5. Retrieved 4 March 2024.
- Paschen, F.; Back, E. (1921). "Liniengruppen magnetisch vervollständigt" [Line groups magnetically completed ]. Physica (in German). 1: 261–273. Available at: Leiden University (Netherlands)
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. p. 280. ISBN 0-13-111892-7. OCLC 40251748.
- Woodgate, Gordon Kemble (1980). Elementary Atomic Structure (2nd ed.). Oxford, England: Oxford University Press. pp. 193–194.
- First appeared in: Breit, G.; Rabi, I.I. (1931). "Measurement of nuclear spin". Physical Review. 38 (11): 2082–2083. Bibcode:1931PhRv...38.2082B. doi:10.1103/PhysRev.38.2082.2.
- Kochukhov, Oleg (December 2021). "Magnetic fields of M dwarfs". The Astronomy and Astrophysics Review. 29 (1): 1. arXiv:2011.01781. doi:10.1007/s00159-020-00130-3. ISSN 0935-4956.
- Y. Tokura, W. G. van der Wiel, T. Obata, and S. Tarucha, Coherent single electron spin control in a slanting Zeeman field, Phys. Rev. Lett. 96, 047202 (2006)
- Verdiell, Marc (CuriousMarc) (31 October 2022). How an Atomic Clock Really Works, Round 2: Zeeman Alignment (YouTube video). Retrieved 11 March 2023.
- Thalau, Peter; Ritz, Thorsten; Burda, Hynek; Wegner, Regina E.; Wiltschko, Roswitha (18 April 2006). "The magnetic compass mechanisms of birds and rodents are based on different physical principles". Journal of the Royal Society Interface. 3 (9): 583–587. doi:10.1098/rsif.2006.0130. PMC 1664646. PMID 16849254.
- ^ Candle flame is repelled by magnets (and Zeeman follow-up), retrieved 27 February 2024
- Candle flame is repelled by magnets (and Zeeman follow-up), retrieved 27 February 2024
- Kox, A J (1 May 1997). "The discovery of the electron: II. The Zeeman effect". European Journal of Physics. 18 (3): 139–144. Bibcode:1997EJPh...18..139K. doi:10.1088/0143-0807/18/3/003. ISSN 0143-0807. S2CID 53414643.
- Suzuki, Masatsugu Sei; Suzuki, Itsuko S. (2011). "Lecture Note on Senior Laboratory Zeeman effect in Na, Cd, and Hg". ResearchGate.
Historical
- Condon, E. U.; G. H. Shortley (1935). The Theory of Atomic Spectra. Cambridge University Press. ISBN 0-521-09209-4. (Chapter 16 provides a comprehensive treatment, as of 1935.)
- Zeeman, P. (1896). "Over de invloed eener magnetisatie op den aard van het door een stof uitgezonden licht" [On the influence of magnetism on the nature of the light emitted by a substance]. Verslagen van de Gewone Vergaderingen der Wis- en Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) (in Dutch). 5: 181–184 and 242–248. Bibcode:1896VMKAN...5..181Z.
- Zeeman, P. (1897). "On the influence of magnetism on the nature of the light emitted by a substance". Philosophical Magazine. 5th series. 43 (262): 226–239. doi:10.1080/14786449708620985.
- Zeeman, P. (11 February 1897). "The effect of magnetisation on the nature of light emitted by a substance". Nature. 55 (1424): 347. Bibcode:1897Natur..55..347Z. doi:10.1038/055347a0.
- Zeeman, P. (1897). "Over doubletten en tripletten in het spectrum, teweeggebracht door uitwendige magnetische krachten" [On doublets and triplets in the spectrum, caused by external magnetic forces]. Verslagen van de Gewone Vergaderingen der Wis- en Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) (in Dutch). 6: 13–18, 99–102, and 260–262.
- Zeeman, P. (1897). "Doublets and triplets in the spectrum produced by external magnetic forces". Philosophical Magazine. 5th series. 44 (266): 55–60. doi:10.1080/14786449708621028.
Modern
- Feynman, Richard; Leighton, Robert B.; Sands, Matthew (1989). The Feynman Lectures on Physics. Vol. 3. Addison-Wesley. ISBN 0-201-02115-3.
- Forman, Paul (1970). "Alfred Landé and the anomalous Zeeman Effect, 1919-1921". Historical Studies in the Physical Sciences. 2: 153–261. doi:10.2307/27757307. JSTOR 27757307.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Liboff, Richard L. (2002). Introductory Quantum Mechanics (4th ed.). Addison-Wesley. ISBN 0-8053-8714-5. OCLC 50475492.
- Sobelman, Igor I. (2006). Theory of Atomic Spectra. Alpha Science. ISBN 1-84265-203-6. OCLC 71825022.
- Foot, C.J. (2005). Atomic Physics. OUP Oxford. ISBN 0-19-850696-1. OCLC 57478010.

 is the unperturbed Hamiltonian of the atom, and
is the unperturbed Hamiltonian of the atom, and  is the
is the 
 is the
is the 
 is the
is the  is the total electronic
is the total electronic  is the
is the  and the
and the  , with each multiplied by the appropriate
, with each multiplied by the appropriate 
 and
and  (the latter is called the
(the latter is called the 
 is small (less than the
is small (less than the  is. The spin and orbital angular momentum vectors can be thought of as precessing about the (fixed) total angular momentum vector
is. The spin and orbital angular momentum vectors can be thought of as precessing about the (fixed) total angular momentum vector 


 and squaring both sides, we get
and squaring both sides, we get

 and squaring both sides, we get
and squaring both sides, we get

 , we obtain the magnetic potential energy of the atom in the applied external magnetic field,
, we obtain the magnetic potential energy of the atom in the applied external magnetic field,

 and
and  ) and
) and  is the z-component of the total angular momentum.
For a single electron above filled shells
is the z-component of the total angular momentum.
For a single electron above filled shells  and
and  , the Landé g-factor can be simplified into:
, the Landé g-factor can be simplified into:

 to be the perturbation, the Zeeman correction to the energy is
to be the perturbation, the Zeeman correction to the energy is

 and
and 
 ) and the 2P3/2 level into 4 states (
) and the 2P3/2 level into 4 states ( ). The Landé g-factors for the three levels are:
). The Landé g-factors for the three levels are:
 for
for  (j=1/2, l=0)
(j=1/2, l=0) for
for  (j=1/2, l=1)
(j=1/2, l=1) for
for  (j=3/2, l=1).
(j=3/2, l=1).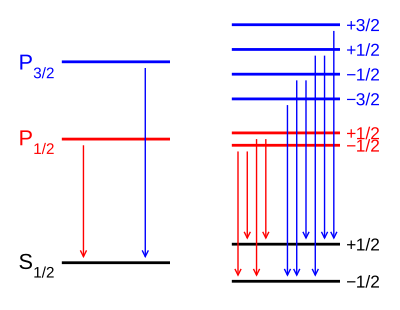
 )
)

 )
)









 , the two effects are equivalent. The effect was named after the
, the two effects are equivalent. The effect was named after the  . This allows the expectation values of
. This allows the expectation values of  and
and  to be easily evaluated for a state
to be easily evaluated for a state  . The energies are simply
. The energies are simply

 and
and  are still "good" quantum numbers. Together with the
are still "good" quantum numbers. Together with the  this allows to ignore the spin degree of freedom altogether. As a result, only three spectral lines will be visible, corresponding to the
this allows to ignore the spin degree of freedom altogether. As a result, only three spectral lines will be visible, corresponding to the  selection rule. The splitting
selection rule. The splitting  is independent of the unperturbed energies and electronic configurations of the levels being considered.
is independent of the unperturbed energies and electronic configurations of the levels being considered.
 , each of these three components is actually a group of several transitions due to the residual spin–orbit coupling and relativistic corrections (which are of the same order, known as 'fine structure'). The first-order perturbation theory with these corrections yields the following formula for the hydrogen atom in the Paschen–Back limit:
, each of these three components is actually a group of several transitions due to the residual spin–orbit coupling and relativistic corrections (which are of the same order, known as 'fine structure'). The first-order perturbation theory with these corrections yields the following formula for the hydrogen atom in the Paschen–Back limit:















 is the hyperfine splitting (in Hz) at zero applied magnetic field,
is the hyperfine splitting (in Hz) at zero applied magnetic field,  are the
are the  are the electron and nuclear angular momentum operators and
are the electron and nuclear angular momentum operators and  is the
is the 
 basis. In the high field regime, the magnetic field becomes so strong that the Zeeman effect will dominate, and one must use a more complete basis of
basis. In the high field regime, the magnetic field becomes so strong that the Zeeman effect will dominate, and one must use a more complete basis of  or just
or just  since
since  and
and  will be constant within a given level.
will be constant within a given level.
 and
and  , the Hamiltonian can be solved analytically, resulting in the Breit–Rabi formula (named after
, the Hamiltonian can be solved analytically, resulting in the Breit–Rabi formula (named after  (
( as
as


 lies in the range
lies in the range  (otherwise, they return zero). Using ladder operators
(otherwise, they return zero). Using ladder operators  and
and  We can rewrite the Hamiltonian as
We can rewrite the Hamiltonian as

 will be conserved. This is because both
will be conserved. This is because both  and
and  leave states with definite
leave states with definite  and
and  unchanged, while
unchanged, while  and
and  either increase
either increase  . Therefore, for every value of
. Therefore, for every value of  there are only two possible states, and we can define them as the basis:
there are only two possible states, and we can define them as the basis:





 is the splitting (in units of Hz) between two hyperfine sublevels in the absence of magnetic field
is the splitting (in units of Hz) between two hyperfine sublevels in the absence of magnetic field  ,
,
 is referred to as the 'field strength parameter' (Note: for
is referred to as the 'field strength parameter' (Note: for  the expression under the square root is an exact square, and so the last term should be replaced by
the expression under the square root is an exact square, and so the last term should be replaced by  ). This equation is known as the Breit–Rabi formula and is useful for systems with one valence electron in an
). This equation is known as the Breit–Rabi formula and is useful for systems with one valence electron in an  (
( in
in  should be considered not as total angular momentum of the atom but as asymptotic total angular momentum. It is equal to total angular momentum only if
should be considered not as total angular momentum of the atom but as asymptotic total angular momentum. It is equal to total angular momentum only if  otherwise eigenvectors corresponding different eigenvalues of the Hamiltonian are the superpositions of states with different
otherwise eigenvectors corresponding different eigenvalues of the Hamiltonian are the superpositions of states with different  ).
).