 Lightning discharge bolts showing electromagnetically pinched plasma filaments
Lightning discharge bolts showing electromagnetically pinched plasma filaments A 1905 study of pinches, where electric lightning was used to create a Z-pinch inside a metal tube.
A 1905 study of pinches, where electric lightning was used to create a Z-pinch inside a metal tube. A current-driven toroidal Z-pinch in a krypton plasma
A current-driven toroidal Z-pinch in a krypton plasma
A pinch (or: Bennett pinch (after Willard Harrison Bennett), electromagnetic pinch, magnetic pinch, pinch effect, or plasma pinch.) is the compression of an electrically conducting filament by magnetic forces, or a device that does such. The conductor is usually a plasma, but could also be a solid or liquid metal. Pinches were the first type of device used for experiments in controlled nuclear fusion power.
Pinches occur naturally in electrical discharges such as lightning bolts, planetary auroras, current sheets, and solar flares.
Basic mechanism
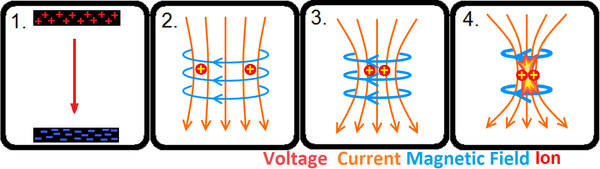
Types

Pinches exist in nature and in laboratories. Pinches differ in their geometry and operating forces. These include:
- Uncontrolled – Any time an electric current moves in large amounts (e.g., lightning, arcs, sparks, discharges) a magnetic force can pull together plasma. This can be insufficient for fusion.
- Sheet pinch – An astrophysical effect, this arises from vast sheets of charged particles.
- Z-pinch – The current runs down the axis, or walls, of a cylinder while the magnetic field is azimuthal
- Theta pinch – The magnetic field runs down the axis of a cylinder, while the electric field is in the azimuthal direction (also called a thetatron)
- Screw pinch – A combination of a Z-pinch and theta pinch (also called a stabilized Z-pinch, or θ-Z pinch)
- Reversed field pinch or toroidal pinch – This is a Z-pinch arranged in the shape of a torus. The plasma has an internal magnetic field. As distance increases from the center of this ring, the magnetic field reverses direction.
- Inverse pinch – An early fusion concept, this device consisted of a rod surrounded by plasma. Current traveled through the plasma and returned along the center rod. This geometry was slightly different than a z-pinch in that the conductor was in the center, not the sides.
- Cylindrical pinch
- Orthogonal pinch effect
- Ware pinch – A pinch that occurs inside a Tokamak plasma, when particles inside the banana orbit condense together.
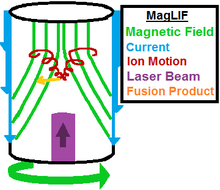
- Magnetized liner inertial fusion (MagLIF) – A Z-pinch of preheated, premagnetized fuel inside a metal liner, which could lead to ignition and practical fusion energy with a larger pulsed-power driver.
Common behavior
Pinches may become unstable. They radiate energy across the whole electromagnetic spectrum including radio waves, microwaves, infrared, x-rays, gamma rays, synchrotron radiation, and visible light. They also produce neutrons, as a product of fusion.

Applications and devices
Pinches are used to generate X-rays and the intense magnetic fields generated are used in electromagnetic forming of metals. They also have applications in particle beams including particle beam weapons, astrophysics studies and it has been proposed to use them in space propulsion. A number of large pinch machines have been built to study fusion power; here are several:
- MAGPIE A Z-pinch at Imperial College. This dumps a large amount of current across a wire. Under these conditions, the wire becomes plasma and compresses to produce fusion.
- Z Pulsed Power Facility at Sandia National Laboratories.
- ZETA device in Culham, England
- Madison Symmetric Torus at the University of Wisconsin, Madison
- Reversed-Field eXperiment in Italy.
- Dense plasma focus in New Jersey
- University of Nevada, Reno (USA)
- Cornell University (USA)
- University of Michigan (USA)
- University of California, San Diego (USA)
- University of Washington (USA)
- Ruhr University (Germany)
- École Polytechnique (France)
- Weizmann Institute of Science (Israel)
- Universidad Autónoma Metropolitana (Mexico).
- Zap Energy Inc. (USA)
Crushing cans with the pinch effect

Many high-voltage electronics enthusiasts make their own crude electromagnetic forming devices. They use pulsed power techniques to produce a theta pinch able to crush an aluminium soft drink can using the Lorentz forces created when large currents are induced in the can by the strong magnetic field of the primary coil.
An electromagnetic aluminium can crusher consists of four main components: a high-voltage DC power supply, which provides a source of electrical energy, a large energy discharge capacitor to accumulate the electrical energy, a high voltage switch or spark gap, and a robust coil (capable of surviving high magnetic pressure) through which the stored electrical energy can be quickly discharged in order to generate a correspondingly strong pinching magnetic field (see diagram below).

In practice, such a device is somewhat more sophisticated than the schematic diagram suggests, including electrical components that control the current in order to maximize the resulting pinch, and to ensure that the device works safely. For more details, see the notes.
History

The first creation of a Z-pinch in the laboratory may have occurred in 1790 in Holland when Martinus van Marum created an explosion by discharging 100 Leyden jars into a wire. The phenomenon was not understood until 1905, when Pollock and Barraclough investigated a compressed and distorted length of copper tube from a lightning rod after it had been struck by lightning. Their analysis showed that the forces due to the interaction of the large current flow with its own magnetic field could have caused the compression and distortion. A similar, and apparently independent, theoretical analysis of the pinch effect in liquid metals was published by Northrup in 1907. The next major development was the publication in 1934 of an analysis of the radial pressure balance in a static Z-pinch by Bennett (see the following section for details).
Thereafter, the experimental and theoretical progress on pinches was driven by fusion power research. In their article on the "Wire-array Z-pinch: a powerful x-ray source for ICF", M G Haines et al., wrote on the "Early history of Z-pinches".
- In 1946 Thompson and Blackman submitted a patent for a fusion reactor based on a toroidal Z-pinch with an additional vertical magnetic field. But in 1954 Kruskal and Schwarzschild published their theory of MHD instabilities in a Z-pinch. In 1956, Kurchatov gave his famous Harwell lecture showing nonthermal neutrons and the presence of m = 0 and m = 1 instabilities in a deuterium pinch. In 1957 Pease and Braginskii independently predicted radiative collapse in a Z-pinch under pressure balance when in hydrogen the current exceeds 1.4 MA. (The viscous rather than resistive dissipation of magnetic energy discussed above and in would however prevent radiative collapse).
In 1958, the world's first controlled thermonuclear fusion experiment was accomplished using a theta-pinch machine named Scylla I at the Los Alamos National Laboratory. A cylinder full of deuterium was converted into a plasma and compressed to 15 million degrees Celsius under a theta-pinch effect. Lastly, at Imperial College in 1960, led by R Latham, the Plateau–Rayleigh instability was shown, and its growth rate measured in a dynamic Z-pinch.
Equilibrium analysis
One dimension
In plasma physics three pinch geometries are commonly studied: the θ-pinch, the Z-pinch, and the screw pinch. These are cylindrically shaped. The cylinder is symmetric in the axial (z) direction and the azimuthal (θ) directions. The one-dimensional pinches are named for the direction the current travels.
The θ-pinch
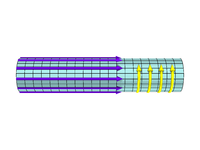
The θ-pinch has a magnetic field directed in the z direction and a large diamagnetic current directed in the θ direction. Using Ampère's circuital law (discarding the displacement term)
Since B is only a function of r we can simplify this to
So J points in the θ direction.
Thus, the equilibrium condition () for the θ-pinch reads:
θ-pinches tend to be resistant to plasma instabilities; This is due in part to Alfvén's theorem (also known as the frozen-in flux theorem).
The Z-pinch
Main article: Z-pinch
The Z-pinch has a magnetic field in the θ direction and a current J flowing in the z direction. Again, by electrostatic Ampère's law,
Thus, the equilibrium condition, , for the Z-pinch reads:
Although Z-pinches satisfy the MHD equilibrium condition, it is important to note that this is an unstable equilibrium, resulting in various instabilies such as the m = 0 instability ('sausage'), m = 1 instability ('kink'), and various other higher order instabilities.
The screw pinch
The screw pinch is an effort to combine the stability aspects of the θ-pinch and the confinement aspects of the Z-pinch. Referring once again to Ampère's law,
But this time, the B field has a θ component and a z component
So this time J has a component in the z direction and a component in the θ direction.
Finally, the equilibrium condition () for the screw pinch reads:
The screw pinch via colliding optical vortices
The screw pinch might be produced in laser plasma by colliding optical vortices of ultrashort duration. For this purpose optical vortices should be phase-conjugated. The magnetic field distribution is given here again via Ampère's law:
Two dimensions
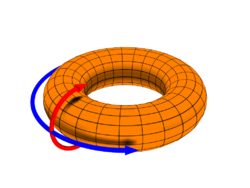
A common problem with one-dimensional pinches is the end losses. Most of the motion of particles is along the magnetic field. With the θ-pinch and the screw-pinch, this leads particles out of the end of the machine very quickly, leading to a loss of mass and energy. Along with this problem, the Z-pinch has major stability problems. Though particles can be reflected to some extent with magnetic mirrors, even these allow many particles to pass. A common method of beating these end losses, is to bend the cylinder around into a torus. Unfortunately this breaks θ symmetry, as paths on the inner portion (inboard side) of the torus are shorter than similar paths on the outer portion (outboard side). Thus, a new theory is needed. This gives rise to the famous Grad–Shafranov equation. Numerical solutions to the Grad–Shafranov equation have also yielded some equilibria, most notably that of the reversed field pinch.
Three dimensions
As of 2015, there is no coherent analytical theory for three-dimensional equilibria. The general approach to finding such equilibria is to solve the vacuum ideal MHD equations. Numerical solutions have yielded designs for stellarators. Some machines take advantage of simplification techniques such as helical symmetry (for example University of Wisconsin's Helically Symmetric eXperiment). However, for an arbitrary three-dimensional configuration, an equilibrium relation, similar to that of the 1-D configurations exists:
Where κ is the curvature vector defined as:
with b the unit vector tangent to B.
Formal treatment

The Bennett relation
Consider a cylindrical column of fully ionized quasineutral plasma, with an axial electric field, producing an axial current density, j, and associated azimuthal magnetic field, B. As the current flows through its own magnetic field, a pinch is generated with an inward radial force density of j x B. In a steady state with forces balancing:
where ∇p is the magnetic pressure gradient, and pe and pi are the electron and ion pressures, respectively. Then using Maxwell's equation and the ideal gas law , we derive:
- (the Bennett relation)
where N is the number of electrons per unit length along the axis, Te and Ti are the electron and ion temperatures, I is the total beam current, and k is the Boltzmann constant.
The generalized Bennett relation
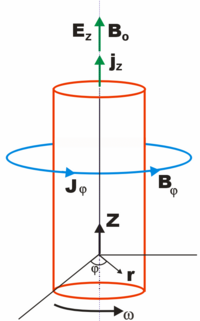
The generalized Bennett relation considers a current-carrying magnetic-field-aligned cylindrical plasma pinch undergoing rotation at angular frequency ω. Along the axis of the plasma cylinder flows a current density jz, resulting in an azimuthal magnetic field Βφ. Originally derived by Witalis, the generalized Bennett relation results in:
- where a current-carrying, magnetic-field-aligned cylindrical plasma has a radius a,
- J0 is the total moment of inertia with respect to the z axis,
- W⊥kin is the kinetic energy per unit length due to beam motion transverse to the beam axis
- WBz is the self-consistent Bz energy per unit length
- WEz is the self-consistent Ez energy per unit length
- Wk is thermokinetic energy per unit length
- I(a) is the axial current inside the radius a (r in diagram)
- N(a) is the total number of particles per unit length
- Er is the radial electric field
- Eφ is the rotational electric field
The positive terms in the equation are expansional forces while the negative terms represent beam compressional forces.
The Carlqvist relation
The Carlqvist relation, published by Per Carlqvist in 1988, is a specialization of the generalized Bennett relation (above), for the case that the kinetic pressure is much smaller at the border of the pinch than in the inner parts. It takes the form
and is applicable to many space plasmas.

The Carlqvist relation can be illustrated (see right), showing the total current (I) versus the number of particles per unit length (N) in a Bennett pinch. The chart illustrates four physically distinct regions. The plasma temperature is quite cold (Ti = Te = Tn = 20 K), containing mainly hydrogen with a mean particle mass 3×10 kg. The thermokinetic energy Wk >> πa pk(a). The curves, ΔWBz show different amounts of excess magnetic energy per unit length due to the axial magnetic field Bz. The plasma is assumed to be non-rotational, and the kinetic pressure at the edges is much smaller than inside.
Chart regions: (a) In the top-left region, the pinching force dominates. (b) Towards the bottom, outward kinetic pressures balance inwards magnetic pressure, and the total pressure is constant. (c) To the right of the vertical line ΔWBz = 0, the magnetic pressures balances the gravitational pressure, and the pinching force is negligible. (d) To the left of the sloping curve ΔWBz = 0, the gravitational force is negligible. Note that the chart shows a special case of the Carlqvist relation, and if it is replaced by the more general Bennett relation, then the designated regions of the chart are not valid.
Carlqvist further notes that by using the relations above, and a derivative, it is possible to describe the Bennett pinch, the Jeans criterion (for gravitational instability, in one and two dimensions), force-free magnetic fields, gravitationally balanced magnetic pressures, and continuous transitions between these states.
References in culture
A fictionalized pinch-generating device was used in Ocean's Eleven, where it was used to disrupt Las Vegas's power grid just long enough for the characters to begin their heist.
See also
- Electromagnetic forming
- Explosively pumped flux compression generator
- Fusion power
- Madison Symmetric Torus (reversed field pinch)
References
- ^ Pollock J A and Barraclough S (1905) Proc. R. Soc. New South Wales 39 131
- Buneman, O. (1961). "The Bennett Pinch". In Drummond, James E. (ed.). Plasma Physics. New York: McGraw-Hill. p. 202. Bibcode:1961plph.conf..202B. LOC 60-12766.
- Lee, S. (1983). "Energy balance and the radius of electromagnetically pinched plasma columns". Plasma Physics. 25 (5): 571–576. Bibcode:1983PlPh...25..571L. doi:10.1088/0032-1028/25/5/009.
- Schmidt, Helmut (1966). "Formation of a Magnetic Pinch in InSb and the Possibility of Population Inversion in the Pinch". Physical Review. 149 (2): 564–573. Bibcode:1966PhRv..149..564S. doi:10.1103/physrev.149.564.
- Severnyi, A. B. (1959). "On the Appearance of Cosmics Rays in the Pinch Effect in Solar Flares". Soviet Astronomy. 3: 887. Bibcode:1959SvA.....3..887S.
- Zueva, N. M.; Solov'ev, L. S.; Morozov, A. I. (1976). "Nonlinear instability of plasma pinches". Journal of Experimental and Theoretical Physics Letters. 23: 256. Bibcode:1976JETPL..23..256Z.
- ^ Phillips, James (Winter 1983). "Magnetic Fusion". Los Alamos Science. pp. 64–67.
- Rai, J.; Singh, A. K.; Saha, S. K (1973). "Magnetic field within the return stroke channel of lightning". Indian Journal of Radio and Space Physics. 2: 240–242. Bibcode:1973IJRSP...2..240R.
- Galperin, Iu. I.; Zelenyi, L. M.; Kuznetsova, M. M. (1986). "Pinching of field-aligned currents as a possible mechanism for the formation of raylike auroral forms". Kosmicheskie Issledovaniia. 24: 865–874. Bibcode:1986KosIs..24..865G.
- Syrovatskii, S. I. (1981). "Pinch sheets and reconnection in astrophysics". Annual Review of Astronomy and Astrophysics. 19: 163–229. Bibcode:1981ARA&A..19..163S. doi:10.1146/annurev.aa.19.090181.001115.
- Airapetyan, V. S.; Vikhrev, V. V.; Ivanov, V. V.; Rozanova, G. A. (1990). "Pinch Mechanism of Energy Release of Stellar Flares". Astrophysics. 32 (3): 230–235. Bibcode:1990Ap.....32..230A. doi:10.1007/bf01005504. S2CID 120883355.
- ^ Carlqvist, Per (May 1988). "Cosmic electric currents and the generalized Bennett relation". Astrophysics and Space Science. 144 (1–2): 73–84. Bibcode:1988Ap&SS.144...73C. doi:10.1007/BF00793173. S2CID 119719745.
- Biskamp, Dieter (1997). Nonlinear Magnetohydrodynamics. Cambridge, England: Cambridge University Press. p. 130. ISBN 0-521-59918-0.
- Basu, Dipak K. (8 October 2018). Dictionary of Material Science and High Energy Physics. CRC Press. p. 315. ISBN 978-0-8493-2889-3.
- Srivastava, K. M.; Vyas, D. N. (August 1982). "Non-linear analysis of the stability of the screw pinch". Astrophysics and Space Science. 86 (1): 71–89. Bibcode:1982Ap&SS..86...71S. doi:10.1007/BF00651831. S2CID 121575638.
- See "MHD Equilibria" in Introduction to Plasma Physics by I.H.Hutchinson (2001)
- Srivastava, K. M.; Waelbroeck, F. (1976). "On the stability of the screw pinch in the CGL model". Journal of Plasma Physics. 16 (3): 261. Bibcode:1976JPlPh..16..261S. doi:10.1017/s0022377800020201. S2CID 123689314.
- Anderson, O. A.; Furth, H. P.; Stone, J. M.; Wright, R. E. (November 1958). "Inverse Pinch Effect". Physics of Fluids. 1 (6): 489–494. Bibcode:1958PhFl....1..489A. doi:10.1063/1.1724372.
- Helander, P.; Akers, R. J.; Valovič, M. (3 November 2005). "The effect of non-inductive current drive on tokamak transport". Plasma Physics and Controlled Fusion. 47 (12B): B151 – B163. Bibcode:2005PPCF...47B.151H. doi:10.1088/0741-3335/47/12b/s12. S2CID 121961613.
- Nishikawa, K.; Wakatani, M. (2000-01-24). Plasma Physics: Third Edition. Springer Science & Business Media. ISBN 978-3-540-65285-4.
- Slutz, Stephen; Vesey, Roger A. (2012). "High-Gain Magnetized Inertial Fusion". Physical Review Letters. 108 (2): 025003. Bibcode:2012PhRvL.108b5003S. doi:10.1103/PhysRevLett.108.025003. PMID 22324693.
- Hardee, P. E. (1982). "Helical and pinching instability of supersonic expanding jets in extragalactic radio sources". Astrophysical Journal. 257: 509–526. Bibcode:1982ApJ...257..509H. doi:10.1086/160008.
- Pereira, N. R.; et al. (1988). "X-rays from Z-pinches on relativistic electron-beam generators". Journal of Applied Physics. 64 (3): R1 – R27. Bibcode:1988JAP....64....1P. doi:10.1063/1.341808.
- Wu, Mei; Chen, Li; Li, Ti-Pei (2005). "Polarization in Gamma-Ray Bursts Produced by Pinch Discharge". Chinese Journal of Astronomy & Astrophysics. 5 (1): 57–64. arXiv:astro-ph/0501334. Bibcode:2005ChJAA...5...57W. doi:10.1088/1009-9271/5/1/007. S2CID 121943.
- Peratt, A.L., "Synchrotron radiation from pinched particle beams", (1998) Plasma Physics: VII Lawpp 97: Proceedings of the 1997 Latin American Workshop on Plasma Physics, Edited by Pablo Martin, Julio Puerta, Pablo Martmn, with reference to Meierovich, B. E., "Electromagnetic collapse. Problems of stability, emission of radiation and evolution of a dense pinch" (1984) Physics Reports, Volume 104, Issue 5, p. 259-346.
- Anderson, Oscar A.; et al. (1958). "Neutron Production in Linear Deuterium Pinches". Physical Review. 110 (6): 1375–1387. Bibcode:1958PhRv..110.1375A. doi:10.1103/physrev.110.1375.
- Ryutov, D. D.; Derzon, M. S.; Matzen, M. K (2000). "The physics of fast Z pinches". Reviews of Modern Physics. 72 (1): 167–223. Bibcode:2000RvMP...72..167R. doi:10.1103/revmodphys.72.167.
- Andre Gsponer, "Physics of high-intensity high-energy particle beam propagation in open air and outer-space plasmas" (2004) https://arxiv.org/abs/physics/0409157
- Peratt, Anthony L., "The role of particle beams and electrical currents in the plasma universe" (1988) Laser and Particle Beams (ISSN 0263-0346), vol. 6, Aug. 1988, p. 471-491.
- "Z-Pinch Pulsed Plasma Propulsion Technology Development" Final Report Advanced Concepts Office (ED04) Marshall Space Flight Center October 8, 2010, Tara Polsgrove, Et Al.
- http://dorland.pp.ph.ic.ac.uk/magpie/?page_id=239 Archived 2014-11-05 at the Wayback Machine "Wire Arrays Z-Pinch" accessed: 3-27-2015
- LaPointe, Robert. "High Voltage Devices and Experiments". Retrieved February 21, 2013.
- Tristan. "Electromagnetic Can Crusher". Retrieved February 21, 2013.
- Borros, Sam. "Solid State Can Crusher". Retrieved February 21, 2013.
- "MagnetoPulS". Magnet-Physik, Dr. Steingroever GmbH. 2002. Archived from the original on 2003-05-22. Retrieved February 21, 2013.
- "Industrial Application of the Electromagnetic Pulse Technology" (PDF). white paper. PSTproducts GmbH. June 2009. Archived from the original (PDF) on July 15, 2011. Retrieved February 21, 2013.
- Examples of electromagnetic pinch can crushers can be found at (a) Bob LaPointe's site on High Voltage Devices and Experiments (b) Tristran's Electromagnetic Can Crusher (including schematic) (c) Sam Borros's Solid State Can Crusher
- See also the IEEE History Center, "Evolution of the IEEE Logo" March 1963; see also the comments in "Laboratory Astrophysics"
- van Marum M 1790 Proc. 4th Int. Conf. on Dense Z-Pinches (Vancouver 1997) (Am. Inst. Phys. Woodbury, New York, 1997) Frontispiece and p ii
- R. S. Pease, "The Electromagnetic Pinch: From Pollock to the Joint European Torus", "Pollock Memorial Lecture for 1984 delivered at the University of Sydney, 28 November, 1984" Archived 2006-05-29 at the Wayback Machine
- Northrup, Edwin F. (1907). "Some Newly Observed Manifestations of Forces in the Interior of an Electric Conductor". Physical Review. Series I. 24 (6). American Physical Society (APS): 474–497. Bibcode:1907PhRvI..24..474N. doi:10.1103/physrevseriesi.24.474. ISSN 1536-6065.
- Bennett, Willard H. (1934). "Magnetically Self-Focussing Streams". Phys. Rev. 45 (12): 890–897. Bibcode:1934PhRv...45..890B. doi:10.1103/physrev.45.890.
- Haines, M G; Sanford, T W L; Smirnov, V P (2005). "Wire-array Z-pinch: a powerful x-ray source for ICF". Plasma Phys. Control. Fusion. 47 (12B): B1 – B11. Bibcode:2005PPCF...47B...1H. doi:10.1088/0741-3335/47/12b/s01. S2CID 120320797.
- Thompson, G. P.; Blackman; Haines, M. G. (1996). "Historical Perspective: Fifty years of controlled fusion research". Plasma Physics and Controlled Fusion. 38 (5): 643–656. Bibcode:1996PPCF...38..643H. doi:10.1088/0741-3335/38/5/001. S2CID 250763028.
- Kruskal, M D; Schwarzschild (1954). "Some Instabilities of a Completely Ionized Plasma". Proc. R. Soc. Lond. A. 223 (1154): 348–360. Bibcode:1954RSPSA.223..348K. doi:10.1098/rspa.1954.0120. S2CID 121125652.
- Kurchatov I V (1957) J. Nucl. Energy 4 193
- Pease, R S (1957). "Equilibrium Characteristics of a Pinched Gas Discharge Cooled by Bremsstrahlung Radiation". Proc. Phys. Soc. Lond. 70 (1): 11–23. Bibcode:1957PPSB...70...11P. doi:10.1088/0370-1301/70/1/304.
- Braginskii S I 1957 Zh. Eksp. Teor. Fiz 33 645
- Braginskii S I 1958 Sov. Phys.—JETP 6 494
- Haines M G et al. 2005 Phys. Rev. Lett.. submitted; see also EPS Conf. on Plasma Physics 2004 (London, UK) paper 73
- Curzon, F. L.; et al. (1960). "Experiments on the Growth Rate of Surface Instabilities in a Linear Pinched Discharge". Proc. R. Soc. Lond. A. 257 (1290): 386–401. Bibcode:1960RSPSA.257..386C. doi:10.1098/rspa.1960.0158. S2CID 96283997.
- Bellan, P. Fundamentals of Plasma Physics
- A.Yu.Okulov. "Laser singular Theta-pinch", Phys.Lett.A, v.374, 4523-4527, (2010)
- Optical phase conjugation and electromagnetic momenta
- Ideal Magnetohydrodynamics: Modern perspectives in energy. Jeffrey P. Freidberg. Massachusetts Institute of Technology. Cambridge, Massachusetts. Plenum Press - New York and London - 1987. (Pg. 86, 95)
- Trubnikov, Boris A (1992). "A new hypothesis of cosmic ray generation in plasma pinches". IEEE Transactions on Plasma Science. 20 (6): 898–904. Bibcode:1992ITPS...20..898T. doi:10.1109/27.199547.
- "The PLASMAK Configuration and Ball Lightning" (PDF Archived 2006-07-15 at the Wayback Machine) presented at the International Symposium on Ball Lightning; July 1988
- Witalis, E. A. "Plasma-physical aspects of charged-particle beams" (1981) Physical Review A - General Physics, 3rd Series, vol. 24, Nov. 1981, p. 2758–2764
- Anthony L . Peratt, "Physics of the Plasma Universe", 1992 Springer-Verlag, ISBN 0-387-97575-6
- Jeans, J. H. (1902). "The stability of a spherical nebula". Phil. Trans. R. Soc. Lond. A. 199 (312–320): 1–53. Bibcode:1902RSPTA.199....1J. doi:10.1098/rsta.1902.0012.
- "The Con-Artist Physics of 'Ocean's Eleven'". American Physical Society. March 2002.
External links
- Examples of electromagnetically shrunken coins and crushed cans
- Theory of electromagnetic coin shrinking
- The Known History of "Quarter Shrinking"
- Can crushing info using electromagnetism among other things
- The MAGPIE project at Imperial College London is used to study wire array Z-pinch implosions.


 ) for the θ-pinch reads:
) for the θ-pinch reads:









 and the
and the  , we derive:
, we derive:
 (the Bennett relation)
(the Bennett relation)
