| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Lake retention time" – news · newspapers · books · scholar · JSTOR (August 2024) (Learn how and when to remove this message) |
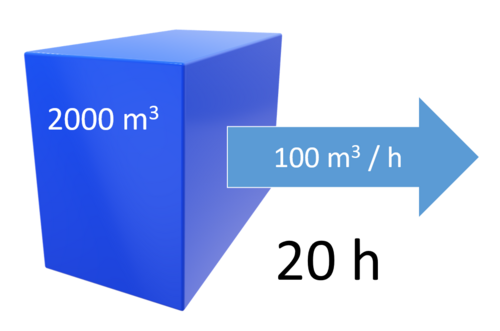
Lake retention time (also called the residence time of lake water, or the water age or flushing time) is a calculated quantity expressing the mean time that water (or some dissolved substance) spends in a particular lake. At its simplest, this figure is the result of dividing the lake volume by the flow in or out of the lake. It roughly expresses the amount of time taken for a substance introduced into a lake to flow out of it again. The retention time is particularly important where downstream flooding or pollutants are concerned.
Global retention time
The global retention time for a lake (the overall mean time that water spends in the lake) is calculated by dividing the lake volume by either the mean rate of inflow of all tributaries, or by the mean rate of outflow (ideally including evaporation and seepage). This metric assumes that water in the lake is well-mixed (rather than stratified), so that any portion of the lake water is much like any other. In reality, larger and deeper lakes are generally not well-mixed. Many large lakes can be divided into distinct portions with only limited flow between them. Deep lakes are generally stratified, with deeper water mixing infrequently with surface water. These are often better modeled as several distinct sub-volumes of water.
More specific residence times
It is possible to calculate more specific residence time figures for a particular lake, such as individual residence times for sub-volumes (e.g. particular arms), or a residence time distribution for the various layers of a stratified lake. These figures can often better express the hydrodynamics of the lake. However, any such approach remains a simplification and must be guided by an understanding of the processes operating in the lake.
Two approaches can be used (often in combination) to elucidate how a particular lake works: field measurements and mathematical modeling. One common technique for field measurement is to introduce a tracer into the lake and monitor its movement. This can be a solid tracer, such as a float constructed to be neutrally buoyant within a particular water layer, or sometimes a liquid. This approach is sometimes referred to as using a Lagrangian reference frame. Another field measurement approach, using an Eulerian reference frame, is to capture various properties of the lake water (including mass movement, water temperature, electrical conductivity and levels of dissolved substances, typically oxygen) at various fixed positions in the lake. From these can be constructed an understanding of the dominant processes operating in the various parts of the lake and their range and duration.
Field measurements alone are usually not a reliable basis for generating residence times, mainly because they necessarily represent a small subset of locations and conditions. Therefore, the measurements are generally used as the input for numerical models. In theory it would be possible to integrate a system of hydrodynamic equations with variable boundary conditions over a very long period sufficient for inflowing water particles to exit the lake. One could then calculate the traveling times of the particles using a Lagrangian method. However, this approach exceeds the detail available in current hydrodynamic models and the capacity of current computer resources. Instead, residence time models developed for gas and fluid dynamics, chemical engineering, and bio-hydrodynamics can be adapted to generate residence times for sub-volumes of lakes.
Renewal time
One useful mathematical model is the measurement of how quickly inflows are able to refill a lake. Renewal time is a specific measure of retention time, where the focus is on 'how long does it take to completely replace all water in a lake.' This is modeling can only be done with an accurate budget of all water gained and lost by the system. Renewal time simply becomes a question how quickly could the inflows of the lake fill the entire volume of the basin (this does still assume the outflows are unchanged). For example if Lake Michigan was emptied, it would take 99 years for its tributaries to completely refill the lake.
List of residence times of lake water
The residence time listed is taken from the infobox in the associated article unless otherwise specified.
See also
References
- ^ Duwe, Kurt (2003-01-03). "D24: Realistic Residence Times Studies" (PDF). Integrated Water Resource Management for Important Deep European Lakes and their Catchment Areas. EUROLAKES. Archived from the original (PDF) on January 26, 2007. Retrieved 2007-12-11.
- Wetzel, R. G. (2001). Limnology 3rd Edition. New York: Academic Press.
- "Poyang Lake". International Lake Environment Committee Foundation. Archived from the original on December 13, 2013. Retrieved February 13, 2014.
- Colman, John A and Paul J. Friesz. "Geohydrology and Limnology of Walden Pond, Concord, Massachusetts". USGS. Retrieved 2020-07-07.
Further reading
- Quinn, Frank H. (1992). "Hydraulic residence times for the Laurentian Great Lakes". Journal of Great Lakes Research. 18 (1): 22–28. Bibcode:1992JGLR...18...22Q. doi:10.1016/S0380-1330(92)71271-4.
External links
- EPA's Great Lakes Factsheet #1
- EPA's Great Lakes Atlas
- Jody Richardson, Alistair McKerchar (December 2006). "Land-locked fish and lake-residence time". Retrieved 22 May 2007. - relationship between residence time of lakes of New Zealand and koaro, smelt and common bully populations.