Rising sun lemma - Misplaced Pages

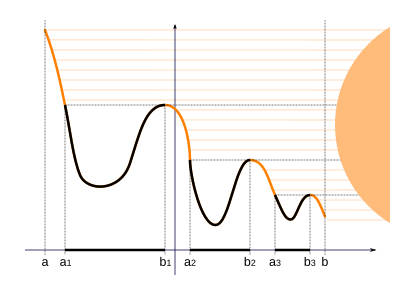
In mathematical analysis, the rising sun lemma is a lemma due to Frigyes Riesz, used in the proof of the Hardy–Littlewood maximal theorem. The lemma was a precursor in one dimension of the Calderón–Zygmund lemma.

The lemma is stated as follows:

Suppose g is a real-valued continuous function on the interval and S is the set of x in such that there exists a y∈(x,b] with g(y) > g(x). (Note that b cannot be in S, though a may be.) Define E = S ∩ (a,b).

Then E is an open set, and it may be written as a countable union of disjoint intervals

E=\bigcup _{k}(a_{k},b_{k})

such that g(a_k) = g(b_k), unless a_k = a ∈ S for some k, in which case g(a) < g(b_k) for that one k. Furthermore, if x ∈ (a_k,b_k), then g(x) < g(b_k).

The colorful name of the lemma comes from imagining the graph of the function g as a mountainous landscape, with the sun shining horizontally from the right. The set E consist of points that are in the shadow.

Proof

We need a lemma: Suppose [c,d) ⊂ S, but d ∉ S. Then g(c) < g(d). To prove this, suppose g(c) ≥ g(d). Then g achieves its maximum on at some point z < d. Since z ∈ S, there is a y in (z,b] with g(z) < g(y). If y ≤ d, then g would not reach its maximum on at z. Thus, y ∈ (d,b], and g(d) ≤ g(z) < g(y). This means that d ∈ S, which is a contradiction, thus establishing the lemma.

The set E is open, so it is composed of a countable union of disjoint intervals (a_k,b_k).

It follows immediately from the lemma that g(x) < g(b_k) for x in (a_k,b_k). Since g is continuous, we must also have g(a_k) ≤ g(b_k).

If a_k ≠ a or a ∉ S, then a_k ∉ S, so g(a_k) ≥ g(b_k), for otherwise a_k ∈ S. Thus, g(a_k) = g(b_k) in these cases.

Finally, if a_k = a ∈ S, the lemma tells us that g(a) < g(b_k).

Notes

Stein 1998
See:
- Riesz 1932
- Zygmund 1977, p. 31
- Tao 2011, pp. 118–119
- Duren 2000, Appendix B

References

Duren, Peter L. (2000), Theory of H Spaces, New York: Dover Publications, ISBN 0-486-41184-2
Garling, D.J.H. (2007), Inequalities: a journey into linear analysis, Cambridge University Press, ISBN 978-0-521-69973-0
Korenovskyy, A. A.; A. K. Lerner; A. M. Stokolos (November 2004), "On a multidimensional form of F. Riesz's "rising sun" lemma", Proceedings of the American Mathematical Society, 133 (5): 1437–1440, doi:10.1090/S0002-9939-04-07653-1
Riesz, Frédéric (1932), "Sur un Théorème de Maximum de Mm. Hardy et Littlewood", Journal of the London Mathematical Society, 7 (1): 10–13, doi:10.1112/jlms/s1-7.1.10, archived from the original on 2013-04-15, retrieved 2008-07-21
Stein, Elias (1998), "Singular integrals: The Roles of Calderón and Zygmund" (PDF), Notices of the American Mathematical Society, 45 (9): 1130–1140.
Tao, Terence (2011), An Introduction to Measure Theory, Graduate Studies in Mathematics, vol. 126, American Mathematical Society, ISBN 978-0821869192
Zygmund, Antoni (1977), Trigonometric Series. Vol. I, II (2nd ed.), Cambridge University Press, ISBN 0-521-07477-0

Categories: