| This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2018) (Learn how and when to remove this message) |

Limb darkening is an optical effect seen in stars (including the Sun) and planets, where the central part of the disk appears brighter than the edge, or limb. Its understanding offered early solar astronomers an opportunity to construct models with such gradients. This encouraged the development of the theory of radiative transfer.
Basic theory
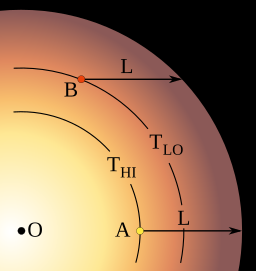
Optical depth, a measure of the opacity of an object or part of an object, combines with effective temperature gradients inside the star to produce limb darkening. The light seen is approximately the integral of all emission along the line of sight modulated by the optical depth to the viewer (i.e. 1/e times the emission at 1 optical depth, 1/e times the emission at 2 optical depths, etc.). Near the center of the star, optical depth is effectively infinite, causing approximately constant brightness. However, the effective optical depth decreases with increasing radius due to lower gas density and a shorter line of sight distance through the star, producing a gradual dimming, until it becomes zero at the apparent edge of the star.
The effective temperature of the photosphere also decreases with increasing distance from the center of the star. The radiation emitted from a gas is approximately black-body radiation, the intensity of which is proportional to the fourth power of the temperature. Therefore, even in line of sight directions where the optical depth is effectively infinite, the emitted energy comes from cooler parts of the photosphere, resulting in less total energy reaching the viewer.
The temperature in the atmosphere of a star does not always decrease with increasing height. For certain spectral lines, the optical depth is greatest in regions of increasing temperature. In this scenario, the phenomenon of "limb brightening" is seen instead. In the Sun, the existence of a temperature minimum region means that limb brightening should start to dominate at far-infrared or radio wavelengths. Above the lower atmosphere, and well above the temperature-minimum region, the Sun is surrounded by the million-kelvin solar corona. For most wavelengths this region is optically thin, i.e. has small optical depth, and must, therefore, be limb-brightened if it is spherically symmetric.
Calculation of limb darkening

In the figure shown here, as long as the observer at point P is outside the stellar atmosphere, the intensity seen in the direction θ will be a function only of the angle of incidence ψ. This is most conveniently approximated as a polynomial in cos ψ: where I(ψ) is the intensity seen at P along a line of sight forming angle ψ with respect to the stellar radius, and I(0) is the central intensity. In order that the ratio be unity for ψ = 0, we must have
For example, for a Lambertian radiator (no limb darkening) we will have all ak = 0 except a1 = 1. As another example, for the Sun at 550 nanometres (5.5×10 m), the limb darkening is well expressed by N = 2 and
The equation for limb darkening is sometimes more conveniently written as which now has N independent coefficients rather than N + 1 coefficients that must sum to unity.
The ak constants can be related to the Ak constants. For N = 2,
For the Sun at 550 nm, we then have
This model gives an intensity at the edge of the Sun's disk of only 30% of the intensity at the center of the disk.
We can convert these formulas to functions of θ by using the substitution where Ω is the angle from the observer to the limb of the star. For small θ we have
We see that the derivative of cos ψ is infinite at the edge.
The above approximation can be used to derive an analytic expression for the ratio of the mean intensity to the central intensity. The mean intensity Im is the integral of the intensity over the disk of the star divided by the solid angle subtended by the disk:
where dω = sin θ dθ dφ is a solid angle element, and the integrals are over the disk: 0 ≤ φ ≤ 2π and 0 ≤ θ ≤ Ω. We may rewrite this as
Although this equation can be solved analytically, it is rather cumbersome. However, for an observer at infinite distance from the star, can be replaced by , so we have which gives
For the Sun at 550 nm, this says that the average intensity is 80.5% of the intensity at the center.
References
- Roun, Daniel (2003). "Limb Darkening". In Gargaud, Muriel; Amils, Ricardo; Quintanilla, José Cernicharo; Cleaves, Henderson James; Irvine, William M.; Pinti, Daniele L.; Viso, Michel (eds.). Encyclopedia of Astrobiology. Berlin, Heidelberg: Springer. pp. 925–926. doi:10.1007/978-3-642-11274-4_885. ISBN 978-3-642-11271-3.
- Cox, Arthur N., ed. (2000). Allen's Astrophysical Quantities (14th ed.). Springer-Verlag, NY. ISBN 0-387-98746-0.
- Billings, Donald E. (1966). A Guide to the Solar Corona. Academic Press, New York.
- Milne, E.A. (1921). "Radiative Equilibrium in the Outer Layers of a Star: the Temperature Distribution and the Law of Darkening". MNRAS. 81 (5): 361–375. Bibcode:1921MNRAS..81..361M. doi:10.1093/mnras/81.5.361 – via Zenodo.
- Minnaert, M. (1930). "On the Continuous Spectrum of the Corona and its Polarisation". Zeitschrift für Astrophysik. 1: 209. Bibcode:1930ZA......1..209M – via NASA/ADS.
- Neckel, H.; Labs, D. (1994). "Solar Limb Darkening 1986-1990". Solar Physics. 153 (1–2): 91–114. Bibcode:1994SoPh..153...91N. doi:10.1007/BF00712494. S2CID 119704650 – via NASA/ADS.
- van de Hulst; H. C. (1950). "The Electron Density of the Solar Corona". Bulletin of the Astronomical Institutes of the Netherlands. 11 (410): 135. Bibcode:1950BAN....11..135V.
- Mariska, John (1993). The Solar Transition Region. Cambridge University Press, Cambridge. ISBN 0521382610.
- Steiner, O. (2007). "Photospheric processes and magnetic flux tubes". AIP Conference Proceedings. 919: 74–121. arXiv:0709.0081. Bibcode:2007AIPC..919...74S. doi:10.1063/1.2756784. S2CID 16932214.
 where I(ψ) is the intensity seen at P along a line of sight forming angle ψ with respect to the stellar radius, and I(0) is the central intensity. In order that the ratio be unity for ψ = 0, we must have
where I(ψ) is the intensity seen at P along a line of sight forming angle ψ with respect to the stellar radius, and I(0) is the central intensity. In order that the ratio be unity for ψ = 0, we must have


 which now has N independent coefficients rather than N + 1 coefficients that must sum to unity.
which now has N independent coefficients rather than N + 1 coefficients that must sum to unity.


 where Ω is the angle from the observer to the limb of the star. For small θ we have
where Ω is the angle from the observer to the limb of the star. For small θ we have



 can be replaced by
can be replaced by  , so we have
, so we have
 which gives
which gives
