| Part of a series on | ||||
| Physical cosmology | ||||
|---|---|---|---|---|
 | ||||
Early universe
|
||||
| Expansion · Future | ||||
Components · Structure
|
||||
| Experiments | ||||
| Scientists | ||||
| Subject history | ||||
In physical cosmology, structure formation describes the creation of galaxies, galaxy clusters, and larger structures starting from small fluctuations in mass density resulting from processes that created matter. The universe, as is now known from observations of the cosmic microwave background radiation, began in a hot, dense, nearly uniform state approximately 13.8 billion years ago. However, looking at the night sky today, structures on all scales can be seen, from stars and planets to galaxies. On even larger scales, galaxy clusters and sheet-like structures of galaxies are separated by enormous voids containing few galaxies. Structure formation models gravitational instability of small ripples in mass density to predict these shapes, confirming the consistency of the physical model.
The modern Lambda-CDM model is successful at predicting the observed large-scale distribution of galaxies, clusters and voids; but on the scale of individual galaxies there are many complications due to highly nonlinear processes involving baryonic physics, gas heating and cooling, star formation and feedback. Understanding the processes of galaxy formation is a major topic of modern cosmology research, both via observations such as the Hubble Ultra-Deep Field and via large computer simulations.
Before the first structures
Structure formation began some time after recombination, when the early universe cooled enough from expansion to allow the formation of stable hydrogen and helium atoms. At this point the cosmic microwave background(CMB) is emitted; many careful measurements of the CMB provide key information about the initial state of the universe before structure formation. The measurements support a model of small fluctuations in density, critical seeds for structures to come.
Very early universe
In this stage, some mechanism, such as cosmic inflation, was responsible for establishing the initial conditions of the universe: homogeneity, isotropy, and flatness. Cosmic inflation also would have amplified minute quantum fluctuations (pre-inflation) into slight density ripples of overdensity and underdensity (post-inflation).
Growth of structure
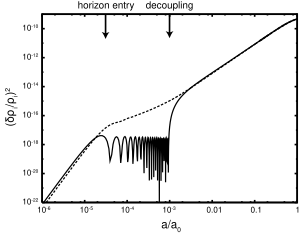
The early universe was dominated by radiation; in this case density fluctuations larger than the cosmic horizon grow proportional to the scale factor, as the gravitational potential fluctuations remain constant. Structures smaller than the horizon remained essentially frozen due to radiation domination impeding growth. As the universe expanded, the density of radiation drops faster than matter (due to redshifting of photon energy); this led to a crossover called matter-radiation equality at ~ 50,000 years after the Big Bang. After this all dark matter ripples could grow freely, forming seeds into which the baryons could later fall. The particle horizon at this epoch induces a turnover in the matter power spectrum which can be measured in large redshift surveys.
Recombination
The universe was dominated by radiation for most of this stage, and due to the intense heat and radiation, the primordial hydrogen and helium were fully ionized into nuclei and free electrons. In this hot and dense situation, the radiation (photons) could not travel far before Thomson scattering off an electron. The universe was very hot and dense, but expanding rapidly and therefore cooling. Finally, at a little less than 400,000 years after the 'bang', it became cool enough (around 3000 K) for the protons to capture negatively charged electrons, forming neutral hydrogen atoms. (Helium atoms formed somewhat earlier due to their larger binding energy). Once nearly all the charged particles were bound in neutral atoms, the photons no longer interacted with them and were free to propagate for the next 13.8 billion years; we currently detect those photons redshifted by a factor 1090 down to 2.725 K as the Cosmic Microwave Background Radiation (CMB) filling today's universe. Several remarkable space-based missions (COBE, WMAP, Planck), have detected very slight variations in the density and temperature of the CMB. These variations were subtle, and the CMB appears very nearly uniformly the same in every direction. However, the slight temperature variations of order a few parts in 100,000 are of enormous importance, for they essentially were early "seeds" from which all subsequent complex structures in the universe ultimately developed.
Dark matter structure
After the first matter condensed, the radiation traveled away, leaving a slightly inhomogeneous dark matter subject to gravitational interaction. The interaction eventually collapses the dark matter into "halos" that then attracts the normal or baryonic matter, primarily hydrogen. As the density of hydrogen increases due gravitational attraction, stars ignite, emitting ultraviolet light that re-ionizes any surrounding atoms. The gravitational interaction continues in hierarchical structure formation: the smaller gravitationally bound structures such as the first stars and stellar clusters form, then galaxies, followed by groups, clusters and superclusters of galaxies.
Linear structure
Dark matter plays a crucial role in structure formation because it feels only the force of gravity: the gravitational Jeans instability which allows compact structures to form is not opposed by any force, such as radiation pressure. As a result, dark matter begins to collapse into a complex network of dark matter halos well before ordinary matter, which is impeded by pressure forces. Without dark matter, the epoch of galaxy formation would occur substantially later in the universe than is observed.
The physics of structure formation in this epoch is particularly simple, as dark matter perturbations with different wavelengths evolve independently. As the Hubble radius grows in the expanding universe, it encompasses larger and larger disturbances. During matter domination, all causal dark matter perturbations grow through gravitational clustering. However, the shorter-wavelength perturbations that are included during radiation domination have their growth suppressed until matter domination. At this stage, luminous, baryonic matter is expected to mirror the evolution of the dark matter simply, and their distributions should closely trace one another.
It is straightforward to calculate this "linear power spectrum" and, as a tool for cosmology, it is of comparable importance to the cosmic microwave background. Galaxy surveys have measured the power spectrum, such as the Sloan Digital Sky Survey, and by surveys of the Lyman-α forest. Since these studies observe radiation emitted from galaxies and quasars, they do not directly measure the dark matter, but the large-scale distribution of galaxies (and of absorption lines in the Lyman-α forest) is expected to mirror the distribution of dark matter closely. This depends on the fact that galaxies will be larger and more numerous in denser parts of the universe, whereas they will be comparatively scarce in rarefied regions.
Nonlinear structure
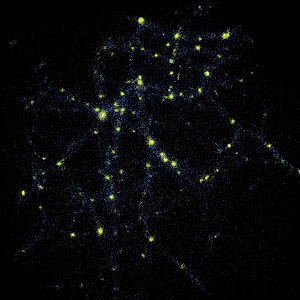
When the perturbations have grown sufficiently, a small region might become substantially denser than the mean density of the universe. At this point, the physics involved becomes substantially more complicated. When the deviations from homogeneity are small, the dark matter may be treated as a pressureless fluid and evolves by very simple equations. In regions which are significantly denser than the background, the full Newtonian theory of gravity must be included. (The Newtonian theory is appropriate because the masses involved are much less than those required to form a black hole, and the speed of gravity may be ignored as the light-crossing time for the structure is still smaller than the characteristic dynamical time.) One sign that the linear and fluid approximations become invalid is that dark matter starts to form caustics in which the trajectories of adjacent particles cross, or particles start to form orbits. These dynamics are best understood using N-body simulations (although a variety of semi-analytic schemes, such as the Press–Schechter formalism, can be used in some cases). While in principle these simulations are quite simple, in practice they are tough to implement, as they require simulating millions or even billions of particles. Moreover, despite the large number of particles, each particle typically weighs 10 solar masses and discretization effects may become significant. The largest such simulation as of 2005 is the Millennium simulation.
The result of N-body simulations suggests that the universe is composed largely of voids, whose densities might be as low as one-tenth the cosmological mean. The matter condenses in large filaments and haloes which have an intricate web-like structure. These form galaxy groups, clusters and superclusters. While the simulations appear to agree broadly with observations, their interpretation is complicated by the understanding of how dense accumulations of dark matter spur galaxy formation. In particular, many more small haloes form than we see in astronomical observations as dwarf galaxies and globular clusters. This is known as the Dwarf galaxy problem, and a variety of explanations have been proposed. Most account for it as an effect in the complicated physics of galaxy formation, but some have suggested that it is a problem with our model of dark matter and that some effect, such as warm dark matter, prevents the formation of the smallest haloes.
Gas evolution
See also: galaxy formation and evolution and stellar evolutionThe final stage in evolution comes when baryons condense in the centres of galaxy haloes to form galaxies, stars and quasars. Dark matter greatly accelerates the formation of dense haloes. As dark matter does not have radiation pressure, the formation of smaller structures from dark matter is impossible. This is because dark matter cannot dissipate angular momentum, whereas ordinary baryonic matter can collapse to form dense objects by dissipating angular momentum through radiative cooling. Understanding these processes is an enormously difficult computational problem, because they can involve the physics of gravity, magnetohydrodynamics, atomic physics, nuclear reactions, turbulence and even general relativity. In most cases, it is not yet possible to perform simulations that can be compared quantitatively with observations, and the best that can be achieved are approximate simulations that illustrate the main qualitative features of a process such as a star formation.
Modelling structure formation
Cosmological perturbations
Main article: cosmological perturbation theoryMuch of the difficulty, and many of the disputes, in understanding the large-scale structure of the universe can be resolved by better understanding the choice of gauge in general relativity. By the scalar-vector-tensor decomposition, the metric includes four scalar perturbations, two vector perturbations, and one tensor perturbation. Only the scalar perturbations are significant: the vectors are exponentially suppressed in the early universe, and the tensor mode makes only a small (but important) contribution in the form of primordial gravitational radiation and the B-modes of the cosmic microwave background polarization. Two of the four scalar modes may be removed by a physically meaningless coordinate transformation. Which modes are eliminated determine the infinite number of possible gauge fixings. The most popular gauge is Newtonian gauge (and the closely related conformal Newtonian gauge), in which the retained scalars are the Newtonian potentials Φ and Ψ, which correspond exactly to the Newtonian potential energy from Newtonian gravity. Many other gauges are used, including synchronous gauge, which can be an efficient gauge for numerical computation (it is used by CMBFAST). Each gauge still includes some unphysical degrees of freedom. There is a so-called gauge-invariant formalism, in which only gauge invariant combinations of variables are considered.
Inflation and initial conditions
The initial conditions for the universe are thought to arise from the scale invariant quantum mechanical fluctuations of cosmic inflation. The perturbation of the background energy density at a given point in space is then given by an isotropic, homogeneous Gaussian random field of mean zero. This means that the spatial Fourier transform of – has the following correlation functions
- ,
where is the three-dimensional Dirac delta function and is the length of . Moreover, the spectrum predicted by inflation is nearly scale invariant, which means
- ,
where is a small number. Finally, the initial conditions are adiabatic or isentropic, which means that the fractional perturbation in the entropy of each species of particle is equal. The resulting predictions fit very well with observations.
See also
- Big Bang – Physical theory
- Chronology of the universe – History and future of the universe
- Galaxy formation and evolution – Subfield of cosmology
- Illustris project – Computer-simulated universes
- Stellar evolution – Changes to stars over their lifespans
- Timeline of the Big Bang – History and future of the universePages displaying short descriptions of redirect targets
References
- "Cosmic Detectives". The European Space Agency (ESA). 2013-04-02. Retrieved 2013-04-15.
- Einasto, J.; Longair, M.S. (1978). "The Large Scale Structure of the Universe Symposium". Large Scale Structures in the Universe. 79. Reidel: 247. Bibcode:1978IAUS...79..241J.
- Dodelson, Scott (2003). Modern Cosmology. Academic Press. ISBN 978-0-12-219141-1.
- ^ Liddle, Andrew; David Lyth (2000). Cosmological Inflation and Large-Scale Structure. Cambridge. ISBN 978-0-521-57598-0.
- Padmanabhan, T. (1993). Structure formation in the universe. Cambridge University Press. ISBN 978-0-521-42486-8.
- Peebles, P. J. E. (1980). The Large-Scale Structure of the Universe. Princeton University Press. ISBN 978-0-691-08240-0.
- ^ Dayal, Pratika; Ferrara, Andrea (2018). "Early galaxy formation and its large-scale effects". Physics Reports. 780–782: 1–64. arXiv:1809.09136. Bibcode:2018PhR...780....1D. doi:10.1016/j.physrep.2018.10.002.
- Kolb, Edward; Michael Turner (1988). The Early Universe. Addison-Wesley. ISBN 978-0-201-11604-5.
- Springel, V.; et al. (2005). "Simulations of the formation, evolution and clustering of galaxies and quasars". Nature. 435 (7042): 629–636. arXiv:astro-ph/0504097. Bibcode:2005Natur.435..629S. doi:10.1038/nature03597. PMID 15931216. S2CID 4383030.
 in space is then given by an
in space is then given by an  –
–  has the following
has the following  ,
, is the three-dimensional
is the three-dimensional  is the length of
is the length of  . Moreover, the spectrum predicted by inflation is nearly
. Moreover, the spectrum predicted by inflation is nearly  ,
, is a small number. Finally, the initial conditions are adiabatic or isentropic, which means that the fractional perturbation in the entropy of each species of particle is equal.
The resulting predictions fit very well with observations.
is a small number. Finally, the initial conditions are adiabatic or isentropic, which means that the fractional perturbation in the entropy of each species of particle is equal.
The resulting predictions fit very well with observations.