Black-body radiation is the thermal electromagnetic radiation within, or surrounding, a body in thermodynamic equilibrium with its environment, emitted by a black body (an idealized opaque, non-reflective body). It has a specific, continuous spectrum of wavelengths, inversely related to intensity, that depend only on the body's temperature, which is assumed, for the sake of calculations and theory, to be uniform and constant.
A perfectly insulated enclosure which is in thermal equilibrium internally contains blackbody radiation, and will emit it through a hole made in its wall, provided the hole is small enough to have a negligible effect upon the equilibrium. The thermal radiation spontaneously emitted by many ordinary objects can be approximated as blackbody radiation.
Of particular importance, although planets and stars (including the Earth and Sun) are neither in thermal equilibrium with their surroundings nor perfect black bodies, blackbody radiation is still a good first approximation for the energy they emit.
The term black body was introduced by Gustav Kirchhoff in 1860. Blackbody radiation is also called thermal radiation, cavity radiation, complete radiation or temperature radiation.
Theory
Spectrum


Black-body radiation has a characteristic, continuous frequency spectrum that depends only on the body's temperature, called the Planck spectrum or Planck's law. The spectrum is peaked at a characteristic frequency that shifts to higher frequencies with increasing temperature, and at room temperature most of the emission is in the infrared region of the electromagnetic spectrum. As the temperature increases past about 500 degrees Celsius, black bodies start to emit significant amounts of visible light. Viewed in the dark by the human eye, the first faint glow appears as a "ghostly" grey (the visible light is actually red, but low intensity light activates only the eye's grey-level sensors). With rising temperature, the glow becomes visible even when there is some background surrounding light: first as a dull red, then yellow, and eventually a "dazzling bluish-white" as the temperature rises. When the body appears white, it is emitting a substantial fraction of its energy as ultraviolet radiation. The Sun, with an effective temperature of approximately 5800 K, is an approximate black body with an emission spectrum peaked in the central, yellow-green part of the visible spectrum, but with significant power in the ultraviolet as well.
Blackbody radiation provides insight into the thermodynamic equilibrium state of cavity radiation.
Black body
Main article: Black bodyAll normal (baryonic) matter emits electromagnetic radiation when it has a temperature above absolute zero. The radiation represents a conversion of a body's internal energy into electromagnetic energy, and is therefore called thermal radiation. It is a spontaneous process of radiative distribution of entropy.

Conversely, all normal matter absorbs electromagnetic radiation to some degree. An object that absorbs all radiation falling on it, at all wavelengths, is called a black body. When a black body is at a uniform temperature, its emission has a characteristic frequency distribution that depends on the temperature. Its emission is called blackbody radiation.
The concept of the black body is an idealization, as perfect black bodies do not exist in nature. However, graphite and lamp black, with emissivities greater than 0.95, are good approximations to a black material. Experimentally, blackbody radiation may be established best as the ultimately stable steady state equilibrium radiation in a cavity in a rigid body, at a uniform temperature, that is entirely opaque and is only partly reflective. A closed box with walls of graphite at a constant temperature with a small hole on one side produces a good approximation to ideal blackbody radiation emanating from the opening.
Blackbody radiation has the unique absolutely stable distribution of radiative intensity that can persist in thermodynamic equilibrium in a cavity. In equilibrium, for each frequency, the intensity of radiation which is emitted and reflected from a body relative to other frequencies (that is, the net amount of radiation leaving its surface, called the spectral radiance) is determined solely by the equilibrium temperature and does not depend upon the shape, material or structure of the body. For a black body (a perfect absorber) there is no reflected radiation, and so the spectral radiance is entirely due to emission. In addition, a black body is a diffuse emitter (its emission is independent of direction).
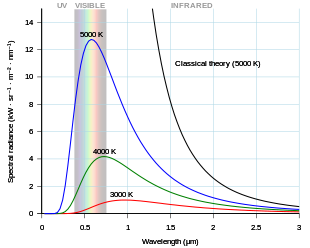
Blackbody radiation becomes a visible glow of light if the temperature of the object is high enough. The Draper point is the temperature at which all solids glow a dim red, about 798 K. At 1000 K, a small opening in the wall of a large uniformly heated opaque-walled cavity (such as an oven), viewed from outside, looks red; at 6000 K, it looks white. No matter how the oven is constructed, or of what material, as long as it is built so that almost all light entering is absorbed by its walls, it will contain a good approximation to blackbody radiation. The spectrum, and therefore color, of the light that comes out will be a function of the cavity temperature alone. A graph of the spectral radiation intensity plotted versus frequency(or wavelength) is called the blackbody curve. Different curves are obtained by varying the temperature.

When the body is black, the absorption is obvious: the amount of light absorbed is all the light that hits the surface. For a black body much bigger than the wavelength, the light energy absorbed at any wavelength λ per unit time is strictly proportional to the blackbody curve. This means that the blackbody curve is the amount of light energy emitted by a black body, which justifies the name. This is the condition for the applicability of Kirchhoff's law of thermal radiation: the blackbody curve is characteristic of thermal light, which depends only on the temperature of the walls of the cavity, provided that the walls of the cavity are completely opaque and are not very reflective, and that the cavity is in thermodynamic equilibrium. When the black body is small, so that its size is comparable to the wavelength of light, the absorption is modified, because a small object is not an efficient absorber of light of long wavelength, but the principle of strict equality of emission and absorption is always upheld in a condition of thermodynamic equilibrium.
In the laboratory, blackbody radiation is approximated by the radiation from a small hole in a large cavity, a hohlraum, in an entirely opaque body that is only partly reflective, that is maintained at a constant temperature. (This technique leads to the alternative term cavity radiation.) Any light entering the hole would have to reflect off the walls of the cavity multiple times before it escaped, in which process it is nearly certain to be absorbed. Absorption occurs regardless of the wavelength of the radiation entering (as long as it is small compared to the hole). The hole, then, is a close approximation of a theoretical black body and, if the cavity is heated, the spectrum of the hole's radiation (that is, the amount of light emitted from the hole at each wavelength) will be continuous, and will depend only on the temperature and the fact that the walls are opaque and at least partly absorptive, but not on the particular material of which they are built nor on the material in the cavity (compare with emission spectrum).
The radiance or observed intensity is not a function of direction. Therefore, a black body is a perfect Lambertian radiator.
Real objects never behave as full-ideal black bodies, and instead the emitted radiation at a given frequency is a fraction of what the ideal emission would be. The emissivity of a material specifies how well a real body radiates energy as compared with a black body. This emissivity depends on factors such as temperature, emission angle, and wavelength. However, it is typical in engineering to assume that a surface's spectral emissivity and absorptivity do not depend on wavelength so that the emissivity is a constant. This is known as the gray body assumption.

With non-black surfaces, the deviations from ideal blackbody behavior are determined by both the surface structure, such as roughness or granularity, and the chemical composition. On a "per wavelength" basis, real objects in states of local thermodynamic equilibrium still follow Kirchhoff's Law: emissivity equals absorptivity, so that an object that does not absorb all incident light will also emit less radiation than an ideal black body; the incomplete absorption can be due to some of the incident light being transmitted through the body or to some of it being reflected at the surface of the body.
In astronomy, objects such as stars are frequently regarded as black bodies, though this is often a poor approximation. An almost perfect blackbody spectrum is exhibited by the cosmic microwave background radiation. Hawking radiation is the hypothetical blackbody radiation emitted by black holes, at a temperature that depends on the mass, charge, and spin of the hole. If this prediction is correct, black holes will very gradually shrink and evaporate over time as they lose mass by the emission of photons and other particles.
A black body radiates energy at all frequencies, but its intensity rapidly tends to zero at high frequencies (short wavelengths). For example, a black body at room temperature (300 K) with one square meter of surface area will emit a photon in the visible range (390–750 nm) at an average rate of one photon every 41 seconds, meaning that, for most practical purposes, such a black body does not emit in the visible range.
The study of the laws of black bodies and the failure of classical physics to describe them helped establish the foundations of quantum mechanics.
Further explanation
According to the Classical Theory of Radiation, if each Fourier mode of the equilibrium radiation (in an otherwise empty cavity with perfectly reflective walls) is considered as a degree of freedom capable of exchanging energy, then, according to the equipartition theorem of classical physics, there would be an equal amount of energy in each mode. Since there are an infinite number of modes, this would imply infinite heat capacity, as well as a nonphysical spectrum of emitted radiation that grows without bound with increasing frequency, a problem known as the ultraviolet catastrophe. In the longer wavelengths this deviation is not so noticeable, as and are very small. In the shorter wavelengths of the ultraviolet range, however, classical theory predicts the energy emitted tends to infinity, hence the ultraviolet catastrophe. The theory even predicted that all bodies would emit most of their energy in the ultraviolet range, clearly contradicted by the experimental data which showed a different peak wavelength at different temperatures (see also Wien's law).
Instead, in the quantum treatment of this problem, the numbers of the energy modes are quantized, attenuating the spectrum at high frequency in agreement with experimental observation and resolving the catastrophe. The modes that had more energy than the thermal energy of the substance itself were not considered, and because of quantization modes having infinitesimally little energy were excluded.
Thus for shorter wavelengths very few modes (having energy more than ) were allowed, supporting the data that the energy emitted is reduced for wavelengths less than the wavelength of the observed peak of emission.
Notice that there are two factors responsible for the shape of the graph, which can be seen as working opposite to one another. Firstly, shorter wavelengths have a larger number of modes associated with them. This accounts for the increase in spectral radiance as one moves from the longest wavelengths towards the peak at relatively shorter wavelengths. Secondly, though, at shorter wavelengths more energy is needed to reach the threshold level to occupy each mode: the more energy needed to excite the mode, the lower the probability that this mode will be occupied. As the wavelength decreases, the probability of exciting the mode becomes exceedingly small, leading to fewer of these modes being occupied: this accounts for the decrease in spectral radiance at very short wavelengths, left of the peak. Combined, they give the characteristic graph.
Calculating the blackbody curve was a major challenge in theoretical physics during the late nineteenth century. The problem was solved in 1901 by Max Planck in the formalism now known as Planck's law of blackbody radiation. By making changes to Wien's radiation law (not to be confused with Wien's displacement law) consistent with thermodynamics and electromagnetism, he found a mathematical expression fitting the experimental data satisfactorily. Planck had to assume that the energy of the oscillators in the cavity was quantized, which is to say that it existed in integer multiples of some quantity. Einstein built on this idea and proposed the quantization of electromagnetic radiation itself in 1905 to explain the photoelectric effect. These theoretical advances eventually resulted in the superseding of classical electromagnetism by quantum electrodynamics. These quanta were called photons and the blackbody cavity was thought of as containing a gas of photons. In addition, it led to the development of quantum probability distributions, called Fermi–Dirac statistics and Bose–Einstein statistics, each applicable to a different class of particles, fermions and bosons.
The wavelength at which the radiation is strongest is given by Wien's displacement law, and the overall power emitted per unit area is given by the Stefan–Boltzmann law. So, as temperature increases, the glow color changes from red to yellow to white to blue. Even as the peak wavelength moves into the ultra-violet, enough radiation continues to be emitted in the blue wavelengths that the body will continue to appear blue. It will never become invisible—indeed, the radiation of visible light increases monotonically with temperature. The Stefan–Boltzmann law also says that the total radiant heat energy emitted from a surface is proportional to the fourth power of its absolute temperature. The law was formulated by Josef Stefan in 1879 and later derived by Ludwig Boltzmann. The formula E = σT is given, where E is the radiant heat emitted from a unit of area per unit time, T is the absolute temperature, and σ = 5.670367×10 W·m⋅K is the Stefan–Boltzmann constant.
Equations
Planck's law of blackbody radiation
Main article: Planck's lawPlanck's law states that where
- is the spectral radiance (the power per unit solid angle and per unit of area normal to the propagation) density of frequency radiation per unit frequency at thermal equilibrium at temperature . Units: power / .
- is the Planck constant;
- is the speed of light in vacuum;
- is the Boltzmann constant;
- is the frequency of the electromagnetic radiation;
- is the absolute temperature of the body.
For a black body surface, the spectral radiance density (defined per unit of area normal to the propagation) is independent of the angle of emission with respect to the normal. However, this means that, following Lambert's cosine law, is the radiance density per unit area of emitting surface as the surface area involved in generating the radiance is increased by a factor with respect to an area normal to the propagation direction. At oblique angles, the solid angle spans involved do get smaller, resulting in lower aggregate intensities.
The emitted energy flux density or irradiance , is related to the photon flux density through
Wien's displacement law
Main article: Wien's displacement lawWien's displacement law shows how the spectrum of blackbody radiation at any temperature is related to the spectrum at any other temperature. If we know the shape of the spectrum at one temperature, we can calculate the shape at any other temperature. Spectral intensity can be expressed as a function of wavelength or of frequency.
A consequence of Wien's displacement law is that the wavelength at which the intensity per unit wavelength of the radiation produced by a black body has a local maximum or peak, , is a function only of the temperature: where the constant b, known as Wien's displacement constant, is equal to 2.897771955×10 m K. is the Lambert W function. So is approximately 2898 μm/T, with the temperature given in kelvins. At a typical room temperature of 293 K (20 °C), the maximum intensity is at 9.9 μm.
Planck's law was also stated above as a function of frequency. The intensity maximum for this is given by In unitless form, the maximum occurs when , where . The approximate numerical solution is . At a typical room temperature of 293 K (20 °C), the maximum intensity is for = 17 THz.
Stefan–Boltzmann law
By integrating over the frequency the radiance (units: power / ) is by using with and with being the Stefan–Boltzmann constant.
On a side note, at a distance d, the intensity per area of radiating surface is the useful expression when the receiving surface is perpendicular to the radiation.
By subsequently integrating over the solid angle for all azimuthal angle (0 to ) and polar angle from 0 to , we arrive at the Stefan–Boltzmann law: the power j* emitted per unit area of the surface of a black body is directly proportional to the fourth power of its absolute temperature: We used
Applications
Human-body emission

 Much of a person's energy is radiated away in the form of long-wave infrared (LWIR) light. Some materials are transparent in the infrared, but opaque to visible light, as is the plastic bag in this thermal (LWIR) camera image (bottom). Other materials are transparent to visible light, but opaque or reflective in the infrared, noticeable by the darkness of the man's glasses.
Much of a person's energy is radiated away in the form of long-wave infrared (LWIR) light. Some materials are transparent in the infrared, but opaque to visible light, as is the plastic bag in this thermal (LWIR) camera image (bottom). Other materials are transparent to visible light, but opaque or reflective in the infrared, noticeable by the darkness of the man's glasses.
The human body radiates energy as infrared light. The net power radiated is the difference between the power emitted and the power absorbed: Applying the Stefan–Boltzmann law, where A and T are the body surface area and temperature, is the emissivity, and T0 is the ambient temperature.
The total surface area of an adult is about 2 m, and the mid- and far-infrared emissivity of skin and most clothing is near unity, as it is for most nonmetallic surfaces. Skin temperature is about 33 °C, but clothing reduces the surface temperature to about 28 °C when the ambient temperature is 20 °C. Hence, the net radiative heat loss is about The total energy radiated in one day is about 8 MJ, or 2000 kcal (food calories). Basal metabolic rate for a 40-year-old male is about 35 kcal/(m·h), which is equivalent to 1700 kcal per day, assuming the same 2 m area. However, the mean metabolic rate of sedentary adults is about 50% to 70% greater than their basal rate.
There are other important thermal loss mechanisms, including convection and evaporation. Conduction is negligible – the Nusselt number is much greater than unity. Evaporation by perspiration is only required if radiation and convection are insufficient to maintain a steady-state temperature (but evaporation from the lungs occurs regardless). Free-convection rates are comparable, albeit somewhat lower, than radiative rates. Thus, radiation accounts for about two-thirds of thermal energy loss in cool, still air. Given the approximate nature of many of the assumptions, this can only be taken as a crude estimate. Ambient air motion, causing forced convection, or evaporation reduces the relative importance of radiation as a thermal-loss mechanism.
Application of Wien's law to human-body emission results in a peak wavelength of For this reason, thermal imaging devices for human subjects are most sensitive in the 7–14 micrometer range.
Temperature relation between a planet and its star
Main article: Planetary equilibrium temperatureThe blackbody law may be used to estimate the temperature of a planet orbiting the Sun.

The temperature of a planet depends on several factors:
- Incident radiation from its star
- Emitted radiation of the planet (for example, Earth's infrared glow)
- The albedo effect causing a fraction of light to be reflected by the planet
- The greenhouse effect for planets with an atmosphere
- Energy generated internally by a planet itself due to radioactive decay, tidal heating, and adiabatic contraction due to cooling.
The analysis only considers the Sun's heat for a planet in a Solar System.
The Stefan–Boltzmann law gives the total power (energy/second) that the Sun emits:

| 1 |
where
- is the Stefan–Boltzmann constant,
- is the effective temperature of the Sun, and
- is the radius of the Sun.
The Sun emits that power equally in all directions. Because of this, the planet is hit with only a tiny fraction of it. The power from the Sun that strikes the planet (at the top of the atmosphere) is:
| 2 |
where
- is the radius of the planet, and
- is the distance between the Sun and the planet.
Because of its high temperature, the Sun emits to a large extent in the ultraviolet and visible (UV-Vis) frequency range. In this frequency range, the planet reflects a fraction of this energy where is the albedo or reflectance of the planet in the UV-Vis range. In other words, the planet absorbs a fraction of the Sun's light, and reflects the rest. The power absorbed by the planet and its atmosphere is then:
| 3 |
Even though the planet only absorbs as a circular area , it emits in all directions; the spherical surface area being . If the planet were a perfect black body, it would emit according to the Stefan–Boltzmann law
| 4 |
where is the temperature of the planet. This temperature, calculated for the case of the planet acting as a black body by setting , is known as the effective temperature. The actual temperature of the planet will likely be different, depending on its surface and atmospheric properties. Ignoring the atmosphere and greenhouse effect, the planet, since it is at a much lower temperature than the Sun, emits mostly in the infrared (IR) portion of the spectrum. In this frequency range, it emits of the radiation that a black body would emit where is the average emissivity in the IR range. The power emitted by the planet is then:
| 5 |
For a body in radiative exchange equilibrium with its surroundings, the rate at which it emits radiant energy is equal to the rate at which it absorbs it:
| 6 |
Substituting the expressions for solar and planet power in equations 1–6 and simplifying yields the estimated temperature of the planet, ignoring greenhouse effect, TP:
| 7 |
In other words, given the assumptions made, the temperature of a planet depends only on the surface temperature of the Sun, the radius of the Sun, the distance between the planet and the Sun, the albedo and the IR emissivity of the planet.
Notice that a gray (flat spectrum) ball where comes to the same temperature as a black body no matter how dark or light gray.
Effective temperature of Earth
Substituting the measured values for the Sun and Earth yields:
With the average emissivity set to unity, the effective temperature of the Earth is: or −18.8 °C.
This is the temperature of the Earth if it radiated as a perfect black body in the infrared, assuming an unchanging albedo and ignoring greenhouse effects (which can raise the surface temperature of a body above what it would be if it were a perfect black body in all spectrums). The Earth in fact radiates not quite as a perfect black body in the infrared which will raise the estimated temperature a few degrees above the effective temperature. If we wish to estimate what the temperature of the Earth would be if it had no atmosphere, then we could take the albedo and emissivity of the Moon as a good estimate. The albedo and emissivity of the Moon are about 0.1054 and 0.95 respectively, yielding an estimated temperature of about 1.36 °C.
Estimates of the Earth's average albedo vary in the range 0.3–0.4, resulting in different estimated effective temperatures. Estimates are often based on the solar constant (total insolation power density) rather than the temperature, size, and distance of the Sun. For example, using 0.4 for albedo, and an insolation of 1400 W m, one obtains an effective temperature of about 245 K. Similarly using albedo 0.3 and solar constant of 1372 W m, one obtains an effective temperature of 255 K.
Cosmology
The cosmic microwave background radiation observed today is the most perfect blackbody radiation ever observed in nature, with a temperature of about 2.7 K. It is a "snapshot" of the radiation at the time of decoupling between matter and radiation in the early universe. Prior to this time, most matter in the universe was in the form of an ionized plasma in thermal, though not full thermodynamic, equilibrium with radiation.
According to Kondepudi and Prigogine, at very high temperatures (above 10 K; such temperatures existed in the very early universe), where the thermal motion separates protons and neutrons in spite of the strong nuclear forces, electron-positron pairs appear and disappear spontaneously and are in thermal equilibrium with electromagnetic radiation. These particles form a part of the black body spectrum, in addition to the electromagnetic radiation.
A black body at room temperature (23 °C (296 K; 73 °F)) radiates mostly in the infrared spectrum, which cannot be perceived by the human eye, but can be sensed by some reptiles. As the object increases in temperature to about 500 °C (773 K; 932 °F), the emission spectrum gets stronger and extends into the human visual range, and the object appears dull red. As its temperature increases further, it emits more and more orange, yellow, green, and then blue light (and ultimately beyond violet, ultraviolet).
Light bulb
Tungsten filament lights have a continuous black body spectrum with a cooler colour temperature, around 2,700 K (2,430 °C; 4,400 °F), which also emits considerable energy in the infrared range. Modern-day fluorescent and LED lights, which are more efficient, do not have a continuous black body emission spectrum, rather emitting directly, or using combinations of phosphors that emit multiple narrow spectrums.

History
In query 6 of Isaac Newton's Opticks, he states that "Do not black Bodies conceive heat more easily from Light than those of other Colours do, by reason that the Light falling on them is not reflected outwards, but enters into the Bodies, and is often reflected and refracted within them, until it be stifled and lost?", thereby introducing the notion of a black body. In his first memoir, Augustin-Jean Fresnel (1788–1827) responded to a view he extracted from a French translation of Newton's Opticks. He says that Newton imagined particles of light traversing space uninhibited by the caloric medium filling it, and refutes this view (never actually held by Newton) by saying that a black body under illumination would increase indefinitely in heat.
Balfour Stewart
In 1858, Balfour Stewart described his experiments on the thermal radiative emissive and absorptive powers of polished plates of various substances, compared with the powers of lamp-black surfaces, at the same temperature. Stewart chose lamp-black surfaces as his reference because of various previous experimental findings, especially those of Pierre Prevost and of John Leslie. He wrote, "Lamp-black, which absorbs all the rays that fall upon it, and therefore possesses the greatest possible absorbing power, will possess also the greatest possible radiating power." Stewart's statement assumed a general principle: that there exists a body or surface that has the greatest possible absorbing and radiative power for every wavelength and equilibrium temperature.
Stewart was concerned with selective thermal radiation, which he investigated using plates which selectively radiated and absorbed different wavelengths. He discussed the experiments in terms of rays which could be reflected and refracted, and which obeyed the Stokes-Helmholtz reciprocity principle. His research did not consider that properties of rays are dependent on wavelength, and he did not use tools such as prisms or diffraction gratings. His work was quantitative within these constraints. He made his measurements in a room temperature environment, and quickly so as to catch his bodies in a condition near the thermal equilibrium in which they had been prepared.
Gustav Kirchhoff
In 1859, Gustav Robert Kirchhoff reported the coincidence of the wavelengths of spectrally resolved lines of absorption and emission of visible light. Importantly for thermal physics, he also observed that bright lines or dark lines were apparent depending on the temperature difference between emitter and absorber.
Kirchhoff then went on to consider some bodies that emit and absorb heat radiation, in an opaque enclosure or cavity, in equilibrium at a temperature T.
Here is used a notation different from Kirchhoff's. Here, the emitting power E(T, i) denotes a dimensioned quantity, the total radiation emitted by a body labeled by index i at temperature T. The total absorption ratio a(T, i) of that body is dimensionless, the ratio of absorbed to incident radiation in the cavity at temperature T . (In contrast with Balfour Stewart's, Kirchhoff's definition of his absorption ratio did not refer in particular to a lamp-black surface as the source of the incident radiation.) Thus the ratio E(T, i) / a(T, i) of emitting power to absorptivity is a dimensioned quantity, with the dimensions of emitting power, because a(T, i) is dimensionless. Also here the wavelength-specific emitting power of the body at temperature T is denoted by E(λ, T, i) and the wavelength-specific absorption ratio by a(λ, T, i) . Again, the ratio E(λ, T, i) / a(λ, T, i) of emitting power to absorptivity is a dimensioned quantity, with the dimensions of emitting power.
In a second report made in 1859, Kirchhoff announced a new general principle or law for which he offered a theoretical and mathematical proof, though he did not offer quantitative measurements of radiation powers. His theoretical proof was and still is considered by some writers to be invalid. His principle, however, has endured: it was that for heat rays of the same wavelength, in equilibrium at a given temperature, the wavelength-specific ratio of emitting power to absorptivity has one and the same common value for all bodies that emit and absorb at that wavelength. In symbols, the law stated that the wavelength-specific ratio E(λ, T, i) / a(λ, T, i) has one and the same value for all bodies. In this report there was no mention of black bodies.
In 1860, still not knowing of Stewart's measurements for selected qualities of radiation, Kirchhoff pointed out that it was long established experimentally that for total heat radiation emitted and absorbed by a body in equilibrium, the dimensioned total radiation ratio E(T, i) / a(T, i) has one and the same value common to all bodies. Again without measurements of radiative powers or other new experimental data, Kirchhoff then offered a fresh theoretical proof of his new principle of the universality of the value of the wavelength-specific ratio E(λ, T, i) / a(λ, T, i) at thermal equilibrium. His fresh theoretical proof was and still is considered by some writers to be invalid.
But more importantly, it relied on a new theoretical postulate of "perfectly black bodies," which is the reason why one speaks of Kirchhoff's law. Such black bodies showed complete absorption in their infinitely thin most superficial surface. They correspond to Balfour Stewart's reference bodies, with internal radiation, coated with lamp-black. They were not the more realistic perfectly black bodies later considered by Planck. Planck's black bodies radiated and absorbed only by the material in their interiors; their interfaces with contiguous media were only mathematical surfaces, capable neither of absorption nor emission, but only of reflecting and transmitting with refraction.
Kirchhoff's proof considered an arbitrary non-ideal body labeled i as well as various perfect black bodies labeled BB. It required that the bodies be kept in a cavity in thermal equilibrium at temperature T. His proof intended to show that the ratio E(λ, T, i) / a(λ, T, i) was independent of the nature i of the non-ideal body, however partly transparent or partly reflective it was.
His proof first argued that for wavelength λ and at temperature T, at thermal equilibrium, all perfectly black bodies of the same size and shape have the one and the same common value of emissive power E(λ, T, BB), with the dimensions of power. His proof noted that the dimensionless wavelength-specific absorptivity a(λ, T, BB) of a perfectly black body is by definition exactly 1. Then for a perfectly black body, the wavelength-specific ratio of emissive power to absorptivity E(λ, T, BB) / a(λ, T, BB) is again just E(λ, T, BB), with the dimensions of power. Kirchhoff considered thermal equilibrium with the arbitrary non-ideal body, and with a perfectly black body of the same size and shape, in place in his cavity in equilibrium at temperature T. He argued that the flows of heat radiation must be the same in each case. Thus he argued that at thermal equilibrium the ratio E(λ, T, i) / a(λ, T, i) was equal to E(λ, T, BB), which may now be denoted Bλ (λ, T). Bλ (λ, T) is a continuous function, dependent only on λ at fixed temperature T, and an increasing function of T at fixed wavelength λ. It vanishes at low temperatures for visible wavelengths, which does not depend on the nature i of the arbitrary non-ideal body (Geometrical factors, taken into detailed account by Kirchhoff, have been ignored in the foregoing).
Thus Kirchhoff's law of thermal radiation can be stated: For any material at all, radiating and absorbing in thermodynamic equilibrium at any given temperature T, for every wavelength λ, the ratio of emissive power to absorptivity has one universal value, which is characteristic of a perfect black body, and is an emissive power which we here represent by Bλ (λ, T). (For our notation Bλ (λ, T), Kirchhoff's original notation was simply e.)
Kirchhoff announced that the determination of the function Bλ (λ, T) was a problem of the highest importance, though he recognized that there would be experimental difficulties to be overcome. He supposed that like other functions that do not depend on the properties of individual bodies, it would be a simple function. Occasionally by historians that function Bλ (λ, T) has been called "Kirchhoff's (emission, universal) function," though its precise mathematical form would not be known for another forty years, till it was discovered by Planck in 1900. The theoretical proof for Kirchhoff's universality principle was worked on and debated by various physicists over the same time, and later. Kirchhoff stated later in 1860 that his theoretical proof was better than Balfour Stewart's, and in some respects it was so. Kirchhoff's 1860 paper did not mention the second law of thermodynamics, and of course did not mention the concept of entropy which had not at that time been established. In a more considered account in a book in 1862, Kirchhoff mentioned the connection of his law with Carnot's principle, which is a form of the second law.
According to Helge Kragh, "Quantum theory owes its origin to the study of thermal radiation, in particular to the "blackbody" radiation that Robert Kirchhoff had first defined in 1859–1860."
Doppler effect
The relativistic Doppler effect causes a shift in the frequency f of light originating from a source that is moving in relation to the observer, so that the wave is observed to have frequency f': where v is the velocity of the source in the observer's rest frame, θ is the angle between the velocity vector and the observer-source direction measured in the reference frame of the source, and c is the speed of light. This can be simplified for the special cases of objects moving directly towards (θ = π) or away (θ = 0) from the observer, and for speeds much less than c.
Through Planck's law the temperature spectrum of a black body is proportionally related to the frequency of light and one may substitute the temperature (T) for the frequency in this equation.
For the case of a source moving directly towards or away from the observer, this reduces to Here v > 0 indicates a receding source, and v < 0 indicates an approaching source.
This is an important effect in astronomy, where the velocities of stars and galaxies can reach significant fractions of c. An example is found in the cosmic microwave background radiation, which exhibits a dipole anisotropy from the Earth's motion relative to this blackbody radiation field.
See also
- Bolometer
- Color temperature
- Draper point
- Infrared thermometer
- Photon polarization
- Planck's law
- Pyrometer
- Rayleigh–Jeans law
- Sakuma–Hattori equation
- Terahertz radiation
- Thermography
- Wien approximation
References
- Loudon 2000, Chapter 1.
- Mandel & Wolf 1995, Chapter 13.
- Kondepudi & Prigogine 1998, Chapter 11.
- Landsberg 1990, Chapter 13.
- Ian Morison (2008). Introduction to Astronomy and Cosmology. J Wiley & Sons. p. 48. ISBN 978-0-470-03333-3.
- From (Kirchhoff, 1860) (Annalen der Physik und Chemie), p. 277: "Der Beweis, welcher für die ausgesprochene Behauptung hier gegeben werden soll, … vollkommen schwarze, oder kürzer schwarze, nennen." (The proof, which shall be given here for the proposition stated , rests on the assumption that bodies are conceivable which in the case of infinitely small thicknesses, completely absorb all rays that fall on them, thus neither reflect nor transmit rays. I will call such bodies "completely black " or more briefly "black ".) See also (Kirchhoff, 1860) (Philosophical Magazine), p. 2.
- Dustin (18 December 2018). "How Do Blacksmiths Measure The Temperature Of Their Forge And Steel?". Blacksmith U.
- Tomokazu Kogure; Kam-Ching Leung (2007). "§2.3: Thermodynamic equilibrium and blackbody radiation". The astrophysics of emission-line stars. Springer. p. 41. ISBN 978-0-387-34500-0.
- Wien, W. (1893). Eine neue Beziehung der Strahlung schwarzer Körper zum zweiten Hauptsatz der Wärmetheorie, Sitzungberichte der Königlich-Preußischen Akademie der Wissenschaften (Berlin), 1893, 1: 55–62.
- Lummer, O., Pringsheim, E. (1899). Die Vertheilung der Energie im Spectrum des schwarzen Körpers, Verhandlungen der Deutschen Physikalischen Gessellschaft (Leipzig), 1899, 1: 23–41.
- Planck 1914
- Draper, J.W. (1847). On the production of light by heat, London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, series 3, 30: 345–360.
- Partington 1949, pp. 466–467, 478
- Goody & Yung 1989, pp. 482, 484
- ^ Planck 1914, p. 42
- Wien 1894
- Planck 1914, p. 43
- Joseph Caniou (1999). "§4.2.2: Calculation of Planck's law". Passive infrared detection: theory and applications. Springer. p. 107. ISBN 0-7923-8532-2.
- Mekhrengin, M.V.; Meshkovskii, I.K.; Tashkinov, V.A.; Guryev, V.I.; Sukhinets, A.V.; Smirnov, D.S. (June 2019). "Multispectral pyrometer for high temperature measurements inside combustion chamber of gas turbine engines". Measurement. 139: 355–360. Bibcode:2019Meas..139..355M. doi:10.1016/j.measurement.2019.02.084. S2CID 116260472.
- J. R. Mahan (2002). Radiation heat transfer: a statistical approach (3rd ed.). Wiley-IEEE. p. 58. ISBN 978-0-471-21270-6.
- Huang, Kerson (1967). Statistical Mechanics. New York: John Wiley & Sons. ISBN 0-471-81518-7.
- Gannon, Megan (December 21, 2012). "New 'Baby Picture' of Universe Unveiled". Space.com. Retrieved December 21, 2012.
- Bennett, C.L.; Larson, L.; Weiland, J.L.; Jarosk, N.; Hinshaw, N.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; Komatsu, E.; Nolta, M.R.; Page, L.; Spergel, D.N.; Wollack, E.; Dunkley, J.; Kogut, A.; Limon, M.; Meyer, S.S.; Tucker, G.S.; Wright, E.L. (December 20, 2012). "Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results". The Astrophysical Journal Supplement Series. 1212 (2): 5225. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.
- Ling, Samuel J.; Sanny, Jeff; Moebs, William (2021). "6.2 Blackbody Radiation". University Physics Volume 3. Rice University. Retrieved 2024-11-12.
- "Blackbody Radiation".
- Planck, Max (1901). "Ueber das Gesetz der Energieverteilung im Normalspectrum" [On the law of the distribution of energy in the normal spectrum]. Annalen der Physik. 4th series (in German). 4 (3): 553–563. Bibcode:1901AnP...309..553P. doi:10.1002/andp.19013090310.
- Landau, L. D.; E. M. Lifshitz (1996). Statistical Physics (3rd Edition Part 1 ed.). Oxford: Butterworth–Heinemann. ISBN 0-521-65314-2.
- "Stefan-Boltzmann law". Encyclopædia Britannica. 2019.
- Rybicki & Lightman 1979, p. 22
- Jenny Nelson (2002). The Physics of Solar Cells. Imperial College Press. p. 19. doi:10.1142/p276. ISBN 978-1-86094-340-9.
- "Wien wavelength displacement law constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. Retrieved July 8, 2023.
- Nave, Dr. Rod. "Wien's Displacement Law and Other Ways to Characterize the Peak of Blackbody Radiation". HyperPhysics. Provides 5 variations of Wien's displacement law
- Infrared Services. "Emissivity Values for Common Materials". Archived from the original on 2007-06-25. Retrieved 2007-06-24.
- Omega Engineering. "Emissivity of Common Materials". Retrieved 2007-06-24.
- Farzana, Abanty (2001). "Temperature of a Healthy Human (Skin Temperature)". The Physics Factbook. Retrieved 2007-06-24.
- Lee, B. "Theoretical Prediction and Measurement of the Fabric Surface Apparent Temperature in a Simulated Man/Fabric/Environment System" (PDF). Archived from the original (PDF) on 2006-09-02. Retrieved 2007-06-24.
- Harris J, Benedict F; Benedict (1918). "A Biometric Study of Human Basal Metabolism". Proc Natl Acad Sci USA. 4 (12): 370–3. Bibcode:1918PNAS....4..370H. doi:10.1073/pnas.4.12.370. PMC 1091498. PMID 16576330.
- Levine, J (2004). "Nonexercise activity thermogenesis (NEAT): environment and biology". Am J Physiol Endocrinol Metab. 286 (5): E675 – E685. doi:10.1152/ajpendo.00562.2003. PMID 15102614.
- DrPhysics.com. "Heat Transfer and the Human Body". Retrieved 2007-06-24.
- Prevost, P. (1791). "Mémoire sur l'équilibre du feu". Journal de Physique (Paris). 38: 314–322.
- Iribarne, J.V., Godson, W.L. (1981). Atmospheric Thermodynamics, second edition, D. Reidel Publishing, Dordrecht, ISBN 90-277-1296-4, page 227.
- ^ NASA Sun Fact Sheet
- Cole, George H. A.; Woolfson, Michael M. (2002). Planetary Science: The Science of Planets Around Stars (1st ed.). IOP Publishing. pp. 36–37, 380–382. ISBN 0-7503-0815-X.
- Principles of Planetary Climate by Raymond T. Peirrehumbert, Cambridge University Press (2011), p. 146. From Chapter 3 which is available online here Archived March 28, 2012, at the Wayback Machine, p. 12 mentions that Venus' blackbody temperature would be 330 K "in the zero albedo case", but that due to atmospheric warming, its actual surface temperature is 740 K.
- Saari, J. M.; Shorthill, R. W. (1972). "The Sunlit Lunar Surface. I. Albedo Studies and Full Moon". The Moon. 5 (1–2): 161–178. Bibcode:1972Moon....5..161S. doi:10.1007/BF00562111. S2CID 119892155.
- Lunar and Planetary Science XXXVII (2006) 2406
- Michael D. Papagiannis (1972). Space physics and space astronomy. Taylor & Francis. pp. 10–11. ISBN 978-0-677-04000-4.
- Willem Jozef Meine Martens & Jan Rotmans (1999). Climate Change an Integrated Perspective. Springer. pp. 52–55. ISBN 978-0-7923-5996-8.
- F. Selsis (2004). "The Prebiotic Atmosphere of the Earth". In Pascale Ehrenfreund; et al. (eds.). Astrobiology: Future Perspectives. Springer. pp. 279–280. ISBN 978-1-4020-2587-7.
- Wallace, J.M., Hobbs, P.V. (2006). Atmospheric Science. An Introductory Survey, second edition, Elsevier, Amsterdam, ISBN 978-0-12-732951-2, exercise 4.6, pages 119–120.
- White, M. (1999). "Anisotropies in the CMB". arXiv:astro-ph/9903232. Bibcode:1999dpf..conf.....W.
- Kondepudi & Prigogine 1998, pp. 227–228; also Section 11.6, pages 294–296.
- Partington, J.R. (1949), p. 466.
- Bochner, Salomon (1981). Role of Mathematics in the Rise of Science (1. Princeton paperback pr ed.). Princeton, NJ: Princeton Univ. Pr. p. 347. ISBN 978-0-691-08028-4.
- Gunning, Robert C., ed. (1992). Collected Papers of Salomon Bochner. Vol. IV. Providence, R.I: American Mathematical Society. p. 133. ISBN 978-0-8218-0161-1.
- Rowlands, Peter (2017). Newton - Innovation And Controversy. World Scientific Publishing. p. 69. ISBN 9781786344045.
- Gillispie, Charles Coulston (1960). The Edge of Objectivity: An Essay in the History of Scientific Ideas. Princeton University Press. pp. 408–9. ISBN 0-691-02350-6.
- Stewart 1858
- Kirchhoff 1860a
- Kirchhoff 1860b
- ^ Siegel 1976
- ^ Schirrmacher 2001
- ^ Kirchhoff 1860c
- Planck 1914, p. 11
- Chandrasekhar 1950, p. 8
- Milne 1930, p. 80
- Rybicki & Lightman 1979, pp. 16–17
- Mihalas & Weibel-Mihalas 1984, p. 328
- Goody & Yung 1989, pp. 27–28
- Paschen, F. (1896), personal letter cited by Hermann 1971, p. 6
- Hermann 1971, p. 7
- Kuhn 1978, pp. 8, 29
- Mehra & Rechenberg 1982, pp. 26, 28, 31, 39
- Kirchhoff & 1862/1882, p. 573
- Kragh 1999, p. 58
- The Doppler Effect, T. P. Gill, Logos Press, 1965
Bibliography
- Chandrasekhar, S. (1950). Radiative Transfer. Oxford University Press.
- Goody, R. M.; Yung, Y. L. (1989). Atmospheric Radiation: Theoretical Basis (2nd ed.). Oxford University Press. ISBN 978-0-19-510291-8.
- Hermann, A. (1971). The Genesis of Quantum Theory. Nash, C.W. (transl.). MIT Press. ISBN 0-262-08047-8. a translation of Frühgeschichte der Quantentheorie (1899–1913), Physik Verlag, Mosbach/Baden.
- Kirchhoff, G.; (1860a). "Über die Fraunhofer'schen Linien" [On Fraunhofer's lines]. Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin: 662–665.
{{cite journal}}: CS1 maint: numeric names: authors list (link) - Kirchhoff, G.; (1860b). "Über den Zusammenhang zwischen Emission und Absorption von Licht und Wärme" [On the relation between emission and absorption of light and heat]. Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin: 783–787.
{{cite journal}}: CS1 maint: numeric names: authors list (link) - Kirchhoff, G. (1860c). "Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme and Licht" [On the relation between bodies' emission capacity and absorption capacity for heat and light]. Annalen der Physik und Chemie. 109 (2): 275–301. Bibcode:1860AnP...185..275K. doi:10.1002/andp.18601850205. Translated by Guthrie, F. as Kirchhoff, G. (1860). "On the relation between the radiating and absorbing powers of different bodies for light and heat". Philosophical Magazine. Series 4, volume 20: 1–21.
- Kirchhoff, G. (1882) , "Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme und Licht", Gessamelte Abhandlungen, Leipzig: Johann Ambrosius Barth, pp. 571–598
- Kondepudi, D.; Prigogine, I. (1998). Modern Thermodynamics. From Heat Engines to Dissipative Structures. John Wiley & Sons. ISBN 0-471-97393-9.
- Kragh, H. (1999). Quantum Generations: a History of Physics in the Twentieth Century. Princeton University Press. ISBN 0-691-01206-7.
- Kuhn, T. S. (1978). Black–Body Theory and the Quantum Discontinuity. Oxford University Press. ISBN 0-19-502383-8.
- Landsberg, P. T. (1990). Thermodynamics and statistical mechanics (Reprint ed.). Courier Dover Publications. ISBN 0-486-66493-7.
- Lavenda, Bernard Howard (1991). Statistical Physics: A Probabilistic Approach. John Wiley & Sons. pp. 41–42. ISBN 978-0-471-54607-8.
- Loudon, R. (2000) . The Quantum Theory of Light (third ed.). Cambridge University Press. ISBN 0-19-850177-3.
- Mandel, L.; Wolf, E. (1995). Optical Coherence and Quantum Optics. Cambridge University Press. ISBN 0-521-41711-2.
- Mehra, J.; Rechenberg, H. (1982). The Historical Development of Quantum Theory. Vol. 1, part 1. Springer-Verlag. ISBN 0-387-90642-8.
- Mihalas, D.; Weibel-Mihalas, B. (1984). Foundations of Radiation Hydrodynamics. Oxford University Press. ISBN 0-19-503437-6.
- Milne, E.A. (1930). "Thermodynamics of the Stars". Handbuch der Astrophysik. 3, part 1: 63–255.
- Müller-Kirsten, Harald J.W. (2013). Basics of Statistical Physics (2nd ed.). World Scientific. ISBN 978-981-4449-53-3.
- Partington, J.R. (1949). An Advanced Treatise on Physical Chemistry. Volume 1. Fundamental Principles. The Properties of Gases. Longmans, Green and Co.
- Planck, M. (1914) . The Theory of Heat Radiation. translated by Masius, M. P. Blakiston's Sons & Co.
- Rybicki, G. B.; Lightman, A. P. (1979). Radiative Processes in Astrophysics. John Wiley & Sons. ISBN 0-471-82759-2.
- Schirrmacher, A. (2001). Experimenting theory: the proofs of Kirchhoff's radiation law before and after Planck. Münchner Zentrum für Wissenschafts und Technikgeschichte.
- Siegel, D.M. (1976). "Balfour Stewart and Gustav Robert Kirchhoff: two independent approaches to "Kirchhoff's radiation law"". Isis. 67 (4): 565–600. doi:10.1086/351669. PMID 794025. S2CID 37368520.
- Stewart, B. (1858). "An account of some experiments on radiant heat". Transactions of the Royal Society of Edinburgh. 22: 1–20. doi:10.1017/S0080456800031288. S2CID 122316368.
- Wien, W. (1894). "Temperatur und Entropie der Strahlung" [Temperature and entropy of radiation]. Annalen der Physik. 288 (5): 132–165. Bibcode:1894AnP...288..132W. doi:10.1002/andp.18942880511.
Further reading
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
- Tipler, Paul; Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman. ISBN 0-7167-4345-0.
External links
- Blackbody radiation JavaScript Interactives Blackbody radiation by Fu-Kwun Hwang and Loo Kang Wee
- Calculating Blackbody Radiation Interactive calculator with Doppler Effect. Includes most systems of units.
- Color-to-Temperature demonstration at Academo.org
- Cooling Mechanisms for Human Body – From Hyperphysics
- Descriptions of radiation emitted by many different objects
- Blackbody Emission Applet Archived 2010-06-09 at the Wayback Machine
- "Blackbody Spectrum" by Jeff Bryant, Wolfram Demonstrations Project, 2007.
 and
and  are very small. In the shorter wavelengths of the ultraviolet range, however, classical theory predicts the energy emitted tends to infinity, hence the ultraviolet catastrophe. The theory even predicted that all bodies would emit most of their energy in the ultraviolet range, clearly contradicted by the experimental data which showed a different peak wavelength at different temperatures (see also
are very small. In the shorter wavelengths of the ultraviolet range, however, classical theory predicts the energy emitted tends to infinity, hence the ultraviolet catastrophe. The theory even predicted that all bodies would emit most of their energy in the ultraviolet range, clearly contradicted by the experimental data which showed a different peak wavelength at different temperatures (see also  where
where
 is the spectral radiance (the
is the spectral radiance (the  radiation per unit
radiation per unit  . Units: power / .
. Units: power / . is the
is the  is the
is the  is the
is the  of emission with respect to the normal. However, this means that, following
of emission with respect to the normal. However, this means that, following  is the radiance density per unit area of emitting surface as the surface area involved in generating the radiance is increased by a factor
is the radiance density per unit area of emitting surface as the surface area involved in generating the radiance is increased by a factor  with respect to an area normal to the propagation direction. At oblique angles, the solid angle spans involved do get smaller, resulting in lower aggregate intensities.
with respect to an area normal to the propagation direction. At oblique angles, the solid angle spans involved do get smaller, resulting in lower aggregate intensities.
 , is related to the photon flux density
, is related to the photon flux density  through
through

 , is a function only of the temperature:
, is a function only of the temperature:
 where the constant b, known as Wien's displacement constant, is equal to
where the constant b, known as Wien's displacement constant, is equal to  2.897771955×10 m K.
2.897771955×10 m K.  is the
is the  In unitless form, the maximum occurs when
In unitless form, the maximum occurs when  , where
, where  . The approximate numerical solution is
. The approximate numerical solution is  . At a typical room temperature of 293 K (20 °C), the maximum intensity is for
. At a typical room temperature of 293 K (20 °C), the maximum intensity is for  over the frequency the radiance
over the frequency the radiance  (units: power / ) is
(units: power / ) is
 by using
by using  with
with  and with
and with  being the
being the  per area
per area  of radiating surface is the useful expression
of radiating surface is the useful expression
 when the receiving surface is perpendicular to the radiation.
when the receiving surface is perpendicular to the radiation.
 for all azimuthal angle (0 to
for all azimuthal angle (0 to  ) and polar angle
) and polar angle  , we arrive at the
, we arrive at the  We used
We used

 Applying the Stefan–Boltzmann law,
Applying the Stefan–Boltzmann law,
 where A and T are the body surface area and temperature,
where A and T are the body surface area and temperature,  is the
is the  The total energy radiated in one day is about 8
The total energy radiated in one day is about 8  For this reason, thermal imaging devices for human subjects are most sensitive in the 7–14 micrometer range.
For this reason, thermal imaging devices for human subjects are most sensitive in the 7–14 micrometer range.

 is the
is the  is the effective temperature of the Sun, and
is the effective temperature of the Sun, and is the radius of the Sun.
is the radius of the Sun.
 is the radius of the planet, and
is the radius of the planet, and is the distance between the
is the distance between the  of this energy where
of this energy where  of the Sun's light, and reflects the rest. The power absorbed by the planet and its atmosphere is then:
of the Sun's light, and reflects the rest. The power absorbed by the planet and its atmosphere is then:

 , it emits in all directions; the spherical surface area being
, it emits in all directions; the spherical surface area being  . If the planet were a perfect black body, it would emit according to the
. If the planet were a perfect black body, it would emit according to the 
 is the temperature of the planet. This temperature, calculated for the case of the planet acting as a black body by setting
is the temperature of the planet. This temperature, calculated for the case of the planet acting as a black body by setting  , is known as the
, is known as the  of the radiation that a black body would emit where
of the radiation that a black body would emit where 


 comes to the same temperature as a black body no matter how dark or light gray.
comes to the same temperature as a black body no matter how dark or light gray.




 set to unity, the
set to unity, the  or −18.8 °C.
or −18.8 °C.
 where v is the velocity of the source in the observer's rest frame, θ is the angle between the velocity vector and the observer-source direction measured in the reference frame of the source, and c is the
where v is the velocity of the source in the observer's rest frame, θ is the angle between the velocity vector and the observer-source direction measured in the reference frame of the source, and c is the  Here v > 0 indicates a receding source, and v < 0 indicates an approaching source.
Here v > 0 indicates a receding source, and v < 0 indicates an approaching source.