| Thermoelectric effect |
|---|
 |
Principles
|
| Applications |
Thermoelectric materials show the thermoelectric effect in a strong or convenient form.
The thermoelectric effect refers to phenomena by which either a temperature difference creates an electric potential or an electric current creates a temperature difference. These phenomena are known more specifically as the Seebeck effect (creating a voltage from temperature difference), Peltier effect (driving heat flow with an electric current), and Thomson effect (reversible heating or cooling within a conductor when there is both an electric current and a temperature gradient). While all materials have a nonzero thermoelectric effect, in most materials it is too small to be useful. However, low-cost materials that have a sufficiently strong thermoelectric effect (and other required properties) are also considered for applications including power generation and refrigeration. The most commonly used thermoelectric material is based on bismuth telluride (Bi
2Te
3).
Thermoelectric materials are used in thermoelectric systems for cooling or heating in niche applications, and are being studied as a way to regenerate electricity from waste heat. Research in the field is still driven by materials development, primarily in optimizing transport and thermoelectric properties.
Thermoelectric figure of merit
The usefulness of a material in thermoelectric systems is determined by the device efficiency. This is determined by the material's electrical conductivity (σ), thermal conductivity (κ), and Seebeck coefficient (S), which change with temperature (T). The maximum efficiency of the energy conversion process (for both power generation and cooling) at a given temperature point in the material is determined by the thermoelectric materials figure of merit , given by
Device efficiency
The efficiency of a thermoelectric device for electricity generation is given by , defined as
The maximum efficiency of a thermoelectric device is typically described in terms of its device figure of merit where the maximum device efficiency is approximately given by where is the fixed temperature at the hot junction, is the fixed temperature at the surface being cooled, and is the mean of and . This maximum efficiency equation is exact when thermoelectric properties are temperature-independent.
For a single thermoelectric leg the device efficiency can be calculated from the temperature dependent properties S, κ and σ and the heat and electric current flow through the material. In an actual thermoelectric device, two materials are used (typically one n-type and one p-type) with metal interconnects. The maximum efficiency is then calculated from the efficiency of both legs and the electrical and thermal losses from the interconnects and surroundings.
Ignoring these losses and temperature dependencies in S, κ and σ, an inexact estimate for is given by where is the electrical resistivity, and the properties are averaged over the temperature range; the subscripts n and p denote properties related to the n- and p-type semiconducting thermoelectric materials, respectively. Only when n and p elements have the same and temperature independent properties () does .
Since thermoelectric devices are heat engines, their efficiency is limited by the Carnot efficiency , the first factor in , while and determines the maximum reversibility of the thermodynamic process globally and locally, respectively. Regardless, the coefficient of performance of current commercial thermoelectric refrigerators ranges from 0.3 to 0.6, one-sixth the value of traditional vapor-compression refrigerators.
Power factor
Often the thermoelectric power factor is reported for a thermoelectric material, given by where S is the Seebeck coefficient, and σ is the electrical conductivity.
Although it is often claimed that TE devices with materials with a higher power factor are able to 'generate' more energy (move more heat or extract more energy from that temperature difference) this is only true for a thermoelectric device with fixed geometry and unlimited heat source and cooling. If the geometry of the device is optimally designed for the specific application, the thermoelectric materials will operate at their peak efficiency which is determined by their not .
Aspects of materials choice
For good efficiency, materials with high electrical conductivity, low thermal conductivity and high Seebeck coefficient are needed.
Electron state density: metals vs semiconductors
The band structure of semiconductors offers better thermoelectric effects than the band structure of metals.
The Fermi energy is below the conduction band causing the state density to be asymmetric around the Fermi energy. Therefore, the average electron energy of the conduction band is higher than the Fermi energy, making the system conducive for charge motion into a lower energy state. By contrast, the Fermi energy lies in the conduction band in metals. This makes the state density symmetric about the Fermi energy so that the average conduction electron energy is close to the Fermi energy, reducing the forces pushing for charge transport. Therefore, semiconductors are ideal thermoelectric materials.
Conductivity
In the efficiency equations above, thermal conductivity and electrical conductivity compete.
The thermal conductivity κ in crystalline solids has mainly two components:
- κ = κ electron + κ phonon
According to the Wiedemann–Franz law, the higher the electrical conductivity, the higher κ electron becomes. Thus in metals the ratio of thermal to electrical conductivity is about fixed, as the electron part dominates. In semiconductors, the phonon part is important and cannot be neglected. It reduces the efficiency. For good efficiency a low ratio of κ phonon / κ electron is desired.
Therefore, it is necessary to minimize κ phonon and keep the electrical conductivity high. Thus semiconductors should be highly doped.
G. A. Slack proposed that in order to optimize the figure of merit, phonons, which are responsible for thermal conductivity must experience the material as a glass (experiencing a high degree of phonon scattering—lowering thermal conductivity) while electrons must experience it as a crystal (experiencing very little scattering—maintaining electrical conductivity): this concept is called phonon glass electron crystal. The figure of merit can be improved through the independent adjustment of these properties.
Quality factor
| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Thermoelectric materials" – news · newspapers · books · scholar · JSTOR (November 2024) (Learn how and when to remove this message) |
The maximum of a material is given by the material's quality factor
where is the Boltzmann constant, is the reduced Planck constant, is the number of degenerated valleys for the band, is the average longitudinal elastic moduli, is the inertial effective mass, is the deformation potential coefficient, is the lattice thermal conduction, and is temperature. The figure of merit, , depends on doping concentration and temperature of the material of interest.
The material quality factor is useful because it allows for an intrinsic comparison of possible efficiency between different materials. This relation shows that improving the electronic component , which primarily affects the Seebeck coefficient, will increase the quality factor of a material. A large density of states can be created due to a large number of conducting bands () or by flat bands giving a high band effective mass (). For isotropic materials . Therefore, it is desirable for thermoelectric materials to have high valley degeneracy in a very sharp band structure. Other complex features of the electronic structure are important. These can be partially quantified using an electronic fitness function.
Materials of interest
Strategies to improve thermoelectric performances include both advanced bulk materials and the use of low-dimensional systems. Such approaches to reduce lattice thermal conductivity fall under three general material types: (1) Alloys: create point defects, vacancies, or rattling structures (heavy-ion species with large vibrational amplitudes contained within partially filled structural sites) to scatter phonons within the unit cell crystal; (2) Complex crystals: separate the phonon glass from the electron crystal using approaches similar to those for superconductors (the region responsible for electron transport should be an electron crystal of a high-mobility semiconductor, while the phonon glass should ideally house disordered structures and dopants without disrupting the electron crystal, analogous to the charge reservoir in high-Tc superconductors); (3) Multiphase nanocomposites: scatter phonons at the interfaces of nanostructured materials, be they mixed composites or thin film superlattices.
Materials under consideration for thermoelectric device applications include:
Bismuth chalcogenides and their nanostructures
Materials such as Bi
2Te
3 and Bi
2Se
3 comprise some of the best performing room temperature thermoelectrics with a temperature-independent figure-of-merit, ZT, between 0.8 and 1.0. Nanostructuring these materials to produce a layered superlattice structure of alternating Bi
2Te
3 and Sb
2Te
3 layers produces a device within which there is good electrical conductivity but perpendicular to which thermal conductivity is poor. The result is an enhanced ZT (approximately 2.4 at room temperature for p-type). Note that this high value of ZT has not been independently confirmed due to the complicated demands on the growth of such superlattices and device fabrication; however the material ZT values are consistent with the performance of hot-spot coolers made out of these materials and validated at Intel Labs.
Bismuth telluride and its solid solutions are good thermoelectric materials at room temperature and therefore suitable for refrigeration applications around 300 K. The Czochralski method has been used to grow single crystalline bismuth telluride compounds. These compounds are usually obtained with directional solidification from melt or powder metallurgy processes. Materials produced with these methods have lower efficiency than single crystalline ones due to the random orientation of crystal grains, but their mechanical properties are superior and the sensitivity to structural defects and impurities is lower due to high optimal carrier concentration.
The required carrier concentration is obtained by choosing a nonstoichiometric composition, which is achieved by introducing excess bismuth or tellurium atoms to primary melt or by dopant impurities. Some possible dopants are halogens and group IV and V atoms. Due to the small bandgap (0.16 eV) Bi2Te3 is partially degenerate and the corresponding Fermi-level should be close to the conduction band minimum at room temperature. The size of the band-gap means that Bi2Te3 has high intrinsic carrier concentration. Therefore, minority carrier conduction cannot be neglected for small stoichiometric deviations. Use of telluride compounds is limited by the toxicity and rarity of tellurium.
Lead tellurides
Heremans et al. (2008) demonstrated that thallium-doped lead telluride alloy (PbTe) achieves a ZT of 1.5 at 773 K. Later, Snyder et al. (2011) reported ZT~1.4 at 750 K in sodium-doped PbTe, and ZT~1.8 at 850 K in sodium-doped PbTe1−xSex alloy. Snyder's group determined that both thallium and sodium alter the electronic structure of the crystal increasing electronic conductivity. They also claim that selenium increases electric conductivity and reduces thermal conductivity.
In 2012 another team used lead telluride to convert waste heat to electricity, reaching a ZT of 2.2, which they claimed was the highest yet reported.
Inorganic clathrates
Inorganic clathrates have the general formula AxByC46-y (type I) and AxByC136-y (type II), where B and C are group III and IV elements, respectively, which form the framework where “guest” A atoms (alkali or alkaline earth metal) are encapsulated in two different polyhedra facing each other. The differences between types I and II come from the number and size of voids present in their unit cells. Transport properties depend on the framework's properties, but tuning is possible by changing the “guest” atoms.
The most direct approach to synthesize and optimize the thermoelectric properties of semiconducting type I clathrates is substitutional doping, where some framework atoms are replaced with dopant atoms. In addition, powder metallurgical and crystal growth techniques have been used in clathrate synthesis. The structural and chemical properties of clathrates enable the optimization of their transport properties as a function of stoichiometry. The structure of type II materials allows a partial filling of the polyhedra, enabling better tuning of the electrical properties and therefore better control of the doping level. Partially filled variants can be synthesized as semiconducting or even insulating.
Blake et al. have predicted ZT~0.5 at room temperature and ZT~1.7 at 800 K for optimized compositions. Kuznetsov et al. measured electrical resistance and Seebeck coefficient for three different type I clathrates above room temperature and by estimating high temperature thermal conductivity from the published low temperature data they obtained ZT~0.7 at 700 K for Ba8Ga16Ge30 and ZT~0.87 at 870 K for Ba8Ga16Si30.
Compounds of Mg and group-14 element
Mg2B (B=Si, Ge, Sn) compounds and their solid solutions are good thermoelectric materials and their ZT values are comparable with those of established materials. The appropriate production methods are based on direct co-melting, but mechanical alloying has also been used. During synthesis, magnesium losses due to evaporation and segregation of components (especially for Mg2Sn) need to be taken into account. Directed crystallization methods can produce single crystals of Mg2Si, but they intrinsically have n-type conductivity, and doping, e.g. with Sn, Ga, Ag or Li, is required to produce p-type material which is required for an efficient thermoelectric device. Solid solutions and doped compounds have to be annealed in order to produce homogeneous samples – with the same properties throughout. At 800 K, Mg2Si0.55−xSn0.4Ge0.05Bix has been reported to have a figure of merit about 1.4, the highest ever reported for these compounds.
Skutterudite thermoelectrics
Skutterudites have a chemical composition of LM4X12, where L is a rare-earth metal (optional component), M is a transition metal, and X is a metalloid, a group V element or a pnictogen such as phosphorus, antimony, or arsenic. These materials exhibit ZT>1.0 and can potentially be used in multistage thermoelectric devices.
Unfilled, these materials contain voids, which can be filled with low-coordination ions (usually rare-earth elements) to reduce thermal conductivity by producing sources for lattice phonon scattering, without reducing electrical conductivity. It is also possible to reduce the thermal conductivity in skutterudite without filling these voids using a special architecture containing nano- and micro-pores.
NASA is developing a Multi-Mission Radioisotope Thermoelectric Generator in which the thermocouples would be made of skutterudite, which can function with a smaller temperature difference than the current tellurium designs. This would mean that an otherwise similar RTG would generate 25% more power at the beginning of a mission and at least 50% more after seventeen years. NASA hopes to use the design on the next New Frontiers mission.
Oxide thermoelectrics
Homologous oxide compounds (such as those of the form (SrTiO
3)n(SrO)
m—the Ruddlesden-Popper phase) have layered superlattice structures that make them promising candidates for use in high-temperature thermoelectric devices. These materials exhibit low thermal conductivity perpendicular to the layers while maintaining good electronic conductivity within the layers. Their ZT values can reach 2.4 for epitaxial SrTiO
3 films, and the enhanced thermal stability of such oxides, as compared to conventional high-ZT bismuth compounds, makes them superior high-temperature thermoelectrics.
Interest in oxides as thermoelectric materials was reawakened in 1997 when a relatively high thermoelectric power was reported for NaCo2O4. In addition to their thermal stability, other advantages of oxides are their low toxicity and high oxidation resistance. Simultaneously controlling both the electric and phonon systems may require nanostructured materials. Layered Ca3Co4O9 exhibited ZT values of 1.4–2.7 at 900 K. If the layers in a given material have the same stoichiometry, they will be stacked so that the same atoms will not be positioned on top of each other, impeding phonon conductivity perpendicular to the layers. Recently, oxide thermoelectrics have gained a lot of attention so that the range of promising phases increased drastically. Novel members of this family include ZnO, MnO2, and NbO2.
Cation-substituted copper sulfide thermoelectrics
All variables mentioned are included in the equation for the dimensionless figure of merit, zT, which can be seen at the top of this page. The goal of any thermoelectric experiment is to make the power factor, S σ, larger while maintaining a small thermal conductivity. This is because electricity is produced through a temperature gradient, so materials that can equilibrate heat very quickly are not useful. The two compounds detailed below were found to exhibit high-performing thermoelectric properties, which can be evidenced by the reported figure of merit in either respective manuscript.
Cuprokalininite (CuCr2S4) is a copper-dominant analogue of the mineral joegoldsteinite. It was recently found within metamorphic rocks in Slyudyanka, part of the South Baikal region of Russia, and researchers have determined that Sb-doped cuprokalininite (Cu1-xSbxCr2S4) shows promise in renewable technology. Doping is the act of intentionally adding an impurity, usually to modify the electrochemical characteristics of the seed material. The introduction of antimony enhances the power factor by bringing in extra electrons, which increases the Seebeck coefficient, S, and reduces the magnetic moment (how likely the particles are to align with a magnetic field); it also distorts the crystal structure, which lowers the thermal conductivity, κ. Khan et al. (2017) were able to discover the optimal amount of Sb content (x=0.3) in cuprokalininte in order to develop a device with a ZT value of 0.43.
Bornite (Cu5FeS4) is a sulfide mineral named after an Austrian mineralogist, though it is much more common than the aforementioned cuprokalininite. This metal ore was found to demonstrate an improved thermoelectric performance after undergoing cation exchange with iron. Cation exchange is the process of surrounding a parent crystal with an electrolyte complex, so that the cations (positively charged ions) within the structure can be swapped out for those in solution without affecting the anion sublattice (negatively charged crystal network). What one is left with are crystals that possess a different composition, yet an identical framework. In this way, scientists are granted extreme morphological control and uniformity when generating complicated heterostructures. As to why it was thought to improve the ZT value, the mechanics of cation exchange often bring about crystallographic defects, which cause phonons (simply put, heat particles) to scatter. According to the Debye-Callaway formalism, a model used to determine the lattice thermal conductivity, κL, the highly anharmonic behavior due to phonon scattering results in a large thermal resistance. Therefore, a greater defect density decreases the lattice thermal conductivity, thereby making a larger figure of merit. In conclusion, Long et al. reported that greater Cu-deficiencies resulted in increases of up to 88% in the ZT value, with a maximum of 0.79.
The composition of thermoelectric devices can dramatically vary depending on the temperature of the heat they must harvest; considering the fact that more than eighty percent of industry waste falls within a range of 373-575 K, chalcogenides and antimonides are better suited for thermoelectric conversion because they can utilize heat at lower temperatures. Not only is sulfur the cheapest and lightest chalcogenide, current surpluses may be causing threat to the environment since it is a byproduct of oil capture, so sulfur consumption could help mitigate future damage. As for the metal, copper is an ideal seed particle for any kind of substitution method because of its high mobility and variable oxidation state, for it can balance or complement the charge of more inflexible cations. Therefore, either the cuprokalininite or bornite minerals could prove ideal thermoelectric components.
Half-Heusler alloys
Half-Heusler (HH) alloys have a great potential for high-temperature power generation applications. Examples of these alloys include NbFeSb, NbCoSn and VFeSb. They have a cubic MgAgAs-type structure formed by three interpenetrating face-centered-cubic (fcc) lattices. The ability to substitute any of these three sublattices opens the door for wide variety of compounds to be synthesized. Various atomic substitutions are employed to reduce the thermal conductivity and enhance the electrical conductivity.
Previously, ZT could not peak more than 0.5 for p-type and 0.8 for n-type HH compound. However, in the past few years, researchers were able to achieve ZT≈1 for both n-type and p-type. Nano-sized grains is one of the approaches used to lower the thermal conductivity via grain boundaries- assisted phonon scattering. Other approach was to utilize the principles of nanocomposites, by which certain combination of metals were favored on others due to the atomic size difference. For instance, Hf and Ti is more effective than Hf and Zr, when reduction of thermal conductivity is of concern, since the atomic size difference between the former is larger than that of the latter.
Flexible Thermoelectric Materials
Electrically conducting organic materials


Conducting polymers are of significant interest for flexible thermoelectric development. They are flexible, lightweight, geometrically versatile, and can be processed at scale, an important component for commercialization. However, the structural disorder of these materials often inhibits the electrical conductivity much more than the thermal conductivity, limiting their use so far. Some of the most common conducting polymers investigated for flexible thermoelectrics include poly(3,4-ethylenedioxythiophene) (PEDOT), polyanilines (PANIs), polythiophenes, polyacetylenes, polypyrrole, and polycarbazole. P-type PEDOT:PSS (polystyrene sulfonate) and PEDOT-Tos (Tosylate) have been some of the most encouraging materials investigated. Organic, air-stable n-type thermoelectrics are often harder to synthesize because of their low electron affinity and likelihood of reacting with oxygen and water in the air. These materials often have a figure of merit that is still too low for commercial applications (~0.42 in PEDOT:PSS) due to the poor electrical conductivity.
Hybrid Composites
Hybrid composite thermoelectrics involve blending the previously discussed electrically conducting organic materials or other composite materials with other conductive materials in an effort to improve transport properties. The conductive materials that are most commonly added include carbon nanotubes and graphene due to their conductivities and mechanical properties. It has been shown that carbon nanotubes can increase the tensile strength of the polymer composite they are blended with. However, they can also reduce the flexibility. Furthermore, future study into the orientation and alignment of these added materials will allow for improved performance. The percolation threshold of CNT’s is often especially low, well below 10%, due to their high aspect ratio. A low percolation threshold is desirable for both cost and flexibility purposes. Reduced graphene oxide (rGO) as graphene-related material was also used to enhance figure of merit of thermoelectric materials. The addition of rather low amount of graphene or rGO around 1 wt% mainly strengthens the phonon scattering at grain boundaries of all these materials as well as increases the charge carrier concentration and mobility in chalcogenide-, skutterudite- and, particularly, metal oxide-based composites. However, significant growth of ZT after addition of graphene or rGO was observed mainly for composites based on thermoelectric materials with low initial ZT. When thermoelectric material is already nanostructured and possesses high electrical conductivity, such an addition does not enhance ZT significantly. Thus, graphene or rGO-additive works mainly as an optimizer of the intrinsic performance of thermoelectric materials.
Hybrid thermoelectric composites also refer to polymer-inorganic thermoelectric composites. This is generally achieved through an inert polymer matrix that is host to thermoelectric filler material. The matrix is generally nonconductive so as to not short current as well as to let the thermoelectric material dominate electrical transport properties. One major benefit of this method is that the polymer matrix will generally be highly disordered and random on many different length scales, meaning that the composite material will can have a much lower thermal conductivity. The general procedure to synthesize these materials involves a solvent to dissolve the polymer and dispersion of the thermoelectric material throughout the mixture.
Silicon-germanium alloys
Bulk Si exhibits a low ZT of ~0.01 because of its high thermal conductivity. However, ZT can be as high as 0.6 in silicon nanowires, which retain the high electrical conductivity of doped Si, but reduce the thermal conductivity due to elevated scattering of phonons on their extensive surfaces and low cross-section.
Combining Si and Ge also allows to retain a high electrical conductivity of both components and reduce the thermal conductivity. The reduction originates from additional scattering due to very different lattice (phonon) properties of Si and Ge. As a result, Silicon-germanium alloys are currently the best thermoelectric materials around 1000 °C and are therefore used in some radioisotope thermoelectric generators (RTG) (notably the MHW-RTG and GPHS-RTG) and some other high^temperature applications, such as waste heat recovery. Usability of silicon-germanium alloys is limited by their high price and moderate ZT values (p-SiGe ~0.7 and n-SiGe ~1.0); however, ZT can be increased to 1–2 in SiGe nanostructures owing to the reduction in thermal conductivity.
Sodium cobaltate
Experiments on crystals of sodium cobaltate, using X-ray and neutron scattering experiments carried out at the European Synchrotron Radiation Facility (ESRF) and the Institut Laue-Langevin (ILL) in Grenoble were able to suppress thermal conductivity by a factor of six compared to vacancy-free sodium cobaltate. The experiments agreed with corresponding density functional calculations. The technique involved large anharmonic displacements of Na
0.8CoO
2 contained within the crystals.
Amorphous materials
In 2002, Nolas and Goldsmid have come up with a suggestion that systems with the phonon mean free path larger than the charge carrier mean free path can exhibit an enhanced thermoelectric efficiency. This can be realized in amorphous thermoelectrics and soon they became a focus of many studies. This ground-breaking idea was accomplished in Cu-Ge-Te, NbO2, In-Ga-Zn-O, Zr-Ni-Sn, Si-Au, and Ti-Pb-V-O amorphous systems. It should be mentioned that modelling of transport properties is challenging enough without breaking the long-range order so that design of amorphous thermoelectrics is at its infancy. Naturally, amorphous thermoelectrics give rise to extensive phonon scattering, which is still a challenge for crystalline thermoelectrics. A bright future is expected for these materials.
Functionally graded materials
Functionally graded materials make it possible to improve the conversion efficiency of existing thermoelectrics. These materials have a non-uniform carrier concentration distribution and in some cases also solid solution composition. In power generation applications the temperature difference can be several hundred degrees and therefore devices made from homogeneous materials have some part that operates at the temperature where ZT is substantially lower than its maximum value. This problem can be solved by using materials whose transport properties vary along their length thus enabling substantial improvements to the operating efficiency over large temperature differences. This is possible with functionally graded materials as they have a variable carrier concentration along the length of the material, which is optimized for operations over specific temperature range.
Nanomaterials and superlattices
In addition to nanostructured Bi
2Te
3/Sb
2Te
3 superlattice thin films, other nanostructured materials, including silicon nanowires, nanotubes and quantum dots show potential in improving thermoelectric properties.
PbTe/PbSeTe quantum dot superlattice
Another example of a superlattice involves a PbTe/PbSeTe quantum dot superlattices provides an enhanced ZT (approximately 1.5 at room temperature) that was higher than the bulk ZT value for either PbTe or PbSeTe (approximately 0.5).
Nanocrystal stability and thermal conductivity
Main article: Microstructurally stable nanocrystalline alloysNot all nanocrystalline materials are stable, because the crystal size can grow at high temperatures, ruining the materials' desired characteristics.
Nanocrystalline materials have many interfaces between crystals, which Physics of SASER scatter phonons so the thermal conductivity is reduced. Phonons are confined to the grain, if their mean free path is larger than the material grain size.
Nanocrystalline transition metal silicides
Nanocrystalline transition metal silicides are a promising material group for thermoelectric applications, because they fulfill several criteria that are demanded from the commercial applications point of view. In some nanocrystalline transition metal silicides the power factor is higher than in the corresponding polycrystalline material but the lack of reliable data on thermal conductivity prevents the evaluation of their thermoelectric efficiency.
Nanostructured skutterudites
Skutterudites, a cobalt arsenide mineral with variable amounts of nickel and iron, can be produced artificially, and are candidates for better thermoelectric materials.
One advantage of nanostructured skutterudites over normal skutterudites is their reduced thermal conductivity, caused by grain boundary scattering. ZT values of ~0.65 and > 0.4 have been achieved with CoSb3 based samples; the former values were 2.0 for Ni and 0.75 for Te-doped material at 680 K and latter for Au-composite at T > 700 K.
Even greater performance improvements can be achieved by using composites and by controlling the grain size, the compaction conditions of polycrystalline samples and the carrier concentration.
Graphene
Graphene is known for its high electrical conductivity and Seebeck coefficient at room temperature. However, from thermoelectric perspective, its thermal conductivity is notably high, which in turn limits its ZT. Several approaches were suggested to reduce the thermal conductivity of graphene without altering much its electrical conductivity. These include, but not limited to, the following:
- Doping with carbon isotopes to form isotopic heterojunction such as that of C and C. Those isotopes possess different phonon frequency mismatch, which leads to the scattering of the heat carriers (phonons). This approach has been shown to affect neither the power factor nor the electrical conductivity.
- Wrinkles and cracks in the graphene structure were shown to contribute to the reduction in the thermal conductivity. Reported values of thermal conductivity of suspended graphene of size 3.8 μm show a wide spread from 1500 to 5000 W/(m·K). A recent study attributed that to the microstructural defects present in graphene, such as wrinkles and cracks, which can drop the thermal conductivity by 27%. These defects help scatter phonons.
- Introduction of defects with techniques such as oxygen plasma treatment. A more systemic way of introducing defects in graphene structure is done through O2 plasma treatment. Ultimately, the graphene sample will contain prescribed-holes spaced and numbered according to the plasma intensity. People were able to improve ZT of graphene from 1 to a value of 2.6 when the defect density is raised from 0.04 to 2.5 (this number is an index of defect density and usually understood when compared to the corresponding value of the un-treated graphene, 0.04 in our case). Nevertheless, this technique would lower the electrical conductivity as well, which can be kept unchanged if the plasma processing parameters are optimized.
- Functionalization of graphene by oxygen. The thermal behavior of graphene oxide has not been investigated extensively as compared to its counterpart; graphene. However, it was shown theoretically by Density Functional Theory (DFT) model that adding oxygen into the lattice of graphene reduces a lot its thermal conductivity due to phonon scattering effect. Scattering of phonons result from both acoustic mismatch and reduced symmetry in graphene structure after doping with oxygen. The reduction of thermal conductivity can easily exceed 50% with this approach.
Superlattices and roughness
Superlattices – nano structured thermocouples, are considered a good candidate for better thermoelectric device manufacturing, with materials that can be used in manufacturing this structure.
Their production is expensive for general-use due to fabrication processes based on expensive thin-film growth methods. However, since the amount of thin-film materials required for device fabrication with superlattices, is so much less than thin-film materials in bulk thermoelectric materials (almost by a factor of 1/10,000) the long-term cost advantage is indeed favorable.
This is particularly true given the limited availability of tellurium causing competing solar applications for thermoelectric coupling systems to rise.
Superlattice structures also allow the independent manipulation of transport parameters by adjusting the structure itself, enabling research for better understanding of the thermoelectric phenomena in nanoscale, and studying the phonon-blocking electron-transmitting structures – explaining the changes in electric field and conductivity due to the material's nano-structure.
Many strategies exist to decrease the superlattice thermal conductivity that are based on engineering of phonon transport. The thermal conductivity along the film plane and wire axis can be reduced by creating diffuse interface scattering and by reducing the interface separation distance, both which are caused by interface roughness.
Interface roughness can naturally occur or may be artificially induced. In nature, roughness is caused by the mixing of atoms of foreign elements. Artificial roughness can be created using various structure types, such as quantum dot interfaces and thin-films on step-covered substrates.
Problems in superlattices
Reduced electrical conductivity:
Reduced phonon-scattering interface structures often also exhibit a decrease in electrical conductivity.
The thermal conductivity in the cross-plane direction of the lattice is usually very low, but depending on the type of superlattice, the thermoelectric coefficient may increase because of changes to the band structure.
Low thermal conductivity in superlattices is usually due to strong interface scattering of phonons. Minibands are caused by the lack of quantum confinement within a well. The mini-band structure depends on the superlattice period so that with a very short period (~1 nm) the band structure approaches the alloy limit and with a long period (≥ ~60 nm) minibands become so close to each other that they can be approximated with a continuum.
Superlattice structure countermeasures:
Counter measures can be taken which practically eliminate the problem of decreased electrical conductivity in a reduced phonon-scattering interface. These measures include the proper choice of superlattice structure, taking advantage of mini-band conduction across superlattices, and avoiding quantum-confinement. It has been shown that because electrons and phonons have different wavelengths, it is possible to engineer the structure in such a way that phonons are scattered more diffusely at the interface than electrons.
Phonon confinement countermeasures:
Another approach to overcome the decrease in electrical conductivity in reduced phonon-scattering structures is to increase phonon reflectivity and therefore decrease the thermal conductivity perpendicular to the interfaces.
This can be achieved by increasing the mismatch between the materials in adjacent layers, including density, group velocity, specific heat, and the phonon-spectrum.
Interface roughness causes diffuse phonon scattering, which either increases or decreases the phonon reflectivity at the interfaces. A mismatch between bulk dispersion relations confines phonons, and the confinement becomes more favorable as the difference in dispersion increases.
The amount of confinement is currently unknown as only some models and experimental data exist. As with a previous method, the effects on the electrical conductivity have to be considered.
Attempts to localize long-wavelength phonons by aperiodic superlattices or composite superlattices with different periodicities have been made. In addition, defects, especially dislocations, can be used to reduce thermal conductivity in low dimensional systems.
Parasitic heat:
Parasitic heat conduction in the barrier layers could cause significant performance loss. It has been proposed but not tested that this can be overcome by choosing a certain correct distance between the quantum wells.
The Seebeck coefficient can change its sign in superlattice nanowires due to the existence of minigaps as Fermi energy varies. This indicates that superlattices can be tailored to exhibit n or p-type behavior by using the same dopants as those that are used for corresponding bulk materials by carefully controlling Fermi energy or the dopant concentration. With nanowire arrays, it is possible to exploit semimetal-semiconductor transition due to the quantum confinement and use materials that normally would not be good thermoelectric materials in bulk form. Such elements are for example bismuth. The Seebeck effect could also be used to determine the carrier concentration and Fermi energy in nanowires.
In quantum dot thermoelectrics, unconventional or nonband transport behavior (e.g. tunneling or hopping) is necessary to utilize their special electronic band structure in the transport direction. It is possible to achieve ZT>2 at elevated temperatures with quantum dot superlattices, but they are almost always unsuitable for mass production.
However, in superlattices, where quantum-effects are not involved, with film thickness of only a few micrometers (μm) to about 15 μm, Bi2Te3/Sb2Te3 superlattice material has been made into high-performance microcoolers and other devices. The performance of hot-spot coolers are consistent with the reported ZT~2.4 of superlattice materials at 300 K.
Nanocomposites are promising material class for bulk thermoelectric devices, but several challenges have to be overcome to make them suitable for practical applications. It is not well understood why the improved thermoelectric properties appear only in certain materials with specific fabrication processes.
SrTe nanocrystals can be embedded in a bulk PbTe matrix so that rocksalt lattices of both materials are completely aligned (endotaxy) with optimal molar concentration for SrTe only 2%. This can cause strong phonon scattering but would not affect charge transport. In such case, ZT~1.7 can be achieved at 815 K for p-type material.
Tin selenide
In 2014, researchers at Northwestern University discovered that tin selenide (SnSe) has a ZT of 2.6 along the b axis of the unit cell. This was the highest value reported to date. This was attributed to an extremely low thermal conductivity found in the SnSe lattice. Specifically, SnSe demonstrated a lattice thermal conductivity of 0.23 W·m·K, much lower than previously reported values of 0.5 W·m·K and greater. This material also exhibited a ZT of 2.3±0.3 along the c-axis and 0.8±0.2 along the a-axis. These results were obtained at a temperature of 923 K (650 °C). As shown by the figures below, SnSe performance metrics were found to significantly improve at higher temperatures; this is due to a structural change. Power factor, conductivity, and thermal conductivity all reach their optimal values at or above 750 K, and appear to plateau at higher temperatures. However, other groups have not been able to reproduce the reported bulk thermal conductivity data.
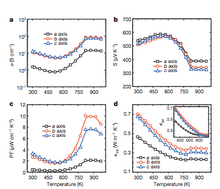
Although it exists at room temperature in an orthorhombic structure with space group Pnma, SnSe undergoes a transition to a structure with higher symmetry, space group Cmcm, at higher temperatures. This structure consists of Sn-Se planes that are stacked upwards in the a-direction, which accounts for the poor performance out-of-plane (along a-axis). Upon transitioning to the Cmcm structure, SnSe maintains its low thermal conductivity but exhibits higher carrier mobilities.
One impediment to further development of SnSe is that it has a relatively low carrier concentration: approximately 10 cm. Compounding this issue is the fact that SnSe has been reported to have low doping efficiency.
However, such single crystalline materials suffer from inability to make useful devices due to their brittleness as well as narrow range of temperatures, where ZT is reported to be high.
In 2021 the researchers announced a polycrystalline form of SnSe that was at once less brittle and featured a ZT of 3.1.
Anderson localization
Anderson localization is a quantum mechanical phenomenom where charge carriers in a random potential are trapped in place (i.e. they are in localized states as opposed to being in scattering states if they could move freely). This localization prevents the charge carriers from moving, which inhibits their contribution to the thermal conductivity of a material, but because it also lowers the electrical conductivity, it was thought to reduce ZT and be detrimental for thermoelectric materials. In 2019, it was proposed that by localizing only the minority charge carriers in a doped semiconductor (i.e. holes in an n-doped semiconductor or electrons in a p-doped semiconductor), Anderson localization could increase ZT. The heat conductivity associated with movement of the minority charge carriers would be reduced while electrical conductivity of the majority charge carrier would be unaffected.
In 2020, researchers at Kyung Hee University demonstrated the use of Anderson localization in an n-type semiconductor to improve the thermoelectric properties of a material. They embedded nanoparticles of silver telluride (Ag2Te) in a lead telluride (PbTe) matrix. Ag2Te undergoes a phase transition around 407 K. Below this temperature, both holes and electrons are localized at the Ag2Te nanoparticles, while after the transition, holes are still localized, but electrons can move freely in the material. The researchers were able to increase ZT from 1.5 to above 2.0 using this method.
Production methods
Production methods for these materials can be divided into powder and crystal growth based techniques. Powder based techniques offer excellent ability to control and maintain desired carrier distribution, particle size, and composition. In crystal growth techniques dopants are often mixed with melt, but diffusion from gaseous phase can also be used. In the zone melting techniques disks of different materials are stacked on top of others and then materials are mixed with each other when a traveling heater causes melting. In powder techniques, either different powders are mixed with a varying ratio before melting or they are in different layers as a stack before pressing and melting.
There are applications, such as cooling of electronic circuits, where thin films are required. Therefore, thermoelectric materials can also be synthesized using physical vapor deposition techniques. Another reason to utilize these methods is to design these phases and provide guidance for bulk applications.
3D Printing
Significant improvement on 3D printing skills has made it possible for thermoelectric components to be prepared via 3D printing. Thermoelectric products are made from special materials that absorb heat and create electricity. The requirement of fitting complex geometries in tightly constrained spaces makes 3D printing the ideal manufacturing technique. There are several benefits to the use of additive manufacturing in thermoelectric material production. Additive manufacturing allows for innovation in the design of these materials, facilitating intricate geometries that would not otherwise be possible by conventional manufacturing processes. It reduces the amount of wasted material during production and allows for faster production turnaround times by eliminating the need for tooling and prototype fabrication, which can be time-consuming and expensive.
There are several major additive manufacturing technologies that have emerged as feasible methods for the production of thermoelectric materials, including continuous inkjet printing, dispenser printing, screen printing, stereolithography, and selective laser sintering. Each method has its own challenges and limitations, especially related to the material class and form that can be used. For example, selective laser sintering (SLS) can be used with metal and ceramic powders, stereolithography (SLA) must be used with curable resins containing solid particle dispersions of the thermoelectric material of choice, and inkjet printing must use inks which are usually synthesized by dispersing inorganic powders to organic solvent or making a suspension.
The motivation for producing thermoelectrics by means of additive manufacturing is due to a desire to improve the properties of these materials, namely increasing their thermoelectric figure of merit ZT, and thereby improving their energy conversion efficiency. Research has been done proving the efficacy and investigating the material properties of thermoelectric materials produced via additive manufacturing. An extrusion-based additive manufacturing method was used to successfully print bismuth telluride (Bi2Te3) with various geometries. This method utilized an all-inorganic viscoelastic ink synthesized using Sb2Te2 chalcogenidometallate ions as binders for Bi2Te3-based particles. The results of this method showed homogenous thermoelectric properties throughout the material and a thermoelectric figure of merit ZT of 0.9 for p-type samples and 0.6 for n-type samples. The Seebeck coefficient of this material was also found to increase with increasing temperature up to around 200 °C.
Groundbreaking research has also been done towards the use of selective laser sintering (SLS) for the production of thermoelectric materials. Loose Bi2Te3 powders have been printed via SLS without the use of pre- or post-processing of the material, pre-forming of a substrate, or use of binder materials. The printed samples achieved 88% relative density (compared to a relative density of 92% in conventionally manufactured Bi2Te3). Scanning Electron Microscopy (SEM) imaging results showed adequate fusion between layers of deposited materials. Though pores existed within the melted region, this is a general existing issue with parts made by SLS, occurring as a result of gas bubbles that get trapped in the melted material during its rapid solidification. X-ray diffraction results showed that the crystal structure of the material was intact after laser melting.
The Seebeck coefficient, figure of merit ZT, electrical and thermal conductivity, specific heat, and thermal diffusivity of the samples were also investigated, at high temperatures up to 500 °C. Of particular interest is the ZT of these Bi2Te3 samples, which were found to decrease with increasing temperatures up to around 300 °C, increase slightly at temperatures between 300-400 °C, and then increase sharply without further increase in temperature. The highest achieved ZT value (for an n-type sample) was about 0.11.
The bulk thermoelectric material properties of samples produced using SLS had comparable thermoelectric and electrical properties to thermoelectric materials produced using conventional manufacturing methods. This the first time the SLS method of thermoelectric material production has been used successfully.
Mechanical Properties
Thermoelectric materials are commonly used in thermoelectric generators to convert the thermal energy into electricity. Thermoelectric generators have the advantage of no moving parts and do not require any chemical reaction for energy conversion, which make them stand out from other sustainable energy resources such as wind turbine and solar cells; Nevertheless, the mechanical performance of thermoelectric generators may decay over time due to plastic, fatigue and creep deformation as a result of being subjected to complex and time-varying thermomechanical stresses.
Thermomechanical Stresses in Thermoelectric Devices
Geometrical Effects
In their research, Al-Merbati et al. found that the stress levels around the leg corners of thermoelectric devices were high and generally increased closer to the hot side. However, switching to a trapezoidal leg geometry reduced thermal stresses. Erturun et al. compared various leg geometries and discovered that rectangular prism and cylindrical legs experienced the highest stresses. Studies have also shown that using thinner and longer legs can significantly relieve stress. Tachibana and Fang estimated the relationship between thermal stress, temperature difference, coefficient of thermal expansion, and module dimensions. They found that the thermal stress was proportional to, where L, α, ΔT and h are module thickness, Coefficients of Thermal Expansion(CTE), temperature difference and leg height, respectively.
Effect of Boundary Conditions
Clin et al. conducted finite-element analysis to replicate thermal stresses in a thermoelectric module and concluded that the thermal stresses were dependent on the mechanical boundary conditions on the module and on CTE mismatch between various components. The corners of the legs exhibited maximum stresses. In a separate investigation, Turenne et al. examined the distribution of stress in large freestanding thermoelectric modules and those rigidly fixed between two surfaces for thermal exchange. Although boundary conditions significantly altered the stress distribution, the authors deduced that external compressive loading on the TE module resulted in the creation of global compressive stresses.
Effect of Thermal Fatigue
Thermoelectric materials commonly contain different types of defects, such as dislocations, vacancies, secondary phases and antisite defects. These defects can affect thermoelectric performance by evolving under service conditions. In 2019, Yun Zheng et al. studied thermal fatigue of -based materials and they proposed that their fatigue behavior can be reduced via boosting the fracture toughness by introducing pores, microcracks or inclusion with the inextricable trade-off with fracture strength.
Effect of Thermal Shocks
Thermoelectric materials can undergo thermal shock loading through service temperature spikes, soldering and metallizing processes. The thermoelectric leg can be coated with metals to form the required diffusion barrier (Metallizing) and dipping the metallized leg in a molten alloy bath (Soldering) for connecting the leg to the interconnect. In a study conducted by Pelletier et al. thermoelectric disks were quenched for the purpose of thermal shock experiments. They realized that quenching in a hot medium helped disks' surface to produce compressive stresses in contrary to the core, which developed tensile stress. Anisotropic materials and thin disks were reported to develop greater maximum stresses. They also observed fracturing of specimens during quenching process in a soldering bath from room temperature.
Effect of Tensile Stresses
Thermal stresses have been quantified and extensively studied in thermoelectric modules throughout the years but von Mises stresses are commonly reported. The von Mises stress defines a constraint on plastic yielding without having any information of the stress nature.
For instance, in a study by Sakamoto et al. the mechanical stability of a -based structure was investigated that could utilize thermoelectric legs at an angle with elecftrical interconnects and substrates. Maximum tensile strength stresses were calculated and compared to the ultimate tensile strength of different materials. This approach might be misleading for brittle materials (such as ceramics) as they do not possess a defined tensile strength.
Thermal Mismatch Stresses
In 2018, Chen et al. investigated the cracking failure of Cu pillar bump that was caused by electromigration under thermoelectric coupling load. They showed that under thermoelectric coupling load, will experience severe joule heat and current density that can be accumulate thermoemechanical stress and miscrostructure evolution. They also pointed out that the difference in CTE between materials in the flip chip package causes thermal mismatch stress which can later develop the cavities to expand along cathode into cracks. Also, it is worth noting that they mentioned thermal-electrical coupling can cause electromigration, microcracks and delamination due to temperature and stress concentration that can fail Cu pillar bumps.
Phase-Transformation Stresses
Phase transformation can occur in thermoelectric materials as well as many other energy materials. As pointed out by Al Malki et al., phase transformation can lead to a total plastic strain when internal mismatch stresses are biased with shear stress. The alpha phase of transforms to a body centered cubic phase. Liang et al. showed that a crack was observed when heating through 407 K through this phase transformation.
Creep Deformation
Creep deformation is a time-dependent mechanism where strain accumulates as amaterial is subjected to external or internal stressesat a high homologous temperature in excess ofT/Tm= 0.5(whereTmis the melting point in K). This phenomenon can emerge in thermoelectric devices after operating for a long time (i.e. months to years). A coarse-grained or monocrystalline structures have been shown to be desirable as creep-resistant materials.
Applications
Refrigeration
Main article: Thermoelectric coolingThermoelectric materials can be used as refrigerators, called "thermoelectric coolers", or "Peltier coolers" after the Peltier effect that controls their operation. As a refrigeration technology, Peltier cooling is far less common than vapor-compression refrigeration. The main advantages of a Peltier cooler (compared to a vapor-compression refrigerator) are its lack of moving parts or refrigerant, and its small size and flexible shape (form factor).
The main disadvantage of Peltier coolers is low efficiency. It is estimated that materials with ZT>3 (about 20–30% Carnot efficiency) would be required to replace traditional coolers in most applications. Today, Peltier coolers are only used in niche applications, especially small scale, where efficiency is not important.
Power generation
Main article: Thermoelectric generatorThermoelectric efficiency depends on the figure of merit, ZT. There is no theoretical upper limit to ZT, and as ZT approaches infinity, the thermoelectric efficiency approaches the Carnot limit. However, until recently no known thermoelectrics had a ZT>3. In 2019, researchers reported a material with approximated ZT between 5 and 6.
As of 2010, thermoelectric generators serve application niches where efficiency and cost are less important than reliability, light weight, and small size.
Internal combustion engines capture 20–25% of the energy released during fuel combustion. Increasing the conversion rate can increase mileage and provide more electricity for on-board controls and creature comforts (stability controls, telematics, navigation systems, electronic braking, etc.) It may be possible to shift energy draw from the engine (in certain cases) to the electrical load in the car, e.g., electrical power steering or electrical coolant pump operation.
Cogeneration power plants use the heat produced during electricity generation for alternative purposes; being this more profitable in industries with high amounts of waste energy.
Thermoelectrics may find applications in such systems or in solar thermal energy generation.
See also
References
- ^ Goldsmid, H. Julian (2016). Introduction to Thermoelectricity. Springer Series in Materials Science. Vol. 121. Berlin, Heidelberg: Springer Berlin Heidelberg. Bibcode:2016inh..book.....G. doi:10.1007/978-3-662-49256-7. ISBN 978-3-662-49255-0.
- Snyder, G.J.; Toberer, E.S. (2008). "Complex Thermoelectric Materials". Nature Materials. 7 (2): 105–114. Bibcode:2008NatMa...7..105S. doi:10.1038/nmat2090. PMID 18219332.
- Wang, H; Pei, Y; LaLonde, AD; Snyder, GJ (2012). "Weak electron-phonon coupling contributing to high thermoelectric performance in n-type PbSe". Proc Natl Acad Sci U S A. 109 (25): 9705–9. Bibcode:2012PNAS..109.9705W. doi:10.1073/pnas.1111419109. PMC 3382475. PMID 22615358.
- Nolas, G.S.; Sharp, J.; Goldsmid, H.J. (2001). Thermoelectrics: basic principles and new materials developments. Springer Series in Materials Science. Vol. 45. Berlin, Heidelberg: Springer- Verlag Berlin Heidelberg New York. doi:10.1007/978-3-662-04569-5. ISBN 3-540-41245-X.
- ^ Ioffe, A.F. (1960) Physics of semiconductors, Academic Press Inc., New York
- M., Borrego, Jose (1962). Optimum impurity concentration in semiconductor thermoelements. Massachusetts Institute of Technology, Energy Conversion and Semiconductor Laboratory, Electrical Engineering Dept. OCLC 16320521.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Kim, Hee Seok; Liu, Weishu; Chen, Gang; Chu, Ching-Wu; Ren, Zhifeng (2015). "Relationship between thermoelectric figure of merit and energy conversion efficiency". Proceedings of the National Academy of Sciences. 112 (27): 8205–8210. Bibcode:2015PNAS..112.8205K. doi:10.1073/pnas.1510231112. PMC 4500231. PMID 26100905.
- Snyder, G.J. (2017). "Figure of merit ZT of a thermoelectric device defined from materials properties". Energy and Environmental Science. 10 (11): 2280–2283. doi:10.1039/C7EE02007D.
- Sherman, B.; Heikes, R. R.; Ure, R. W. (Jan 1960). "Calculation of Efficiency of Thermoelectric Devices". Journal of Applied Physics. 31 (1): 1–16. Bibcode:1960JAP....31....1S. doi:10.1063/1.1735380. ISSN 0021-8979.
- Kim, Hee Seok; Liu, Weishu; Chen, Gang; Chu, Ching-Wu; Ren, Zhifeng (2015-07-07). "Relationship between thermoelectric figure of merit and energy conversion efficiency". Proceedings of the National Academy of Sciences. 112 (27): 8205–8210. Bibcode:2015PNAS..112.8205K. doi:10.1073/pnas.1510231112. ISSN 0027-8424. PMC 4500231. PMID 26100905.
- Kim, D.S.; Infante Ferreira, C.A. (2008). "Solar refrigeration options – a state-of-the-art review". International Journal of Refrigeration. 31: 3–15. doi:10.1016/j.ijrefrig.2007.07.011.
- Baranowski, L.L.; Toberer, E.S.; Snyder, GJ (2013). "The Misconception of Maximum Power and Power Factor in Thermoelectrics" (PDF). Journal of Applied Physics. 115: 126102. doi:10.1063/1.4869140.
- ^ Timothy D. Sands (2005), Designing Nanocomposite Thermoelectric Materials
- Slack GA., in Rowe 2018
- Mahan, G. D. (1997). "Good Thermoelectrics". Solid State Physics - Advances in Research and Applications. Vol. 51. Academic Press. pp. 81–157. doi:10.1016/S0081-1947(08)60190-3. ISBN 978-0-12-607751-3.
- Koumoto, Kunihito; Mori, Takao (2013-07-20). Thermoelectric Nanomaterials: Materials Design and Applications. Springer Science & Business Media. ISBN 978-3-642-37537-8.
- Yanzhong, Pei; Heng, Wang; J., Snyder, G. (2012-12-04). "Band Engineering of Thermoelectric Materials". Advanced Materials. 24 (46): 6125–6135. Bibcode:2012AdM....24.6125P. doi:10.1002/adma.201202919. PMID 23074043. S2CID 205247155. Retrieved 2015-10-23.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Xing, Guangzong; Sun, Jifeng; Li, Yuwei; Fan, Xiaofeng; Zheng, Weitao; Singh, David J. (2017). "Electronic fitness function for screening semiconductors as thermoelectric materials". Physical Review Materials. 1 (6): 065405. arXiv:1708.04499. Bibcode:2017PhRvM...1f5405X. doi:10.1103/PhysRevMaterials.1.065405. S2CID 67790664.
- Bhandari, C. M. in Rowe 2018, pp. 55–65
- Cava, R. J. (1990). "Structural chemistry and the local charge picture of copper-oxide superconductors". Science. 247 (4943): 656–62. Bibcode:1990Sci...247..656C. doi:10.1126/science.247.4943.656. PMID 17771881. S2CID 32298034.
- Dresselhaus, M. S.; Chen, G.; Tang, M. Y.; Yang, R. G.; Lee, H.; Wang, D. Z.; Ren, Z. F.; Fleurial, J.-P.; Gogna, P. (2007). "New directions for low-dimensional thermoelectric materials" (PDF). Advanced Materials. 19 (8): 1043–1053. Bibcode:2007AdM....19.1043D. doi:10.1002/adma.200600527. S2CID 31648320.
- Duck Young Chung; Hogan, T.; Schindler, J.; Iordarridis, L.; Brazis, P.; Kannewurf, C.R.; Baoxing Chen; Uher, C.; Kanatzidis, M.G. (1997). "Complex bismuth chalcogenides as thermoelectrics". XVI ICT '97. Proceedings ICT'97. 16th International Conference on Thermoelectrics (Cat. No.97TH8291). p. 459. doi:10.1109/ICT.1997.667185. ISBN 978-0-7803-4057-2. S2CID 93624270.
- ^ Venkatasubramanian, Rama; Siivola, Edward; Colpitts, Thomas; O'Quinn, Brooks (2001). "Thin-film thermoelectric devices with high room-temperature figures of merit". Nature. 413 (6856): 597–602. Bibcode:2001Natur.413..597V. doi:10.1038/35098012. PMID 11595940. S2CID 4428804.
- Rowe 2018, Ch. 27.
- Heremans, J. P.; Jovovic, V.; Toberer, E. S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G. J. (2008). "Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States" (PDF). Science. 321 (5888): 554–7. Bibcode:2008Sci...321..554H. doi:10.1126/science.1159725. PMID 18653890. S2CID 10313813.
- Pei, Yanzhong; Lalonde, Aaron; Iwanaga, Shiho; Snyder, G. Jeffrey (2011). "High thermoelectric figure of merit in heavy hole dominated PbTe" (PDF). Energy & Environmental Science. 4 (6): 2085. doi:10.1039/C0EE00456A.
- Pei, Yanzhong; Shi, Xiaoya; Lalonde, Aaron; Wang, Heng; Chen, Lidong; Snyder, G. Jeffrey (2011). "Convergence of electronic bands for high performance bulk thermoelectrics" (PDF). Nature. 473 (7345): 66–9. Bibcode:2011Natur.473...66P. doi:10.1038/nature09996. PMID 21544143. S2CID 4313954.
- Quick, Darren (September 20, 2012). "World's most efficient thermoelectric material developed". Gizmag. Retrieved 16 December 2014.
- Biswas, K.; He, J.; Blum, I. D.; Wu, C. I.; Hogan, T. P.; Seidman, D. N.; Dravid, V. P.; Kanatzidis, M. G. (2012). "High-performance bulk thermoelectrics with all-scale hierarchical architectures". Nature. 489 (7416): 414–418. Bibcode:2012Natur.489..414B. doi:10.1038/nature11439. PMID 22996556. S2CID 4394616.
- Rowe 2018, 32–33.
- Gatti, C., Bertini, L., Blake, N. P. and Iversen, B. B. (2003). "Guest–Framework Interaction in Type I Inorganic Clathrates with Promising Thermoelectric Properties: On the Ionic versus Neutral Nature of the Alkaline-Earth Metal Guest A in A8Ga16Ge30 (A=Sr, Ba)". Chemistry: A European Journal. 9 (18): 4556–68. doi:10.1002/chem.200304837. PMID 14502642.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - Nolas, G. S., ed. (2014). The Physics and Chemistry of Inorganic Clathrates. Springer Series in Materials Science. Vol. 199. Springer Netherlands. Bibcode:2014pcic.book.....N. doi:10.1007/978-94-017-9127-4. ISBN 978-94-017-9126-7. S2CID 92675824.
- Martin, J., Nolas, G. S., Wang, H., Yang, J. (2007). "Thermoelectric properties of silicon-germanium type I clathrates". Journal of Applied Physics. 102 (10): 103719–103719–6. Bibcode:2007JAP...102j3719M. doi:10.1063/1.2817400. ISSN 0021-8979.
- Martin, J., Wang, H., Nolas, G. S. (2008). "Optimization of the thermoelectric properties of Ba8Ga16Ge30". Applied Physics Letters. 92 (22): 222110. Bibcode:2008ApPhL..92v2110M. doi:10.1063/1.2939438. ISSN 0003-6951.
- Beekman, M., Nolas, G. S. (2008). "Inorganic clathrate-II materials of group 14: synthetic routes and physical properties". Journal of Materials Chemistry. 18 (8): 842–851. doi:10.1039/B706808E. ISSN 0959-9428.
- Beekman, M., Nenghabi, E. N., Biswas, K., Myles, C. W., Baitinger, M., Grin, Y., Nolas, G. S. (2010). "Framework contraction in Na-stuffed Si(cF 136)". Inorganic Chemistry. 49 (12): 5338–5340. doi:10.1021/ic1005049. ISSN 0020-1669. PMID 20503981.
- Stefanoski, S., Malliakas, C. D., Kanatzidis, M. G., Nolas, G. S. (2012). "Synthesis and structural characterization of Na xSi 136 (0 < x ≤ 24) single crystals and low-temperature transport of polycrystalline specimens". Inorganic Chemistry. 51 (16): 8686–8692. doi:10.1021/ic202199t. ISSN 0020-1669. PMID 22873348.
- Rowe 2018, Ch. 32–33.
- Hirayama, Naomi; Iida, Tsutomu; Sakamoto, Mariko; Nishio, Keishi; Hamada, Noriaki (2019). "Substitutional and interstitial impurity p-type doping of thermoelectric Mg2Si: A theoretical study". Science and Technology of Advanced Materials. 20 (1): 160–172. Bibcode:2019STAdM..20..160H. doi:10.1080/14686996.2019.1580537. PMC 6419642. PMID 30891103.
- Khan, A.U.; Vlachos, N; Kyratsi, Th (2013). "High thermoelectric figure of merit of Mg2Si0.55−xSn0.4Ge0.05 materials doped with Bi and Sb". Scripta Materialia. 69 (8): 606–609. doi:10.1016/j.scriptamat.2013.07.008.
- Rowe 2018, Ch. 34.
- Nolas, G. S.; Slack, G. A.; Morelli, D. T.; Tritt, T. M.; Ehrlich, A. C. (1996). "The effect of rare-earth filling on the lattice thermal conductivity of skutterudites". Journal of Applied Physics. 79 (8): 4002. Bibcode:1996JAP....79.4002N. doi:10.1063/1.361828.
- Khan, Atta U.; Kobayashi, Kazuaki; Tang, Dai-Ming; Yamauchi, Yasuke; Hasegawa, Kotone; Mitome, Masanori; Xue, Yanming; Jiang, Baozhen; Tsuchiay, Koichi; Dmitri, Golberg; Mori, Takao (2017). "Nano-micro-porous skutterudites with 100% enhancement in ZT for high performance thermoelectricity". Nano Energy. 31: 152–159. Bibcode:2017NEne...31..152K. doi:10.1016/j.nanoen.2016.11.016.
- "Spacecraft 'Nuclear Batteries' Could Get a Boost from New Materials". JPL News. Jet Propulsion Laboratory. 13 October 2016.
- ^ Rowe 2018, Ch. 35.
- ^ Ohtaki, Michitaka (2011). "Recent aspects of oxide thermoelectric materials for power generation from mid-to-high temperature heat source". Journal of the Ceramic Society of Japan. 119 (11): 770–775. doi:10.2109/jcersj2.119.770. hdl:2324/25707.
- Matsuno, Jobu; Fujioka, Jun; Okuda, Tetsuji; Ueno, Kazunori; Mizokawa, Takashi; Katsufuji, Takuro (2018). "Strongly correlated oxides for energy harvesting". Science and Technology of Advanced Materials. 19 (1): 899–908. Bibcode:2018STAdM..19..899M. doi:10.1080/14686996.2018.1529524. PMC 6454405. PMID 31001365.
- Music, D.; Schneider, J.M. (2015). "Critical evaluation of the colossal Seebeck coefficient of nanostructured rutile MnO2". Journal of Physics: Condensed Matter. 27 (11): 115302. Bibcode:2015JPCM...27k5302M. doi:10.1088/0953-8984/27/11/115302. PMID 25730181. S2CID 25518753.
- Music, D.; Chen, Y.-T.; Bliem, P.; Geyer, R.W. (2015). "Amorphous-crystalline transition in thermoelectric NbO2". Journal of Physics D: Applied Physics. 48 (27): 275301. Bibcode:2015JPhD...48.5301M. doi:10.1088/0022-3727/48/27/275301. S2CID 120464503.
- Onozato, T.; Katase, T.; Yamamoto, A.; et al. (2016). "Optoelectronic properties of valence-state-controlled amorphous niobium oxide". Journal of Physics: Condensed Matter. 28 (25): 255001. Bibcode:2016JPCM...28y5001O. doi:10.1088/0953-8984/28/25/255001. PMID 27168317. S2CID 46879479.
- Lu, Xu; Morelli, Donald T.; Xia, Yi; Zhou, Fei; Ozolins, Vidvuds; Chi, Hang; Zhou, Xiaoyuan; Uher, Ctirad (March 2013). "High Performance Thermoelectricity in Earth-Abundant Compounds Based on Natural Mineral Tetrahedrites". Advanced Energy Materials. 3 (3): 342–348. Bibcode:2013AdEnM...3..342L. doi:10.1002/aenm.201200650. hdl:2027.42/97156. S2CID 51796822.
- ^ Khan, Atta Ullah; Orabi, Rabih Al Rahal Al; Pakdel, Amir; Vaney, Jean-Baptiste; Fontaine, Bruno; Gautier, Régis; Halet, Jean-François; Mitani, Seiji; Mori, Takao (11 April 2017). "Sb Doping of Metallic CuCr 2 S 4 as a Route to Highly Improved Thermoelectric Properties". Chemistry of Materials. 29 (7): 2988–2996. doi:10.1021/acs.chemmater.6b05344.
- ^ Long, Sebastian O. J.; Powell, Anthony V.; Vaqueiro, Paz; Hull, Stephen (23 January 2018). "High Thermoelectric Performance of Bornite through Control of the Cu(II) Content and Vacancy Concentration" (PDF). Chemistry of Materials. 30 (2): 456–464. doi:10.1021/acs.chemmater.7b04436.
- Lesnyak, Vladimir; Brescia, Rosaria; Messina, Gabriele C.; Manna, Liberato (29 July 2015). "Cu Vacancies Boost Cation Exchange Reactions in Copper Selenide Nanocrystals". Journal of the American Chemical Society. 137 (29): 9315–9323. Bibcode:2015JAChS.137.9315L. doi:10.1021/jacs.5b03868. PMC 4521286. PMID 26140622.
- Hodges, James M.; Kletetschka, Karel; Fenton, Julie L.; Read, Carlos G.; Schaak, Raymond E. (20 July 2015). "Sequential Anion and Cation Exchange Reactions for Complete Material Transformations of Nanoparticles with Morphological Retention". Angewandte Chemie International Edition. 54 (30): 8669–8672. doi:10.1002/anie.201504099. PMID 26110653.
- Lu, Xu; Morelli, Donald T.; Xia, Yi; Zhou, Fei; Ozolins, Vidvuds; Chi, Hang; Zhou, Xiaoyuan; Uher, Ctirad (2013). "High Performance Thermoelectricity in Earth-Abundant Compounds Based on Natural Mineral Tetrahedrites". Advanced Energy Materials. 3 (3): 342–348. Bibcode:2013AdEnM...3..342L. doi:10.1002/aenm.201200650. hdl:2027.42/97156. S2CID 51796822.
- ^ Huang, Lihong; Zhang, Qinyong; Yuan, Bo; Lai, Xiang; Yan, Xiao; Ren, Zhifeng (2016). "Recent progress in half-Heusler thermoelectric materials". Materials Research Bulletin. 76: 107–112. doi:10.1016/j.materresbull.2015.11.032.
- Yan, Xiao; Joshi, Giri; Liu, Weishu; Lan, Yucheng; Wang, Hui; Lee, Sangyeop; Simonson, J. W.; Poon, S. J.; Tritt, T. M.; Chen, Gang; Ren, Z. F. (2011). "Enhanced Thermoelectric Figure of Merit of p-Type Half-Heuslers". Nano Letters. 11 (2): 556–560. Bibcode:2011NanoL..11..556Y. doi:10.1021/nl104138t. PMID 21186782.
- Kimura, Yoshisato; Ueno, Hazuki; Mishima, Yoshinao (2009). "Thermoelectric Properties of Directionally Solidified Half-Heusler (M0.5,M0.5)NiSn (M, M = Hf, Zr, Ti) Alloys". Journal of Electronic Materials. 38 (7): 934–939. doi:10.1007/s11664-009-0710-x. S2CID 135974684.
- Tian, R.; Wan, C.; Hayashi, N.; Aoai, T. (March 2018). "Wearable and flexible thermoelectrics for energy harvesting". MRS Bulletin. 43 (3): 193–198. Bibcode:2018MRSBu..43..193T. doi:10.1557/mrs.2018.8. S2CID 139346335.
- Petsagkourakis, Ioannis; Tybrandt, Klas; Crispin, Xavier; Ohkubo, Isao; Satoh, Norifusa; Mori, Takao (2018). "Thermoelectric materials and applications for energy harvesting power generation". Science and Technology of Advanced Materials. 19 (1): 836–862. Bibcode:2018STAdM..19..836P. doi:10.1080/14686996.2018.1530938. PMC 6454408. PMID 31001364.
- Bannych, A.; Katz, S.; Barkay, Z.; Lachman, N. (Jun 2020). "Preserving Softness and Elastic Recovery in Silicone-Based Stretchable Electrodes Using Carbon Nanotubes". Polymers. 12 (6): 1345. doi:10.3390/polym12061345. PMC 7362250. PMID 32545911.
- Chung, D.D.L. (October 2018). "Thermoelectric polymer-matrix structural and nonstructural composite materials". Advance Industrial and Engineering Polymer Research. 1 (1): 61–65. doi:10.1016/j.aiepr.2018.04.001.
- Nandihalli, N.; Liu, C.; Mori, Takao (December 2020). "Polymer based thermoelectric nanocomposite materials and devices: Fabrication and characteristics". Nano Energy. 78: 105186. Bibcode:2020NEne...7805186N. doi:10.1016/j.nanoen.2020.105186.
- Okhay, O.; Tkach, A. (April 2021). "Impact of Graphene or Reduced Graphene Oxide on Performance of Thermoelectric Composites". C. 7 (2): 37. doi:10.3390/c7020037.
- Peng, J.; Witting, I.; Grayson, M.; Snyder, G.J.; Yan, X. (December 2019). "3D extruded composite thermoelectric threads for flexible energy harvesting". Nature Communications. 10 (1): 5590. Bibcode:2019NatCo..10.5590P. doi:10.1038/s41467-019-13461-2. PMC 6897922. PMID 31811127.
- ^ Zhan, Tianzhuo; Yamato, Ryo; Hashimoto, Shuichiro; Tomita, Motohiro; Oba, Shunsuke; Himeda, Yuya; Mesaki, Kohei; Takezawa, Hiroki; Yokogawa, Ryo; Xu, Yibin; Matsukawa, Takashi; Ogura, Atsushi; Kamakura, Yoshinari; Watanabe, Takanobu (2018). "Miniaturized planar Si-nanowire micro-thermoelectric generator using exuded thermal field for power generation". Science and Technology of Advanced Materials. 19 (1): 443–453. Bibcode:2018STAdM..19..443Z. doi:10.1080/14686996.2018.1460177. PMC 5974757. PMID 29868148.
- ^ Nakamura, Yoshiaki (2018). "Nanostructure design for drastic reduction of thermal conductivity while preserving high electrical conductivity". Science and Technology of Advanced Materials. 19 (1): 31–43. Bibcode:2018STAdM..19...31N. doi:10.1080/14686996.2017.1413918. PMC 5769778. PMID 29371907.
- Dismukes, J.P.; Ekstrom, E.; Beers, D.S.; Steigmeier, E.F.; Kudman, I. (1964). "Thermal and electrical properties of heavily doped Ge-Si alloys up to 1300 °K". Journal of Applied. 35 (10): 2899. Bibcode:1964JAP....35.2899D. doi:10.1063/1.1713126. ISSN 0021-8979.
- ^ Kandemir, Ali; Ozden, Ayberk; Cagin, Tahir; Sevik, Cem (2017). "Thermal conductivity engineering of bulk and one-dimensional Si-Ge nanoarchitectures". Science and Technology of Advanced Materials. 18 (1): 187–196. Bibcode:2017STAdM..18..187K. doi:10.1080/14686996.2017.1288065. PMC 5404179. PMID 28469733.
- "Improved thermoelectric materials may give a push to Moore's law". KurzweilAI. September 2, 2013.
- Voneshen, D. J.; Refson, K.; Borissenko, E.; Krisch, M.; Bosak, A.; Piovano, A.; Cemal, E.; Enderle, M.; Gutmann, M. J.; Hoesch, M.; Roger, M.; Gannon, L.; Boothroyd, A. T.; Uthayakumar, S.; Porter, D. G.; Goff, J. P. (2013). "Suppression of thermal conductivity by rattling modes in thermoelectric sodium cobaltate" (PDF). Nature Materials. 12 (11): 1028–1032. Bibcode:2013NatMa..12.1028V. doi:10.1038/nmat3739. PMID 23975057.
- Nolas, G.S.; Goldsmid, H.J. (2002). "The figure of merit in amorphous thermoelectrics". Physica Status Solidi A. 194 (1): 271–276. Bibcode:2002PSSAR.194..271N. doi:10.1002/1521-396X(200211)194:1<271::AID-PSSA271>3.0.CO;2-T.
- Goncalves, A.P.; Lopes, E.B.; Rouleau, O.; Godart, C. (2010). "Conducting glasses as new potential thermoelectric materials: the Cu-Ge-Te case". Journal of Materials Chemistry. 20 (8): 1516–1521. doi:10.1039/B908579C. S2CID 56230957.
- Music, D.; Geyer, R.W.; Hans, M. (2016). "High-throughput exploration of thermoelectric and mechanical properties of amorphous NbO2 with transition metal additions". Journal of Applied Physics. 120 (4): 045104. Bibcode:2016JAP...120d5104M. doi:10.1063/1.4959608.
- Fujimoto, Y.; Uenuma, M.; Ishikawa, Y.; Uraoka, Y. (2015). "Analysis of thermoelectric properties of amorphous InGaZnO thin film by controlling carrier concentration". AIP Advances. 5 (9): 097209. Bibcode:2015AIPA....5i7209F. doi:10.1063/1.4931951.
- Zhou, Y.; Tan, Q.; Zhu, J.; Li, S.; Liu, C.; Lei, Y.; Li, L. (2015). "Thermoelectric properties of amorphous Zr-Ni-Sn thin films deposited by magnetron sputtering". Journal of Electronic Materials. 44 (6): 1957–1962. Bibcode:2015JEMat..44.1957Z. doi:10.1007/s11664-014-3610-7.
- Takiguchi, H.; Yoshikawa, Z.; Miyazaki, H.; Okamoto, Y.; Morimoto, J. (2010). "The Role of Au in the Thermoelectric Properties of Amorphous Ge/Au and Si/Au Thin Films". Journal of Electronic Materials. 39 (9): 1627–1633. Bibcode:2010JEMat..39.1627T. doi:10.1007/s11664-010-1267-4. S2CID 54579660.
- Ramesh, K. V; Sastry, D. L (2007). "DC electrical conductivity, thermoelectric power measurements of TiO2-substituted lead vanadate glasses". Physica B. 387 (1–2): 45–51. Bibcode:2007PhyB..387...45R. doi:10.1016/j.physb.2006.03.026.
- Rowe 2018, Ch. 38.
- ^ Harman, T. C.; Taylor, PJ; Walsh, MP; Laforge, BE (2002). "Quantum dot superlattice thermoelectric materials and devices" (PDF). Science. 297 (5590): 2229–32. Bibcode:2002Sci...297.2229H. doi:10.1126/science.1072886. PMID 12351781. S2CID 18657048.
- Rowe 2018, Ch. 40.
- Rowe 2018, Ch. 41.
- ^ Anno, Yuki; Imakita, Yuki; Takei, Kuniharu; Akita, Seiji; Arie, Takayuki (2017). "Enhancement of graphene thermoelectric performance through defect engineering". 2D Materials. 4 (2): 025019. Bibcode:2017TDM.....4b5019A. doi:10.1088/2053-1583/aa57fc.
- ^ Mu, X.; Wu, X.; Zhang, T.; Go, D. B.; Luo, T. (2014). "Thermal transport in graphene oxide—from ballistic extreme to amorphous limit". Scientific Reports. 4: 3909. Bibcode:2014NatSR...4.3909M. doi:10.1038/srep03909. PMC 3904152. PMID 24468660.
- Cataldi, Pietro; Cassinelli, Marco; Heredia Guerrero, Jose; Guzman-Puyol, Susana; Naderizadeh, Sara; Athanassiou, Athanassia; Caironi, Mario (2020). "Green Biocomposites for Thermoelectric Wearable Applications". Advanced Functional Materials. 30 (3): 1907301. doi:10.1002/adfm.201907301. S2CID 208760903.
- Anno, Yuki; Takei, Kuniharu; Akita, Seiji; Arie, Takayuki (2014). "Artificially controlled synthesis of graphene intramolecular heterojunctions for phonon engineering". Physica Status Solidi RRL. 8 (8): 692–697. Bibcode:2014PSSRR...8..692A. doi:10.1002/pssr.201409210. S2CID 97144447.
- Chen, Shanshan; Li, Qiongyu; Zhang, Qimin; Qu, Yan; Ji, Hengxing; Ruoff, Rodney S; Cai, Weiwei (2012). "Thermal conductivity measurements of suspended graphene with and without wrinkles by micro-Raman mapping". Nanotechnology. 23 (36): 365701. Bibcode:2012Nanot..23J5701C. doi:10.1088/0957-4484/23/36/365701. PMID 22910228. S2CID 15154844.
- Rowe 2018, Ch. 16, 39.
- Rowe 2018, Ch. 39.
- Rowe 2018, Ch. 49.
- Minnich, A. J.; Dresselhaus, M. S.; Ren, Z. F.; Chen, G. (2009). "Bulk nanostructured thermoelectric materials: current research and future prospects". Energy & Environmental Science. 2 (5): 466. doi:10.1039/b822664b. S2CID 14722249.
- Biswas, Kanishka; He, Jiaqing; Zhang, Qichun; Wang, Guoyu; Uher, Ctirad; Dravid, Vinayak P.; Kanatzidis, Mercouri G. (2011). "Strained endotaxial nanostructure with high thermoelectric figure of merit". Nature Chemistry. 3 (2): 160–6. Bibcode:2011NatCh...3..160B. doi:10.1038/nchem.955. PMID 21258390.
- Zhao, Li-Dong; Lo, Shih-Han; Zhang, Yongsheng; Sun, Hui; Tan, Gangjian; Uher, Ctirad; Wolverton, C.; Dravid, Vinayak P.; Kanatzidis, Mercouri G. (2014). "Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals". Nature. 508 (7496): 373–7. Bibcode:2014Natur.508..373Z. doi:10.1038/nature13184. PMID 24740068. S2CID 205238132.
- Zhang, H.; Talapin, D. V. (2014). "Thermoelectric Tin Selenide: The Beauty of Simplicity". Angew. Chem. Int. Ed. 53 (35): 9126–9127. doi:10.1002/anie.201405683. PMID 25044424.
- ^ Zhao, L-D.; Lo, S-H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.; Kanatzidis, M. (2014). "Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals". Nature. 508 (7496): 373–377. Bibcode:2014Natur.508..373Z. doi:10.1038/nature13184. PMID 24740068. S2CID 205238132.
- Zhao, Li-Dong; Lo, Shih-Han; Zhang, Yongsheng; Sun, Hui; Tan, Gangjian; Uher, Ctirad; Wolverton, C.; Dravid, Vinayak P.; Kanatzidis, Mercouri G. (2014). "Ultralow thermal conductivity and high thermoelectric figure of merit in Sn Se crystals". Nature. 508 (7496): 373–377. Bibcode:2014Natur.508..373Z. doi:10.1038/nature13184. PMID 24740068. S2CID 205238132.
- Bernardes-Silva, Ana Cláudia; Mesquita, A.F.; Neto, E. de Moura; Porto, A.O.; Ardisson, J.D.; Lima, G.M. de; Lameiras, F.S. (2005). "XRD and Sn Mossbauer spectroscopy characterization of SnSe obtained from a simple chemical route". Materials Research Bulletin. 40 (9): 1497–1505. doi:10.1016/j.materresbull.2005.04.021.
- Chen, C-L.; Wang, H.; Chen, Y-Y.; Daya, T.; Snyder, G. J. (2014). "Thermoelectric properties of p-type polycrystalline SnSe doped with Ag" (PDF). J. Mater. Chem. A. 2 (29): 11171. doi:10.1039/c4ta01643b.
- Irving, Michael (2021-08-03). "Extremely efficient thermoelectric material recycles waste heat". New Atlas. Retrieved 2021-08-03.
- Anderson, P. W. (1958-03-01). "Absence of Diffusion in Certain Random Lattices". Physical Review. 109 (5): 1492–1505. Bibcode:1958PhRv..109.1492A. doi:10.1103/PhysRev.109.1492. ISSN 0031-899X.
- Izawa, Tetsumi; Takashima, Kengo; Yamamoto, Takahiro (November 2016). "Edge-disorder-induced optimization of thermoelectric performance of finite-length graphene nanoribbons". Surface and Interface Analysis. 48 (11): 1210–1213. doi:10.1002/sia.6095. ISSN 0142-2421. S2CID 99840055.
- Adessi, Ch.; Thebaud, S.; Bouzerar, R.; Bouzerar, G. (2017-06-15). "First Principle Investigation on Thermoelectric Properties of Transition Metal Dichalcogenides: Beyond the Rigid Band Model". The Journal of Physical Chemistry C. 121 (23): 12577–12584. doi:10.1021/acs.jpcc.7b02570. ISSN 1932-7447.
- Tian, Zhiting (2019-04-23). "Anderson Localization for Better Thermoelectrics?". ACS Nano. 13 (4): 3750–3753. doi:10.1021/acsnano.9b02399. ISSN 1936-0851. PMID 30973217. S2CID 108295349.
- Lee, Min Ho; Yun, Jae Hyun; Kim, Gareoung; Lee, Ji Eun; Park, Su-Dong; Reith, Heiko; Schierning, Gabi; Nielsch, Konelius; Ko, Wonhee; Li, An-Ping; Rhyee, Jong-Soo (2019-04-23). "Synergetic Enhancement of Thermoelectric Performance by Selective Charge Anderson Localization–Delocalization Transition in n-Type Bi-Doped PbTe/Ag 2 Te Nanocomposite". ACS Nano. 13 (4): 3806–3815. doi:10.1021/acsnano.8b08579. ISSN 1936-0851. PMID 30735348. S2CID 73433892.
- Yazdani, Sajad; Pettes, Michael Thompson (2018-10-26). "Nanoscale self-assembly of thermoelectric materials: a review of chemistry-based approaches". Nanotechnology. 29 (43): 432001. Bibcode:2018Nanot..29Q2001Y. doi:10.1088/1361-6528/aad673. ISSN 0957-4484. PMID 30052199.
- He, Jian; Tritt, Terry M. (2017-09-29). "Advances in thermoelectric materials research: Looking back and moving forward". Science. 357 (6358): eaak9997. doi:10.1126/science.aak9997. ISSN 0036-8075. PMID 28963228.
- Wang, Liming; Zhang, Zimeng; Geng, Linxiao; Yuan, Tianyu; Liu, Yuchen; Guo, Juchen; Fang, Lei; Qiu, Jingjing; Wang, Shiren (2018). "Solution-printable fullerene/TiS2 organic/inorganic hybrids for high-performance flexible n-type thermoelectrics". Energy & Environmental Science. 11 (5): 1307–1317. doi:10.1039/c7ee03617e.
- U.S. Department of Energy (2015). "Quadrennial Technology Review 2015, Chapter 6: Innovating Clean Energy Technologies in Advanced Manufacturing" (PDF). Retrieved 2020-11-17.
- Kim, Fredrick; Kwon, Beomjin; Eom, Youngho; Lee, Ji Eun; Park, Sangmin; Jo, Seungki; Park, Sung Hoon; Kim, Bong-Seo; Im, Hye Jin (2018). "3D printing of shape-conformable thermoelectric materials using all-inorganic Bi2Te3-based inks". Nature Energy. 3 (4): 301–309. Bibcode:2018NatEn...3..301K. doi:10.1038/s41560-017-0071-2. S2CID 139489568.
- Orrill, Michael; LeBlanc, Saniya (2017-01-15). "Printed thermoelectric materials and devices: Fabrication techniques, advantages, and challenges: REVIEW". Journal of Applied Polymer Science. 134 (3). doi:10.1002/app.44256.
- ^ Zhang, Haidong; Hobbis, Dean; Nolas, George S.; LeBlanc, Saniya (2018-12-14). "Laser additive manufacturing of powdered bismuth telluride". Journal of Materials Research. 33 (23): 4031–4039. Bibcode:2018JMatR..33.4031Z. doi:10.1557/jmr.2018.390. ISSN 0884-2914. S2CID 139907097.
- Kim, Fredrick; Kwon, Beomjin; Eom, Youngho; Lee, Ji Eun; Park, Sangmin; Jo, Seungki; Park, Sung Hoon; Kim, Bong-Seo; Im, Hye Jin; Lee, Min Ho; Min, Tae Sik (April 2018). "3D printing of shape-conformable thermoelectric materials using all-inorganic Bi 2 Te 3 -based inks". Nature Energy. 3 (4): 301–309. Bibcode:2018NatEn...3..301K. doi:10.1038/s41560-017-0071-2. ISSN 2058-7546. S2CID 139489568.
- Ren, Zhifeng; Lan, Yucheng; Zhang, Qinyong (2017-11-06), "Introduction to Thermoelectric Materials, Contacts, Devices, and Systems", Advanced Thermoelectrics, Boca Raton, FL : CRC Press, Taylor & Francis Group, | Series: Series in materials science and engineering: CRC Press, pp. 3–8, doi:10.1201/9781315153766-1, ISBN 978-1-315-15376-6, retrieved 2023-05-11
{{citation}}: CS1 maint: location (link) - Al-Merbati, A. S.; Yilbas, B. S.; Sahin, A. Z. (2013-01-10). "Thermodynamics and thermal stress analysis of thermoelectric power generator: Influence of pin geometry on device performance". Applied Thermal Engineering. 50 (1): 683–692. Bibcode:2013AppTE..50..683A. doi:10.1016/j.applthermaleng.2012.07.021. ISSN 1359-4311.
- Erturun, Ugur; Erermis, Kaan; Mossi, Karla (December 2014). "Effect of various leg geometries on thermo-mechanical and power generation performance of thermoelectric devices". Applied Thermal Engineering. 73 (1): 128–141. Bibcode:2014AppTE..73..128E. doi:10.1016/j.applthermaleng.2014.07.027.
- Suhir, E.; Shakouri, A. (November 2012). "Assembly Bonded at the Ends: Could Thinner and Longer Legs Result in a Lower Thermal Stress in a Thermoelectric Module Design?". Journal of Applied Mechanics. 79 (6). American Society of Mechanical Engineers: 061010. Bibcode:2012JAM....79f1010S. doi:10.1115/1.4006597. Archived from the original on February 10, 2020. Retrieved 2023-05-14.
- Suhir, E.; Shakouri, A. (2013-01-22). "Predicted Thermal Stress in a Multileg Thermoelectric Module (TEM) Design". Journal of Applied Mechanics. 80 (2): 021012. Bibcode:2013JAM....80b1012S. doi:10.1115/1.4007524. ISSN 0021-8936.
- Ziabari, Amirkoushyar; Suhir, Ephraim; Shakouri, Ali (May 2014). "Minimizing thermally induced interfacial shearing stress in a thermoelectric module with low fractional area coverage". Microelectronics Journal. 45 (5): 547–553. doi:10.1016/j.mejo.2013.12.004. S2CID 13009734.
- Kishore, Ravi Anant; Sanghadasa, Mohan; Priya, Shashank (2017-12-01). "Optimization of segmented thermoelectric generator using Taguchi and ANOVA techniques". Scientific Reports. 7 (1): 16746. Bibcode:2017NatSR...716746K. doi:10.1038/s41598-017-16372-8. ISSN 2045-2322. PMC 5711871. PMID 29196715.
- Tachibana, Makoto; Fang, Jianjun (2012-01-01). "An Estimation of Thermal Stress of Thermoelectric Devices in the Temperature Cycling Test". Procedia Engineering. 27: 177–185. doi:10.1016/j.proeng.2011.12.441. ISSN 1877-7058.
- Clin, Th.; Turenne, S.; Vasilevskiy, D.; Masut, R. A. (2009-07-01). "Numerical Simulation of the Thermomechanical Behavior of Extruded Bismuth Telluride Alloy Module". Journal of Electronic Materials. 38 (7): 994–1001. Bibcode:2009JEMat..38..994C. doi:10.1007/s11664-009-0756-9. ISSN 1543-186X. S2CID 136972257.
- Turenne, S.; Clin, Th.; Vasilevskiy, D.; Masut, R. A. (2010-09-01). "Finite Element Thermomechanical Modeling of Large Area Thermoelectric Generators based on Bismuth Telluride Alloys". Journal of Electronic Materials. 39 (9): 1926–1933. Bibcode:2010JEMat..39.1926T. doi:10.1007/s11664-009-1049-z. ISSN 1543-186X. S2CID 95338608.
- Zheng, Yun; Tan, Xian Yi; Wan, Xiaojuan; Cheng, Xin; Liu, Zhihong; Yan, Qingyu (2020-03-23). "Thermal Stability and Mechanical Response of Bi 2 Te 3 -Based Materials for Thermoelectric Applications". ACS Applied Energy Materials. 3 (3): 2078–2089. doi:10.1021/acsaem.9b02093. ISSN 2574-0962. S2CID 210263333.
- Pelletier, R.; Turenne, S.; Moreau, A.; Vasilevskiy, D.; Masut, R.A. (June 2007). "Evolution of mechanical stresses in extruded (Bi1−xSbx)2(Te1−ySey)3 thermoelectric alloys subjected to thermal shocks present in module fabrication processes". 2007 26th International Conference on Thermoelectrics. pp. 49–54. doi:10.1109/ICT.2007.4569421. ISBN 978-1-4244-2262-3. S2CID 24892404.
- Sakamoto, Tatsuya; Iida, Tsutomu; Ohno, Yota; Ishikawa, Masashi; Kogo, Yasuo; Hirayama, Naomi; Arai, Koya; Nakamura, Takashi; Nishio, Keishi; Takanashi, Yoshifumi (2014-06-01). "Stress Analysis and Output Power Measurement of an n-Mg2Si Thermoelectric Power Generator with an Unconventional Structure". Journal of Electronic Materials. 43 (6): 1620–1629. doi:10.1007/s11664-013-2814-6. ISSN 1543-186X. S2CID 98084052.
- Chen, Si; Wang, Zhizhe; Zhou, Bin; En, Yunfei; Huang, Yun; Yao, Bin (December 2018). "Cracking failure of Cu pillar bump caused by electromigration and stress concentration under thermo-electric coupling loads". 2018 IEEE 20th Electronics Packaging Technology Conference (EPTC). Singapore, Singapore: IEEE. pp. 316–320. doi:10.1109/EPTC.2018.8654276. ISBN 978-1-5386-7668-4. S2CID 67875385.
- ^ Malki, Muath M. Al; Snyder, Jeffrey G.; Dunand, David C. (2023-04-26). "Mechanical behaviour of thermoelectric materials – a perspective". International Materials Reviews. 68 (8): 1050–1074. Bibcode:2023IMRv...68.1050A. doi:10.1080/09506608.2023.2193785. ISSN 0950-6608. S2CID 258396021.
- Liang, Qi; Yang, Dongwang; Xia, Fanjie; Bai, Hui; Peng, Haoyang; Yu, Ruohan; Yan, Yonggao; He, Danqi; Cao, Shaowen; Van Tendeloo, Gustaaf; Li, Guodong; Zhang, Qingjie; Tang, Xinfeng; Wu, Jinsong (December 2021). "Phase-Transformation-Induced Giant Deformation in Thermoelectric Ag 2 Se Semiconductor". Advanced Functional Materials. 31 (50): 2106938. doi:10.1002/adfm.202106938. ISSN 1616-301X. S2CID 239092658.
- Qi, Dekui; Tang, Xinfeng; Li, Han; Yan, Yonggao; Zhang, Qingjie (2010-08-01). "Improved Thermoelectric Performance and Mechanical Properties of Nanostructured Melt-Spun β-Zn4Sb3". Journal of Electronic Materials. 39 (8): 1159–1165. Bibcode:2010JEMat..39.1159Q. doi:10.1007/s11664-010-1288-z. ISSN 1543-186X. S2CID 94645998.
- ^ Champier, Daniel (2017). "Thermoelectric generators: A review of applications". Energy Conversion and Management. 140: 162–181. Bibcode:2017ECM...140..167C. doi:10.1016/j.enconman.2017.02.070.
- Tritt, Terry M.; Subramanian, M. A. (2011). "Thermoelectric Materials, Phenomena, and Applications: A Bird's Eye View". MRS Bulletin. 31 (3): 188–198. Bibcode:2011MRSBu..31..188T. doi:10.1557/mrs2006.44.
- Hinterleitner, B.; Knapp, I.; Poneder, M.; Shi, Yongpeng; Müller, H.; Eguchi, G.; Eisenmenger-Sittner, C.; Stöger-Pollach, M.; Kakefuda, Y.; Kawamoto, N.; Guo, Q. (2019-12-05). "Thermoelectric performance of a metastable thin-film Heusler alloy". Nature. 576 (7785): 85–90. Bibcode:2019Natur.576...85H. doi:10.1038/s41586-019-1751-9. ISSN 0028-0836. PMID 31723266. S2CID 207988713.
- "New material breaks world record for turning heat into electricity".
- ^ Fernández-Yáñez, P. (2021). "Thermal management of thermoelectric generators for waste energy recovery". Applied Thermal Engineering. 196 (published 2021-09-01): 117291. Bibcode:2021AppTE.19617291F. doi:10.1016/j.applthermaleng.2021.117291.
- Labudovic, M.; Li, J. (2004). "Modeling of TE cooling of pump lasers". IEEE Transactions on Components and Packaging Technologies. 27 (4): 724–730. doi:10.1109/TCAPT.2004.838874. S2CID 32351101.
- ^ Yang, J. (2005). "Potential applications of thermoelectric waste heat recovery in the automotive industry". ICT 2005. 24th International Conference on Thermoelectrics, 2005. p. 170. doi:10.1109/ICT.2005.1519911. ISBN 978-0-7803-9552-7. S2CID 19711673.
- Fairbanks, J. (2006-08-24) Thermoelectric Developments for Vehicular Applications, U.S. Department of Energy: Energy Efficiency and Renewable Energy.
- Goldsmid, H.J.; Giutronich, J.E.; Kaila, M.M. (1980). "Thermoelectrics: Direct Solar Thermal Energy Conversion" (PDF). Solar Energy. 24 (5): 435–440. Bibcode:1980SoEn...24..435G. doi:10.1016/0038-092X(80)90311-4.
Bibliography
- Rowe, D.M. (2018) . Thermoelectrics Handbook: Macro to Nano. CRC Press. ISBN 978-1-4200-3890-3.
External links
- TE Modules Application Tips and Hints Archived 2010-03-23 at the Wayback Machine
- The Seebeck Coefficient
- Materials for Thermoelectric Devices (4th chapter of Martin Wagner dissertation)
- New material breaks world record for turning heat into electricity
 , given by
, given by
 , defined as
, defined as 
 where the maximum device efficiency is approximately given by
where the maximum device efficiency is approximately given by  where
where  is the fixed temperature at the hot junction,
is the fixed temperature at the hot junction,  is the fixed temperature at the surface being cooled, and
is the fixed temperature at the surface being cooled, and  is the mean of
is the mean of  is then calculated from the efficiency of both legs and the electrical and thermal losses from the interconnects and surroundings.
is then calculated from the efficiency of both legs and the electrical and thermal losses from the interconnects and surroundings.
 where
where  is the electrical resistivity, and the properties are averaged over the temperature range; the subscripts n and p denote properties related to the n- and p-type semiconducting thermoelectric materials, respectively. Only when n and p elements have the same and temperature independent properties (
is the electrical resistivity, and the properties are averaged over the temperature range; the subscripts n and p denote properties related to the n- and p-type semiconducting thermoelectric materials, respectively. Only when n and p elements have the same and temperature independent properties ( ) does
) does  .
.
 , the first factor in
, the first factor in  where S is the
where S is the  .
.
 of a material is given by the material's quality factor
of a material is given by the material's quality factor

 is the Boltzmann constant,
is the Boltzmann constant,  is the reduced Planck constant,
is the reduced Planck constant,  is the number of degenerated valleys for the band,
is the number of degenerated valleys for the band,  is the average longitudinal elastic moduli,
is the average longitudinal elastic moduli,  is the inertial effective mass,
is the inertial effective mass,  is the deformation potential coefficient,
is the deformation potential coefficient,  is the lattice thermal conduction, and
is the lattice thermal conduction, and  is temperature. The figure of merit,
is temperature. The figure of merit,  is useful because it allows for an intrinsic comparison of possible efficiency between different materials. This relation shows that improving the electronic component
is useful because it allows for an intrinsic comparison of possible efficiency between different materials. This relation shows that improving the electronic component  , which primarily affects the Seebeck coefficient, will increase the quality factor of a material. A large density of states can be created due to a large number of conducting bands (
, which primarily affects the Seebeck coefficient, will increase the quality factor of a material. A large density of states can be created due to a large number of conducting bands ( ). For isotropic materials
). For isotropic materials  . Therefore, it is desirable for thermoelectric materials to have high valley degeneracy in a very sharp band structure. Other complex features of the electronic structure are important. These can be partially quantified using an electronic fitness function.
. Therefore, it is desirable for thermoelectric materials to have high valley degeneracy in a very sharp band structure. Other complex features of the electronic structure are important. These can be partially quantified using an electronic fitness function.
 , where L, α, ΔT and h are module thickness, Coefficients of Thermal Expansion(CTE), temperature difference and leg height, respectively.
, where L, α, ΔT and h are module thickness, Coefficients of Thermal Expansion(CTE), temperature difference and leg height, respectively.
 -based materials and they proposed that their fatigue behavior can be reduced via boosting the fracture toughness by introducing pores, microcracks or inclusion with the inextricable trade-off with fracture strength.
-based materials and they proposed that their fatigue behavior can be reduced via boosting the fracture toughness by introducing pores, microcracks or inclusion with the inextricable trade-off with fracture strength.
 -based structure was investigated that could utilize thermoelectric legs at an angle with elecftrical interconnects and substrates. Maximum tensile strength stresses were calculated and compared to the ultimate tensile strength of different materials. This approach might be misleading for brittle materials (such as ceramics) as they do not possess a defined tensile strength.
-based structure was investigated that could utilize thermoelectric legs at an angle with elecftrical interconnects and substrates. Maximum tensile strength stresses were calculated and compared to the ultimate tensile strength of different materials. This approach might be misleading for brittle materials (such as ceramics) as they do not possess a defined tensile strength.
 transforms to a body centered cubic phase. Liang et al. showed that a crack was observed when heating through 407 K through this phase transformation.
transforms to a body centered cubic phase. Liang et al. showed that a crack was observed when heating through 407 K through this phase transformation.