The two-rays ground-reflection model is a multipath radio propagation model which predicts the path losses between a transmitting antenna and a receiving antenna when they are in line of sight (LOS). Generally, the two antenna each have different height. The received signal having two components, the LOS component and the reflection component formed predominantly by a single ground reflected wave.
- The 2-ray ground reflection model is a simplified propagation model used to estimate the path loss between a transmitter and a receiver in wireless communication systems, in order to estimate the actual communication paths used. It assumes that the signal propagates through two paths:
1) Direct Path: A direct line-of-sight path between the transmitter and receiver antennas. 2) Reflected path: The path through which the signal reflects off the ground before reaching the receiver.

Mathematical derivation
From the figure the received line of sight component may be written as
and the ground reflected component may be written as
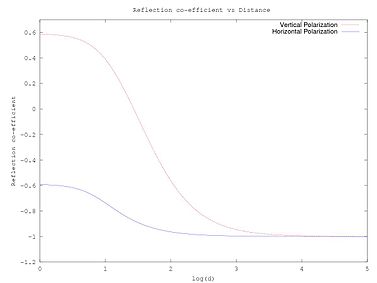
where is the transmitted signal, is the length of the direct line-of-sight (LOS) ray, is the length of the ground-reflected ray, is the combined antenna gain along the LOS path, is the combined antenna gain along the ground-reflected path, is the wavelength of the transmission (, where is the speed of light and is the transmission frequency), is ground reflection coefficient and is the delay spread of the model which equals . The ground reflection coefficient is
where or depending if the signal is horizontal or vertical polarized, respectively. is computed as follows.
The constant is the relative permittivity of the ground (or generally speaking, the material where the signal is being reflected), is the angle between the ground and the reflected ray as shown in the figure above.
From the geometry of the figure, yields:
and
- ,
Therefore, the path-length difference between them is
and the phase difference between the waves is
The power of the signal received is
where denotes average (over time) value.
Approximation
If the signal is narrow band relative to the inverse delay spread , so that , the power equation may be simplified to
where is the transmitted power.
When distance between the antennas is very large relative to the height of the antenna we may expand ,
using the Taylor series of :
and taking the first two terms only,
The phase difference can then be approximated as
When is large, ,
and hence
Expanding using Taylor series
and retaining only the first two terms
it follows that
so that
and path loss is
which is accurate in the far field region, i.e. when (angles are measured here in radians, not degrees) or, equivalently,
and where the combined antenna gain is the product of the transmit and receive antenna gains, . This formula was first obtained by B.A. Vvedenskij.
Note that the power decreases with as the inverse fourth power of the distance in the far field, which is explained by the destructive combination of the direct and reflected paths, which are roughly of the same in magnitude and are 180 degrees different in phase. is called "effective isotropic radiated power" (EIRP), which is the transmit power required to produce the same received power if the transmit antenna were isotropic.
In logarithmic units
In logarithmic units :
Path loss :
Power vs. distance characteristics
When the distance between antennas is less than the transmitting antenna height, two waves are added constructively to yield bigger power. As distance increases, these waves add up constructively and destructively, giving regions of up-fade and down-fade. As the distance increases beyond the critical distance or first Fresnel zone, the power drops proportionally to an inverse of fourth power of . An approximation to critical distance may be obtained by setting Δφ to π as the critical distance to a local maximum.
An extension to large antenna heights
The above approximations are valid provided that , which may be not the case in many scenarios, e.g. when antenna heights are not much smaller compared to the distance, or when the ground cannot be modelled as an ideal plane . In this case, one cannot use and more refined analysis is required, see e.g.
Propagation modeling for high-altitude platforms, UAVs, drones, etc.
The above large antenna height extension can be used for modeling a ground-to-the-air propagation channel as in the case of an airborne communication node, e.g. an UAV, drone, high-altitude platform. When the airborne node altitude is medium to high, the relationship does not hold anymore, the clearance angle is not small and, consequently, does not hold either. This has a profound impact on the propagation path loss and typical fading depth and the fading margin required for the reliable communication (low outage probability).
As a case of log distance path loss model
The standard expression of Log distance path loss model in is
where is the large-scale (log-normal) fading, is a reference distance at which the path loss is , is the path loss exponent; typically . This model is particularly well-suited for measurements, whereby and are determined experimentally; is selected for convenience of measurements and to have clear line-of-sight. This model is also a leading candidate for 5G and 6G systems and is also used for indoor communications, see e.g. and references therein.
The path loss of the 2-ray model is formally a special case with :
where , , and
- ,
which is valid the far field, = the critical distance.
As a case of multi-slope model
The 2-ray ground reflected model may be thought as a case of multi-slope model with break point at critical distance with slope 20 dB/decade before critical distance and slope of 40 dB/decade after the critical distance. Using the free-space and two-ray model above, the propagation path loss can be expressed as
where and are the free-space and 2-ray path losses; is a minimum path loss (at smallest distance), usually in practice; dB or so. Note that and also follow from the law of energy conservation (since the Rx power cannot exceed the Tx power) so that both and break down when is small enough. This should be kept in mind when using these approximations at small distances (ignoring this limitation sometimes produces absurd results).
See also
- Path loss
- Radio propagation model
- Free-space path loss
- Friis transmission equation
- ITU-R P.525
- Link budget
- Ray tracing (physics)
- Reflection (physics)
- Specular reflection
- Six-rays model
- Ten-rays model
References
- ^ Jakes, W.C. (1974). Microwave Mobile Communications. New York: IEEE Press.
- ^ Rappaport, Theodore S. (2002). Wireless Communications: Principles and Practice (2. ed.). Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0130422323.
- Vvedenskij, B.A. (December 1928). "On Radio Communications via Ultra-Short Waves". Theoretical and Experimental Electrical Engineering (12): 447–451.
- ^ Loyka, Sergey; Kouki, Ammar (October 2001). "Using Two Ray Multipath Model for Microwave Link Budget Analysis". IEEE Antennas and Propagation Magazine. 43 (5): 31–36. Bibcode:2001IAPM...43...31L. doi:10.1109/74.979365.
- ^ Loyka, Sergey; Kouki, Ammar; Gagnon, Francois (Oct 2001). Fading Prediction on Microwave Links for Airborne Communications. IEEE Vehicular Technology Conference. Atlantic City, USA.
- Rappaport, T. S.; et al. (Dec 2017). "Overview of millimeter wave communications for fifth-generation (5G) wireless networks — with a focus on propagation models". IEEE Transactions on Antennas and Propagation. 65 (12): 6213–6230. arXiv:1708.02557. Bibcode:2017ITAP...65.6213R. doi:10.1109/TAP.2017.2734243. S2CID 21557844.
- Rappaport, T. S.; et al. (June 2019). "Wireless Communications and Applications Above 100 GHz: Opportunities and Challenges for 6G and Beyond". IEEE Access. 7: 78729–78757. Bibcode:2019IEEEA...778729R. doi:10.1109/ACCESS.2019.2921522. S2CID 195740426.
- "ITU model for indoor attenuation", Misplaced Pages, 2021-03-14, retrieved 2022-01-24; see also
Further reading
- S. Salous, Radio Propagation Measurement and Channel Modelling, Wiley, 2013.
- J.S. Seybold, Introduction to RF propagation, Wiley, 2005.
- K. Siwiak, Radiowave Propagation and Antennas for Personal Communications, Artech House, 1998.
- M.P. Doluhanov, Radiowave Propagation, Moscow: Sviaz, 1972.
- V.V. Nikolskij, T.I. Nikolskaja, Electrodynamics and Radiowave Propagation, Moscow: Nauka, 1989.
- 3GPP TR 38.901, Study on Channel Model for Frequencies from 0.5 to 100 GHz (Release 16), Sophia Antipolis, France, 2019
- Recommendation ITU-R P.1238-8: Propagation data and prediction methods for the planning of indoor radiocommunication systems and radio local area networks in the frequency range 300 MHz to 100 GHz
- S. Loyka, ELG4179: Wireless Communication Fundamentals, Lecture Notes (Lec. 2-4), University of Ottawa, Canada, 2021
| Radio frequency propagation models | |
|---|---|
| Free space | |
| Terrain | |
| Foliage | |
| Urban | |
| Indoor | |
| Other |
|


 is the transmitted signal,
is the transmitted signal,  is the length of the direct line-of-sight (LOS) ray,
is the length of the direct line-of-sight (LOS) ray,  is the length of the ground-reflected ray,
is the length of the ground-reflected ray,  is the combined antenna gain along the LOS path,
is the combined antenna gain along the LOS path,  is the combined antenna gain along the ground-reflected path,
is the combined antenna gain along the ground-reflected path,  is the wavelength of the transmission (
is the wavelength of the transmission ( , where
, where  is the
is the  is the transmission frequency),
is the transmission frequency),  is ground reflection coefficient and
is ground reflection coefficient and  is the delay spread of the model which equals
is the delay spread of the model which equals  . The ground reflection coefficient is
. The ground reflection coefficient is

 or
or  depending if the signal is horizontal or vertical polarized, respectively.
depending if the signal is horizontal or vertical polarized, respectively.  is computed as follows.
is computed as follows.

 is the relative permittivity of the ground (or generally speaking, the material where the signal is being reflected),
is the relative permittivity of the ground (or generally speaking, the material where the signal is being reflected),  is the angle between the ground and the reflected ray as shown in the figure above.
is the angle between the ground and the reflected ray as shown in the figure above.

 ,
,


 denotes average (over time) value.
denotes average (over time) value.
 , so that
, so that  , the power equation may be simplified to
, the power equation may be simplified to

 is the transmitted power.
is the transmitted power.
 is very large relative to the height of the antenna we may expand
is very large relative to the height of the antenna we may expand  ,
,

 :
:



 ,
,


 using
using 




 (angles are measured here in radians, not degrees) or, equivalently,
(angles are measured here in radians, not degrees) or, equivalently,

 . This formula was first obtained by B.A. Vvedenskij.
. This formula was first obtained by B.A. Vvedenskij.
 is called "effective isotropic radiated power" (EIRP), which is the transmit power required to produce the same received power if the transmit antenna were isotropic.
is called "effective isotropic radiated power" (EIRP), which is the transmit power required to produce the same received power if the transmit antenna were isotropic.


 or first Fresnel zone, the power drops proportionally to an inverse of fourth power of
or first Fresnel zone, the power drops proportionally to an inverse of fourth power of  and more refined analysis is required, see e.g.
and more refined analysis is required, see e.g.

 is the large-scale (log-normal) fading,
is the large-scale (log-normal) fading,  is a reference distance at which the path loss is
is a reference distance at which the path loss is  ,
,  is the path loss exponent; typically
is the path loss exponent; typically  . This model is particularly well-suited for measurements, whereby
. This model is particularly well-suited for measurements, whereby  :
:

 ,
,  , and
, and
 ,
, = the critical distance.
= the critical distance.

 and
and  are the free-space and 2-ray path losses;
are the free-space and 2-ray path losses;  is a minimum path loss (at smallest distance), usually in practice;
is a minimum path loss (at smallest distance), usually in practice;  dB or so. Note that
dB or so. Note that  and also
and also  follow from the law of energy conservation (since the Rx power cannot exceed the Tx power) so that both
follow from the law of energy conservation (since the Rx power cannot exceed the Tx power) so that both