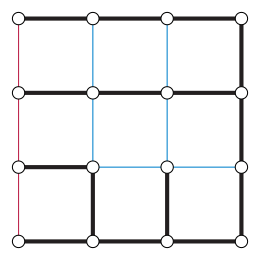
In graph theory, a Xuong tree is a spanning tree of a given graph with the property that, in the remaining graph , the number of connected components with an odd number of edges is as small as possible. They are named after Nguyen Huy Xuong, who used them to characterize the cellular embeddings of a given graph having the largest possible genus.
According to Xuong's results, if is a Xuong tree and the numbers of edges in the components of are , then the maximum genus of an embedding of is . Any one of these components, having edges, can be partitioned into edge-disjoint two-edge paths, with possibly one additional left-over edge. An embedding of maximum genus may be obtained from a planar embedding of the Xuong tree by adding each two-edge path to the embedding in such a way that it increases the genus by one.
A Xuong tree, and a maximum-genus embedding derived from it, may be found in any graph in polynomial time, by a transformation to a more general computational problem on matroids, the matroid parity problem for linear matroids.
References
- ^ Beineke, Lowell W.; Wilson, Robin J. (2009), Topics in topological graph theory, Encyclopedia of Mathematics and its Applications, vol. 128, Cambridge University Press, Cambridge, p. 36, doi:10.1017/CBO9781139087223, ISBN 978-0-521-80230-7, MR 2581536
- ^ Xuong, Nguyen Huy (1979), "How to determine the maximum genus of a graph", Journal of Combinatorial Theory, Series B, 26 (2): 217–225, doi:10.1016/0095-8956(79)90058-3, MR 0532589
- Sumner, David P. (1974), "Graphs with 1-factors", Proceedings of the American Mathematical Society, 42 (1), American Mathematical Society: 8–12, doi:10.2307/2039666, JSTOR 2039666, MR 0323648
- Furst, Merrick L.; Gross, Jonathan L.; McGeoch, Lyle A. (1988), "Finding a maximum-genus graph imbedding", Journal of the ACM, 35 (3): 523–534, doi:10.1145/44483.44485, MR 0963159, S2CID 17991210
 of a given graph
of a given graph  with the property that, in the remaining graph
with the property that, in the remaining graph  , the number of
, the number of  , then the maximum genus of an embedding of
, then the maximum genus of an embedding of  .
Any one of these components, having
.
Any one of these components, having  edges, can be partitioned into
edges, can be partitioned into  edge-disjoint two-edge paths, with possibly one additional left-over edge.
An embedding of maximum genus may be obtained from a planar embedding of the Xuong tree by adding each two-edge path to the embedding in such a way that it increases the genus by one.
edge-disjoint two-edge paths, with possibly one additional left-over edge.
An embedding of maximum genus may be obtained from a planar embedding of the Xuong tree by adding each two-edge path to the embedding in such a way that it increases the genus by one.