In mathematics, Pascal's triangle is an infinite triangular array of the binomial coefficients which play a crucial role in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy.
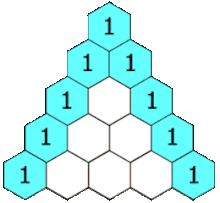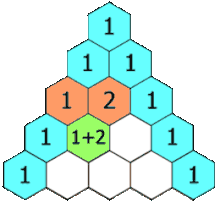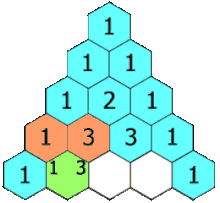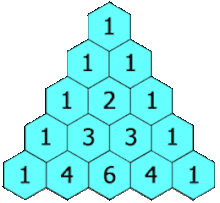
The rows of Pascal's triangle are conventionally enumerated starting with row at the top (the 0th row). The entries in each row are numbered from the left beginning with and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas the numbers 1 and 3 in row 3 are added to produce the number 4 in row 4.
Formula
In the th row of Pascal's triangle, the th entry is denoted , pronounced "n choose k". For example, the topmost entry is . With this notation, the construction of the previous paragraph may be written as
for any positive integer and any integer . This recurrence for the binomial coefficients is known as Pascal's rule.
History


The pattern of numbers that forms Pascal's triangle was known well before Pascal's time. The Persian mathematician Al-Karaji (953–1029) wrote a now-lost book which contained the first description of Pascal's triangle. In India, the Chandaḥśāstra by the Indian lyricist Piṅgala (3rd or 2nd century BC) somewhat crypically describes a method of arranging two types of syllables to form metres of various lengths and counting them; as interpreted and elaborated by Piṅgala's 10th-century commentator Halāyudha his "method of pyramidal expansion" (meru-prastāra) for counting metres is equivalent to Pascal's triangle. It was later repeated by Omar Khayyám (1048–1131), another Persian mathematician; thus the triangle is also referred to as Khayyam's triangle (مثلث خیام) in Iran. Several theorems related to the triangle were known, including the binomial theorem. Khayyam used a method of finding nth roots based on the binomial expansion, and therefore on the binomial coefficients.
Pascal's triangle was known in China during the 11th century through the work of the Chinese mathematician Jia Xian (1010–1070). During the 13th century, Yang Hui (1238–1298) defined the triangle, and it is known as Yang Hui's triangle (杨辉三角; 楊輝三角) in China.
In Europe, Pascal's triangle appeared for the first time in the Arithmetic of Jordanus de Nemore (13th century). The binomial coefficients were calculated by Gersonides during the early 14th century, using the multiplicative formula for them. Petrus Apianus (1495–1552) published the full triangle on the frontispiece of his book on business calculations in 1527. Michael Stifel published a portion of the triangle (from the second to the middle column in each row) in 1544, describing it as a table of figurate numbers. In Italy, Pascal's triangle is referred to as Tartaglia's triangle, named for the Italian algebraist Tartaglia (1500–1577), who published six rows of the triangle in 1556. Gerolamo Cardano also published the triangle as well as the additive and multiplicative rules for constructing it in 1570.
Pascal's Traité du triangle arithmétique (Treatise on Arithmetical Triangle) was published posthumously in 1665. In this, Pascal collected several results then known about the triangle, and employed them to solve problems in probability theory. The triangle was later named for Pascal by Pierre Raymond de Montmort (1708) who called it table de M. Pascal pour les combinaisons (French: Mr. Pascal's table for combinations) and Abraham de Moivre (1730) who called it Triangulum Arithmeticum PASCALIANUM (Latin: Pascal's Arithmetic Triangle), which became the basis of the modern Western name.
Binomial expansions

Pascal's triangle determines the coefficients which arise in binomial expansions. For example, in the expansion the coefficients are the entries in the second row of Pascal's triangle: , , .
In general, the binomial theorem states that when a binomial like is raised to a positive integer power , the expression expands as where the coefficients are precisely the numbers in row of Pascal's triangle:
The entire left diagonal of Pascal's triangle corresponds to the coefficient of in these binomial expansions, while the next left diagonal corresponds to the coefficient of , and so on.
To see how the binomial theorem relates to the simple construction of Pascal's triangle, consider the problem of calculating the coefficients of the expansion of in terms of the corresponding coefficients of , where we set for simplicity. Suppose then that Now
The first six rows of Pascal's triangle as binomial coefficientsThe two summations can be reindexed with and combined to yield
Thus the extreme left and right coefficients remain as 1, and for any given , the coefficient of the term in the polynomial is equal to , the sum of the and coefficients in the previous power . This is indeed the downward-addition rule for constructing Pascal's triangle.
It is not difficult to turn this argument into a proof (by mathematical induction) of the binomial theorem.
Since , the coefficients are identical in the expansion of the general case.
An interesting consequence of the binomial theorem is obtained by setting both variables , so that
In other words, the sum of the entries in the th row of Pascal's triangle is the th power of 2. This is equivalent to the statement that the number of subsets of an -element set is , as can be seen by observing that each of the elements may be independently included or excluded from a given subset.
Combinations
A second useful application of Pascal's triangle is in the calculation of combinations. The number of combinations of items taken at a time, i.e. the number of subsets of elements from among elements, can be found by the equation
- .
This is equal to entry in row of Pascal's triangle. Rather than performing the multiplicative calculation, one can simply look up the appropriate entry in the triangle (constructed by additions). For example, suppose 3 workers need to be hired from among 7 candidates; then the number of possible hiring choices is 7 choose 3, the entry 3 in row 7 of the above table (taking into consideration the first row is the 0th row), which is .
Relation to binomial distribution and convolutions
When divided by , the th row of Pascal's triangle becomes the binomial distribution in the symmetric case where . By the central limit theorem, this distribution approaches the normal distribution as increases. This can also be seen by applying Stirling's formula to the factorials involved in the formula for combinations.
This is related to the operation of discrete convolution in two ways. First, polynomial multiplication corresponds exactly to discrete convolution, so that repeatedly convolving the sequence with itself corresponds to taking powers of , and hence to generating the rows of the triangle. Second, repeatedly convolving the distribution function for a random variable with itself corresponds to calculating the distribution function for a sum of n independent copies of that variable; this is exactly the situation to which the central limit theorem applies, and hence results in the normal distribution in the limit. (The operation of repeatedly taking a convolution of something with itself is called the convolution power.)
Patterns and properties
Pascal's triangle has many properties and contains many patterns of numbers.


Rows
- The sum of the elements of a single row is twice the sum of the row preceding it. For example, row 0 (the topmost row) has a value of 1, row 1 has a value of 2, row 2 has a value of 4, and so forth. This is because every item in a row produces two items in the next row: one left and one right. The sum of the elements of row equals to .
- Taking the product of the elements in each row, the sequence of products (sequence A001142 in the OEIS) is related to the base of the natural logarithm, e. Specifically, define the sequence for all as follows: Then, the ratio of successive row products is and the ratio of these ratios is The right-hand side of the above equation takes the form of the limit definition of .
- can be found in Pascal's triangle by use of the Nilakantha infinite series.
- Some of the numbers in Pascal's triangle correlate to numbers in Lozanić's triangle.
- The sum of the squares of the elements of row n equals the middle element of row 2n. For example, 1 + 4 + 6 + 4 + 1 = 70. In general form,
- In any even row , the middle term minus the term two spots to the left equals a Catalan number, specifically . For example, in row 4, which is 1, 4, 6, 4, 1, we get the 3rd Catalan number .
- In a row p, where p is a prime number, all the terms in that row except the 1s are divisible by p. This can be proven easily, from the multiplicative formula . Since the denominator can have no prime factors equal to p, so p remains in the numerator after integer division, making the entire entry a multiple of p.
- Parity: To count odd terms in row n, convert n to binary. Let x be the number of 1s in the binary representation. Then the number of odd terms will be 2. These numbers are the values in Gould's sequence.
- Every entry in row 2 − 1, n ≥ 0, is odd.
- Polarity: When the elements of a row of Pascal's triangle are alternately added and subtracted together, the result is 0. For example, row 6 is 1, 6, 15, 20, 15, 6, 1, so the formula is 1 − 6 + 15 − 20 + 15 − 6 + 1 = 0.
Diagonals

The diagonals of Pascal's triangle contain the figurate numbers of simplices:
- The diagonals going along the left and right edges contain only 1's.
- The diagonals next to the edge diagonals contain the natural numbers in order. The 1-dimensional simplex numbers increment by 1 as the line segments extend to the next whole number along the number line.
- Moving inwards, the next pair of diagonals contain the triangular numbers in order.
- The next pair of diagonals contain the tetrahedral numbers in order, and the next pair give pentatope numbers.
The symmetry of the triangle implies that the n d-dimensional number is equal to the d n-dimensional number.
An alternative formula that does not involve recursion is where n is the rising factorial.
The geometric meaning of a function Pd is: Pd(1) = 1 for all d. Construct a d-dimensional triangle (a 3-dimensional triangle is a tetrahedron) by placing additional dots below an initial dot, corresponding to Pd(1) = 1. Place these dots in a manner analogous to the placement of numbers in Pascal's triangle. To find Pd(x), have a total of x dots composing the target shape. Pd(x) then equals the total number of dots in the shape. A 0-dimensional triangle is a point and a 1-dimensional triangle is simply a line, and therefore P0(x) = 1 and P1(x) = x, which is the sequence of natural numbers. The number of dots in each layer corresponds to Pd − 1(x).
Calculating a row or diagonal by itself
There are simple algorithms to compute all the elements in a row or diagonal without computing other elements or factorials.
To compute row with the elements , begin with . For each subsequent element, the value is determined by multiplying the previous value by a fraction with slowly changing numerator and denominator:
For example, to calculate row 5, the fractions are , , , and , and hence the elements are , , , etc. (The remaining elements are most easily obtained by symmetry.)
To compute the diagonal containing the elements begin again with and obtain subsequent elements by multiplication by certain fractions:
For example, to calculate the diagonal beginning at , the fractions are , and the elements are , etc. By symmetry, these elements are equal to , etc.

Overall patterns and properties

- The pattern obtained by coloring only the odd numbers in Pascal's triangle closely resembles the fractal known as the Sierpinski triangle. This resemblance becomes increasingly accurate as more rows are considered; in the limit, as the number of rows approaches infinity, the resulting pattern is the Sierpinski triangle, assuming a fixed perimeter. More generally, numbers could be colored differently according to whether or not they are multiples of 3, 4, etc.; this results in other similar patterns.
- As the proportion of black numbers tends to zero with increasing n, a corollary is that the proportion of odd binomial coefficients tends to zero as n tends to infinity.
| 10 | |||
| 10 | 20 |
Pascal's triangle overlaid on a grid gives the number of distinct paths to each square, assuming only rightward and downward steps to an adjacent square are considered.
- In a triangular portion of a grid (as in the images below), the number of shortest grid paths from a given node to the top node of the triangle is the corresponding entry in Pascal's triangle. On a Plinko game board shaped like a triangle, this distribution should give the probabilities of winning the various prizes.

- If the rows of Pascal's triangle are left-justified, the diagonal bands (colour-coded below) sum to the Fibonacci numbers.
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1
Construction as matrix exponential
Binomial matrix as matrix exponential. All the dots represent 0. See also: Pascal matrixDue to its simple construction by factorials, a very basic representation of Pascal's triangle in terms of the matrix exponential can be given: Pascal's triangle is the exponential of the matrix which has the sequence 1, 2, 3, 4, ... on its sub-diagonal and zero everywhere else.
Construction of Clifford algebra using simplices
Labelling the elements of each n-simplex matches the basis elements of Clifford algebra used as forms in Geometric Algebra rather than matrices. Recognising the geometric operations, such as rotations, allows the algebra operations to be discovered. Just as each row, n, starting at 0, of Pascal's triangle corresponds to an (n-1)-simplex, as described below, it also defines the number of named basis forms in n dimensional Geometric algebra. The binomial theorem can be used to prove the geometric relationship provided by Pascal's triangle. This same proof could be applied to simplices except that the first column of all 1's must be ignored whereas in the algebra these correspond to the real numbers, , with basis 1.
Relation to geometry of polytopes
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (October 2016) (Learn how and when to remove this message) |
Pascal's triangle can be used as a lookup table for the number of elements (such as edges and corners) within a polytope (such as a triangle, a tetrahedron, a square, or a cube).
Number of elements of simplices
Let's begin by considering the 3rd line of Pascal's triangle, with values 1, 3, 3, 1. A 2-dimensional triangle has one 2-dimensional element (itself), three 1-dimensional elements (lines, or edges), and three 0-dimensional elements (vertices, or corners). The meaning of the final number (1) is more difficult to explain (but see below). Continuing with our example, a tetrahedron has one 3-dimensional element (itself), four 2-dimensional elements (faces), six 1-dimensional elements (edges), and four 0-dimensional elements (vertices). Adding the final 1 again, these values correspond to the 4th row of the triangle (1, 4, 6, 4, 1). Line 1 corresponds to a point, and Line 2 corresponds to a line segment (dyad). This pattern continues to arbitrarily high-dimensioned hyper-tetrahedrons (known as simplices).
To understand why this pattern exists, one must first understand that the process of building an n-simplex from an (n − 1)-simplex consists of simply adding a new vertex to the latter, positioned such that this new vertex lies outside of the space of the original simplex, and connecting it to all original vertices. As an example, consider the case of building a tetrahedron from a triangle, the latter of whose elements are enumerated by row 3 of Pascal's triangle: 1 face, 3 edges, and 3 vertices. To build a tetrahedron from a triangle, position a new vertex above the plane of the triangle and connect this vertex to all three vertices of the original triangle.
The number of a given dimensional element in the tetrahedron is now the sum of two numbers: first the number of that element found in the original triangle, plus the number of new elements, each of which is built upon elements of one fewer dimension from the original triangle. Thus, in the tetrahedron, the number of cells (polyhedral elements) is 0 + 1 = 1; the number of faces is 1 + 3 = 4; the number of edges is 3 + 3 = 6; the number of new vertices is 3 + 1 = 4. This process of summing the number of elements of a given dimension to those of one fewer dimension to arrive at the number of the former found in the next higher simplex is equivalent to the process of summing two adjacent numbers in a row of Pascal's triangle to yield the number below. Thus, the meaning of the final number (1) in a row of Pascal's triangle becomes understood as representing the new vertex that is to be added to the simplex represented by that row to yield the next higher simplex represented by the next row. This new vertex is joined to every element in the original simplex to yield a new element of one higher dimension in the new simplex, and this is the origin of the pattern found to be identical to that seen in Pascal's triangle.
Number of elements of hypercubes
A similar pattern is observed relating to squares, as opposed to triangles. To find the pattern, one must construct an analog to Pascal's triangle, whose entries are the coefficients of (x + 2), instead of (x + 1). There are a couple ways to do this. The simpler is to begin with row 0 = 1 and row 1 = 1, 2. Proceed to construct the analog triangles according to the following rule:
That is, choose a pair of numbers according to the rules of Pascal's triangle, but double the one on the left before adding. This results in:
The other way of producing this triangle is to start with Pascal's triangle and multiply each entry by 2, where k is the position in the row of the given number. For example, the 2nd value in row 4 of Pascal's triangle is 6 (the slope of 1s corresponds to the zeroth entry in each row). To get the value that resides in the corresponding position in the analog triangle, multiply 6 by 2 = 6 × 2 = 6 × 4 = 24. Now that the analog triangle has been constructed, the number of elements of any dimension that compose an arbitrarily dimensioned cube (called a hypercube) can be read from the table in a way analogous to Pascal's triangle. For example, the number of 2-dimensional elements in a 2-dimensional cube (a square) is one, the number of 1-dimensional elements (sides, or lines) is 4, and the number of 0-dimensional elements (points, or vertices) is 4. This matches the 2nd row of the table (1, 4, 4). A cube has 1 cube, 6 faces, 12 edges, and 8 vertices, which corresponds to the next line of the analog triangle (1, 6, 12, 8). This pattern continues indefinitely.
To understand why this pattern exists, first recognize that the construction of an n-cube from an (n − 1)-cube is done by simply duplicating the original figure and displacing it some distance (for a regular n-cube, the edge length) orthogonal to the space of the original figure, then connecting each vertex of the new figure to its corresponding vertex of the original. This initial duplication process is the reason why, to enumerate the dimensional elements of an n-cube, one must double the first of a pair of numbers in a row of this analog of Pascal's triangle before summing to yield the number below. The initial doubling thus yields the number of "original" elements to be found in the next higher n-cube and, as before, new elements are built upon those of one fewer dimension (edges upon vertices, faces upon edges, etc.). Again, the last number of a row represents the number of new vertices to be added to generate the next higher n-cube.
In this triangle, the sum of the elements of row m is equal to 3. Again, to use the elements of row 4 as an example: 1 + 8 + 24 + 32 + 16 = 81, which is equal to .
Counting vertices in a cube by distance
Each row of Pascal's triangle gives the number of vertices at each distance from a fixed vertex in an n-dimensional cube. For example, in three dimensions, the third row (1 3 3 1) corresponds to the usual three-dimensional cube: fixing a vertex V, there is one vertex at distance 0 from V (that is, V itself), three vertices at distance 1, three vertices at distance √2 and one vertex at distance √3 (the vertex opposite V). The second row corresponds to a square, while larger-numbered rows correspond to hypercubes in each dimension.
Fourier transform of sin(x)/x
As stated previously, the coefficients of (x + 1) are the nth row of the triangle. Now the coefficients of (x − 1) are the same, except that the sign alternates from +1 to −1 and back again. After suitable normalization, the same pattern of numbers occurs in the Fourier transform of sin(x)/x. More precisely: if n is even, take the real part of the transform, and if n is odd, take the imaginary part. Then the result is a step function, whose values (suitably normalized) are given by the nth row of the triangle with alternating signs. For example, the values of the step function that results from:
compose the 4th row of the triangle, with alternating signs. This is a generalization of the following basic result (often used in electrical engineering):
is the boxcar function. The corresponding row of the triangle is row 0, which consists of just the number 1.
If n is congruent to 2 or to 3 mod 4, then the signs start with −1. In fact, the sequence of the (normalized) first terms corresponds to the powers of i, which cycle around the intersection of the axes with the unit circle in the complex plane:
Extensions
Pascal's triangle may be extended upwards, above the 1 at the apex, preserving the additive property, but there is more than one way to do so.
To higher dimensions
Pascal's triangle has higher dimensional generalizations. The three-dimensional version is known as Pascal's pyramid or Pascal's tetrahedron, while the general versions are known as Pascal's simplices.
To complex numbers
When the factorial function is defined as , Pascal's triangle can be extended beyond the integers to , since is meromorphic to the entire complex plane.
To arbitrary bases
Isaac Newton once observed that the first five rows of Pascal's triangle, when read as the digits of an integer, are the corresponding powers of eleven. He claimed without proof that subsequent rows also generate powers of eleven. In 1964, Robert L. Morton presented the more generalized argument that each row can be read as a radix numeral, where is the hypothetical terminal row, or limit, of the triangle, and the rows are its partial products. He proved the entries of row , when interpreted directly as a place-value numeral, correspond to the binomial expansion of . More rigorous proofs have since been developed. To better understand the principle behind this interpretation, here are some things to recall about binomials:
- A radix numeral in positional notation (e.g. ) is a univariate polynomial in the variable , where the degree of the variable of the th term (starting with ) is . For example, .
- A row corresponds to the binomial expansion of . The variable can be eliminated from the expansion by setting . The expansion now typifies the expanded form of a radix numeral, as demonstrated above. Thus, when the entries of the row are concatenated and read in radix they form the numerical equivalent of . If for , then the theorem holds for with odd values of yielding negative row products.
By setting the row's radix (the variable ) equal to one and ten, row becomes the product and , respectively. To illustrate, consider , which yields the row product . The numeric representation of is formed by concatenating the entries of row . The twelfth row denotes the product:
with compound digits (delimited by ":") in radix twelve. The digits from through are compound because these row entries compute to values greater than or equal to twelve. To normalize the numeral, simply carry the first compound entry's prefix, that is, remove the prefix of the coefficient from its leftmost digit up to, but excluding, its rightmost digit, and use radix-twelve arithmetic to sum the removed prefix with the entry on its immediate left, then repeat this process, proceeding leftward, until the leftmost entry is reached. In this particular example, the normalized string ends with for all . The leftmost digit is for , which is obtained by carrying the of at entry . It follows that the length of the normalized value of is equal to the row length, . The integral part of contains exactly one digit because (the number of places to the left the decimal has moved) is one less than the row length. Below is the normalized value of . Compound digits remain in the value because they are radix residues represented in radix ten:
See also
- Bean machine, Francis Galton's "quincunx"
- Bell triangle
- Bernoulli's triangle
- Binomial expansion
- Cellular automata
- Euler triangle
- Floyd's triangle
- Gaussian binomial coefficient
- Hockey-stick identity
- Leibniz harmonic triangle
- Multiplicities of entries in Pascal's triangle (Singmaster's conjecture)
- Pascal matrix
- Pascal's pyramid
- Pascal's simplex
- Proton NMR, one application of Pascal's triangle
- Star of David theorem
- Trinomial expansion
- Trinomial triangle
- Polynomials calculating sums of powers of arithmetic progressions
References
- ^ Coolidge, J. L. (1949), "The story of the binomial theorem", The American Mathematical Monthly, 56 (3): 147–157, doi:10.2307/2305028, JSTOR 2305028, MR 0028222.
- Maurice Winternitz, History of Indian Literature, Vol. III
- Peter Fox (1998). Cambridge University Library: the great collections. Cambridge University Press. p. 13. ISBN 978-0-521-62647-7.
- The binomial coefficient is conventionally set to zero if k is either less than zero or greater than n.
- Selin, Helaine (2008-03-12). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. Springer Science & Business Media. p. 132. Bibcode:2008ehst.book.....S. ISBN 9781402045592.
Other, lost works of al-Karaji's are known to have dealt with inderterminate algebra, arithmetic, inheritance algebra, and the construction of buildings. Another contained the first known explanation of the arithmetical (Pascal's) triangle; the passage in question survived through al-Sama'wal's Bahir (twelfth century) which heavily drew from the Badi.
- Rashed, R. (1994-06-30). The Development of Arabic Mathematics: Between Arithmetic and Algebra. Springer Science & Business Media. p. 63. ISBN 978-0-7923-2565-9.
- Sidoli, Nathan; Brummelen, Glen Van (2013-10-30). From Alexandria, Through Baghdad: Surveys and Studies in the Ancient Greek and Medieval Islamic Mathematical Sciences in Honor of J.L. Berggren. Springer Science & Business Media. p. 54. ISBN 9783642367366.
However, the use of binomial coefficients by Islamic mathematicians of the eleventh century, in a context which had deep roots in Islamic mathematics, suggests strongly the table was a local discovery - most probably of al-Karaji."
- Alsdorf, Ludwig (1991) . "The Pratyayas: Indian Contribution to Combinatorics" (PDF). Indian Journal of History of Science. 26 (1): 17–61. Translated by S. R. Sarma from "π Die Pratyayas. Ein Beitrag zur indischen Mathematik". Zeitschrift fur Indologie und Iranistik. 9: 97–157. 1933. Bag, Amulya Kumar (1966). "Binomial theorem in ancient India" (PDF). Indian Journal of History of Science. 1 (1): 68–74. Tertiary sources: Sen, Samarendra Nath (1971). "Mathematics". In Bose, D. M. (ed.). A Concise History Of Science In India. Indian National Science Academy. Ch. 3, pp. 136–212, esp. "Permutations, Combinations and Pascal Triangle", pp. 156–157. Fowler, David H. (1996). "The Binomial Coefficient Function". The American Mathematical Monthly. 103 (1): 1–17, esp. §4 "A Historical Note", pp. 10–17. doi:10.2307/2975209. JSTOR 2975209.
- Kennedy, E. (1966). Omar Khayyam. The Mathematics Teacher 1958. National Council of Teachers of Mathematics. pp. 140–142. JSTOR i27957284.
- Weisstein, Eric W. (2003). CRC concise encyclopedia of mathematics, p. 2169. ISBN 978-1-58488-347-0.
- Hughes, Barnabas (1 August 1989). "The arithmetical triangle of Jordanus de Nemore". Historia Mathematica. 16 (3): 213–223. doi:10.1016/0315-0860(89)90018-9.
- ^ Edwards, A. W. F. (2013), "The arithmetical triangle", in Wilson, Robin; Watkins, John J. (eds.), Combinatorics: Ancient and Modern, Oxford University Press, pp. 166–180.
- Smith, Karl J. (2010), Nature of Mathematics, Cengage Learning, p. 10, ISBN 9780538737586.
- Pascal, Blaise (1623-1662) Auteur du texte (1665). Traité du triangle arithmétique , avec quelques autres petits traitez sur la mesme matière. Par Monsieur Pascal.
{{cite book}}: CS1 maint: numeric names: authors list (link) - Fowler, David (January 1996). "The Binomial Coefficient Function". The American Mathematical Monthly. 103 (1): 1–17. doi:10.2307/2975209. JSTOR 2975209. See in particular p. 11.
- "Pascal's Triangle in Probability". 5010.mathed.usu.edu. Retrieved 2023-06-01.
- Brothers, H. J. (2012), "Finding e in Pascal's triangle", Mathematics Magazine, 85: 51, doi:10.4169/math.mag.85.1.51, S2CID 218541210.
- Brothers, H. J. (2012), "Pascal's triangle: The hidden stor-e", The Mathematical Gazette, 96: 145–148, doi:10.1017/S0025557200004204, S2CID 233356674.
- Foster, T. (2014), "Nilakantha's Footprints in Pascal's Triangle", Mathematics Teacher, 108: 247, doi:10.5951/mathteacher.108.4.0246
- Fine, N. J. (1947), "Binomial coefficients modulo a prime", American Mathematical Monthly, 54 (10): 589–592, doi:10.2307/2304500, JSTOR 2304500, MR 0023257. See in particular Theorem 2, which gives a generalization of this fact for all prime moduli.
- Hinz, Andreas M. (1992), "Pascal's triangle and the Tower of Hanoi", The American Mathematical Monthly, 99 (6): 538–544, doi:10.2307/2324061, JSTOR 2324061, MR 1166003. Hinz attributes this observation to an 1891 book by Édouard Lucas, Théorie des nombres (p. 420).
- Ian Stewart, "How to Cut a Cake", Oxford University Press, page 180
- Wilmot, G.P. (2023), The Algebra Of Geometry
- Coxeter, Harold Scott Macdonald (1973-01-01). "Chapter VII: ordinary polytopes in higher space, 7.2: Pyramids, dipyramids and prisms". Regular Polytopes (3rd ed.). Courier Corporation. pp. 118–144. ISBN 978-0-486-61480-9.
- For a similar example, see e.g. Hore, P. J. (1983), "Solvent suppression in Fourier transform nuclear magnetic resonance", Journal of Magnetic Resonance, 55 (2): 283–300, Bibcode:1983JMagR..55..283H, doi:10.1016/0022-2364(83)90240-8.
- Karl, John H. (2012), An Introduction to Digital Signal Processing, Elsevier, p. 110, ISBN 9780323139595.
- Hilton, P.; et al. (1989). "Extending the binomial coefficients to preserve symmetry and pattern". Symmetry 2. In International Series in Modern Applied Mathematics and Computer Science. Pergamon. pp. 89–102. doi:10.1016/B978-0-08-037237-2.50013-1. ISBN 9780080372372..
- Hilton, P.; et al. (1989). "Extending the binomial coefficients to preserve symmetry and pattern". Symmetry 2. In International Series in Modern Applied Mathematics and Computer Science. Pergamon. pp. 100–102. doi:10.1016/B978-0-08-037237-2.50013-1. ISBN 9780080372372..
- Newton, Isaac (1736), "A Treatise of the Method of Fluxions and Infinite Series", The Mathematical Works of Isaac Newton: 1:31–33,
But these in the alternate areas, which are given, I observed were the same with the figures of which the several ascending powers of the number 11 consist, viz. , , , , , etc. that is, first 1; the second 1, 1; the third 1, 2, 1; the fourth 1, 3, 3, 1; the fifth 1, 4, 6, 4, 1, and so on
. - Morton, Robert L. (1964), "Pascal's Triangle and powers of 11", The Mathematics Teacher, 57 (6): 392–394, doi:10.5951/MT.57.6.0392, JSTOR 27957091.
- Arnold, Robert; et al. (2004), "Newton's Unfinished Business: Uncovering the Hidden Powers of Eleven in Pascal's Triangle", Proceedings of Undergraduate Mathematics Day.
- Islam, Robiul; et al. (2020), Finding any row of Pascal's triangle extending the concept of power of 11.
- Winteridge, David J. (1984), "Pascal's Triangle and Powers of 11", Mathematics in School, 13 (1): 12–13, JSTOR 30213884.
- Kallós, Gábor (2006), "A generalization of Pascal's triangle using powers of base numbers" (PDF), Annales Mathématiques, 13 (1): 1–15, doi:10.5802/ambp.211.
- Hilton, P.; et al. (1989). "Extending the binomial coefficients to preserve symmetry and pattern". Symmetry 2. In International Series in Modern Applied Mathematics and Computer Science. Pergamon. pp. 89–91. doi:10.1016/B978-0-08-037237-2.50013-1. ISBN 9780080372372..
- Mueller, Francis J. (1965), "More on Pascal's Triangle and powers of 11", The Mathematics Teacher, 58 (5): 425–428, doi:10.5951/MT.58.5.0425, JSTOR 27957164.
- Low, Leone (1966), "Even more on Pascal's Triangle and Powers of 11", The Mathematics Teacher, 59 (5): 461–463, doi:10.5951/MT.59.5.0461, JSTOR 27957385.
- Fjelstad, P. (1991), "Extending Pascal's Triangle", Computers & Mathematics with Applications, 21 (9): 3, doi:10.1016/0898-1221(91)90119-O.
External links
- "Pascal triangle", Encyclopedia of Mathematics, EMS Press, 2001
- Weisstein, Eric W. "Pascal's triangle". MathWorld.
- The Old Method Chart of the Seven Multiplying Squares (from the Ssu Yuan Yü Chien of Chu Shi-Chieh, 1303, depicting the first nine rows of Pascal's triangle)
- Pascal's Treatise on the Arithmetic Triangle (page images of Pascal's treatise, 1654; summary)
| Blaise Pascal | |
|---|---|
| |
| Works |
|
| Family |
|
 A diagram showing the first eight rows of Pascal's triangle.
A diagram showing the first eight rows of Pascal's triangle. at the top (the 0th row). The entries in each row are numbered from the left beginning with
at the top (the 0th row). The entries in each row are numbered from the left beginning with  and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas the numbers 1 and 3 in row 3 are added to produce the number 4 in row 4.
and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row 0 (the topmost row), there is a unique nonzero entry 1. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as 0. For example, the initial number of row 1 (or any other row) is 1 (the sum of 0 and 1), whereas the numbers 1 and 3 in row 3 are added to produce the number 4 in row 4.
 th row of Pascal's triangle, the
th row of Pascal's triangle, the  th entry is denoted
th entry is denoted  , pronounced "n choose k". For example, the topmost entry is
, pronounced "n choose k". For example, the topmost entry is  . With this notation, the construction of the previous paragraph may be written as
. With this notation, the construction of the previous paragraph may be written as
 for any positive integer
for any positive integer  . This recurrence for the binomial coefficients is known as
. This recurrence for the binomial coefficients is known as  the coefficients are the entries in the second row of Pascal's triangle:
the coefficients are the entries in the second row of Pascal's triangle:  ,
,  ,
,  .
.
 is raised to a positive integer power
is raised to a positive integer power  where the coefficients
where the coefficients  are precisely the numbers in row
are precisely the numbers in row 
 in these binomial expansions, while the next left diagonal corresponds to the coefficient of
in these binomial expansions, while the next left diagonal corresponds to the coefficient of  , and so on.
, and so on.
 in terms of the corresponding coefficients of
in terms of the corresponding coefficients of  , where we set
, where we set  for simplicity. Suppose then that
for simplicity. Suppose then that
 Now
Now

 The first six rows of Pascal's triangle as binomial coefficients
The first six rows of Pascal's triangle as binomial coefficients
 and combined to yield
and combined to yield

 , the coefficient of the
, the coefficient of the  term in the polynomial
term in the polynomial  is equal to
is equal to  , the sum of the
, the sum of the  and
and  , the coefficients are identical in the expansion of the general case.
, the coefficients are identical in the expansion of the general case.
 , so that
, so that

 , as can be seen by observing that each of the
, as can be seen by observing that each of the  .
. .
.
 . By the
. By the  with itself corresponds to taking powers of
with itself corresponds to taking powers of  , and hence to generating the rows of the triangle. Second, repeatedly convolving the distribution function for a
, and hence to generating the rows of the triangle. Second, repeatedly convolving the distribution function for a  for all
for all  as follows:
as follows:  Then, the ratio of successive row products is
Then, the ratio of successive row products is  and the ratio of these ratios is
and the ratio of these ratios is  The right-hand side of the above equation takes the form of the limit definition of
The right-hand side of the above equation takes the form of the limit definition of 
 .
.


 , the middle term minus the term two spots to the left equals a
, the middle term minus the term two spots to the left equals a  . For example, in row 4, which is 1, 4, 6, 4, 1, we get the 3rd Catalan number
. For example, in row 4, which is 1, 4, 6, 4, 1, we get the 3rd Catalan number  .
. . Since the denominator
. Since the denominator  can have no prime factors equal to p, so p remains in the numerator after integer division, making the entire entry a multiple of p.
can have no prime factors equal to p, so p remains in the numerator after integer division, making the entire entry a multiple of p.
 where n is the
where n is the  , begin with
, begin with  . For each subsequent element, the value is determined by multiplying the previous value by a fraction with slowly changing numerator and denominator:
. For each subsequent element, the value is determined by multiplying the previous value by a fraction with slowly changing numerator and denominator:

 ,
,  ,
,  ,
,  and
and  , and hence the elements are
, and hence the elements are  ,
,  ,
,  , etc. (The remaining elements are most easily obtained by symmetry.)
, etc. (The remaining elements are most easily obtained by symmetry.)
 begin again with
begin again with 
 , the fractions are
, the fractions are  , and the elements are
, and the elements are  , etc. By symmetry, these elements are equal to
, etc. By symmetry, these elements are equal to  , etc.
, etc.
 Binomial matrix as matrix exponential. All the dots represent 0.
See also:
Binomial matrix as matrix exponential. All the dots represent 0.
See also:  , with basis 1.
, with basis 1.


 .
.



 , Pascal's triangle can be extended beyond the integers to
, Pascal's triangle can be extended beyond the integers to  , since
, since  is
is  numeral, where
numeral, where 
 . More rigorous proofs have since been developed. To better understand the principle behind this interpretation, here are some things to recall about binomials:
. More rigorous proofs have since been developed. To better understand the principle behind this interpretation, here are some things to recall about binomials:
 ) is a univariate polynomial in the variable
) is a univariate polynomial in the variable  th
th  ) is
) is  .
. . The variable
. The variable  can be eliminated from the expansion by setting
can be eliminated from the expansion by setting  . The expansion now typifies the expanded form of a radix
. The expansion now typifies the expanded form of a radix  for
for  , then the theorem
, then the theorem  with odd values of
with odd values of  and
and  , respectively. To illustrate, consider
, respectively. To illustrate, consider  , which yields the row product
, which yields the row product  . The numeric representation of
. The numeric representation of 

 through
through  are compound because these row entries compute to values greater than or equal to twelve. To
are compound because these row entries compute to values greater than or equal to twelve. To  from its leftmost digit up to, but excluding, its rightmost digit, and use radix-twelve arithmetic to sum the removed prefix with the entry on its immediate left, then repeat this process, proceeding leftward, until the leftmost entry is reached. In this particular example, the normalized string ends with
from its leftmost digit up to, but excluding, its rightmost digit, and use radix-twelve arithmetic to sum the removed prefix with the entry on its immediate left, then repeat this process, proceeding leftward, until the leftmost entry is reached. In this particular example, the normalized string ends with  for all
for all  for
for  , which is obtained by carrying the
, which is obtained by carrying the  of
of  at entry
at entry  . The integral part of
. The integral part of  contains exactly one digit because
contains exactly one digit because  . Compound digits remain in the value because they are radix
. Compound digits remain in the value because they are radix 

 is conventionally set to zero if k is either less than zero or greater than n.
is conventionally set to zero if k is either less than zero or greater than n.
 ,
,  ,
,  ,
,  ,
,  , etc. that is, first 1; the second 1, 1; the third 1, 2, 1; the fourth 1, 3, 3, 1; the fifth 1, 4, 6, 4, 1, and so on
, etc. that is, first 1; the second 1, 1; the third 1, 2, 1; the fourth 1, 3, 3, 1; the fifth 1, 4, 6, 4, 1, and so on