| Revision as of 09:19, 24 March 2021 editSecret0700000 (talk | contribs)2 edits →Geometric constructionTags: Reverted Possible vandalism← Previous edit | Latest revision as of 10:45, 30 December 2023 edit undoFehufanga (talk | contribs)Edit filter helpers, Extended confirmed users, Pending changes reviewers, Rollbackers30,922 editsm Reverted edits by 183.171.191.246 (talk) to last revision by Euro2023: nonconstructive editsTags: Rollback SWViewer [1.6] | ||
| (16 intermediate revisions by 12 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Compromise map projection}} | |||
| ] | ] | ||
| ] of deformation]] | ] of deformation]] | ||
| The '''van der Grinten projection''' is a compromise ], which means that it is neither ] nor ]. Unlike perspective projections, the van der Grinten projection is an arbitrary geometric construction on the plane. Van der Grinten projects the entire Earth into a circle. It largely preserves the familiar shapes of the ] while modestly reducing Mercator's distortion. Polar regions are subject to extreme distortion.<ref name="snyder">''Flattening the Earth: Two Thousand Years of Map Projections'', John P. Snyder, 1993, pp. 258–262, {{ISBN|0-226-76747-7}}.</ref> | The '''van der Grinten projection''' is a compromise ], which means that it is neither ] nor ]. Unlike perspective projections, the van der Grinten projection is an arbitrary geometric construction on the plane. Van der Grinten projects the entire Earth into a circle. It largely preserves the familiar shapes of the ] while modestly reducing Mercator's distortion. Polar regions are subject to extreme distortion. Lines of longitude converge to points at the poles.<ref name="snyder">''Flattening the Earth: Two Thousand Years of Map Projections'', John P. Snyder, 1993, pp. 258–262, {{ISBN|0-226-76747-7}}.</ref> | ||
| ==History== | ==History== | ||
| Line 7: | Line 8: | ||
| == Geometric construction== | == Geometric construction== | ||
| The geometric construction given by van der Grinten can be written algebraically:<ref>, ] Professional Paper 1395, John P. Snyder, 1987, pp. 239–242.</ref> | The geometric construction given by van der Grinten can be written algebraically:<ref> {{Webarchive|url=https://web.archive.org/web/20100701103721/http://pubs.er.usgs.gov/usgspubs/pp/pp1395 |date=2010-07-01 }}, ] Professional Paper 1395, John P. Snyder, 1987, pp. 239–242.</ref> | ||
| <math display="block">\begin{align} | |||
| x &= \pm \pi \frac{A (G - P^2) + |
x &= \pm \pi \frac{A (G - P^2) + \sqrt{A^2 (G - P^2)^2 - (P^2 + A^2) (G^2 - P^2)}}{P^2 + A^2}, \\ | ||
| ^2 (G - P^2)^2 - (P^2 + A^2) (G^2 - P^2)}}{P^2 + A^2}, \\ | |||
| y &= \pm \pi \frac{P Q - A \sqrt{(A^2 + 1) (P^2 + A^2) - Q^2}}{P^2 + A^2}, | y &= \pm \pi \frac{P Q - A \sqrt{(A^2 + 1) (P^2 + A^2) - Q^2}}{P^2 + A^2}, | ||
| \end{align}</math> | \end{align}</math> | ||
| Line 17: | Line 17: | ||
| where ''x'' takes the sign of {{nowrap|''λ'' − ''λ''{{sub|0}}}}, ''y'' takes the sign of ''φ'', and | where ''x'' takes the sign of {{nowrap|''λ'' − ''λ''{{sub|0}}}}, ''y'' takes the sign of ''φ'', and | ||
| <math display="block">\begin{align} | |||
| A &= \frac{1}{2} \left| \frac{\pi}{\lambda - \lambda_0} - \frac{\lambda - \lambda_0}{\pi} \right|, \\ | A &= \frac{1}{2} \left| \frac{\pi}{\lambda - \lambda_0} - \frac{\lambda - \lambda_0}{\pi} \right|, \\ | ||
| G &= \frac{\cos \theta}{\sin \theta + \cos \theta - 1}, \\ | G &= \frac{\cos \theta}{\sin \theta + \cos \theta - 1}, \\ | ||
| Line 27: | Line 27: | ||
| If ''φ'' = 0, then | If ''φ'' = 0, then | ||
| <math display="block">\begin{align} | |||
| x &= (\lambda - \lambda_0), \\ | x &= (\lambda - \lambda_0), \\ | ||
| y &= 0. | y &= 0. | ||
| Line 34: | Line 34: | ||
| Similarly, if ''λ'' = ''λ''{{sub|0}} or ''φ'' = ±{{pi}}/2, then | Similarly, if ''λ'' = ''λ''{{sub|0}} or ''φ'' = ±{{pi}}/2, then | ||
| <math display="block">\begin{align} | |||
| x &= 0, \\ | x &= 0, \\ | ||
| y &= \pm \pi \tan \frac{\theta}{2}. | y &= \pm \pi \tan \frac{\theta}{2}. | ||
| Line 41: | Line 41: | ||
| In all cases, ''φ'' is the ], ''λ'' is the ], and ''λ''{{sub|0}} is the central meridian of the projection. | In all cases, ''φ'' is the ], ''λ'' is the ], and ''λ''{{sub|0}} is the central meridian of the projection. | ||
| == Van der Grinten IV |
== Van der Grinten IV projection == | ||
| The van der Grinten IV projection is a later polyconic map projection developed by Alphons J. van der Grinten. | The van der Grinten IV projection is a later polyconic map projection developed by Alphons J. van der Grinten. | ||
| The central meridian and |
The central meridian and equator are straight lines. All other meridians and parallels are arcs of circles.<ref> | ||
| . | . | ||
| </ref><ref> | </ref><ref> | ||
| Line 64: | Line 64: | ||
| * {{cite web|url=http://www.progonos.com/furuti/MapProj/Normal/ProjOth/projOth.html|title=Projections by Van der Grinten, and variations}} | * {{cite web|url=http://www.progonos.com/furuti/MapProj/Normal/ProjOth/projOth.html|title=Projections by Van der Grinten, and variations}} | ||
| ⚫ | {{Map projections}} | ||
| ==External links== | |||
| ⚫ | {{Map |
||
| ] | ] | ||
Latest revision as of 10:45, 30 December 2023
Compromise map projection
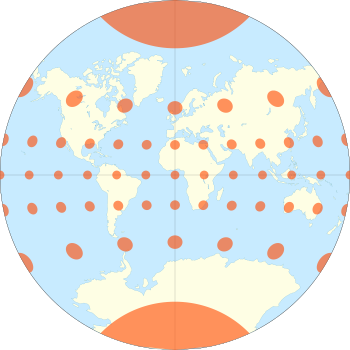
The van der Grinten projection is a compromise map projection, which means that it is neither equal-area nor conformal. Unlike perspective projections, the van der Grinten projection is an arbitrary geometric construction on the plane. Van der Grinten projects the entire Earth into a circle. It largely preserves the familiar shapes of the Mercator projection while modestly reducing Mercator's distortion. Polar regions are subject to extreme distortion. Lines of longitude converge to points at the poles.
History
Alphons J. van der Grinten invented the projection in 1898 and received US patent #751,226 for it and three others in 1904. The National Geographic Society adopted the projection for their reference maps of the world in 1922, raising its visibility and stimulating its adoption elsewhere. In 1988, National Geographic replaced the van der Grinten projection with the Robinson projection.
Geometric construction
The geometric construction given by van der Grinten can be written algebraically:
where x takes the sign of λ − λ0, y takes the sign of φ, and
If φ = 0, then
Similarly, if λ = λ0 or φ = ±π/2, then
In all cases, φ is the latitude, λ is the longitude, and λ0 is the central meridian of the projection.
Van der Grinten IV projection
The van der Grinten IV projection is a later polyconic map projection developed by Alphons J. van der Grinten. The central meridian and equator are straight lines. All other meridians and parallels are arcs of circles.
See also
- List of map projections
- Robinson projection (successor)
References
- ^ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 258–262, ISBN 0-226-76747-7.
- A Bibliography of Map Projections, John P. Snyder and Harry Steward, 1989, p. 94, US Geological Survey Bulletin 1856.
- Map Projections – A Working Manual Archived 2010-07-01 at the Wayback Machine, USGS Professional Paper 1395, John P. Snyder, 1987, pp. 239–242.
- "Van der Grinten IV Projection".
- "An Album of Map Projections". p. 205.
- "van der Grinten IV".
Bibliography
This cartography or mapping term article is a stub. You can help Misplaced Pages by expanding it. |



