| Revision as of 09:43, 29 October 2004 editA1r (talk | contribs)Extended confirmed users787 edits sorting out combat collisions← Previous edit | Latest revision as of 09:34, 29 November 2024 edit undoSlow connect (talk | contribs)6 edits Order of the type of collisions makes more sense now. | ||
| (732 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description|Instance of two or more bodies physically contacting each other within a short period of time}} | |||
| ] | |||
| {{About|physics models|accidents|}} | |||
| ] | |||
| In ], a '''collision''' is any event in which two or more bodies exert ]s on each other in a relatively short time. Although the most common use of the word ''collision'' refers to incidents in which two or more objects collide with great force, the scientific use of the term implies nothing about the magnitude of the force.<ref>{{Cite journal|last=Schmidt|first=Paul W.|date=2019|title=Collision (physics)|url=https://www.accessscience.com/content/collision-physics/149000|journal=Access Science|language=en|doi=10.1036/1097-8542.149000}}</ref> | |||
| == Types of collisions == | |||
| ==Physical collision== | |||
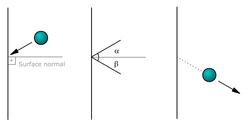
| ] happens when an object hits a plane surface. If the kinetic energy after impact is the same as before impact, it is an elastic collision. If kinetic energy is lost, it is an inelastic collision. The diagram does not show whether the illustrated collision was elastic or inelastic, because no velocities are provided. The most one can say is that the collision was not perfectly inelastic, because in that case the ball would have stuck to the wall.]] | |||
| Collision is short-duration interaction between two bodies or more than two bodies simultaneously causing change in motion of bodies involved due to internal forces acted between them during this. Collisions involve forces (there is a change in ]). The magnitude of the velocity difference just before impact is called the '''closing speed'''. All collisions conserve ]. What distinguishes different types of collisions is whether they also conserve ] of the system before and after the collision. Collisions are of two types: | |||
| #''']''' If all of the total kinetic energy is conserved (i.e. no energy is released as sound, heat, etc.), the collision is said to be ''perfectly elastic''. Such a system is an ] and cannot occur in reality, due to the ]. | |||
| #''']'''. If most or all of the total kinetic energy is lost (] as heat, sound, etc. or absorbed by the objects themselves), the collision is said to be ]; such collisions involve objects coming to a full stop. An example of this is a baseball bat hitting a baseball - the kinetic energy of the bat is transferred to the ball, greatly increasing the ball's velocity. The sound of the bat hitting the ball represents the loss of energy. A "perfectly inelastic" collision (also called a "perfectly plastic" collision) is a ] of inelastic collision in which the two bodies ] after impact. An example of such a collision is a car crash, as cars crumple inward when crashing, rather than bouncing off of each other. This ], for the ] and bystanders should a crash occur - the frame of the car absorbs the energy of the crash instead. | |||
| The degree to which a collision is elastic or inelastic is quantified by the ], a value that generally ranges between zero and one. A perfectly elastic collision has a coefficient of restitution of one; a perfectly inelastic collision has a coefficient of restitution of zero. The line of impact is the line that is collinear to the common normal of the surfaces that are closest or in contact during impact. This is the line along which internal force of collision acts during impact, and Newton's ] is defined only along this line. | |||
| ===Dynamics=== | |||
| Collisions in ] approach perfectly elastic collisions, as do scattering interactions of ] which are deflected by the ]. Some large-scale interactions like the slingshot type gravitational interactions between satellites and planets are almost perfectly elastic. | |||
| In ], '''collision''' means the action of bodies striking or coming together (]ing). Collisions involve forces (there is a change in ]). Collisions can be ], meaning they conserve ] and ], ], meaning they conserve momentum, or totally inelastic (or ]), meaning they conserve momentum and the two objects stick together. | |||
| ==Examples== | |||
| The magnitude of the velocity difference at impact is called the closing speed. | |||
| The field of ] is concerned with moving and colliding objects. | |||
| ===Billiards=== | ===Billiards=== | ||
| {{Anchor|Cue sports}}Collisions play an important role in ]. Because the collisions between ] are nearly ], and the balls roll on a surface that produces low ], their behavior is often used to illustrate ]. After a zero-friction collision of a moving ball with a stationary one of equal mass, the angle between the directions of the two balls is 90 degrees. This is an important fact that professional billiards players take into account,<ref>{{cite web|last=Alciatore |first=David G. |date=January 2006 |url=http://billiards.colostate.edu/technical_proofs/TP_3-1.pdf |archive-url=https://ghostarchive.org/archive/20221009/http://billiards.colostate.edu/technical_proofs/TP_3-1.pdf |archive-date=2022-10-09 |url-status=live |title=TP 3.1 90° rule |access-date=2008-03-08 }}</ref> although it assumes the ball is moving without any impact of friction across the table rather than rolling with friction. | |||
| Consider an elastic collision in two dimensions of any two masses ''m''<sub>1</sub> and ''m''<sub>2</sub>, with respective initial velocities '''u'''<sub>1</sub> and '''u'''<sub>2</sub> where '''u'''<sub>2</sub> = '''0''', and final velocities '''V'''<sub>1</sub> and '''V'''<sub>2</sub>. | |||
| Conservation of momentum gives ''m''<sub>1</sub>'''u'''<sub>1</sub> = ''m''<sub>1</sub>'''V'''<sub>1</sub> + ''m''<sub>2</sub>'''V'''<sub>2</sub>. | |||
| Conservation of energy for an elastic collision gives (1/2)''m''<sub>1</sub>|'''u'''<sub>1</sub>|<sup>2</sup> = (1/2)''m''<sub>1</sub>|'''V'''<sub>1</sub>|<sup>2</sup> + (1/2)''m''<sub>2</sub>|'''V'''<sub>2</sub>|<sup>2</sup>. | |||
| Now consider the case ''m''<sub>1</sub> = ''m''<sub>2</sub>: we obtain '''u'''<sub>1</sub> = '''V'''<sub>1</sub> + '''V'''<sub>2</sub> and |'''u'''<sub>1</sub>|<sup>2</sup> = |'''V'''<sub>1</sub>|<sup>2</sup> + |'''V'''<sub>2</sub>|<sup>2</sup>. | |||
| Taking the ] of each side of the former equation with itself, |'''u'''<sub>1</sub>|<sup>2</sup> = '''u'''<sub>1</sub>•'''u'''<sub>1</sub> = |'''V'''<sub>1</sub>|<sup>2</sup> + |'''V'''<sub>2</sub>|<sup>2</sup> + 2'''V'''<sub>1</sub>•'''V'''<sub>2</sub>. Comparing this with the latter equation gives '''V'''<sub>1</sub>•'''V'''<sub>2</sub> = 0, so they are perpendicular unless '''V'''<sub>1</sub> is the zero vector (which occurs ] the collision is head-on). | |||
| ===Perfect inelastic collision=== | |||
| In ], collisions play an important role. Because the collisions between billiard balls are almost perfectly elastic, and the balls roll on a low-] surface, their predictable behaviour is often used to illustrate ]. | |||
| ] | |||
| ===Traffic=== | |||
| In ] such a collision can be between two ]s, a vehicle and a ], a vehicle and an ], two persons or a person and an object (and more if an ] is involved). It is an ] or even a ]. At ]s sometimes a ] collides with a vehicle or person. Due to the ] and ] of a train it needs a long distance to stop, typically longer than the train ] can see ahead. When a train collides with a car this is more likely to be deadly for the people in the car than for those in the train, because the train has more ] and momentum. | |||
| See also: ] | |||
| ===Attacks by means of a deliberate collision=== | |||
| In a perfect ], i.e., a zero ], the colliding particles ]. It is necessary to consider conservation of momentum: | |||
| Attacks by means of a deliberate collision can be: | |||
| ::<math>m_a \mathbf u_a + m_b \mathbf u_b = \left( m_a + m_b \right) \mathbf v \,</math> | |||
| * with the body: unarmed ], ], ], ], ] | |||
| where '''v''' is the final velocity, which is hence given by | |||
| * striking directly with a ] weapon, such as a ], ] or ] | |||
| ::<math>\mathbf v = \frac{m_a \mathbf u_a + m_b \mathbf u_b}{m_a + m_b}</math> | |||
| The reduction of total kinetic energy is equal to the total kinetic energy before the collision in a ] with respect to the system of two particles, because in such a frame the kinetic energy after the collision is zero. In this frame most of the kinetic energy before the collision is that of the particle with the smaller mass. In another frame, in addition to the reduction of kinetic energy there may be a transfer of kinetic energy from one particle to the other; the fact that this depends on the frame shows how relative this is. | |||
| With time reversed we have the situation of two objects pushed away from each other, e.g. shooting a ], or a ] applying ] (compare the ]). | |||
| ===Animal locomotion=== | |||
| An attacking collision with a distant object can be achieved by throwing or launching a ]. Projectiles can be: | |||
| Collisions of an animal's foot or paw with the underlying substrate are generally termed ground reaction forces. These collisions are inelastic, as kinetic energy is not conserved. An important research topic in ] is quantifying the forces generated during the foot-ground collisions associated with both disabled and non-disabled gait. This quantification typically requires subjects to walk across a ] (sometimes called a "force plate") as well as detailed ] and ] (sometimes termed kinetic) analysis. | |||
| * unpowered, thus depending on momentum transferred from the launcher: | |||
| ** ] | |||
| ** ] | |||
| ** ] | |||
| ** ] | |||
| ** ] | |||
| * powered in flight: | |||
| ** ] | |||
| * guided in flight: | |||
| ** ]. Note that some missile systems such as the ] carry explosives and do not need to achieve a direct collision to be effective. | |||
| === |
===Hypervelocity impacts=== | ||
| ] on comet ].]] | |||
| Hypervelocity is very high ], approximately over 3,000 ] (11,000 km/h, 6,700 mph, 10,000 ft/s, or ] 8.8). In particular, hypervelocity is velocity so high that the strength of materials upon impact is very small compared to ]l stresses.<ref Name="AIAA">{{cite book | |||
| |title= Critical technologies for national defense | |||
| |author= Air Force Institute of Technology | |||
| |year= 1991 | |||
| |publisher= AIAA | |||
| |location= | |||
| |isbn= 1-56347-009-8 | |||
| |page= 287 | |||
| |url= https://books.google.com/books?id=HsEorBWNGWwC&dq=Hypervelocity+3%2C000&pg=PA287}}</ref> Thus, ]s and ]s behave alike under hypervelocity impact. An impact under extreme hypervelocity results in ] of the ] and target. For structural metals, hypervelocity is generally considered to be over 2,500 m/s (5,600 mph, 9,000 km/h, 8,200 ft/s, or Mach 7.3). ] ] are also examples of hypervelocity impacts. | |||
| ==See also== | |||
| *A "collision" applied for construction work, is hitting a ] with a ], etc., and for ] a ]-beater. | |||
| {{colbegin}} | |||
| *In ] a ball is hit with a ], in ]s also a ball or other object is hit, in ] a ball hits a target. | |||
| *] | |||
| *]s slam ]s, ]s, and ]s together. | |||
| *] | |||
| *] for use in ], ], ], physical ] etc. | |||
| *] | |||
| *] are designed to collide for fun. | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] - collisions between ]s | |||
| *] | |||
| {{colend}} | |||
| ==Notes== | |||
| See also: ], ], ] | |||
| {{Reflist}} | |||
| ==References== | |||
| ==Telecommunications== | |||
| * {{cite book | author=Tolman, R. C. | title=The Principles of Statistical Mechanics | url=https://archive.org/details/in.ernet.dli.2015.74301 | publisher=Clarendon Press | year=1938 | location=Oxford}} Reissued (1979) New York: Dover {{ISBN|0-486-63896-0}}. | |||
| ==External links== | |||
| In ], the term '''collision''' has the following meanings: | |||
| * - Oblique inelastic collision between two homogeneous spheres. | |||
| # In a ] ], the situation that occurs when two or more demands are made simultaneously on equipment that can handle only one at any given instant. | |||
| * - One Dimensional Collision Flash Applet. | |||
| # In a ], the situation that occurs when an attempt is made to store simultaneously two different data items at a given ] that can hold only one of the items. | |||
| * - Two Dimensional Collision Flash Applet. | |||
| ] | |||
| ''Source: from ] and from ]'' | |||
| ] | |||
| ] | |||
| See also: ] | |||
Latest revision as of 09:34, 29 November 2024
Instance of two or more bodies physically contacting each other within a short period of time This article is about physics models. For accidents, see Collision (disambiguation).
In physics, a collision is any event in which two or more bodies exert forces on each other in a relatively short time. Although the most common use of the word collision refers to incidents in which two or more objects collide with great force, the scientific use of the term implies nothing about the magnitude of the force.
Types of collisions
Collision is short-duration interaction between two bodies or more than two bodies simultaneously causing change in motion of bodies involved due to internal forces acted between them during this. Collisions involve forces (there is a change in velocity). The magnitude of the velocity difference just before impact is called the closing speed. All collisions conserve momentum. What distinguishes different types of collisions is whether they also conserve kinetic energy of the system before and after the collision. Collisions are of two types:
- Elastic collision If all of the total kinetic energy is conserved (i.e. no energy is released as sound, heat, etc.), the collision is said to be perfectly elastic. Such a system is an idealization and cannot occur in reality, due to the second law of thermodynamics.
- Inelastic collision. If most or all of the total kinetic energy is lost (dissipated as heat, sound, etc. or absorbed by the objects themselves), the collision is said to be inelastic; such collisions involve objects coming to a full stop. An example of this is a baseball bat hitting a baseball - the kinetic energy of the bat is transferred to the ball, greatly increasing the ball's velocity. The sound of the bat hitting the ball represents the loss of energy. A "perfectly inelastic" collision (also called a "perfectly plastic" collision) is a limiting case of inelastic collision in which the two bodies coalesce after impact. An example of such a collision is a car crash, as cars crumple inward when crashing, rather than bouncing off of each other. This is by design, for the safety of the occupants and bystanders should a crash occur - the frame of the car absorbs the energy of the crash instead.
The degree to which a collision is elastic or inelastic is quantified by the coefficient of restitution, a value that generally ranges between zero and one. A perfectly elastic collision has a coefficient of restitution of one; a perfectly inelastic collision has a coefficient of restitution of zero. The line of impact is the line that is collinear to the common normal of the surfaces that are closest or in contact during impact. This is the line along which internal force of collision acts during impact, and Newton's coefficient of restitution is defined only along this line.
Collisions in ideal gases approach perfectly elastic collisions, as do scattering interactions of sub-atomic particles which are deflected by the electromagnetic force. Some large-scale interactions like the slingshot type gravitational interactions between satellites and planets are almost perfectly elastic.
Examples
Billiards
Collisions play an important role in cue sports. Because the collisions between billiard balls are nearly elastic, and the balls roll on a surface that produces low rolling friction, their behavior is often used to illustrate Newton's laws of motion. After a zero-friction collision of a moving ball with a stationary one of equal mass, the angle between the directions of the two balls is 90 degrees. This is an important fact that professional billiards players take into account, although it assumes the ball is moving without any impact of friction across the table rather than rolling with friction. Consider an elastic collision in two dimensions of any two masses m1 and m2, with respective initial velocities u1 and u2 where u2 = 0, and final velocities V1 and V2. Conservation of momentum gives m1u1 = m1V1 + m2V2. Conservation of energy for an elastic collision gives (1/2)m1|u1| = (1/2)m1|V1| + (1/2)m2|V2|. Now consider the case m1 = m2: we obtain u1 = V1 + V2 and |u1| = |V1| + |V2|. Taking the dot product of each side of the former equation with itself, |u1| = u1•u1 = |V1| + |V2| + 2V1•V2. Comparing this with the latter equation gives V1•V2 = 0, so they are perpendicular unless V1 is the zero vector (which occurs if and only if the collision is head-on).
Perfect inelastic collision
In a perfect inelastic collision, i.e., a zero coefficient of restitution, the colliding particles coalesce. It is necessary to consider conservation of momentum:
where v is the final velocity, which is hence given by
The reduction of total kinetic energy is equal to the total kinetic energy before the collision in a center of momentum frame with respect to the system of two particles, because in such a frame the kinetic energy after the collision is zero. In this frame most of the kinetic energy before the collision is that of the particle with the smaller mass. In another frame, in addition to the reduction of kinetic energy there may be a transfer of kinetic energy from one particle to the other; the fact that this depends on the frame shows how relative this is. With time reversed we have the situation of two objects pushed away from each other, e.g. shooting a projectile, or a rocket applying thrust (compare the derivation of the Tsiolkovsky rocket equation).
Animal locomotion
Collisions of an animal's foot or paw with the underlying substrate are generally termed ground reaction forces. These collisions are inelastic, as kinetic energy is not conserved. An important research topic in prosthetics is quantifying the forces generated during the foot-ground collisions associated with both disabled and non-disabled gait. This quantification typically requires subjects to walk across a force platform (sometimes called a "force plate") as well as detailed kinematic and dynamic (sometimes termed kinetic) analysis.
Hypervelocity impacts

Hypervelocity is very high velocity, approximately over 3,000 meters per second (11,000 km/h, 6,700 mph, 10,000 ft/s, or Mach 8.8). In particular, hypervelocity is velocity so high that the strength of materials upon impact is very small compared to inertial stresses. Thus, metals and fluids behave alike under hypervelocity impact. An impact under extreme hypervelocity results in vaporization of the impactor and target. For structural metals, hypervelocity is generally considered to be over 2,500 m/s (5,600 mph, 9,000 km/h, 8,200 ft/s, or Mach 7.3). Meteorite craters are also examples of hypervelocity impacts.
See also
- Ballistic pendulum
- Coefficient of restitution
- Collision detection
- Contact mechanics
- Elastic collision
- Friction
- Impact crater
- Impact event
- Inelastic collision
- Kinetic theory of gases - collisions between molecules
- Projectile
Notes
- Schmidt, Paul W. (2019). "Collision (physics)". Access Science. doi:10.1036/1097-8542.149000.
- Alciatore, David G. (January 2006). "TP 3.1 90° rule" (PDF). Archived (PDF) from the original on 2022-10-09. Retrieved 2008-03-08.
- Air Force Institute of Technology (1991). Critical technologies for national defense. AIAA. p. 287. ISBN 1-56347-009-8.
References
- Tolman, R. C. (1938). The Principles of Statistical Mechanics. Oxford: Clarendon Press. Reissued (1979) New York: Dover ISBN 0-486-63896-0.
External links
- Three Dimensional Collision - Oblique inelastic collision between two homogeneous spheres.
- One Dimensional Collision - One Dimensional Collision Flash Applet.
- Two Dimensional Collision - Two Dimensional Collision Flash Applet.


