| Revision as of 11:07, 4 February 2015 editAnonimski (talk | contribs)Extended confirmed users3,593 editsm clarified← Previous edit | Latest revision as of 22:46, 30 December 2024 edit undoQuondum (talk | contribs)Extended confirmed users36,992 edits fmt | ||
| (784 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Physical constant relating the gravitational force between objects to their mass and distance}} | |||
| {{further|Gravity of Earth|Standard gravity}} | |||
| {{Distinguish|text={{mvar|g}}, the ]}} | |||
| ].]] | |||
| {{Use dmy dates|date=August 2019}} | |||
| {| class="wikitable floatright" | |||
| !scope="col"| Value of {{mvar|G}} | |||
| !scope="col"| Unit | |||
| |- | |||
| | {{physconst|G|unit=no}} | |||
| | ]⋅]{{sup|2}}⋅]{{sup|−2}} | |||
| |- | |||
| | {{val|6.67430|(15)|e=-8}} | |||
| | ]⋅]{{sup|2}}⋅]{{sup|−2}} | |||
| |- | |||
| | {{val|4.3009172706|(3)|e=-3}} | |||
| | ]⋅]{{sup|−1}}⋅(]/]){{sup|2}} | |||
| |} | |||
| ].]] | |||
| The '''gravitational constant''', approximately 6.673×10<sup>−11</sup> N·(m/kg)<sup>2</sup> and denoted by letter {{math|''G''}}, is an ] ] involved in the calculation(s) of ] force between two bodies. It usually appears in ]'s ], and in ]'s ]. It is also known as the '''universal gravitational constant''', '''Newton's constant''', and colloquially as '''Big G'''.<ref>{{cite web |first1=Jens H. |last1=Gundlach |first2=Stephen M. |last2=Merkowitz |title=University of Washington Big G Measurement |work=Astrophysics Science Division |publisher=Goddard Space Flight Center |date=2002-12-23 |url=http://asd.gsfc.nasa.gov/Stephen.Merkowitz/G/Big_G.html |quote=Since Cavendish first measured Newton's Gravitational constant 200 years ago, "Big G" remains one of the most elusive constants in physics.}}</ref> It should not be confused with "small g" ('']''), which is the local gravitational field (equivalent to the free-fall acceleration<ref>Fundamentals of Physics 8ed, Halliday/Resnick/Walker, ISBN 978-0-470-04618-0 p336</ref>), most commonly for that at the Earth's surface. | |||
| The '''gravitational constant''' is an ] ] involved in the calculation of ] effects in ]'s law of universal gravitation and in ]'s ]. It is also known as the '''universal gravitational constant''', the '''Newtonian constant of gravitation''', or the '''Cavendish gravitational constant''',{{efn|"Newtonian constant of gravitation" is the name introduced for ''G'' by Boys (2000). Use of the term by T.E. Stern (1928) was misquoted as "Newton's constant of gravitation" in ''Pure Science Reviewed for Profound and Unsophisticated Students'' (1930), in what is apparently the first use of that term. Use of "Newton's constant" (without specifying "gravitation" or "gravity") is more recent, as "Newton's constant" was also used for the ] in ], but has by now become quite common, e.g. Calmet et al, ''Quantum Black Holes'' (2013), p. 93; P. de Aquino, ''Beyond Standard Model Phenomenology at the LHC'' (2013), p. 3. | |||
| ==Laws and constants== | |||
| According to the law of universal gravitation, the attractive ] (''F'') between two bodies is directly proportional to the product of their ]es (''m''<sub>1</sub> and ''m''<sub>2</sub>), and inversely proportional to the square of the distance, ''r'', (]) between them: | |||
| :<math>F = G\frac{m_1 m_2}{r^2}\ </math> | |||
| The ], ''G'', is the gravitational constant. | |||
| The name "Cavendish gravitational constant", sometimes "Newton–Cavendish gravitational constant", appears to have been common in the 1970s to 1980s, especially in (translations from) Soviet-era Russian literature, e.g. Sagitov (1970 ), ''Soviet Physics: Uspekhi'' 30 (1987), Issues 1–6, p. 342 . | |||
| The gravitational constant is a physical constant that is difficult to measure with high accuracy.<ref name=gillies>{{Citation |author=George T. Gillies |title=The Newtonian gravitational constant: recent measurements and related studies |journal=Reports on Progress in Physics |date=1997 |volume=60 |issue=2 |pages= 151–225 |url=http://www.iop.org/EJ/abstract/0034-4885/60/2/001 |doi=10.1088/0034-4885/60/2/001|bibcode = 1997RPPh...60..151G }}. A lengthy, detailed review. See Figure 1 and Table 2 in particular.</ref> In ] units, the 2010 ]-recommended value of the gravitational constant (with ] in parentheses) is:<ref name="2010 CODATA">P.J. Mohr, B.N. Taylor, and D.B. Newell (2011), "The 2010 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 6.0). This database was developed by J. Baker, M. Douma, and S. Kotochigova. Available: http://physics.nist.gov/constants . National Institute of Standards and Technology, Gaithersburg, MD 20899.</ref> | |||
| "Cavendish constant" and "Cavendish gravitational constant" is also used in Charles W. Misner, Kip S. Thorne, John Archibald Wheeler, "Gravitation", (1973), 1126f. | |||
| :<math> G = 6.67384(80) \times 10^{-11} \ \rm{m}^3 \ \rm{kg}^{-1} \ \rm{s}^{-2} = 6.67384(80) \times 10^{-11} \ {\rm N} \ {\rm m^{2}} \ {\rm kg^{-2}}</math> | |||
| with relative standard uncertainty {{val|1.2|e=-4}}.<ref name="2010 CODATA" /> | |||
| Colloquial use of "Big G", as opposed to "]" for gravitational acceleration dates to the 1960s (R.W. Fairbridge, ''The encyclopedia of atmospheric sciences and astrogeology'', 1967, p. 436; note use of "Big G's" vs. "little g's" as early as the 1940s of the ] ''G''<sub>''μν''</sub> vs. the ] ''g''<sub>''μν''</sub>, ''Scientific, medical, and technical books published in the United States of America: a selected list of titles in print with annotations: supplement of books published 1945–1948'', Committee on American Scientific and Technical Bibliography National Research Council, 1950, p. 26).|name=|group=}} denoted by the capital letter {{math|''G''}}. | |||
| ==Dimensions, units, and magnitude== | |||
| The dimensions assigned to the gravitational constant in the equation above—] cubed, divided by ], and by ] squared (in SI units, meters cubed per ] per second squared)—are those needed to balance the units of measurements in gravitational equations. However, these dimensions have fundamental significance in terms of ]; when expressed in SI units, the gravitational constant is dimensionally and numerically equal to the cube of the ] divided by the product of the ] and the square of ]. | |||
| In Newton's law, it is the proportionality constant connecting the ] between two bodies with the product of their ]es and the ] of their ]. In the ], it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the ]). | |||
| In ], of which ] are a common example, ''G'' and other physical constants such as ''c'' (the ]) may be set equal to 1. | |||
| The measured value of the constant is known with some certainty to four significant digits. In ], its value is approximately <!--{{math|''G''}} = -->{{physconst|G|round=4|unit=N⋅m<sup>2</sup>/kg<sup>2</sup>.}} | |||
| In many secondary school texts, the dimensions of ''G'' are derived from force in order to assist student comprehension: | |||
| :<math> G \approx 6.674 \times 10^{-11} {\rm \ N}\ {\rm (m/kg)^2}.</math> | |||
| The modern notation of Newton's law involving {{math|''G''}} was introduced in the 1890s by ]. The first implicit measurement with an accuracy within about 1% is attributed to ] in a ].{{efn|Cavendish determined the value of ''G'' indirectly, by reporting a value for the ], or the average density of Earth, as {{val|5.448|u=g.cm-3}}.|name=|group=}} | |||
| In ], ''G'' can be written as: | |||
| :<math> G\approx 6.674 \times 10^{-8} {\rm \ cm}^3 \ {\rm g}^{-1} \ {\rm s}^{-2}.</math> | |||
| == Definition == | |||
| ''G'' can also be given as: | |||
| According to Newton's law of universal gravitation, the ] of the attractive ] ({{math|''F''}}) between two bodies each with a spherically symmetric ] distribution is directly proportional to the product of their ]es, {{math|''m''<sub>1</sub>}} and {{math|''m''<sub>2</sub>}}, and inversely proportional to the square of the distance, {{math|''r''}}, directed along the line connecting their ]: | |||
| :<math> G\approx 0.8650 \ {\rm cm}^3 \ {\rm g}^{-1} \ {\rm hr}^{-2}.</math> | |||
| <math display="block">F=G\frac{m_1m_2}{r^2}.</math> | |||
| Given the fact that the period ''P'' of an object in circular orbit around a spherical object obeys | |||
| The ], {{math|''G''}}, in this non-relativistic formulation is the gravitational constant. Colloquially, the gravitational constant is also called "Big G", distinct from "small g" ({{math|''g''}}), which is the local gravitational field of Earth (also referred to as free-fall acceleration).<ref>{{cite web |first1=Jens H. |last1=Gundlach |first2=Stephen M. |last2=Merkowitz |title=University of Washington Big G Measurement |work=Astrophysics Science Division |publisher=Goddard Space Flight Center |date=23 December 2002 |url=http://asd.gsfc.nasa.gov/Stephen.Merkowitz/G/Big_G.html |quote=Since Cavendish first measured Newton's Gravitational constant 200 years ago, 'Big G' remains one of the most elusive constants in physics }}</ref><ref>{{cite book|title=Fundamentals of Physics|edition=8th |last1=Halliday |first1=David |last2=Resnick |first2=Robert |last3=Walker |first3=Jearl |isbn=978-0-470-04618-0 |page=336|title-link=Fundamentals of Physics |date=September 2007 |publisher=John Wiley & Sons, Limited }}</ref> Where <math>M_\oplus</math> is the ] and <math>r_\oplus</math> is the ], the two quantities are related by: | |||
| :<math> GM=3\pi V/P^2</math> | |||
| <math display="block">g = G\frac{M_\oplus}{r_\oplus^2}.</math> | |||
| where ''V'' is the volume inside the radius of the orbit, we see that | |||
| :<math> P^2=\frac{3\pi}{G}\frac{V}{M}\approx 10.896 \ {\rm hr}^2 \ {\rm g}\ {\rm cm}^{-3}\frac{V}{M}.</math> | |||
| This way of expressing ''G'' shows the relationship between the average density of a planet and the period of a satellite orbiting just above its surface. | |||
| The gravitational constant appears in the ] of ],<ref>{{cite book |title=Einstein's General Theory of Relativity: With Modern Applications in Cosmology |edition=illustrated |first1=Øyvind |last1=Grøn |first2=Sigbjorn |last2=Hervik |publisher=Springer Science & Business Media |year=2007 |isbn=978-0-387-69200-5 |page=180 |url=https://books.google.com/books?id=IyJhCHAryuUC&pg=PA180}}</ref><ref name="ein">{{cite journal |last=Einstein |first=Albert |title=The Foundation of the General Theory of Relativity |journal=] |volume=354 |issue=7 |pages=769–822 |year=1916 |url=http://www.alberteinstein.info/gallery/science.html |doi=10.1002/andp.19163540702 |format=] |bibcode=1916AnP...354..769E |archive-url=https://web.archive.org/web/20120206225139/http://www.alberteinstein.info/gallery/gtext3.html |archive-date=6 February 2012}}</ref> | |||
| In some fields of ], where distances are measured in ]s (pc), velocities in kilometers per second (km/s) and masses in ] {{nowrap|(<math>M_\odot</math>)}}, it is useful to express ''G'' as: | |||
| <math display="block">G_{\mu \nu} + \Lambda g_{\mu \nu} = \kappa T_{\mu \nu} \,,</math> | |||
| where {{math|''G''{{sub|''μν''}}}} is the ] (not the gravitational constant despite the use of {{mvar|G}}), {{math|Λ}} is the ], {{mvar|g{{sub|μν}}}} is the ], {{mvar|T{{sub|μν}}}} is the ], and {{math|''κ''}} is the ], a constant originally introduced by ] that is directly related to the Newtonian constant of gravitation:<ref name="ein" /><ref>{{cite book |title= Introduction to General Relativity |url= https://archive.org/details/introductiontoge00adle |url-access= limited |first1=Ronald |last1=Adler |first2=Maurice |last2=Bazin |first3=Menahem |last3=Schiffer |publisher= McGraw-Hill |location= New York |year= 1975 |edition= 2nd |isbn= 978-0-07-000423-8 |page= }}</ref>{{efn|Depending on the choice of definition of the Einstein tensor and of the stress–energy tensor it can alternatively be defined as {{math|1=''κ'' = {{sfrac|8π''G''|''c''<sup>2</sup>}} ≈ {{val|1.866|e=-26|u=m⋅kg<sup>−1</sup>}}}}}} | |||
| <math display="block">\kappa = \frac{8\pi G}{c^4} \approx 2.076\,647(46) \times 10^{-43} \mathrm{~N^{-1}}.</math> | |||
| == Value and uncertainty == | |||
| The gravitational force is extremely weak compared with other ]. For example, the gravitational force between an ] and ] one meter apart is approximately 10<sup>−67</sup> ], whereas the ] between the same two particles is approximately 10<sup>−28</sup> N. Both these forces are weak when compared with the forces we are able to experience directly, but the electromagnetic force in this example is some 39 ] (i.e. 10<sup>39</sup>) greater than the force of gravity—roughly the same ratio as the ] compared to a microgram. | |||
| The gravitational constant is a physical constant that is difficult to measure with high accuracy.<ref name=gillies>{{cite journal|first=George T. |last=Gillies |title=The Newtonian gravitational constant: recent measurements and related studies |journal=Reports on Progress in Physics |date=1997 |volume=60 |issue=2 |pages=151–225 |doi=10.1088/0034-4885/60/2/001|bibcode = 1997RPPh...60..151G |s2cid=250810284 }}. A lengthy, detailed review. See Figure 1 and Table 2 in particular.</ref> This is because the gravitational force is an extremely weak force as compared to other ] at the laboratory scale.{{efn|For example, the gravitational force between an ] and a ] 1 m apart is approximately {{val|e=−67|ul=N}}, whereas the ] between the same two particles is approximately {{val|e=−28|u=N}}. The electromagnetic force in this example is in the order of 10<sup>39</sup> times greater than the force of gravity—roughly the same ratio as the ] to a microgram.|name=|group=}} | |||
| In ] units, the ]-recommended value of the gravitational constant is:{{physconst|G|ref=only}} | |||
| ==History of measurement== | |||
| : <math>G</math> = {{physconst|G|ref=no}} | |||
| The gravitational constant appears in ], but it was not measured until seventy-one years after Newton's death by ] with his ], performed in 1798 (''Philosophical Transactions'' 1798). Cavendish measured ''G'' implicitly, using a ] invented by the geologist Rev. ]. He used a horizontal ] with lead balls whose inertia (in relation to the torsion constant) he could tell by timing the beam's oscillation. Their faint attraction to other balls placed alongside the beam was detectable by the deflection it caused. Cavendish's aim was not actually to measure the gravitational constant, but rather to measure the Earth's density relative to water, through the precise knowledge of the gravitational interaction. In retrospect, the density that Cavendish calculated implies a value for ''G'' of {{nowrap|6.754 × 10<sup>−11</sup> m<sup>3</sup> kg<sup>−1</sup> s<sup>−2</sup>}}.<ref>{{Citation |author=Brush, Stephen G.; Holton, Gerald James |title=Physics, the human adventure: from Copernicus to Einstein and beyond |publisher=Rutgers University Press |location=New Brunswick, N.J |date=2001 |pages= 137 |isbn=0-8135-2908-5 |oclc= |doi= |accessdate=}}</ref> | |||
| The relative standard ] is {{physconst|G|runc=yes|ref=no}}. | |||
| The accuracy of the measured value of ''G'' has increased only modestly since the original Cavendish experiment. ''G'' is quite difficult to measure, as gravity is much weaker than other fundamental forces, and an experimental apparatus cannot be separated from the gravitational influence of other bodies. Furthermore, gravity has no established relation to other fundamental forces, so it does not appear possible to calculate it indirectly from other constants that can be measured more accurately, as is done in some other areas of physics. Published values of ''G'' have varied rather broadly, and some recent measurements of high precision are, in fact, mutually exclusive.<ref name=gillies/><ref name=codata2002>{{Citation |author1=Peter J. Mohr |author2=Barry N. Taylor |title=CODATA recommended values of the fundamental physical constants: 2002 |journal=Reviews of Modern Physics |date=January 2005 |volume=77 |issue=1 | pages= 1–107 |url=http://www.atomwave.org/rmparticle/ao%20refs/aifm%20refs%20sorted%20by%20topic/other%20rmp%20articles/CODATA2005.pdf |format=PDF |accessdate=2006-07-01 |doi=10.1103/RevModPhys.77.1 |bibcode=2005RvMP...77....1M}}. Section Q (pp. 42–47) describes the mutually inconsistent measurement experiments from which the CODATA value for ''G'' was derived.</ref> This led to the 2010 CODATA value by NIST having 20% increased uncertainty than in 2006.<ref>{{Cite journal|url = http://physics.nist.gov/cuu/pdf/RevModPhysCODATA2010.pdf|title = CODATA recommended values of the fundamental physical | |||
| constants: 2010|last = |first = |date = 13 November 2012|journal = Rev Mod Phys, 84|doi = 10.1103/RevModPhys.84.1527|pmid = |access-date = }}</ref> | |||
| === Natural units === | |||
| In the January 2007 issue of '']'', Fixler et al described a new measurement of the gravitational constant by atom inferometry, reporting a value of G = 6.693(34) × 10<sup>−11</sup> m<sup>3</sup>s<sup>2</sup>/kg.<ref>{{Citation |author1=J. B. Fixler |author2=G. T. Foster |author3=J. M. McGuirk |author4=M. A. Kasevich |title=Atom Interferometer Measurement of the Newtonian Constant of Gravity |url=http://www.sciencemag.org/cgi/content/abstract/315/5808/74 |date=2007-01-05 |volume=315 |issue=5808 |pages=74–77 |doi=10.1126/science.1135459 |journal=Science |pmid=17204644 |bibcode=2007Sci...315...74F }}</ref> An improved cold atom measurement by Rosi et al was published in 2014 of ''G''= 6.67191(99) × 10<sup>−11</sup> m<sup>3</sup> kg<sup>−1</sup> s<sup>−2</sup>.<ref>{{cite journal|last1=Schlamminger|first1=Stephan|title=Fundamental constants: A cool way to measure big G|journal=Nature|date=18 June 2014|doi=10.1038/nature13507|bibcode = 2014Natur.510..478S }}</ref> | |||
| Due to its use as a defining<!--sic in cited sources--> constant in some systems of ],<ref>{{cite book |title=The Foundation of Reality: Fundamentality, Space, and Time |author1=David Glick |author2=George Darby |author3=Anna Marmodoro |edition= |publisher=Oxford University Press |year=2020 |isbn=978-0-19-883150-1 |page=99 |url=https://books.google.com/books?id=sqXaDwAAQBAJ}} </ref><ref>{{cite book |title=Relativistic Celestial Mechanics of the Solar System |author1=Sergei Kopeikin |author2=Michael Efroimsky |author3=George Kaplan |edition= |publisher=John Wiley & Sons |year=2011 |isbn=978-3-527-63457-6 |page=820 |url=https://books.google.com/books?id=uN5_DQWSR14C}} </ref> particularly ]s such as ] and ], the value of the gravitational constant will generally have a numeric value of 1 or a value close to it when expressed in terms of those units. Due to the significant uncertainty in the measured value of ''G'' in terms of other known fundamental constants, a similar level of uncertainty will show up in the value of many quantities when expressed in such a unit system. | |||
| <!-- | |||
| Debunked because of the wrong use of the Planck Constant, resulting in wrong dimensional analysis, in the arXiv document. | |||
| === Orbital mechanics === | |||
| See:eprint arXiv:1111.6941 | |||
| {{further|Standard gravitational parameter|orbital mechanics|celestial mechanics|Gaussian gravitational constant|Earth mass|Solar mass}} | |||
| In this study the Newton's gravity constant G has been measured at scale of atoms by the quantum resonance method other than Cavendish's torsion-balance way. The analyzed and experiment model is based on the "hyperfine splitting" of the ground energy state of hydrogen atom. The result is that only in empty space the G is constant, in hydrogen atom (near the distance of ]), the gravitational constant G=6.7192878(13)\times10-11 N\cdotm2/kg2; in vacuum, G=6.6722779(13)\times10-11 N\cdotm2/kg2. This method of experiment has eliminated all sources of possible experimental errors associated with the classical and existed setup, and with a precision better than existing experiments. | |||
| In ], it is convenient to measure distances in ]s (pc), velocities in kilometres per second (km/s) and masses in solar units {{math|''M''{{sub|⊙}}}}. In these units, the gravitational constant is: | |||
| <math display="block"> G \approx 4.3009 \times 10^{-3} {\mathrm{~pc{\cdot}(km/s)^2} \, M_\odot}^{-1} .</math> | |||
| For situations where tides are important, the relevant length scales are ] rather than parsecs. In these units, the gravitational constant is: | |||
| <math display="block"> G \approx 1.908\ 09 \times 10^{5} \mathrm{~(km/s)^2 } \, R_\odot M_\odot^{-1} .</math> | |||
| In ], the period {{math|''P''}} of an object in circular orbit around a spherical object obeys | |||
| <math display="block"> GM=\frac{3\pi V}{P^2} ,</math> | |||
| where {{math|''V''}} is the volume inside the radius of the orbit, and {{math|''M''}} is the total mass of the two objects. It follows that | |||
| : <math> P^2=\frac{3\pi}{G}\frac{V}{M}\approx 10.896 \mathrm{~ h^2 {\cdot} g {\cdot} cm^{-3} \,}\frac{V}{M}.</math> | |||
| This way of expressing {{math|''G''}} shows the relationship between the average density of a planet and the period of a satellite orbiting just above its surface. | |||
| For elliptical orbits, applying ], expressed in units characteristic of ]: | |||
| : <math> G = 4 \pi^2 \mathrm{\ AU^3 {\cdot} yr^{-2}} \ M^{-1} \approx 39.478 \mathrm{\ AU^3 {\cdot} yr^{-2}} \ M_\odot^{-1} ,</math> | |||
| where distance is measured in terms of the ] of Earth's orbit (the ], AU), time in ]s, and mass in the total mass of the orbiting system ({{math|1=''M'' = {{solar mass}} + {{earth mass}} + {{lunar mass|sym=yes}}}}{{efn| | |||
| {{mvar|M}} ≈ {{val|1.000003040433}} {{math|{{solar mass}}}}, so that {{mvar|M}} {{=}} {{math|{{solar mass}}}} can be used for accuracies of five or fewer significant digits.}}). | |||
| The above equation is exact only within the approximation of the Earth's orbit around the Sun as a ] in Newtonian mechanics, the measured quantities contain corrections from the perturbations from other bodies in the solar system and from general relativity. | |||
| From 1964 until 2012, however, it was used as the definition of the astronomical unit and thus held by definition: | |||
| <math display="block"> 1\ \mathrm{AU} = \left( \frac{GM}{4 \pi^2} \mathrm{yr}^2 \right)^{\frac{1}{3}} \approx 1.495\,979 \times 10^{11}\mathrm{~m}.</math> <!--(1.3271244002e+20 * 1.000003040433 * 86400^2 * 365.25636^2)^(1/3) = 1.4959788e+11--> | |||
| Since 2012, the AU is defined as {{val|1.495978707|e=11|u=m}} exactly, and the equation can no longer be taken as holding precisely. | |||
| The quantity {{math|''GM''}}—the product of the gravitational constant and the mass of a given astronomical body such as the Sun or Earth—is known as the ] (also denoted {{math|''μ''}}). The standard gravitational parameter {{math|''GM''}} appears as above in Newton's law of universal gravitation, as well as in formulas for the deflection of light caused by ], in ], and in the formula for ]. | |||
| This quantity gives a convenient simplification of various gravity-related formulas. The product {{math|''GM''}} is known much more accurately than either factor is. | |||
| {| class=wikitable | |||
| |+ Values for ''GM'' | |||
| !scope="col"| Body | |||
| !scope="col"| {{math|1=''μ'' = ''GM''}} | |||
| !scope="col"| Value | |||
| !scope="col"| Relative uncertainty | |||
| |- | |||
| !scope="row"| ] | |||
| | {{math|''G''{{solar mass}}}} | |||
| | {{val|1.32712440018|(8)|e=20|u=m{{sup|3}}⋅s{{sup|−2}}}}<ref name="Astrodynamic Constants">{{cite web | |||
| | title = Astrodynamic Constants | |||
| | date = 27 February 2009 | |||
| | publisher = ]/] | |||
| | url = http://ssd.jpl.nasa.gov/?constants | |||
| | access-date = 27 July 2009 | |||
| }} | |||
| </ref> | |||
| | {{val|6|e=-11}} | |||
| |- | |||
| !scope="row"|] | |||
| | {{math|''G''{{earth mass}}}} | |||
| | {{val|3.986004418|(8)|e=14|u=m{{sup|3}}⋅s{{sup|−2}}}}<ref name="IAU best estimates">{{cite web |title=Geocentric gravitational constant |work=Numerical Standards for Fundamental Astronomy |url=https://iau-a3.gitlab.io/NSFA/NSFA_cbe.html#GME2009 |via=iau-a3.gitlab.io |publisher=IAU Division I Working Group on Numerical Standards for Fundamental Astronomy |access-date=24 June 2021}} Citing | |||
| * {{cite journal|vauthors=Ries JC, Eanes RJ, Shum CK, Watkins MM |s2cid=123322272 |title=Progress in the determination of the gravitational coefficient of the Earth |journal=Geophysical Research Letters | date=20 March 1992 |volume=19 |issue=6 |doi=10.1029/92GL00259 |bibcode=1992GeoRL..19..529R |pages=529–531}}</ref> | |||
| | {{val|2|e=-9}} | |||
| |} | |||
| Calculations in ] can also be carried out using the units of solar masses, ]s and astronomical units rather than standard SI units. For this purpose, the ] was historically in widespread use, {{math|''k'' {{=}} {{val|0.01720209895}} ]s per ]}}, expressing the mean ] of the Sun–Earth system.{{citation needed|date=September 2020}} The use of this constant, and the implied definition of the ] discussed above, has been deprecated by the ] since 2012.{{citation needed|date=September 2020}} | |||
| == History of measurement == | |||
| {{further|Earth mass|Schiehallion experiment|Cavendish experiment}} | |||
| === Early history === | |||
| The existence of the constant is implied in ] as published in the 1680s (although its notation as {{math|''G''}} dates to the 1890s),<ref name=BoysG/> but is not ] in his '']'' where it postulates the ] of gravitation. In the ''Principia'', Newton considered the possibility of measuring gravity's strength by measuring the deflection of a pendulum in the vicinity of a large hill, but thought that the effect would be too small to be measurable.<ref name="Davies">{{cite journal|last=Davies|first=R.D.|title=A Commemoration of Maskelyne at Schiehallion|journal=Quarterly Journal of the Royal Astronomical Society|volume=26|issue=3|pages=289–294|bibcode=1985QJRAS..26..289D|date=1985}}</ref> Nevertheless, he had the opportunity to estimate the order of magnitude of the constant when he surmised that "the mean density of the earth might be five or six times as great as the density of water", which is equivalent to a gravitational constant of the order:<ref>"Sir Isaac Newton thought it probable, that the mean density of the earth might be five or six times as great as the density of water; and we have now found, by experiment, that it is very little less than what he had thought it to be: so much justness was even in the surmises of this wonderful man!" Hutton (1778), p. 783</ref> | |||
| : {{math|''G''}} ≈ {{val|6.7|0.6|e=-11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}} | |||
| A measurement was attempted in 1738 by ] and ] in their "]". Bouguer downplayed the significance of their results in 1740, suggesting that the experiment had at least proved that the Earth could not be a ], as some thinkers of the day, including ], had suggested.<ref name="Poynting_p50-56">{{cite book|last=Poynting|first=J.H.|title=The Earth: its shape, size, weight and spin|publisher=Cambridge|date=1913 |pages=50–56 |url=https://books.google.com/books?id=whA9AAAAIAAJ&pg=PA50}}</ref> | |||
| The ], proposed in 1772 and completed in 1776, was the first successful measurement of the mean density of the Earth, and thus indirectly of the gravitational constant. The result reported by ] (1778) suggested a density of {{val|4.5|u=g/cm3}} ({{sfrac|4|1|2}} times the density of water), about 20% below the modern value.<ref name="Hutton">{{cite journal|last=Hutton|first=C. |date=1778 |title=An Account of the Calculations Made from the Survey and Measures Taken at Schehallien |journal=Philosophical Transactions of the Royal Society |volume=68 |pages=689–788 |doi=10.1098/rstl.1778.0034|doi-access=free }}</ref> This immediately led to estimates on the densities and masses of the ], ] and ], sent by Hutton to ] for inclusion in his planetary tables. As discussed above, establishing the average density of Earth is equivalent to measuring the gravitational constant, given ] and the ] at Earth's surface, by setting<ref name=BoysG>, p.330 In this lecture before the Royal Society, Boys introduces ''G'' and argues for its acceptance. See: | |||
| , p. 4, , p.vi</ref> | |||
| <!--modern values: g=9.80665 ms^-2, Re= 6.3781e+6 m | |||
| 3*g/(4*pi*Re)=3.6706e-7 | |||
| 3.6706e-7/5.448e3=6.7375e-11 | |||
| the "correct" value (for G=6.674e-11) would be 5.500 gcm^-3. | |||
| --> | --> | ||
| <math display="block">G = g\frac{R_\oplus^2}{M_\oplus} = \frac{3g}{4\pi R_\oplus\rho_\oplus}.</math> | |||
| Based on this, Hutton's 1778 result is equivalent to {{nowrap|{{math|''G''}} ≈ {{val|8|e=-11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}}}}. | |||
| ] performed by ] in 1798, to measure G, with the help of a pulley, large balls hung from a frame were rotated into position next to the small balls.]] | |||
| Under the assumption that the physics of ] are universal, analysis of observations of 580 type Ia supernovae has shown that the gravitational constant has varied by less than one part in ten billion per year over the last nine billion years.<ref>{{Citation |author1=J. Mould |author2=S. A. Uddin |title=Constraining a Possible Variation of G with Type Ia Supernovae |url=http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=9198037&fulltextType=RA&fileId=S1323358014000095 |date=2014-04-10 |volume=31 |pages=e015 |doi=10.1017/pasa.2014.9 |journal=Publications of the Astronomical Society of Australia|arxiv = 1402.1534 |bibcode = 2014PASA...31...15M }}</ref> | |||
| The first direct measurement of gravitational attraction between two bodies in the laboratory was performed in 1798, seventy-one years after Newton's death, by Henry Cavendish.<ref>Published in '']'' (1798); reprint: Cavendish, Henry (1798). "Experiments to Determine the Density of the Earth". In MacKenzie, A. S., ''Scientific Memoirs'' Vol. 9: ''The Laws of Gravitation''. American Book Co. (1900), pp. 59–105.</ref> He determined a value for {{math|''G''}} implicitly, using a ] invented by the geologist Rev. ] (1753). He used a horizontal ] with lead balls whose inertia (in relation to the torsion constant) he could tell by timing the beam's oscillation. Their faint attraction to other balls placed alongside the beam was detectable by the deflection it caused. In spite of the experimental design being due to Michell, the experiment is now known as the Cavendish experiment for its first successful execution by Cavendish. | |||
| Cavendish's stated aim was the "weighing of Earth", that is, determining the average density of Earth and the ]. His result, {{nowrap|1={{math|1=''ρ''<sub>🜨</sub>}} = {{val|5.448|(33)|u=g.cm-3}}}}, corresponds to value of {{nowrap|1={{math|1=''G''}} = {{val|6.74|(4)|e=-11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}}}}. It is surprisingly accurate, about 1% above the modern value (comparable to the claimed relative standard uncertainty of 0.6%).<ref>2014 ] value {{val|6.674|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}}.</ref> | |||
| ==The ''GM'' product== | |||
| {{Main|Standard gravitational parameter}} | |||
| === 19th century === | |||
| The quantity ''GM''—the product of the gravitational constant and the mass of a given astronomical body such as the Sun or the Earth—is known as the standard gravitational parameter and is denoted <math>\scriptstyle \mu\!</math>. Depending on the body concerned, it may also be called the geocentric or heliocentric gravitational constant, among other names. | |||
| The accuracy of the measured value of {{math|''G''}} has increased only modestly since the original Cavendish experiment.<ref> | |||
| {{cite book|last1=Brush |first1=Stephen G. |last2=Holton |first2=Gerald James |title=Physics, the human adventure: from Copernicus to Einstein and beyond |url=https://archive.org/details/physicshumanadve00ghol |url-access=limited |publisher=Rutgers University Press |location=New Brunswick, NJ |date=2001 |pages= |isbn=978-0-8135-2908-0 }} | |||
| {{cite journal |first=Jennifer Lauren |last=Lee |title=Big G Redux: Solving the Mystery of a Perplexing Result |date=16 November 2016 |journal=NIST |url=https://www.nist.gov/news-events/news/2016/11/big-g-redux-solving-mystery-perplexing-result}}</ref> {{math|''G''}} is quite difficult to measure because gravity is much weaker than other fundamental forces, and an experimental apparatus cannot be separated from the gravitational influence of other bodies. | |||
| Measurements with pendulums were made by ] (1821, {{val|4.39|u=g/cm3}}), ] (1827, {{val|4.77|u=g/cm3}}), Carlo Ignazio Giulio (1841, {{val|4.95|u=g/cm3}}) and ] (1854, {{val|6.6|u=g/cm3}}).<ref>{{cite book | last = Poynting | first = John Henry | title = The Mean Density of the Earth | publisher = Charles Griffin | date = 1894 | location = London | pages = –24 | url = https://archive.org/details/meandensityeart00poyngoog }}</ref> | |||
| This quantity gives a convenient simplification of various gravity-related formulas. Also, for celestial bodies such as the Earth and the Sun, the value of the product ''GM'' is known much more accurately than each factor independently. Indeed, the limited accuracy available for ''G'' often limits the accuracy of scientific determination of such masses in the first place. | |||
| Cavendish's experiment was first repeated by ] (1838, 1842, 1853), who found a value of {{val|5.5832|(149)|u=g.cm-3}},<ref>F. Reich, ''On the Repetition of the Cavendish Experiments for Determining the mean density of the Earth" ''Philosophical Magazine'' 12: 283–284.''</ref> which is actually worse than Cavendish's result, differing from the modern value by 1.5%. Cornu and Baille (1873), found {{val|5.56|u=g.cm-3}}.<ref>Mackenzie (1899), p. 125.</ref> | |||
| For ], using <math>M_\oplus</math> as the symbol for the mass of the Earth, we have | |||
| : <math> \mu = GM_\oplus = ( 398 600.4418 \pm 0.0008 ) \ \mbox{km}^{3} \ \mbox{s}^{-2}.</math> | |||
| Cavendish's experiment proved to result in more reliable measurements than pendulum experiments of the "Schiehallion" (deflection) type or "Peruvian" (period as a function of altitude) type. Pendulum experiments still continued to be performed, by ] (1883, results between 5.0 and {{val|6.3|u=g/cm3}}) and ] (1880, {{val|5.77|u=g/cm3}}).<ref>A.S. Mackenzie, ''The Laws of Gravitation'' (1899), </ref> | |||
| Calculations in ] can also be carried out using the unit of ] rather than the standard SI unit kilogram. In this case we use the ] ''k'', where | |||
| :<math> {k = 0.01720209895 \ A^{\frac{3}{2}} \ D^{-1} \ S^{-\frac{1}{2}} } \ </math> | |||
| Cavendish's result was first improved upon by ] (1891),<ref>{{cite book |url=https://archive.org/details/meandensityofear00poynuoft |title=The mean density of the earth |last=Poynting |first=John Henry |date=1894 |publisher=London |others=Gerstein - University of Toronto }}</ref> who published a value of {{val|5.49|(3)|u=g.cm-3}}, differing from the modern value by 0.2%, but compatible with the modern value within the cited relative standard uncertainty of 0.55%. In addition to Poynting, measurements were made by ] (1895)<ref>{{cite journal | last=Boys | first=C. V. | title=On the Newtonian Constant of Gravitation | journal=Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences | publisher=The Royal Society | volume=186 | date=1895-01-01 | issn=1364-503X | doi=10.1098/rsta.1895.0001 | bibcode=1895RSPTA.186....1B | pages=1–72| doi-access=free }}</ref> and ]<!--]--> (1897),<ref>Carl Braun, ''Denkschriften der k. Akad. d. Wiss. (Wien), math. u. naturwiss. Classe'', 64 (1897). | |||
| and | |||
| Braun (1897) quoted an optimistic relative standard uncertainty of 0.03%, {{val|6.649|(2)|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}} but his result was significantly worse than the 0.2% feasible at the time.</ref> with compatible results suggesting {{math|''G''}} = {{val|6.66|(1)|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}}. The modern notation involving the constant {{math|''G''}} was introduced by Boys in 1894<ref name=BoysG/> and becomes standard by the end of the 1890s, with values usually cited in the ] system. Richarz and Krigar-Menzel (1898) attempted a repetition of the Cavendish experiment using 100,000 kg of lead for the attracting mass. The precision of their result of {{val|6.683|(11)|e=-11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}} was, however, of the same order of magnitude as the other results at the time.<ref name=Sagitov>Sagitov, M. U., "Current Status of Determinations of the Gravitational Constant and the Mass of the Earth", Soviet Astronomy, Vol. 13 (1970), 712–718, translated from ''Astronomicheskii Zhurnal'' Vol. 46, No. 4 (July–August 1969), 907–915 (table of historical experiments p. 715).</ref> | |||
| :<math>A\!</math> is the ]; | |||
| :<math>D\!</math> is the ]; | |||
| :<math>S\!</math> is the ]. | |||
| ] in ''The Laws of Gravitation'' (1899) reviews the work done in the 19th century.<ref>Mackenzie, A. Stanley, '''', American Book Company (1900 ).</ref> Poynting is the author of the article "Gravitation" in the ] (1911). Here, he cites a value of {{math|''G''}} = {{val|6.66|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}} with a relative uncertainty of 0.2%. | |||
| If instead of mean solar day we use the ] as our time unit, the value of ''ks'' is very close to 2] (''k'' = 6.28315). | |||
| === Modern value === | |||
| The standard gravitational parameter ''GM'' appears as above in Newton's law of universal gravitation, as well as in formulas for the deflection of light caused by ], in ], and in the formula for ]. | |||
| ] (1930) published the value of {{val|6.670|(5)|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}} (relative uncertainty 0.1%),<ref>{{cite journal |first=P. R. |last=Heyl |author-link=Paul R. Heyl |title=A redetermination of the constant of gravitation |journal= Bureau of Standards Journal of Research|volume=5 |issue=6 |year=1930 |pages=1243–1290|doi=10.6028/jres.005.074 |doi-access=free }}<!--Also https://archive.org/details/redeterminationo56124heyl, and a shorter version at https://europepmc.org/articles/PMC1085130--></ref> improved to {{val|6.673|(3)|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}} (relative uncertainty 0.045% = 450 ppm) in 1942.<ref>P. R. Heyl and P. Chrzanowski (1942), cited after Sagitov (1969:715).</ref> | |||
| However, Heyl used the statistical spread as his standard deviation, and he admitted himself that measurements using the same material yielded very similar results while measurements using different materials yielded vastly different results. He spent the next 12 years after his 1930 paper to do more precise measurements, hoping that the composition-dependent effect would go away, but it did not, as he noted in his final paper from the year 1942. | |||
| ==See also== | |||
| Published values of {{mvar|G}} derived from high-precision measurements since the 1950s have remained compatible with Heyl (1930), but within the relative uncertainty of about 0.1% (or 1000 ppm) have varied rather broadly, and it is not entirely clear if the uncertainty has been reduced at all since the 1942 measurement. Some measurements published in the 1980s to 2000s were, in fact, mutually exclusive.<ref name=gillies/><ref name=codata2002>{{cite journal|first1=Peter J. |last1=Mohr |first2=Barry N. |last2=Taylor |title=CODATA recommended values of the fundamental physical constants: 2002 |journal=Reviews of Modern Physics |year=2012 |volume=77 |issue=1 | pages=1–107 |url=http://www.atomwave.org/rmparticle/ao%20refs/aifm%20refs%20sorted%20by%20topic/other%20rmp%20articles/CODATA2005.pdf |access-date=1 July 2006 |doi=10.1103/RevModPhys.77.1 |bibcode=2005RvMP...77....1M |citeseerx=10.1.1.245.4554 |url-status=dead |archive-url=https://web.archive.org/web/20070306174141/http://www.atomwave.org/rmparticle/ao%20refs/aifm%20refs%20sorted%20by%20topic/other%20rmp%20articles/CODATA2005.pdf |archive-date=6 March 2007|arxiv=1203.5425 }} Section Q (pp. 42–47) describes the mutually inconsistent measurement experiments from which the CODATA value for {{mvar|G}} was derived.</ref> Establishing a standard value for {{mvar|G}} with a relative standard uncertainty better than 0.1% has therefore remained rather speculative. | |||
| By 1969, the value recommended by the ] (NIST) was cited with a relative standard uncertainty of 0.046% (460 ppm), lowered to 0.012% (120 ppm) by 1986. But the continued publication of conflicting measurements led NIST to considerably increase the standard uncertainty in the 1998 recommended value, by a factor of 12, to a standard uncertainty of 0.15%, larger than the one given by Heyl (1930). | |||
| The uncertainty was again lowered in 2002 and 2006, but once again raised, by a more conservative 20%, in 2010, matching the relative standard uncertainty of 120 ppm published in 1986.<ref>{{Cite journal|url = http://physics.nist.gov/cuu/pdf/RevModPhysCODATA2010.pdf|title = CODATA recommended values of the fundamental physical constants: 2010|date = 13 November 2012|journal = Reviews of Modern Physics |doi = 10.1103/RevModPhys.84.1527|bibcode=2012RvMP...84.1527M|arxiv = 1203.5425 |volume=84 |issue = 4|pages=1527–1605|last1 = Mohr|first1 = Peter J.|last2 = Taylor|first2 = Barry N.|last3 = Newell|first3 = David B.|s2cid = 103378639|citeseerx = 10.1.1.150.3858}}</ref> For the 2014 update, CODATA reduced the uncertainty to 46 ppm, less than half the 2010 value, and one order of magnitude below the 1969 recommendation. | |||
| The following table shows the NIST recommended values published since 1969: | |||
| ] | |||
| {|class=wikitable | |||
| |+Recommended values for ''G'' | |||
| !scope="col"| Year | |||
| !scope="col"| ''G'' <br />{{bracket|10{{sup|−11}} m{{sup|3}}⋅kg{{sup|−1}}⋅s{{sup|−2}}}} | |||
| ! scope="col"|Relative standard uncertainty | |||
| !scope="col"| Ref. | |||
| |- | |||
| !scope="row"|1969 | |||
| | {{val|6.6732|(31)}} || 460 ppm || <ref>{{cite journal | last1=Taylor | first1=B. N. | last2=Parker | first2=W. H. | last3=Langenberg | first3=D. N. | title=Determination of ''e''/''h'', Using Macroscopic Quantum Phase Coherence in Superconductors: Implications for Quantum Electrodynamics and the Fundamental Physical Constants | journal=Reviews of Modern Physics | publisher=American Physical Society (APS) | volume=41 | issue=3 | date=1969-07-01 | issn=0034-6861 | doi=10.1103/revmodphys.41.375 | bibcode=1969RvMP...41..375T | pages=375–496}}</ref> | |||
| |- | |||
| !scope="row"|1973 | |||
| | {{val|6.6720|(49)}} || 730 ppm || <ref>{{cite journal | last1=Cohen | first1=E. Richard | last2=Taylor | first2=B. N. | title=The 1973 Least-Squares Adjustment of the Fundamental Constants | journal=Journal of Physical and Chemical Reference Data | publisher=AIP Publishing | volume=2 | issue=4 | year=1973 | issn=0047-2689 | doi=10.1063/1.3253130 | bibcode=1973JPCRD...2..663C | pages=663–734| hdl=2027/pst.000029951949 | hdl-access=free }}</ref> | |||
| |- | |||
| !scope="row"|1986 | |||
| | {{val|6.67449|(81)}} || 120 ppm || <ref>{{cite journal | last1=Cohen | first1=E. Richard | last2=Taylor | first2=Barry N. | title=The 1986 adjustment of the fundamental physical constants | journal=Reviews of Modern Physics | publisher=American Physical Society (APS) | volume=59 | issue=4 | date=1987-10-01 | issn=0034-6861 | doi=10.1103/revmodphys.59.1121 | bibcode=1987RvMP...59.1121C | pages=1121–1148}}</ref> | |||
| |- | |||
| !scope="row"|1998 | |||
| | {{val|6.673|(10)}} || 1500 ppm || <ref>{{cite journal | last1=Mohr | first1=Peter J. | last2=Taylor | first2=Barry N. | title=CODATA recommended values of the fundamental physical constants: 1998 | journal=Reviews of Modern Physics | volume=72 | issue=2 | year=2012 | issn=0034-6861 | doi=10.1103/revmodphys.72.351 | bibcode=2000RvMP...72..351M | pages=351–495| arxiv=1203.5425 }}</ref> | |||
| |- | |||
| !scope="row"|2002 | |||
| | {{val|6.6742|(10)}} || 150 ppm || <ref>{{cite journal | last1=Mohr | first1=Peter J. | last2=Taylor | first2=Barry N. | title=CODATA recommended values of the fundamental physical constants: 2002 | journal=Reviews of Modern Physics | volume=77 | issue=1 | year=2012 | issn=0034-6861 | doi=10.1103/revmodphys.77.1 | bibcode=2005RvMP...77....1M | pages=1–107| arxiv=1203.5425 }}</ref> | |||
| |- | |||
| !scope="row"|2006 | |||
| | {{val|6.67428|(67)}} || 100 ppm || <ref>{{cite journal | last1=Mohr | first1=Peter J. | last2=Taylor | first2=Barry N. | last3=Newell | first3=David B. | title=CODATA recommended values of the fundamental physical constants: 2006 | journal=Journal of Physical and Chemical Reference Data | volume=37 | issue=3 | year=2012 | issn=0047-2689 | doi=10.1063/1.2844785 | bibcode=2008JPCRD..37.1187M | pages=1187–1284| arxiv=1203.5425 }}</ref> | |||
| |- | |||
| !scope="row"|2010 | |||
| | {{val|6.67384|(80)}} || 120 ppm || <ref>{{cite journal | last1=Mohr | first1=Peter J. | last2=Taylor | first2=Barry N. | last3=Newell | first3=David B. | title=CODATA Recommended Values of the Fundamental Physical Constants: 2010 | journal=Journal of Physical and Chemical Reference Data | volume=41 | issue=4 | year=2012 | pages=1527–1605 | issn=0047-2689 | doi=10.1063/1.4724320 | bibcode=2012JPCRD..41d3109M | arxiv=1203.5425 }}</ref> | |||
| |- | |||
| !scope="row"|2014 | |||
| | {{val|6.67408|(31)}} || 46 ppm || <ref>{{cite journal | last1=Mohr | first1=Peter J. | last2=Newell | first2=David B. | last3=Taylor | first3=Barry N. | title=CODATA Recommended Values of the Fundamental Physical Constants: 2014 | journal=Journal of Physical and Chemical Reference Data | volume=45 | issue=4 | year=2016 | pages=1527–1605 | issn=0047-2689 | doi=10.1063/1.4954402 | bibcode=2016JPCRD..45d3102M | arxiv=1203.5425 }}</ref> | |||
| |- | |||
| !scope="row"|2018 | |||
| | {{val|6.67430|(15)}} || 22 ppm || <ref>Eite Tiesinga, Peter J. Mohr, David B. Newell, and Barry N. Taylor (2019), "" (Web Version 8.0). Database developed by J. Baker, M. Douma, and ]. National Institute of Standards and Technology, Gaithersburg, MD 20899.</ref> | |||
| |- | |||
| !scope="row"|2022 | |||
| | {{val|6.67430|(15)}} || 22 ppm || <ref>{{citation |author1=Mohr, P. |author2=Tiesinga, E. |author3=Newell, D. |author4=Taylor, B. |date=2024-05-08 |title=Codata Internationally Recommended 2022 Values of the Fundamental Physical Constants |url=https://www.nist.gov/publications/codata-internationally-reconmmended-2022-values-fundamental-physical-constants |access-date=2024-05-15 }}</ref> | |||
| |- | |||
| |} | |||
| In the January 2007 issue of '']'', Fixler et al. described a measurement of the gravitational constant by a new technique, ], reporting a value of {{nowrap|1={{math|''G''}} = {{val|6.693|(34)|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}}}}, 0.28% (2800 ppm) higher than the 2006 CODATA value.<ref>{{cite journal |first1=J. B. |last1=Fixler |first2=G. T. |last2=Foster |first3=J. M. |last3=McGuirk |first4=M. A. |last4=Kasevich |s2cid=6271411 |title=Atom Interferometer Measurement of the Newtonian Constant of Gravity |date=5 January 2007 |volume=315 |issue=5808 |pages=74–77 |doi=10.1126/science.1135459 |journal=Science |pmid=17204644 |bibcode=2007Sci...315...74F }}</ref> An improved cold atom measurement by Rosi et al. was published in 2014 of {{nowrap|1={{math|''G''}} = {{val|6.67191|(99)|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}}}}.<ref> | |||
| {{cite journal | |||
| |last1=Rosi |first1=G. | |||
| |last2=Sorrentino |first2=F. | |||
| |last3=Cacciapuoti |first3=L. | |||
| |last4=Prevedelli |first4=M. | |||
| |last5=Tino |first5=G. M. | |||
| |title=Precision measurement of the Newtonian gravitational constant using cold atoms | |||
| |journal=Nature |volume=510 |issue=7506 |date=26 June 2014 |pages=518–521 | |||
| |url=http://www2.fisica.unlp.edu.ar/materias/FisGral2semestre2/Rosi.pdf |url-status=live | |||
| |archive-url=https://ghostarchive.org/archive/20221009/http://www2.fisica.unlp.edu.ar/materias/FisGral2semestre2/Rosi.pdf | |||
| |archive-date=2022-10-09 | |||
| |doi=10.1038/nature13433 |pmid=24965653 |arxiv=1412.7954 | |||
| |s2cid=4469248 | |||
| |bibcode=2014Natur.510..518R | |||
| }}</ref><ref> | |||
| {{cite journal | |||
| |last1=Schlamminger |first1=Stephan | |||
| |title=Fundamental constants: A cool way to measure big G | |||
| |journal=Nature |volume=510 |issue=7506 |pages=478–480 | |||
| |date=18 June 2014 | |||
| |url=https://www.nature.com/articles/nature13507.pdf | |||
| |archive-url=https://ghostarchive.org/archive/20221009/https://www.nature.com/articles/nature13507.pdf | |||
| |archive-date=2022-10-09 | |||
| |url-status=live | |||
| |doi=10.1038/nature13507 |doi-access=free | |||
| |bibcode=2014Natur.510..478S |pmid=24965646 | |||
| }}</ref> Although much closer to the accepted value (suggesting that the Fixler ''et al.'' measurement was erroneous), this result was 325 ppm below the recommended 2014 CODATA value, with non-overlapping ] intervals. | |||
| <!-- 6.67191(99) vs. 6.67408(31) , a difference of 0.00217(104). Also *barely* not overlapping with the | |||
| 2010 interval, 6.67384(80) (differences 0.00193(127) and 0.00024(86)). | |||
| This doesn't mean anything beyond "2-sigma effect" until the experiment is repeated. | |||
| --> | |||
| As of 2018, efforts to re-evaluate the conflicting results of measurements are underway, coordinated by NIST, notably a repetition of the experiments reported by Quinn et al. (2013).<ref>{{cite journal |author1=C. Rothleitner |author2=S. Schlamminger |title=Invited Review Article: Measurements of the Newtonian constant of gravitation, G |journal=Review of Scientific Instruments |volume=88 |issue=11 |pages=111101 |id=111101 |year=2017 |doi=10.1063/1.4994619 |pmid=29195410 |pmc=8195032 |quote=However, re-evaluating or repeating experiments that have already been performed may provide insights into hidden biases or dark uncertainty. NIST has the unique opportunity to repeat the experiment of Quinn et al. with an almost identical setup. By mid-2018, NIST researchers will publish their results and assign a number as well as an uncertainty to their value.|bibcode=2017RScI...88k1101R |doi-access=free }} Referencing: | |||
| * {{cite journal |author1=T. Quinn |author2=H. Parks |author3=C. Speake |author4=R. Davis |title=Improved determination of G using two methods |journal=Phys. Rev. Lett. |volume=111 |issue=10 |pages=101102 |id=101102 |year=2013 |doi=10.1103/PhysRevLett.111.101102 |pmid=25166649 |bibcode=2013PhRvL.111j1102Q |url=https://www.bipm.org/utils/en/pdf/PhysRevLett.111.101102.pdf |access-date=4 August 2019 |archive-date=4 December 2020 |archive-url=https://web.archive.org/web/20201204172116/https://www.bipm.org/utils/en/pdf/PhysRevLett.111.101102.pdf |url-status=dead }} | |||
| The 2018 experiment was described by {{cite conference |author=C. Rothleitner |url=https://www.bipm.org/cc/CODATA-TGFC/Allowed/2015-02/Rothleitner.pdf |archive-url=https://ghostarchive.org/archive/20221009/https://www.bipm.org/cc/CODATA-TGFC/Allowed/2015-02/Rothleitner.pdf |archive-date=2022-10-09 |url-status=live |title=Newton's Gravitational Constant 'Big' G – A proposed Free-fall Measurement |conference=CODATA Fundamental Constants Meeting, Eltville – 5 February 2015 }}</ref> | |||
| In August 2018, a Chinese research group announced new measurements based on torsion balances, {{val|6.674184|(78)|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}} and {{val|6.674484|(78)|e=−11|u=m<sup>3</sup>⋅kg<sup>−1</sup>⋅s<sup>−2</sup>}} based on two different methods.<ref>{{cite journal|first=Qing |last=Li |s2cid=52121922 |display-authors=etal |title=Measurements of the gravitational constant using two independent methods |journal=Nature |volume=560 |issue=7720 |pages=582–588 |year=2018 |doi=10.1038/s41586-018-0431-5|pmid=30158607 |bibcode=2018Natur.560..582L }}. | |||
| See also: {{cite news|url=https://www.techexplorist.com/physicists-precise-measurement-ever-gravitys-strength/16643/|title=Physicists just made the most precise measurement ever of Gravity's strength|date=31 August 2018|access-date=13 October 2018}}</ref> These are claimed as the most accurate measurements ever made, with standard uncertainties cited as low as 12 ppm. The difference of 2.7{{px1}}] between the two results suggests there could be sources of error unaccounted for. | |||
| == Constancy == | |||
| {{further|Time-variation of fundamental constants}} | |||
| Analysis of observations of 580 ] shows that the gravitational constant has varied by less than one part in ten billion per year over the last nine billion years.<ref>{{cite journal|first1=J. |last1=Mould |first2=S. A. |last2=Uddin |s2cid=119292899 |title=Constraining a Possible Variation of G with Type Ia Supernovae |date=10 April 2014 |volume=31 |pages=e015 |doi=10.1017/pasa.2014.9 |journal=Publications of the Astronomical Society of Australia|arxiv = 1402.1534 |bibcode = 2014PASA...31...15M }}</ref> | |||
| == See also == | |||
| {{Portal|Physics}} | {{Portal|Physics}} | ||
| {{div col|colwidth=18em}} | |||
| {{colbegin||22em}} | |||
| * ] | |||
| *] | |||
| *] | * ] | ||
| * ] | |||
| *] | |||
| * ] | |||
| *] | |||
| *] | * ] | ||
| *] | * ] | ||
| * ] | |||
| *] | |||
| * ] | |||
| {{colend}} | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| {{div col end}} | |||
| == References == | |||
| ; Footnotes : | |||
| {{notelist|45em}} | |||
| ; Citations : | |||
| {{reflist|30em}} | |||
| == |
=== Sources === | ||
| {{ |
{{refbegin}} | ||
| * {{cite book|first=E. Myles |last=Standish. |contribution=Report of the IAU WGAS Sub-group on Numerical Standards |title=Highlights of Astronomy |editor-first=I. |editor-last=Appenzeller |location=Dordrecht |publisher=Kluwer Academic Publishers |date=1995}} ''(Complete report available online: ; . Tables from the report also available: )'' | |||
| * {{cite journal|first1=Jens H. |last1=Gundlach |first2=Stephen M. |last2=Merkowitz |s2cid=15206636 |title=Measurement of Newton's Constant Using a Torsion Balance with Angular Acceleration Feedback |journal=Physical Review Letters |volume=85 |issue=14 |pages=2869–2872 |date=2000 |doi=10.1103/PhysRevLett.85.2869|pmid=11005956 |bibcode=2000PhRvL..85.2869G|arxiv = gr-qc/0006043 |title-link=arXiv:gr-qc/0006043v1 }} | |||
| {{refend}} | |||
| == External links == | |||
| ==References== | |||
| * at the ] | |||
| {{Refbegin}} | |||
| * — additional commentary on measurement problems | |||
| * E. Myles Standish. "Report of the IAU WGAS Sub-group on Numerical Standards". In ''Highlights of Astronomy'', I. Appenzeller, ed. Dordrecht: Kluwer Academic Publishers, 1995. ''(Complete report available online: ; . Tables from the report also available: )'' | |||
| * {{Citation |author1=Jens H. Gundlach |author2=Stephen M. Merkowitz |title=] |journal=Physical Review Letters |volume=85 |issue=14 |pages= 2869–2872 |date=2000 |doi=10.1103/PhysRevLett.85.2869|pmid=11005956 |bibcode=2000PhRvL..85.2869G|arxiv = gr-qc/0006043 }} | |||
| {{Refend}} | |||
| {{Isaac Newton}} | |||
| ==External links== | |||
| {{Scientists whose names are used in physical constants}} | |||
| * at the ] | |||
| {{Authority control}} | |||
| * — additional commentary on measurement problems | |||
| ] | ] | ||
| ] | ] | ||
Latest revision as of 22:46, 30 December 2024
Physical constant relating the gravitational force between objects to their mass and distance Not to be confused with g, the gravity of Earth.
| Value of G | Unit |
|---|---|
| 6.67430(15)×10 | N⋅m⋅kg |
| 6.67430(15)×10 | dyn⋅cm⋅g |
| 4.3009172706(3)×10 | pc⋅M⊙⋅(km/s) |
The gravitational constant is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's theory of general relativity. It is also known as the universal gravitational constant, the Newtonian constant of gravitation, or the Cavendish gravitational constant, denoted by the capital letter G.
In Newton's law, it is the proportionality constant connecting the gravitational force between two bodies with the product of their masses and the inverse square of their distance. In the Einstein field equations, it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the stress–energy tensor).
The measured value of the constant is known with some certainty to four significant digits. In SI units, its value is approximately 6.6743×10 N⋅m/kg.
The modern notation of Newton's law involving G was introduced in the 1890s by C. V. Boys. The first implicit measurement with an accuracy within about 1% is attributed to Henry Cavendish in a 1798 experiment.
Definition
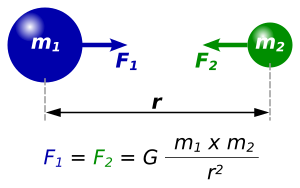
According to Newton's law of universal gravitation, the magnitude of the attractive force (F) between two bodies each with a spherically symmetric density distribution is directly proportional to the product of their masses, m1 and m2, and inversely proportional to the square of the distance, r, directed along the line connecting their centres of mass: The constant of proportionality, G, in this non-relativistic formulation is the gravitational constant. Colloquially, the gravitational constant is also called "Big G", distinct from "small g" (g), which is the local gravitational field of Earth (also referred to as free-fall acceleration). Where is the mass of the Earth and is the radius of the Earth, the two quantities are related by:
The gravitational constant appears in the Einstein field equations of general relativity, where Gμν is the Einstein tensor (not the gravitational constant despite the use of G), Λ is the cosmological constant, gμν is the metric tensor, Tμν is the stress–energy tensor, and κ is the Einstein gravitational constant, a constant originally introduced by Einstein that is directly related to the Newtonian constant of gravitation:
Value and uncertainty
The gravitational constant is a physical constant that is difficult to measure with high accuracy. This is because the gravitational force is an extremely weak force as compared to other fundamental forces at the laboratory scale.
In SI units, the CODATA-recommended value of the gravitational constant is:
- = 6.67430(15)×10 m⋅kg⋅s
The relative standard uncertainty is 2.2×10.
Natural units
Due to its use as a defining constant in some systems of natural units, particularly geometrized unit systems such as Planck units and Stoney units, the value of the gravitational constant will generally have a numeric value of 1 or a value close to it when expressed in terms of those units. Due to the significant uncertainty in the measured value of G in terms of other known fundamental constants, a similar level of uncertainty will show up in the value of many quantities when expressed in such a unit system.
Orbital mechanics
Further information: Standard gravitational parameter, orbital mechanics, celestial mechanics, Gaussian gravitational constant, Earth mass, and Solar massIn astrophysics, it is convenient to measure distances in parsecs (pc), velocities in kilometres per second (km/s) and masses in solar units M⊙. In these units, the gravitational constant is: For situations where tides are important, the relevant length scales are solar radii rather than parsecs. In these units, the gravitational constant is: In orbital mechanics, the period P of an object in circular orbit around a spherical object obeys where V is the volume inside the radius of the orbit, and M is the total mass of the two objects. It follows that
This way of expressing G shows the relationship between the average density of a planet and the period of a satellite orbiting just above its surface.
For elliptical orbits, applying Kepler's 3rd law, expressed in units characteristic of Earth's orbit:
where distance is measured in terms of the semi-major axis of Earth's orbit (the astronomical unit, AU), time in years, and mass in the total mass of the orbiting system (M = M☉ + ME + M☾).
The above equation is exact only within the approximation of the Earth's orbit around the Sun as a two-body problem in Newtonian mechanics, the measured quantities contain corrections from the perturbations from other bodies in the solar system and from general relativity.
From 1964 until 2012, however, it was used as the definition of the astronomical unit and thus held by definition: Since 2012, the AU is defined as 1.495978707×10 m exactly, and the equation can no longer be taken as holding precisely.
The quantity GM—the product of the gravitational constant and the mass of a given astronomical body such as the Sun or Earth—is known as the standard gravitational parameter (also denoted μ). The standard gravitational parameter GM appears as above in Newton's law of universal gravitation, as well as in formulas for the deflection of light caused by gravitational lensing, in Kepler's laws of planetary motion, and in the formula for escape velocity.
This quantity gives a convenient simplification of various gravity-related formulas. The product GM is known much more accurately than either factor is.
| Body | μ = GM | Value | Relative uncertainty |
|---|---|---|---|
| Sun | GM☉ | 1.32712440018(8)×10 m⋅s | 6×10 |
| Earth | GME | 3.986004418(8)×10 m⋅s | 2×10 |
Calculations in celestial mechanics can also be carried out using the units of solar masses, mean solar days and astronomical units rather than standard SI units. For this purpose, the Gaussian gravitational constant was historically in widespread use, k = 0.01720209895 radians per day, expressing the mean angular velocity of the Sun–Earth system. The use of this constant, and the implied definition of the astronomical unit discussed above, has been deprecated by the IAU since 2012.
History of measurement
Further information: Earth mass, Schiehallion experiment, and Cavendish experimentEarly history
The existence of the constant is implied in Newton's law of universal gravitation as published in the 1680s (although its notation as G dates to the 1890s), but is not calculated in his Philosophiæ Naturalis Principia Mathematica where it postulates the inverse-square law of gravitation. In the Principia, Newton considered the possibility of measuring gravity's strength by measuring the deflection of a pendulum in the vicinity of a large hill, but thought that the effect would be too small to be measurable. Nevertheless, he had the opportunity to estimate the order of magnitude of the constant when he surmised that "the mean density of the earth might be five or six times as great as the density of water", which is equivalent to a gravitational constant of the order:
- G ≈ (6.7±0.6)×10 m⋅kg⋅s
A measurement was attempted in 1738 by Pierre Bouguer and Charles Marie de La Condamine in their "Peruvian expedition". Bouguer downplayed the significance of their results in 1740, suggesting that the experiment had at least proved that the Earth could not be a hollow shell, as some thinkers of the day, including Edmond Halley, had suggested.
The Schiehallion experiment, proposed in 1772 and completed in 1776, was the first successful measurement of the mean density of the Earth, and thus indirectly of the gravitational constant. The result reported by Charles Hutton (1778) suggested a density of 4.5 g/cm (4+1/2 times the density of water), about 20% below the modern value. This immediately led to estimates on the densities and masses of the Sun, Moon and planets, sent by Hutton to Jérôme Lalande for inclusion in his planetary tables. As discussed above, establishing the average density of Earth is equivalent to measuring the gravitational constant, given Earth's mean radius and the mean gravitational acceleration at Earth's surface, by setting Based on this, Hutton's 1778 result is equivalent to G ≈ 8×10 m⋅kg⋅s.
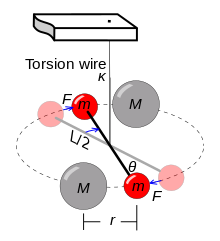
The first direct measurement of gravitational attraction between two bodies in the laboratory was performed in 1798, seventy-one years after Newton's death, by Henry Cavendish. He determined a value for G implicitly, using a torsion balance invented by the geologist Rev. John Michell (1753). He used a horizontal torsion beam with lead balls whose inertia (in relation to the torsion constant) he could tell by timing the beam's oscillation. Their faint attraction to other balls placed alongside the beam was detectable by the deflection it caused. In spite of the experimental design being due to Michell, the experiment is now known as the Cavendish experiment for its first successful execution by Cavendish.
Cavendish's stated aim was the "weighing of Earth", that is, determining the average density of Earth and the Earth's mass. His result, ρ🜨 = 5.448(33) g⋅cm, corresponds to value of G = 6.74(4)×10 m⋅kg⋅s. It is surprisingly accurate, about 1% above the modern value (comparable to the claimed relative standard uncertainty of 0.6%).
19th century
The accuracy of the measured value of G has increased only modestly since the original Cavendish experiment. G is quite difficult to measure because gravity is much weaker than other fundamental forces, and an experimental apparatus cannot be separated from the gravitational influence of other bodies.
Measurements with pendulums were made by Francesco Carlini (1821, 4.39 g/cm), Edward Sabine (1827, 4.77 g/cm), Carlo Ignazio Giulio (1841, 4.95 g/cm) and George Biddell Airy (1854, 6.6 g/cm).
Cavendish's experiment was first repeated by Ferdinand Reich (1838, 1842, 1853), who found a value of 5.5832(149) g⋅cm, which is actually worse than Cavendish's result, differing from the modern value by 1.5%. Cornu and Baille (1873), found 5.56 g⋅cm.
Cavendish's experiment proved to result in more reliable measurements than pendulum experiments of the "Schiehallion" (deflection) type or "Peruvian" (period as a function of altitude) type. Pendulum experiments still continued to be performed, by Robert von Sterneck (1883, results between 5.0 and 6.3 g/cm) and Thomas Corwin Mendenhall (1880, 5.77 g/cm).
Cavendish's result was first improved upon by John Henry Poynting (1891), who published a value of 5.49(3) g⋅cm, differing from the modern value by 0.2%, but compatible with the modern value within the cited relative standard uncertainty of 0.55%. In addition to Poynting, measurements were made by C. V. Boys (1895) and Carl Braun (1897), with compatible results suggesting G = 6.66(1)×10 m⋅kg⋅s. The modern notation involving the constant G was introduced by Boys in 1894 and becomes standard by the end of the 1890s, with values usually cited in the cgs system. Richarz and Krigar-Menzel (1898) attempted a repetition of the Cavendish experiment using 100,000 kg of lead for the attracting mass. The precision of their result of 6.683(11)×10 m⋅kg⋅s was, however, of the same order of magnitude as the other results at the time.
Arthur Stanley Mackenzie in The Laws of Gravitation (1899) reviews the work done in the 19th century. Poynting is the author of the article "Gravitation" in the Encyclopædia Britannica Eleventh Edition (1911). Here, he cites a value of G = 6.66×10 m⋅kg⋅s with a relative uncertainty of 0.2%.
Modern value
Paul R. Heyl (1930) published the value of 6.670(5)×10 m⋅kg⋅s (relative uncertainty 0.1%), improved to 6.673(3)×10 m⋅kg⋅s (relative uncertainty 0.045% = 450 ppm) in 1942.
However, Heyl used the statistical spread as his standard deviation, and he admitted himself that measurements using the same material yielded very similar results while measurements using different materials yielded vastly different results. He spent the next 12 years after his 1930 paper to do more precise measurements, hoping that the composition-dependent effect would go away, but it did not, as he noted in his final paper from the year 1942.
Published values of G derived from high-precision measurements since the 1950s have remained compatible with Heyl (1930), but within the relative uncertainty of about 0.1% (or 1000 ppm) have varied rather broadly, and it is not entirely clear if the uncertainty has been reduced at all since the 1942 measurement. Some measurements published in the 1980s to 2000s were, in fact, mutually exclusive. Establishing a standard value for G with a relative standard uncertainty better than 0.1% has therefore remained rather speculative.
By 1969, the value recommended by the National Institute of Standards and Technology (NIST) was cited with a relative standard uncertainty of 0.046% (460 ppm), lowered to 0.012% (120 ppm) by 1986. But the continued publication of conflicting measurements led NIST to considerably increase the standard uncertainty in the 1998 recommended value, by a factor of 12, to a standard uncertainty of 0.15%, larger than the one given by Heyl (1930).
The uncertainty was again lowered in 2002 and 2006, but once again raised, by a more conservative 20%, in 2010, matching the relative standard uncertainty of 120 ppm published in 1986. For the 2014 update, CODATA reduced the uncertainty to 46 ppm, less than half the 2010 value, and one order of magnitude below the 1969 recommendation.
The following table shows the NIST recommended values published since 1969:

| Year | G [10 m⋅kg⋅s] |
Relative standard uncertainty | Ref. |
|---|---|---|---|
| 1969 | 6.6732(31) | 460 ppm | |
| 1973 | 6.6720(49) | 730 ppm | |
| 1986 | 6.67449(81) | 120 ppm | |
| 1998 | 6.673(10) | 1500 ppm | |
| 2002 | 6.6742(10) | 150 ppm | |
| 2006 | 6.67428(67) | 100 ppm | |
| 2010 | 6.67384(80) | 120 ppm | |
| 2014 | 6.67408(31) | 46 ppm | |
| 2018 | 6.67430(15) | 22 ppm | |
| 2022 | 6.67430(15) | 22 ppm |
In the January 2007 issue of Science, Fixler et al. described a measurement of the gravitational constant by a new technique, atom interferometry, reporting a value of G = 6.693(34)×10 m⋅kg⋅s, 0.28% (2800 ppm) higher than the 2006 CODATA value. An improved cold atom measurement by Rosi et al. was published in 2014 of G = 6.67191(99)×10 m⋅kg⋅s. Although much closer to the accepted value (suggesting that the Fixler et al. measurement was erroneous), this result was 325 ppm below the recommended 2014 CODATA value, with non-overlapping standard uncertainty intervals.
As of 2018, efforts to re-evaluate the conflicting results of measurements are underway, coordinated by NIST, notably a repetition of the experiments reported by Quinn et al. (2013).
In August 2018, a Chinese research group announced new measurements based on torsion balances, 6.674184(78)×10 m⋅kg⋅s and 6.674484(78)×10 m⋅kg⋅s based on two different methods. These are claimed as the most accurate measurements ever made, with standard uncertainties cited as low as 12 ppm. The difference of 2.7 σ between the two results suggests there could be sources of error unaccounted for.
Constancy
Further information: Time-variation of fundamental constantsAnalysis of observations of 580 type Ia supernovae shows that the gravitational constant has varied by less than one part in ten billion per year over the last nine billion years.
See also
- Gravity of Earth
- Standard gravity
- Gaussian gravitational constant
- Orbital mechanics
- Escape velocity
- Gravitational potential
- Gravitational wave
- Strong gravity
- Dirac large numbers hypothesis
- Accelerating expansion of the universe
- Lunar Laser Ranging experiment
- Cosmological constant
References
- Footnotes
- "Newtonian constant of gravitation" is the name introduced for G by Boys (2000). Use of the term by T.E. Stern (1928) was misquoted as "Newton's constant of gravitation" in Pure Science Reviewed for Profound and Unsophisticated Students (1930), in what is apparently the first use of that term. Use of "Newton's constant" (without specifying "gravitation" or "gravity") is more recent, as "Newton's constant" was also used for the heat transfer coefficient in Newton's law of cooling, but has by now become quite common, e.g. Calmet et al, Quantum Black Holes (2013), p. 93; P. de Aquino, Beyond Standard Model Phenomenology at the LHC (2013), p. 3. The name "Cavendish gravitational constant", sometimes "Newton–Cavendish gravitational constant", appears to have been common in the 1970s to 1980s, especially in (translations from) Soviet-era Russian literature, e.g. Sagitov (1970 ), Soviet Physics: Uspekhi 30 (1987), Issues 1–6, p. 342 . "Cavendish constant" and "Cavendish gravitational constant" is also used in Charles W. Misner, Kip S. Thorne, John Archibald Wheeler, "Gravitation", (1973), 1126f. Colloquial use of "Big G", as opposed to "little g" for gravitational acceleration dates to the 1960s (R.W. Fairbridge, The encyclopedia of atmospheric sciences and astrogeology, 1967, p. 436; note use of "Big G's" vs. "little g's" as early as the 1940s of the Einstein tensor Gμν vs. the metric tensor gμν, Scientific, medical, and technical books published in the United States of America: a selected list of titles in print with annotations: supplement of books published 1945–1948, Committee on American Scientific and Technical Bibliography National Research Council, 1950, p. 26).
- Cavendish determined the value of G indirectly, by reporting a value for the Earth's mass, or the average density of Earth, as 5.448 g⋅cm.
- Depending on the choice of definition of the Einstein tensor and of the stress–energy tensor it can alternatively be defined as κ = 8πG/c ≈ 1.866×10 m⋅kg
- For example, the gravitational force between an electron and a proton 1 m apart is approximately 10 N, whereas the electromagnetic force between the same two particles is approximately 10 N. The electromagnetic force in this example is in the order of 10 times greater than the force of gravity—roughly the same ratio as the mass of the Sun to a microgram.
- M ≈ 1.000003040433 M☉, so that M = M☉ can be used for accuracies of five or fewer significant digits.
- Citations
- ^ "2022 CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. NIST. May 2024. Retrieved 18 May 2024.
- Gundlach, Jens H.; Merkowitz, Stephen M. (23 December 2002). "University of Washington Big G Measurement". Astrophysics Science Division. Goddard Space Flight Center.
Since Cavendish first measured Newton's Gravitational constant 200 years ago, 'Big G' remains one of the most elusive constants in physics
- Halliday, David; Resnick, Robert; Walker, Jearl (September 2007). Fundamentals of Physics (8th ed.). John Wiley & Sons, Limited. p. 336. ISBN 978-0-470-04618-0.
- Grøn, Øyvind; Hervik, Sigbjorn (2007). Einstein's General Theory of Relativity: With Modern Applications in Cosmology (illustrated ed.). Springer Science & Business Media. p. 180. ISBN 978-0-387-69200-5.
- ^ Einstein, Albert (1916). "The Foundation of the General Theory of Relativity". Annalen der Physik. 354 (7): 769–822. Bibcode:1916AnP...354..769E. doi:10.1002/andp.19163540702. Archived from the original (PDF) on 6 February 2012.
- Adler, Ronald; Bazin, Maurice; Schiffer, Menahem (1975). Introduction to General Relativity (2nd ed.). New York: McGraw-Hill. p. 345. ISBN 978-0-07-000423-8.
- ^ Gillies, George T. (1997). "The Newtonian gravitational constant: recent measurements and related studies". Reports on Progress in Physics. 60 (2): 151–225. Bibcode:1997RPPh...60..151G. doi:10.1088/0034-4885/60/2/001. S2CID 250810284.. A lengthy, detailed review. See Figure 1 and Table 2 in particular.
- David Glick; George Darby; Anna Marmodoro (2020). The Foundation of Reality: Fundamentality, Space, and Time. Oxford University Press. p. 99. ISBN 978-0-19-883150-1. Extract of page 99
- Sergei Kopeikin; Michael Efroimsky; George Kaplan (2011). Relativistic Celestial Mechanics of the Solar System. John Wiley & Sons. p. 820. ISBN 978-3-527-63457-6. Extract of page 820
- "Astrodynamic Constants". NASA/JPL. 27 February 2009. Retrieved 27 July 2009.
- "Geocentric gravitational constant". Numerical Standards for Fundamental Astronomy. IAU Division I Working Group on Numerical Standards for Fundamental Astronomy. Retrieved 24 June 2021 – via iau-a3.gitlab.io. Citing
- Ries JC, Eanes RJ, Shum CK, Watkins MM (20 March 1992). "Progress in the determination of the gravitational coefficient of the Earth". Geophysical Research Letters. 19 (6): 529–531. Bibcode:1992GeoRL..19..529R. doi:10.1029/92GL00259. S2CID 123322272.
- ^ Boys 1894, p.330 In this lecture before the Royal Society, Boys introduces G and argues for its acceptance. See: Poynting 1894, p. 4, MacKenzie 1900, p.vi
- Davies, R.D. (1985). "A Commemoration of Maskelyne at Schiehallion". Quarterly Journal of the Royal Astronomical Society. 26 (3): 289–294. Bibcode:1985QJRAS..26..289D.
- "Sir Isaac Newton thought it probable, that the mean density of the earth might be five or six times as great as the density of water; and we have now found, by experiment, that it is very little less than what he had thought it to be: so much justness was even in the surmises of this wonderful man!" Hutton (1778), p. 783
- Poynting, J.H. (1913). The Earth: its shape, size, weight and spin. Cambridge. pp. 50–56.
- Hutton, C. (1778). "An Account of the Calculations Made from the Survey and Measures Taken at Schehallien". Philosophical Transactions of the Royal Society. 68: 689–788. doi:10.1098/rstl.1778.0034.
- Published in Philosophical Transactions of the Royal Society (1798); reprint: Cavendish, Henry (1798). "Experiments to Determine the Density of the Earth". In MacKenzie, A. S., Scientific Memoirs Vol. 9: The Laws of Gravitation. American Book Co. (1900), pp. 59–105.
- 2014 CODATA value 6.674×10 m⋅kg⋅s.
- Brush, Stephen G.; Holton, Gerald James (2001). Physics, the human adventure: from Copernicus to Einstein and beyond. New Brunswick, NJ: Rutgers University Press. pp. 137. ISBN 978-0-8135-2908-0. Lee, Jennifer Lauren (16 November 2016). "Big G Redux: Solving the Mystery of a Perplexing Result". NIST.
- Poynting, John Henry (1894). The Mean Density of the Earth. London: Charles Griffin. pp. 22–24.
- F. Reich, On the Repetition of the Cavendish Experiments for Determining the mean density of the Earth" Philosophical Magazine 12: 283–284.
- Mackenzie (1899), p. 125.
- A.S. Mackenzie, The Laws of Gravitation (1899), 127f.
- Poynting, John Henry (1894). The mean density of the earth. Gerstein - University of Toronto. London.
- Boys, C. V. (1 January 1895). "On the Newtonian Constant of Gravitation". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 186. The Royal Society: 1–72. Bibcode:1895RSPTA.186....1B. doi:10.1098/rsta.1895.0001. ISSN 1364-503X.
- Carl Braun, Denkschriften der k. Akad. d. Wiss. (Wien), math. u. naturwiss. Classe, 64 (1897). Braun (1897) quoted an optimistic relative standard uncertainty of 0.03%, 6.649(2)×10 m⋅kg⋅s but his result was significantly worse than the 0.2% feasible at the time.
- Sagitov, M. U., "Current Status of Determinations of the Gravitational Constant and the Mass of the Earth", Soviet Astronomy, Vol. 13 (1970), 712–718, translated from Astronomicheskii Zhurnal Vol. 46, No. 4 (July–August 1969), 907–915 (table of historical experiments p. 715).
- Mackenzie, A. Stanley, The laws of gravitation; memoirs by Newton, Bouguer and Cavendish, together with abstracts of other important memoirs, American Book Company (1900 ).
- Heyl, P. R. (1930). "A redetermination of the constant of gravitation". Bureau of Standards Journal of Research. 5 (6): 1243–1290. doi:10.6028/jres.005.074.
- P. R. Heyl and P. Chrzanowski (1942), cited after Sagitov (1969:715).
- Mohr, Peter J.; Taylor, Barry N. (2012). "CODATA recommended values of the fundamental physical constants: 2002" (PDF). Reviews of Modern Physics. 77 (1): 1–107. arXiv:1203.5425. Bibcode:2005RvMP...77....1M. CiteSeerX 10.1.1.245.4554. doi:10.1103/RevModPhys.77.1. Archived from the original (PDF) on 6 March 2007. Retrieved 1 July 2006. Section Q (pp. 42–47) describes the mutually inconsistent measurement experiments from which the CODATA value for G was derived.
- Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (13 November 2012). "CODATA recommended values of the fundamental physical constants: 2010" (PDF). Reviews of Modern Physics. 84 (4): 1527–1605. arXiv:1203.5425. Bibcode:2012RvMP...84.1527M. CiteSeerX 10.1.1.150.3858. doi:10.1103/RevModPhys.84.1527. S2CID 103378639.
- Taylor, B. N.; Parker, W. H.; Langenberg, D. N. (1 July 1969). "Determination of e/h, Using Macroscopic Quantum Phase Coherence in Superconductors: Implications for Quantum Electrodynamics and the Fundamental Physical Constants". Reviews of Modern Physics. 41 (3). American Physical Society (APS): 375–496. Bibcode:1969RvMP...41..375T. doi:10.1103/revmodphys.41.375. ISSN 0034-6861.
- Cohen, E. Richard; Taylor, B. N. (1973). "The 1973 Least-Squares Adjustment of the Fundamental Constants". Journal of Physical and Chemical Reference Data. 2 (4). AIP Publishing: 663–734. Bibcode:1973JPCRD...2..663C. doi:10.1063/1.3253130. hdl:2027/pst.000029951949. ISSN 0047-2689.
- Cohen, E. Richard; Taylor, Barry N. (1 October 1987). "The 1986 adjustment of the fundamental physical constants". Reviews of Modern Physics. 59 (4). American Physical Society (APS): 1121–1148. Bibcode:1987RvMP...59.1121C. doi:10.1103/revmodphys.59.1121. ISSN 0034-6861.
- Mohr, Peter J.; Taylor, Barry N. (2012). "CODATA recommended values of the fundamental physical constants: 1998". Reviews of Modern Physics. 72 (2): 351–495. arXiv:1203.5425. Bibcode:2000RvMP...72..351M. doi:10.1103/revmodphys.72.351. ISSN 0034-6861.
- Mohr, Peter J.; Taylor, Barry N. (2012). "CODATA recommended values of the fundamental physical constants: 2002". Reviews of Modern Physics. 77 (1): 1–107. arXiv:1203.5425. Bibcode:2005RvMP...77....1M. doi:10.1103/revmodphys.77.1. ISSN 0034-6861.
- Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). "CODATA recommended values of the fundamental physical constants: 2006". Journal of Physical and Chemical Reference Data. 37 (3): 1187–1284. arXiv:1203.5425. Bibcode:2008JPCRD..37.1187M. doi:10.1063/1.2844785. ISSN 0047-2689.
- Mohr, Peter J.; Taylor, Barry N.; Newell, David B. (2012). "CODATA Recommended Values of the Fundamental Physical Constants: 2010". Journal of Physical and Chemical Reference Data. 41 (4): 1527–1605. arXiv:1203.5425. Bibcode:2012JPCRD..41d3109M. doi:10.1063/1.4724320. ISSN 0047-2689.
- Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (2016). "CODATA Recommended Values of the Fundamental Physical Constants: 2014". Journal of Physical and Chemical Reference Data. 45 (4): 1527–1605. arXiv:1203.5425. Bibcode:2016JPCRD..45d3102M. doi:10.1063/1.4954402. ISSN 0047-2689.
- Eite Tiesinga, Peter J. Mohr, David B. Newell, and Barry N. Taylor (2019), "The 2018 CODATA Recommended Values of the Fundamental Physical Constants" (Web Version 8.0). Database developed by J. Baker, M. Douma, and S. Kotochigova. National Institute of Standards and Technology, Gaithersburg, MD 20899.
- Mohr, P.; Tiesinga, E.; Newell, D.; Taylor, B. (8 May 2024), Codata Internationally Recommended 2022 Values of the Fundamental Physical Constants, retrieved 15 May 2024
- Fixler, J. B.; Foster, G. T.; McGuirk, J. M.; Kasevich, M. A. (5 January 2007). "Atom Interferometer Measurement of the Newtonian Constant of Gravity". Science. 315 (5808): 74–77. Bibcode:2007Sci...315...74F. doi:10.1126/science.1135459. PMID 17204644. S2CID 6271411.
- Rosi, G.; Sorrentino, F.; Cacciapuoti, L.; Prevedelli, M.; Tino, G. M. (26 June 2014). "Precision measurement of the Newtonian gravitational constant using cold atoms" (PDF). Nature. 510 (7506): 518–521. arXiv:1412.7954. Bibcode:2014Natur.510..518R. doi:10.1038/nature13433. PMID 24965653. S2CID 4469248. Archived (PDF) from the original on 9 October 2022.
- Schlamminger, Stephan (18 June 2014). "Fundamental constants: A cool way to measure big G" (PDF). Nature. 510 (7506): 478–480. Bibcode:2014Natur.510..478S. doi:10.1038/nature13507. PMID 24965646. Archived (PDF) from the original on 9 October 2022.
- C. Rothleitner; S. Schlamminger (2017). "Invited Review Article: Measurements of the Newtonian constant of gravitation, G". Review of Scientific Instruments. 88 (11): 111101. Bibcode:2017RScI...88k1101R. doi:10.1063/1.4994619. PMC 8195032. PMID 29195410. 111101.
However, re-evaluating or repeating experiments that have already been performed may provide insights into hidden biases or dark uncertainty. NIST has the unique opportunity to repeat the experiment of Quinn et al. with an almost identical setup. By mid-2018, NIST researchers will publish their results and assign a number as well as an uncertainty to their value.
Referencing:- T. Quinn; H. Parks; C. Speake; R. Davis (2013). "Improved determination of G using two methods" (PDF). Phys. Rev. Lett. 111 (10): 101102. Bibcode:2013PhRvL.111j1102Q. doi:10.1103/PhysRevLett.111.101102. PMID 25166649. 101102. Archived from the original (PDF) on 4 December 2020. Retrieved 4 August 2019.
- Li, Qing; et al. (2018). "Measurements of the gravitational constant using two independent methods". Nature. 560 (7720): 582–588. Bibcode:2018Natur.560..582L. doi:10.1038/s41586-018-0431-5. PMID 30158607. S2CID 52121922.. See also: "Physicists just made the most precise measurement ever of Gravity's strength". 31 August 2018. Retrieved 13 October 2018.
- Mould, J.; Uddin, S. A. (10 April 2014). "Constraining a Possible Variation of G with Type Ia Supernovae". Publications of the Astronomical Society of Australia. 31: e015. arXiv:1402.1534. Bibcode:2014PASA...31...15M. doi:10.1017/pasa.2014.9. S2CID 119292899.
Sources
- Standish., E. Myles (1995). "Report of the IAU WGAS Sub-group on Numerical Standards". In Appenzeller, I. (ed.). Highlights of Astronomy. Dordrecht: Kluwer Academic Publishers. (Complete report available online: PostScript; PDF. Tables from the report also available: Astrodynamic Constants and Parameters)
- Gundlach, Jens H.; Merkowitz, Stephen M. (2000). "Measurement of Newton's Constant Using a Torsion Balance with Angular Acceleration Feedback". Physical Review Letters. 85 (14): 2869–2872. arXiv:gr-qc/0006043. Bibcode:2000PhRvL..85.2869G. doi:10.1103/PhysRevLett.85.2869. PMID 11005956. S2CID 15206636.
External links
- Newtonian constant of gravitation G at the National Institute of Standards and Technology References on Constants, Units, and Uncertainty
- The Controversy over Newton's Gravitational Constant — additional commentary on measurement problems
 The
The  is the
is the  is the
is the 
 where Gμν is the
where Gμν is the 
 = 6.67430(15)×10 m⋅kg⋅s
= 6.67430(15)×10 m⋅kg⋅s For situations where tides are important, the relevant length scales are
For situations where tides are important, the relevant length scales are  In
In  where V is the volume inside the radius of the orbit, and M is the total mass of the two objects. It follows that
where V is the volume inside the radius of the orbit, and M is the total mass of the two objects. It follows that


 Since 2012, the AU is defined as 1.495978707×10 m exactly, and the equation can no longer be taken as holding precisely.
Since 2012, the AU is defined as 1.495978707×10 m exactly, and the equation can no longer be taken as holding precisely.
 Based on this, Hutton's 1778 result is equivalent to G ≈ 8×10 m⋅kg⋅s.
Based on this, Hutton's 1778 result is equivalent to G ≈ 8×10 m⋅kg⋅s.