| Revision as of 15:20, 19 June 2008 editMattbuck (talk | contribs)Autopatrolled, Extended confirmed users, Pending changes reviewers, Rollbackers22,201 edits →Meaning of Exponent In Trigonometric Expressions?: comment← Previous edit | Revision as of 15:27, 19 June 2008 edit undoTango (talk | contribs)Pending changes reviewers, Rollbackers19,387 edits →Meaning of Exponent In Trigonometric Expressions?Next edit → | ||
| Line 234: | Line 234: | ||
| :::Be careful though, as <math>\sin^{-1}(x) \neq \dfrac{1}{\sin (x)}</math>, but is instead equal to <math>\arcsin (x)</math>. -'']'' <small>(])</small> 15:20, 19 June 2008 (UTC) | :::Be careful though, as <math>\sin^{-1}(x) \neq \dfrac{1}{\sin (x)}</math>, but is instead equal to <math>\arcsin (x)</math>. -'']'' <small>(])</small> 15:20, 19 June 2008 (UTC) | ||
| ::::And if you see <math>\sin^{-2}(x)</math>, it's best just to run away and hide! --] (]) 15:27, 19 June 2008 (UTC) | |||
| == savant mathématicien == | == savant mathématicien == | ||
Revision as of 15:27, 19 June 2008
Welcome to the mathematics sectionof the Misplaced Pages reference desk. skip to bottom Select a section: Shortcut Want a faster answer?
Main page: Help searching Misplaced Pages
How can I get my question answered?
- Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
- Post your question to only one section, providing a short header that gives the topic of your question.
- Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
- Don't post personal contact information – it will be removed. Any answers will be provided here.
- Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
- Note:
- We don't answer (and may remove) questions that require medical diagnosis or legal advice.
- We don't answer requests for opinions, predictions or debate.
- We don't do your homework for you, though we'll help you past the stuck point.
- We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.
How do I answer a question?
Main page: Misplaced Pages:Reference desk/Guidelines
- The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.
June 13
Mandelbrot set
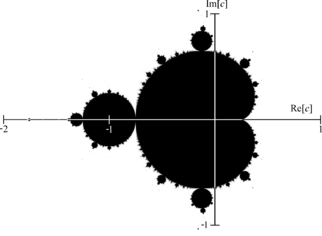
I'm looking at only real values of c i.e. along the horizontal axis of the graph. Black and white describe whether this iteration goes to infinity or not:
xn+1 = xn + c
Consider the points (1,0) and (-1,0). In the iteration they are squared.
1 = 1
-1 = 1
Since squaring these real values gives the same result, how is it that one point is in the Mandelbrot set and the other isn't ? Cuddlyable3 (talk) 17:30, 13 June 2008 (UTC)
- You seem to be confusing the roles of c and . The Mandelbrot set is the set of values c for which the sequence doesn't diverge, starting from x0=0. For c = 1, the sequence starts 0,1,2,5,26..., which diverges, but for c = -1 it starts 0,-1,0,-1,..., which does not. What you are thinking of is more like a Julia set. --169.230.94.28 (talk) 17:50, 13 June 2008 (UTC)
- Um, technically, the sequence 0,-1,0,-1,... does diverge, which simply means that it does not converge. I think the criterion you want is that c is in the set if the corresponding sequence is bounded. --Trovatore (talk) 19:00, 13 June 2008 (UTC)
- Thank you for clarifying this. My error was supposing x0 to start as c. The intro to Mandelbrot set does not state x0=0, it only implies this by examples. Cuddlyable3 (talk) 18:17, 13 June 2008 (UTC)
- Actually it does, but in very technical terminology. It talks about the "orbit of 0", which means all the numbers you can get to by starting at zero and applying the formula. It could be explained much better, I'll have a go now. --Tango (talk) 18:57, 13 June 2008 (UTC)
- It does not matter: if then so you could think of starting from (as long as you do it consistently). – b_jonas 15:27, 14 June 2008 (UTC)
- You don't even need to be consistent. If a sequence is bounded, the same sequence with the index offset by 1 is still bounded, and that's all that's required to be in the Mandelbrot set. If you want to do it with pretty colours showing how quickly it goes to infinity, then you need to be consistent. --Tango (talk) 16:22, 14 June 2008 (UTC)
Second Order Differntial Equation
Can anyone offer advice on how to go about solving the equation;
thanks. Philc 0780 20:21, 13 June 2008 (UTC)
- Well, I can say that y=0 is a nice solution to it... But otherwise, not offhand. -mattbuck (Talk) 21:59, 13 June 2008 (UTC)
- Mathematica is able to "solve" it, but I don't know if the solution would be at all useful. It looks quite complicated. Mathematica gives two solutions that are almost the same. Both are given in terms of the inverse function x(y). Here is one of them:
- You can set the constants C and C to anything. I doubt that this is very helpful. Oded (talk) 22:51, 13 June 2008 (UTC)
- Mathematica is able to "solve" it, but I don't know if the solution would be at all useful. It looks quite complicated. Mathematica gives two solutions that are almost the same. Both are given in terms of the inverse function x(y). Here is one of them:
- Express . You get a separable equation:
- — Pt (T) 13:49, 14 June 2008 (UTC)
- Nice! I guess that's basically how Mathematica does it. Is the trick standard? Oded (talk) 21:36, 15 June 2008 (UTC)
- — Pt (T) 13:49, 14 June 2008 (UTC)
- Express . You get a separable equation:
- I think it is standard. I learnt it once from a differential calculus textbook, but I don't have it around right now, so can't look it up. — Pt (T) 23:12, 15 June 2008 (UTC)
- An example of lecture notes describing briefly the technique is , look at the last section. — Pt (T) 23:25, 15 June 2008 (UTC)
- It is a reasonably common technique to use in second order ODEs that do not include the independent variable (i.e. of the form f(y, y', y'') = 0). The substitution may also be written as . Confusing Manifestation(Say hi!) 00:28, 16 June 2008 (UTC)
June 14
Shift registers
Would someone like to check whether Fibonacci registers with taps in this table for 12 13 14 16 or 19 bits are maximal as claimed? (Question posed at Talk:Linear feedback shift register) Cuddlyable3 (talk) 12:15, 14 June 2008 (UTC)
I need more help translating currency
What is the difference of L500,000.00UGSP and L450,000.00GSP ? —Preceding unsigned comment added by 151.213.231.202 (talk) 15:44, 14 June 2008 (UTC)
- I don't recognise those abbreviations. What does the L stand for, and what do UGSP and GSP stand for? If you aren't sure either, could you describe the context you found these numbers in? --Tango (talk) 16:18, 14 June 2008 (UTC)
50,000 L ? Lira? GSP more context needed please...87.102.86.73 (talk) 19:41, 14 June 2008 (UTC)
hypergeometric series??
I mentioned in an earlier question a differential equation I was having problems with..
I found the solution to this in terms of an infinte polynomial in x where the coefficients were:
an+2(n+2)(n+3)=pan+1+qan
p and q are any number in general. (In general I'm aware of solutions such as e , e(1-x/n), and further solutions such as ef(x) where f(x) is a finite polynomial..)
The nearest thing I could find to this was hypergeometric series - except those seem to only have an+1 and an terms. Is there an article on such things? Can anyone give links to anything that deals with the resultant polynomials? To be more specific - it looks like I should be finding a way to evaluate the polynomial as x tends to infinty in the general case.. —Preceding unsigned comment added by 87.102.86.73 (talk) 19:32, 14 June 2008 (UTC)
June 15
solution of a Diophantine equation
Given integer n, what are solutions in integers x and y of the Diophantine equation x^2-y^2=n? Bubba73 (talk), 06:11, 15 June 2008 (UTC)
x = √n*sec(t) y = √n*tan(t)
for some parameter t. —Preceding unsigned comment added by 124.191.114.87 (talk) 06:45, 15 June 2008 (UTC)
- x−y=(x+y)(x−y). So factor n=ab and chose x=(a+b)/2, y=(a−b)/2. If n is odd then x and y are integers. If n is even but not divisible by 4 then a+b and a−b are odd and there are no integer solutions. If n is divisible by 4 then chose a and b even. Bo Jacoby (talk) 08:12, 15 June 2008 (UTC).
- Thanks, I had thought of factoring n, but I didn't know if that was the best way. I need all solutions, so that will do it. Bubba73 (talk), 14:28, 15 June 2008 (UTC)
question about inequalities
Hi Why does the inequality sigh change when both sides are multiplied or divided by a negative number?Does this happen with equations? —Preceding unsigned comment added by Lighteyes22003 (talk • contribs) 08:37, 15 June 2008 (UTC)
- Is the "inequality sigh" the sound you make when confronted with an inequality ? :-) StuRat (talk) 05:08, 16 June 2008 (UTC)
- Hi, your questions sound very much like homework, and we will not do your homework for you. We may give hints if you have at least shown you have tried to do it. I suggest you look at the article on inequality. -mattbuck (Talk) 14:13, 15 June 2008 (UTC)
- The questions don't sound like homework to me, but rather requests for clarification of topics that were not clearly explained in the OP's class. They are very difficult to answer without knowing more about the OP's background. -- Meni Rosenfeld (talk) 14:18, 15 June 2008 (UTC)
- Look what happens with this simple inequality: . You see that multiplying both sides by minus 2 gives . That demonstrates the inequality sign turning around. Equations don't contain inequality signs, instead they have an equals sign that doesn't change, as long as you multiply or divide both sides by the same (any) number.Cuddlyable3 (talk) 14:55, 15 June 2008 (UTC)
- The questions don't sound like homework to me, but rather requests for clarification of topics that were not clearly explained in the OP's class. They are very difficult to answer without knowing more about the OP's background. -- Meni Rosenfeld (talk) 14:18, 15 June 2008 (UTC)
- (This doesn't sound like homework to me, it's a general question.) When you multiply by a negative number, the number line is basically flipped over, it's reflected about zero. This reverses all the inequalities. For example 1 < 2, but -1 > -2. It's pretty obvious that this works with numbers, but it works in exactly the same way with more complicated expressions, since once you evaluate them at a particular point, they are just numbers. Diving works in the same way as multiplying, since it's just multiplying by one over the number. Does that help at all? --Tango (talk) 14:58, 15 June 2008 (UTC)
- Oh, and no, it doesn't happen with equations. You can't flip an equals sign - if two things are equal, you can do anything you like to them and as long as you do the same thing to both, they will still be equal. --Tango (talk) 14:59, 15 June 2008 (UTC)
- This doesn't look anything like homework to me either. The "flipping the inequality sign" bit also applies to taking a negative root. Thus X > 4 has solutions of X > 2 and X < -2. With some practice you should have flippin' inequality signs mastered in no time. StuRat (talk) 05:12, 16 June 2008 (UTC)
Inequality
How do you know if a value is a solution to an inequality?How is this difference from determining if a value is a solution to an equation?Lets say you replace the equal sigh with the inequality sign,is there ever a time when you have the same value solution for both an inequality and the equation? —Preceding unsigned comment added by Lighteyes22003 (talk • contribs) 08:44, 15 June 2008 (UTC)
- Hi, your questions sound very much like homework, and we will not do your homework for you. We may give hints if you have at least shown you have tried to do it. I suggest you look at the article on inequality. -mattbuck (Talk) 14:13, 15 June 2008 (UTC)
- See my comment above. -- Meni Rosenfeld (talk) 14:19, 15 June 2008 (UTC)
- Put the value you think is the solution back into the equation or inequality concerned and see whether it works. For example, is an equation and its solution is . You know this solution is right because times indeed equals 12. Note that many different numbers will satisfy (not "solve") most inequalities. Cuddlyable3 (talk) 15:08, 15 June 2008 (UTC)
- See my comment above. -- Meni Rosenfeld (talk) 14:19, 15 June 2008 (UTC)
THIS WAS HOMEWORK.......I HAVE THE SAME CLASS for AXIA COLLEGE!!!!
Euler-Lagrange equations - The inverse problem
Is there a way to numerically compute the Lagrangian of a system, given a path that the system followed? 212.143.139.133 (talk) 11:08, 15 June 2008 (UTC)
- What a good question! Historically, the path of planet Mars was observed and recorded numerically by Tycho Brahe. Then the data were reduced into physical laws by Johannes Kepler. Further reductions by Isaac Newton and Joseph-Louis Lagrange lead to the Lagrangian. So yes, there is a way! Usually the induction of a physical law from experimental observations is more tricky than the deduction of an experimental result from the physical laws. Bo Jacoby (talk) 10:25, 16 June 2008 (UTC).
- Does a numerical algorithm for solving this kind of problems exist? I am particularly interested in a one dimensional system. Will I be needing more than one path in order to solve the problem? 212.143.139.133 (talk) 11:18, 16 June 2008 (UTC)
- If the motion is periodic, then the energy is conserved. If the kinetic energy as a function of velocity is (1/2)mv^2, then you can numerically compute kinetic energy as a function of position, and from that a table of potential energy as a function of position. Then you need to compute an interpolating function of the table. As several interpolating functions are possible, your solution is not unique. Several paths might improve certainty. Bo Jacoby (talk) 12:20, 16 June 2008 (UTC).
- Unfortunately, the motion is not periodic, it is very general. Furthermore, the potential itself changes all the time and I am not even sure that L=T-U. I guess it is quite a problem!
I am looking for a numerical algorithm which will help me approximate a family of Lagrangians based on paths of the one-dimensional system. 212.143.139.133 (talk) 07:41, 17 June 2008 (UTC)
- Unfortunately, the motion is not periodic, it is very general. Furthermore, the potential itself changes all the time and I am not even sure that L=T-U. I guess it is quite a problem!
Will they ever give up on this pi thing?
I mean, what the heck are the practical implications of finding the last number (if there is one)? Billions of places? Why?--Sam Science (talk) 13:28, 15 June 2008 (UTC)
- There is no last digit, and it has no practical implications (except possibly the testing of new computers). I doubt everyone's going to give up on it any time soon, though: many people seem to enjoy it. Me, I prefer e. Algebraist 13:35, 15 June 2008 (UTC)
- I guess it could help a little in answering the question of whether or not pi is normal. Obviously, an actual proof is needed to answer the question completely, but calculating enough digits could provide strong evidence against normality (I don't think it can really provide much evidence in favour of it). At least then, people would know what to try and prove. --Tango (talk) 14:53, 15 June 2008 (UTC)
And when they've finished with that, they should have one of thier interns take atom inventory.Sam Science (talk) 14:25, 15 June 2008 (UTC)
Question: I see from the article that e has been calculated up to 100 billion decimal places. Has it been done with only one algorithm or piece of software? If so, how do we know it's correct? Zain Ebrahim (talk) 14:35, 15 June 2008 (UTC)
- I don't know about e, but when people calculate digits of pi, they will use two algorithms and compare the answers. See here for one of the most recent announcements, explaining the process. I expect the same applies to e. --Tango (talk) 14:53, 15 June 2008 (UTC)
If you had an idea for an algorithm that could compute the digits of pi that ran fast enough to find more digits than anyone has ever found before, how could you resist the urge the write and run it? GromXXVII (talk) 17:37, 15 June 2008 (UTC)
- <joke> calculating enough digits of pi might also uncover secret messages. </joke> Oliphaunt (talk) 21:24, 15 June 2008 (UTC)
- If pi is normal, you will uncover all possible secret messages... eventually. JohnAspinall (talk) 20:53, 16 June 2008 (UTC)
June 16
trigonometry
How can we calculate sin 18 —Preceding unsigned comment added by Rohit max (talk • contribs) 05:36, 16 June 2008 (UTC)
- See Exact trigonometric constants#How can the trigonometric values for sine and cosine be calculated?. --Prestidigitator (talk) 07:47, 16 June 2008 (UTC)
Mensuration
How can we calculate the volume of prism? And of Pyramid? —Preceding unsigned comment added by Rohit max (talk • contribs) 05:45, 16 June 2008 (UTC)
- Try checking our articles on prisms and pyramids. Maelin (Talk | Contribs) 05:54, 16 June 2008 (UTC)
Image of a set
I feel myself very dumb, but... I have a R^2 set S whose image set Z in R^2 should be illustrated. The image set Z consists of vectors z1 and z2 that are represented by functions f1(x1,x2) and f2(x1,x2), respectively. I know how to illustrate S, but how to illustrate Z? How do I 'convert' the vectors in x1,x2 coordinates into vectors in z1,z2 coordinates? —Preceding unsigned comment added by 82.130.19.65 (talk) 09:26, 16 June 2008 (UTC)
- You have a mapping . To find the z-vectors, you just need to know the x-vectors and the functions f_1 and f_2. -mattbuck (Talk) 10:04, 16 June 2008 (UTC)
- Thanks mattbuck, that helps. But still, say I have a set S constrained by and , and the functions are determined by and , where the parameters can assume values from . I just don't "get" how to relate Z to S. 82.130.19.65 (talk) 06:09, 17 June 2008 (UTC)
antiderivative.. help!
Anyone feel like having a crack at:
ʃe/x dx
or more specifically the function I started out with ʃe(1-a/x) dx
(More specifically the integral between z and infinity where z is positive real, and z=a, k will be negative..).. Also the second (double) integral as well if you get the first..
Hints also appreciated. (87.102.86.73 (talk) 16:44, 16 June 2008 (UTC)
- Integration by parts will reduce it to the exponential integral. Oded (talk) 17:01, 16 June 2008 (UTC)
- is Exponential_integral#Convergent_series (these two covergent series) the best I can expect in terms of ease of calculation..? If so it looks like I would do 'just as well' as expressing the original function as a power series, integrating, and then evaluating (in terms of 'computer arithmetic time'). Thanks. Are there any other options?87.102.86.73 (talk) 18:58, 16 June 2008 (UTC)
- I have to admit I was hoping for a clever substitution I hadn't thought of that would reduce the integral to a sumless form.. such is optimism.87.102.86.73 (talk) 19:00, 16 June 2008 (UTC)
- The advantage in converting it to Ei is that Ei is probably better studied, in terms of its relationships to other functions. Perhaps there is also knowledge out there about efficient ways to calculate it and even ready-made routines. Oded (talk) 19:22, 16 June 2008 (UTC)
Percentages help
70% of my math mark is 68%. What if the other 30% (my final exam) is a big fat 0%? How would I put these together to find out my final mark?--Richard (Talk - Contribs) 22:46, 16 June 2008 (UTC)
- Well, I assume you mean that you have scored 68% average over the first 70% of the course, rather than having 68% from 70% possible so far. It's pretty simple, multiply 0.7 by 0.68 to get your current percentage mark, then add on 0.3 times your exam mark. -mattbuck (Talk) 23:20, 16 June 2008 (UTC)
- (ec) What you need to do is take a weighted average of the two scores, 68% and 0%, using respective weights of 70% and 30%. So you have 68%*70% + 0%*30% = 68% * 0.7 = 47.6%. Suppose the pass mark were 50%, then you could find out what you need to get in the final to pass - you need an extra 2.4%, and dividing that by 0.3 gives a total of 8 marks needed. (If you're interested, see what your maximum mark is, assuming you ace the final.) Confusing Manifestation(Say hi!) 23:22, 16 June 2008 (UTC)
That works, ConMan. Thanks. If I get a 0 on the exam, I'll have a 47.6%, though if I ace it, I'll get a 77.6%. Hopefully I'll get over 50 to pass... Thanks for your help guys.--Richard (Talk - Contribs) 00:21, 17 June 2008 (UTC)
June 17
Arithmetic
shanu 07:42, 17 June 2008 (UTC)Suppose than x,y,z are real numbers not equal to zero. a & b are two negative real nos. Is it always possible to find another real no. c such that x + y = z . For example consider 2 + 3 = 1.2 . I am thinking of this because fermat's last theorem doesen't allows it for natural nos. greater than 2.
- For any given x, y, a and b values the left side of your equation is some constant value: v = x + y. Then the equation v = z with given z has a solution defined by logarithm: c = logzv = log v / log z. --CiaPan (talk) 07:59, 17 June 2008 (UTC)
Cube Root
How can we find cube root of any no. ,like 2 without using calculator? —Preceding unsigned comment added by Rohit max (talk • contribs) 07:59, 17 June 2008 (UTC)
- We can use a paper and a pencil. Possibly Tables of logarithms, too... --CiaPan (talk) 08:02, 17 June 2008 (UTC)
- Without a log table it's a little harder. A good way to do it would be to start at some estimate and repeatedly iterate . -- Meni Rosenfeld (talk) 08:54, 17 June 2008 (UTC)
- Perhaps this will also be interesting. Not very effective for pen and paper, though. -- Meni Rosenfeld (talk) 09:10, 17 June 2008 (UTC)
- Apparently, there are a couple of "paper and pencil" algorithms for finding cube roots. This is one example (haven't checked it out, to be honest). Pallida Mors 01:41, 18 June 2008 (UTC)
- The simplest way is by the bisection method. Of course, if you actually mean *any* number, you'd have to consider calculating sines and cosines as well...--Fangz (talk) 01:55, 18 June 2008 (UTC)
-3^2 = ?
I brain farted with the initial question, asking 9^9. This is why Meni answered 'wrongly' - it's my fault -- 88.217.28.51 (talk) 08:54, 17 June 2008 (UTC)
Hi all,
-3^2 = 9
vs
-3^2 = -9
Which is correct? We can't agree, so I am asking here.. -- 88.217.28.51 (talk) 08:43, 17 June 2008 (UTC)
- See Order of operations. Exponentiation takes precedence over negation. Thus to evaluate -9^2, we first replace 9^2 with 81, giving -81. Thus -9^2 = -81. If we wanted to do the negation first, we would use parentheses: (-9)^2 = (-9)*(-9) = 81. -- Meni Rosenfeld (talk) 08:49, 17 June 2008 (UTC)
^ vs **
Now, they claim that ^ (not the XOR kind) and ** are different operators. Opinions on that one? -- 88.217.28.51 (talk) 10:38, 17 June 2008 (UTC)
- What is the context? In what way do "they" claim the operators are different? ** is not used in mathematical writing, only in some programming languages. Some languages use ^ to mean exponentiation, and some use **. I do not know of any other difference. -- Meni Rosenfeld (talk) 10:47, 17 June 2008 (UTC)
- My thoughts exactly. Thanks -- 88.217.28.51 (talk) 10:52, 17 June 2008 (UTC)
- The only language I know of that distinguishes between them is Haskell. ^ raises any number to an non-negative integer power (thus the result can have the same type as the base even in the case of integers, and it can be computed by repeated multiplication). ** raises numbers to floating-point powers and gives a floating-point result (in this case we can make no guarantee about whether the result is an integer or even rational, and we have to use a different algorithm to calculate the value). --Taejo|대조 11:51, 17 June 2008 (UTC)
- Python is another example. ** is exponentiation and ^ is XOR. Dragons flight (talk) 16:04, 18 June 2008 (UTC)
June 18
Constant rule of differentiation
Constant rule states that derivative of any constant is zero:
let y=c.
Why should 0/0 be 0 rather than undefined?--218.102.124.108 (talk) 05:24, 18 June 2008 (UTC)
- Because limit of the ratio of two functions is not necessarily equal the ratio of limits of those functions. Anyway check the limit's definition, and see that values of 0/Δx are arbitrarily close to zero when Δx approaches zero (in fact they are all equal zero), so they satisfy conditions in the limit definition. --CiaPan (talk) 05:47, 18 June 2008 (UTC)
- Your mistake is in the step . Taking a limit is not the same as plugging in a value for the function; that is, is not necessarily (if it was, we wouldn't invent limits in the first place). The correct steps are . If you make this mistake it will happen when you calculate any derivative, not just for a constant. Do read up on the definition of limits. -- Meni Rosenfeld (talk) 08:28, 18 June 2008 (UTC)
- More specifically, you can 'plug in' limits like that, provided the denominator does not equal zero, as it does in your case.--Fangz (talk) 11:51, 18 June 2008 (UTC)
- You can plug in values if the function is continuous at the point. It is true that for rational functions, this happens exactly when the denominator is not zero at the point. Not all functions are rational, though. -- Meni Rosenfeld (talk) 12:54, 18 June 2008 (UTC)
- Thanks everyone. I think I've known what's wrong with me. But what I intended to solve is 0/0:
- So what is the result of 0/0?--218.102.124.108 (talk) 15:34, 18 June 2008 (UTC)
- 0/0 is undefined in all common structures. See division by zero. -- Meni Rosenfeld (talk) 15:38, 18 June 2008 (UTC)
- , and that's true for any number x (it can also be true for infinity in some circumstances), so basically 0/0 can equal anything. If you end up with a 0/0 somewhere, you have to go back a step and work it out a different way, because it could come out to be absolutely anything. For example, if f(x)=0/x, then, if you want f to be continuous, you have to set f(0)=0, but if f(x)=x/x then f(0)=1, or if f(x)=2x/x, then f(0)=2. (Those are pretty trivial examples, but they should give you an idea of what can happen.) --Tango (talk) 15:52, 18 June 2008 (UTC)
- The string of characters "0/0" can mean two different things. It can mean an attempt to divide 0 by 0, in which case it can't equal anything as it is undefined. It can also mean a certain Indeterminate form, in which case it could indeed evaluate to anything, but is only a mnemonic, not an actual mathematical entity. -- Meni Rosenfeld (talk) 16:05, 18 June 2008 (UTC)
- Yes, I should have been clear I was speaking very informally, just to give an idea of why it is undefined. --Tango (talk) 16:18, 18 June 2008 (UTC)
- The string of characters "0/0" can mean two different things. It can mean an attempt to divide 0 by 0, in which case it can't equal anything as it is undefined. It can also mean a certain Indeterminate form, in which case it could indeed evaluate to anything, but is only a mnemonic, not an actual mathematical entity. -- Meni Rosenfeld (talk) 16:05, 18 June 2008 (UTC)
- You can plug in values if the function is continuous at the point. It is true that for rational functions, this happens exactly when the denominator is not zero at the point. Not all functions are rational, though. -- Meni Rosenfeld (talk) 12:54, 18 June 2008 (UTC)
- More specifically, you can 'plug in' limits like that, provided the denominator does not equal zero, as it does in your case.--Fangz (talk) 11:51, 18 June 2008 (UTC)
cubic metres, cubic kilometers
A recent article about the Niger Delta talked about "10 trillion cubic meters of natural gas reserves" in one region there, and "28,800 cubic km" (kilometres, we assume) of natural gas reserves is Russia. Too many zeroes...will 1000 cubic meters be 1 cubic kilometre, and therefore 28,800 cubic km, will be 28,800,000 cubic meters...which is only 28.8 million cubic meters...which must be way less than 10 trillion (10,000,000,000,000 (is a trillion a thousand billion?)...So the Niger Delta reserves in this one region are millions of times more than the reserves in Russia? Surely we are confused over the math, but maybe the press was wrong. Can anyone confirm or correct our understanding? Thanks if you can help. —Preceding unsigned comment added by 213.84.41.211 (talk) 14:20, 18 June 2008 (UTC)
- There are 1000 meters in a kilometer, but 1000^3 = 1,000,000,000 cubic meters in a cubic kilometer. Wikiant (talk) 14:27, 18 June 2008 (UTC)
- So there are in fact 29 trillion cubic meters of gas in Russia. I think mass is a much more useful measure for the quantity of a gas then volume, though. -- Meni Rosenfeld (talk) 15:36, 18 June 2008 (UTC)
- Agreed. I don't think Nigeria is the same temperature as Russia. Algebraist 15:42, 18 June 2008 (UTC)
- It might be underground, though. At least, there is probably less of a difference. --Tango (talk) 15:48, 18 June 2008 (UTC)
- I think such measures are based on what the real volume would be under certain standardized conditions. See Natural gas#Energy content, statistics and pricing. PrimeHunter (talk) 00:04, 19 June 2008 (UTC)
- I figured as much, but I still find it unnecessarily confusing. -- Meni Rosenfeld (talk) 11:49, 19 June 2008 (UTC)
- I think such measures are based on what the real volume would be under certain standardized conditions. See Natural gas#Energy content, statistics and pricing. PrimeHunter (talk) 00:04, 19 June 2008 (UTC)
- It might be underground, though. At least, there is probably less of a difference. --Tango (talk) 15:48, 18 June 2008 (UTC)
- Agreed. I don't think Nigeria is the same temperature as Russia. Algebraist 15:42, 18 June 2008 (UTC)
- So there are in fact 29 trillion cubic meters of gas in Russia. I think mass is a much more useful measure for the quantity of a gas then volume, though. -- Meni Rosenfeld (talk) 15:36, 18 June 2008 (UTC)
In answer to the side question, most people writing about numbers that big in English use a billion to mean 1,000,000,000 (10) and a trillion to mean 1,000,000,000,000 (10). But until recent decades, it was usual in English outside of North America for a billion to mean 1,000,000,000,000 (10) and a trillion 1,000,000,000,000,000,000 (10). The cognate words in most other languages have the larger meanings, and some people still prefer them for use in English. See long and short scales (and please do not debate them here). --Anonymous, 02:27 UTC, June 19, 2008.
- A billion being a thousand million is pretty much universal these days. There's no need to worry about possible alternatives. --Tango (talk) 11:58, 19 June 2008 (UTC)
Random numbers
Random numbers may be generated on computers, graphing calculators, and even Excel spreadsheets. (Although these are technically referred to as "pseudo" random numbers, that distinction is irrelevant for purposes of this question.) The following scenario came to mind, from which this question arises. Let's say that a teacher asks his students, as a homework practice exercise, to generate 5 random numbers, with each random number ranging from 0 to 9 inclusively. So, for example, one student might generate 3, 7, 2, 1, 9. Another student might generate 5, 6, 3, 5, 2. And so forth. Now, say there is a lazy student who did not do the homework and, when asked, lies to the teacher and fabricates that he generated 7, 7, 7, 7, 7. (Also, indicating a none-too-bright student, as he could just as easily have lied with a less "suspicious" result of another fictitious string of numbers such as, say, 4, 1, 8, 3, 0 or so.) So, the teacher gets suspicious at the result of 7, 7, 7, 7, 7, and suspects that the student cheated and did not, in fact, actually do the homework assignment. So, here is my question. Should the teacher, in fact, get suspicious at such a result? Is a result such as 7, 7, 7, 7, 7 equally likely as a series of 5 different digits (say, 3, 8, 0, 2, 6) … or is such a result not as equally likely in the generating of random numbers? My understanding is that any (and all) of the 5 separate digits is randomly generated and, thus, a result such as 7, 7, 7, 7, 7 should not be a surprising result. But, my gut instinct also tells me that it is highly unlikely to generate a result such as 7, 7, 7, 7, 7 and that a mixture of different digits is much more likely / probable. What is the truth of the matter? If all 5 digits are randomly generated, why does a result like 7, 7, 7, 7, 7 seem so improbable? Any insights? Thanks. (Joseph A. Spadaro (talk) 23:23, 18 June 2008 (UTC))
- There are more than one way to answer this; I'll pick the one that seems most in line with your motivation. It all comes down to Bayes' law. Let A be the event "student cheated", B be "Student chose 38026", C be "student chose 77777". Assume P(A)=10% and that a cheating student can only come up with a constant sequence, thus P(C|A)=10%. Then , while . Of course you can replace the assumptions with whatever you find reasonable to get more realist estimates. -- Meni Rosenfeld (talk) 23:36, 18 June 2008 (UTC)
- Theoretically a computer can generate a random number, not just a pseudorandom number. Although in my opinion and ignorance of physics, I am under the belief that of what’s on the market, only the quantum random number generators can be truly random, and those will cost as much as the computer to run them.
- As for the actual question… I would try to find some way of measuring how random a number “looks”. Very subjective, but 2 4 9 5 2, 9 5 2 3 1, and 7 7 7 7 7 are all equally likely, but like most normal people my first reaction wouldn’t be to question the first two, but would be the third: because there are a lot of numbers that “look like” the first two, but only a few if any numbers that “look like” the third. GromXXVII (talk) 23:57, 18 June 2008 (UTC)
- (e/c)Random is as random does - but human brains are very good at spotting patterns, even when they're spurious. Write down what you think would be 50 perfectly random coin tosses, and you're not likely to write down any sequence with more than 3 or 4 heads in a row. And yet, you're actually quite likely to get a run of 5, which you will find if you actually do the coin tosses a few times. The run of 5 heads is a pattern, and since we don't expect to see patterns in "random" data, it throws us.
- That said, if you see something "odd", then you can perform a hypothesis test to see if it's statistically unlikely. First, you get an idea of what the results would look like if they were selected randomly - say, with each digit uniformly distributed between 0 and 9. Then you quantify just what is "odd" about Johnny's 7, 7, 7, 7, 7 (i.e. "it's the same digit 5 times). Finally, you calculate the probability that you would find a result equally as odd as or more odd than Johnny's, and from that probability determine whether it still seems unlikely (5% is a common cutoff, 1% if you're being more lenient). The probability of getting 5 digits the same is 1/1000, or 0.1%, so Johnny might be looking a little nervous right now.
- And for the silly answer, both students fail. The perfectly random selection would be 4, 4, 4, 4, 4. Confusing Manifestation(Say hi!) 00:06, 19 June 2008 (UTC)
- Some more thoughts:
- 77777 has a lower Kolmogorov complexity than 38026. This is why a cheater with no access to an adequate RNG is more likely to generate 77777 than 38026.
- While 77777 is as likely as 38026, there are simple associated variables that are not equilikely. For example, you can define a variable "how many different digits are in the sequence". This will be 5 with probability ≈30%, and 1 with probability 0.01%.
- Occam's razor says the simplest explanation to an observation tends to be the correct one. The sequence 38026 is not likely to occur, but if it does occur, the only explanation is that it happened randomly (again assuming that without a RNG it's difficult to come up with it). If, however, we are presented with 77777, the simplest explanation is that the student cheated.
- -- Meni Rosenfeld (talk) 00:14, 19 June 2008 (UTC)
- Some more thoughts:
- Here are some approximate odds (I didn't want to use a calculator to find the exact odds):
- Chances of a given student picking 7 7 7 7 7 exactly: 1 in 100,000.
- Chances of a given student picking any number 5 times in a row: 1 in 10,000.
- Chances of any student in a class of 25 picking any number 5 times in a row: 25 in 10,000 or 1 in 400.
- Chances of any student in a 8 classes of 25 each picking any number 5 times in a row: 200 in 10,000 or 1 in 50.
- Chances of any student in a 8 classes of 25 each picking any number 5 times in a row or any sequence of 5 numbers in a row (0-4, 1-5, 2-6, 3-7, 4-8, 5-9, 6-0, 7-1, 8-2, 9-3): 200 in 5,000 or 1 in 25.
- Add in reverse sequences like 9 8 7 6 5 and even sequences like 0 2 4 6 8 and odd sequences like 1 3 5 7 9 and now reverse those, too, and there's a good chance that one student would hit one of those. StuRat (talk) 00:17, 19 June 2008 (UTC)
- I don't think that's a good argument. There's a lot of reason to think that a student without a RNG can just make up a number like 38026, and it's arguable that a number like 77777 is unlikely to arise out of a student told to work out a random number generation and thus *more* likely to be random. (In fact, IIRC, there's good evidence that in human generated sequences, usually runs of numbers are *less* common than in actual random numbers, especially in the binary case.) Trying to find ways that 77777 is special is also very dangerous, since the arguments previously put forward are equally applicable to any finite sequence. Even something like Kolmogorov complexity isn't helpful, because you can easily define a post-facto language where 38026 is easy to generate while 77777 is not. (E.g. 38026 can be someone's birthday, while 77777 cannot)
- I think the probably best way to deal with the problem is a bayesian approach. You need to pre-specify an impression of what a human generated sequence is like, and what a good rng is like, and set some prior probabilities. Then just update your beliefs. Specifically, there isn't a good way to just say a probability - your view of whether the sequence is random or not can only be stated relative to a well (and in advance, especially not based on perceived specialness of the sequence) defined alternative hypothesis and/or a set of priors.--Fangz (talk) 00:48, 19 June 2008 (UTC)
- You have raised the psychological warfare issue - "the student knows I will suspect 77777, and thus will avoid it if he cheats". The problem with this is that it can always be taken one step further - "The student knows I know he knows, and thus will choose 77777 if he cheats in order to trick me". It's thus not very reliable reasoning.
- You say that trying to find projections from the space of sequences to a lower-dimensional space in which 77777 is projected to a salient outcome is dangerous. However, it is only dangerous if the projection is complicated and arbitrary. For example, we could define " is 0 if , otherwise ". Then will have a very low probability, so we will reject an answer of 38026. However, this projection is very arbitrary and silly. If we stick to something simple and natural, like " is the number of distinct digits in ", we should be good.
- In your Bayesian framework, you say we need "an impression of what a... sequence is like". But this can only be formalized in terms of some projection like above. The essence of your suggestion is that instead of arbitrarily choosing the probability of a student cheating and the distribution of given that he is, we should calculate them based on observations. However, such observations are hard to come by. Cheating students will generally not admit to doing so, and asking random students to invent their own sequences may not give you a lot of insight into the mind of the cheater.
- -- Meni Rosenfeld (talk) 11:45, 19 June 2008 (UTC)
- If you want to get psychological you also need to account for the fact that if a student genuinely gets 7,7,7,7,7 out of a RNG, they are likely to think something has gone wrong and do it again. --Tango (talk) 15:04, 19 June 2008 (UTC)
- I think the probably best way to deal with the problem is a bayesian approach. You need to pre-specify an impression of what a human generated sequence is like, and what a good rng is like, and set some prior probabilities. Then just update your beliefs. Specifically, there isn't a good way to just say a probability - your view of whether the sequence is random or not can only be stated relative to a well (and in advance, especially not based on perceived specialness of the sequence) defined alternative hypothesis and/or a set of priors.--Fangz (talk) 00:48, 19 June 2008 (UTC)
Basically, to give a sensible assignment like that, you should ask for enough numbers that a sensible randomness test will give a clear answer. Say you ask for 200 numbers and you get the following output from a student:
- 1549248135779511892489513549165798
- 7691249876216984798416498765194327
- 9165498732498490987951979164984691
- 9498496519496195498795195746249832
- 4981951976249519762495462498746579
- 5162195762169795194957264916
Did he do this by tapping on a keyboard or by using a RNG? (Hint - I am lazy!) So maybe you can do the chi-square test and the runs test and get a pretty good answer. --Slashme (talk) 13:52, 19 June 2008 (UTC)
Maybe the runs test isn't very sensitive! For example, for the numbers I gave (monkey style), I got a runs test value of -1.2535104, giving a P-value of 0.10601 and for 200 random numbers from Excel, I got a runs test result of -1.5420651, giving a P-value of 0.06258. (done using a javascript applet found on the web, so maybe there's a bug? I'm too lazy to check the code for correctness) --Slashme (talk) 14:40, 19 June 2008 (UTC)
June 19
Infinite Series Involving Prime Numbers
I came across the following series while studying some Fourier Analysis. Given the infinite series
After writing it in the following closed form
where returns the n-th prime number. Now this series seems to be converging and in fact it seems to be converging to a numerical value of . My question is, how can we tell for sure if this series is converging or not and if it is converging, what is it converging to? Is there anyway to find out what the exact value is? Is this a well-known fact, a well-known constant?A Real Kaiser (talk) 01:49, 19 June 2008 (UTC)
- The series certainly converges, by the alternating series test. Have you tried Plouffe's inverter for the limit (I don't have a precise enough estimate)? Algebraist 01:13, 19 June 2008 (UTC)
Actually no, I had not tried looking up in the inverter. I want to but the problem is that this series converges so slowly, after adding up the first 100,000 terms, I still only had 1.04693... and I am not even sure about the last digit 2 yet. So, first I have to write up a more efficient program to calculate more digits (faster) so that I can obtain more decimal places. Meanwhile, does anyone have any idea what this number is?A Real Kaiser (talk) 01:49, 19 June 2008 (UTC)
- I'm fairly certain it starts 1.046932971... (with the last 1 possibly a 0). Plouffe's returns no hits. -- Meni Rosenfeld (talk) 09:56, 19 June 2008 (UTC)
- See Proof that the sum of the reciprocals of the primes diverges -- Q Chris (talk) 10:32, 19 June 2008 (UTC)
- How is this relevant? -- Meni Rosenfeld (talk) 10:47, 19 June 2008 (UTC)
I think I've found it on OEIS: - note that their formulation differs from yours, because you've omitted 2 and 3, and included 1.Oops, didn't notice the oddity in your thing. It isn't the same after all. Well, maybe that's a start, at least.--Fangz (talk) 11:35, 19 June 2008 (UTC)
Maths (Indian mathematicians)
How do I get the clips of Sridhara on wikipedia?Minintelligent (talk) 10:52, 19 June 2008 (UTC)
- What do you mean by "clips"? You can add pieces of information to the Sridhara article if you have anything suitable. If you are having trouble with editing then you should try reading Misplaced Pages:How to edit a page, which gives lots of assistance. --tiny plastic Grey Knight ⊖ 11:55, 19 June 2008 (UTC)
Meaning of Exponent In Trigonometric Expressions?
What does mean?
And
And ?
Etc.
The Piano Man (talk) 14:14, 19 June 2008 (UTC)
- means or equivently . It is used to distinguish easily from . Similarly the same rule applies for the other trig functions. Rambo's Revenge (talk) 14:32, 19 June 2008 (UTC)
- It's important to note that for most other functions, the same notation means to apply the function twice, . The way it's used for trig function is an abuse of notation, but it's a very convenient one. --Tango (talk) 14:39, 19 June 2008 (UTC)
- Be careful though, as , but is instead equal to . -mattbuck (Talk) 15:20, 19 June 2008 (UTC)
- And if you see , it's best just to run away and hide! --Tango (talk) 15:27, 19 June 2008 (UTC)
- Be careful though, as , but is instead equal to . -mattbuck (Talk) 15:20, 19 June 2008 (UTC)
savant mathématicien
Bonjour, Pourquoi M.Jan MIKUSINSKI né le 3 avril 1913 à Stanislawow et décédé le 27 juillet 1987 à KATOWICE ne figure pas dans la liste des grands mathématiciens connu pour son travail de pionnier dans l'analyse mathématique.M.Mikusinski a développé un calcul opérationnel 44a40 calculus of Mikusinski,qui sont pertinentes pour résoudre les équations différentielles.Son calcul opérationnel est basé sur un calcul de la convolution des fonctions à l'égard de la transformés de Fourier.De la convolution produit qu'il va à définir ce que dans d'autres contextes est appelé le domaine de fractions ou un quotient domaine.Ces couples de fonctions M.Mikusinski appels opérateurs-Mikusinski opérateur,44a40 il est également bien connu pour Cube et Antosik-Mikusinski Théorem,Mikusinski convolution algèbre etc. Récupéré "de http://en.wikipedia.org/Jan_Mikusinski" Plusieurs grands savants polonais figurent aux États-Unis en Suède et font des conférences partout dans le monde. La Pologne peut être très fière d'avoir des savant d'une telle renommée dans le monde entier. —Preceding unsigned comment added by 90.54.102.79 (talk) 14:41, 19 June 2008 (UTC)
 then
then  so you could think of starting from
so you could think of starting from  (as long as you do it consistently). –
(as long as you do it consistently). – 
![{\displaystyle x=C-{\sqrt {\frac {2}{-1+C}}}\left((-1+C){\text{EllipticE}}\left}}}\right],{\frac {1+C}{-1+C}}\right]+{\text{EllipticF}}\left}}}\right],{\frac {1+C}{-1+C}}\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba12e0c63f3ea19f7c10c8b06826b87b398b4407)
 . You get a separable equation:
. You get a separable equation:
 —
—  trick standard?
trick standard?  .
.  . You see that multiplying both sides by minus 2 gives
. You see that multiplying both sides by minus 2 gives  . That demonstrates the inequality sign turning around. Equations don't contain inequality signs, instead they have an equals sign that doesn't change, as long as you multiply or divide both sides by the same (any) number.
. That demonstrates the inequality sign turning around. Equations don't contain inequality signs, instead they have an equals sign that doesn't change, as long as you multiply or divide both sides by the same (any) number. is an equation and its solution is
is an equation and its solution is  . You know this solution is right because
. You know this solution is right because  times
times  indeed equals 12. Note that many different numbers will satisfy (not "solve") most inequalities.
indeed equals 12. Note that many different numbers will satisfy (not "solve") most inequalities.  . To find the z-vectors, you just need to know the x-vectors and the functions f_1 and f_2. -
. To find the z-vectors, you just need to know the x-vectors and the functions f_1 and f_2. - and
and  , and the functions are determined by
, and the functions are determined by  and
and  , where the parameters can assume values from
, where the parameters can assume values from  . I just don't "get" how to relate Z to S.
. I just don't "get" how to relate Z to S.  and repeatedly iterate
and repeatedly iterate  . --
. -- 
 . Taking a limit is not the same as plugging in a value for the function; that is,
. Taking a limit is not the same as plugging in a value for the function; that is,  is not necessarily
is not necessarily  (if it was, we wouldn't invent limits in the first place). The correct steps are
(if it was, we wouldn't invent limits in the first place). The correct steps are  . If you make this mistake it will happen when you calculate any derivative, not just for a constant. Do read up on the definition of limits. --
. If you make this mistake it will happen when you calculate any derivative, not just for a constant. Do read up on the definition of limits. -- 
 , and that's true for any number x (it can also be true for infinity in some circumstances), so basically 0/0 can equal anything. If you end up with a 0/0 somewhere, you have to go back a step and work it out a different way, because it could come out to be absolutely anything. For example, if f(x)=0/x, then, if you want f to be continuous, you have to set f(0)=0, but if f(x)=x/x then f(0)=1, or if f(x)=2x/x, then f(0)=2. (Those are pretty trivial examples, but they should give you an idea of what can happen.) --
, and that's true for any number x (it can also be true for infinity in some circumstances), so basically 0/0 can equal anything. If you end up with a 0/0 somewhere, you have to go back a step and work it out a different way, because it could come out to be absolutely anything. For example, if f(x)=0/x, then, if you want f to be continuous, you have to set f(0)=0, but if f(x)=x/x then f(0)=1, or if f(x)=2x/x, then f(0)=2. (Those are pretty trivial examples, but they should give you an idea of what can happen.) -- , while
, while  . Of course you can replace the assumptions with whatever you find reasonable to get more realist estimates. --
. Of course you can replace the assumptions with whatever you find reasonable to get more realist estimates. --  is 0 if
is 0 if  , otherwise
, otherwise  ". Then
". Then  will have a very low probability, so we will reject an answer of 38026. However, this projection is very arbitrary and silly. If we stick to something simple and natural, like "
will have a very low probability, so we will reject an answer of 38026. However, this projection is very arbitrary and silly. If we stick to something simple and natural, like " ", we should be good.
", we should be good.

 returns the n-th prime number. Now this series seems to be converging and in fact it seems to be converging to a numerical value of
returns the n-th prime number. Now this series seems to be converging and in fact it seems to be converging to a numerical value of  . My question is, how can we tell for sure if this series is converging or not and if it is converging, what is it converging to? Is there anyway to find out what the exact value is? Is this a well-known fact, a well-known constant?
. My question is, how can we tell for sure if this series is converging or not and if it is converging, what is it converging to? Is there anyway to find out what the exact value is? Is this a well-known fact, a well-known constant? mean?
And
mean?
And  And
And  ?
Etc.
?
Etc.
 means
means  or equivently
or equivently  . It is used to distinguish easily from
. It is used to distinguish easily from  . Similarly the same rule applies for the other trig functions.
. Similarly the same rule applies for the other trig functions.  . The way it's used for trig function is an
. The way it's used for trig function is an  , but is instead equal to
, but is instead equal to  . -
. - , it's best just to run away and hide! --
, it's best just to run away and hide! --