| Revision as of 12:32, 1 March 2011 editBongomatic (talk | contribs)Autopatrolled, Extended confirmed users, Pending changes reviewers, Rollbackers15,898 editsm Reverted edits by Myles325a (talk) to last version by DreamGuy← Previous edit | Revision as of 01:37, 3 March 2011 edit undoMyles325a (talk | contribs)Extended confirmed users1,553 edits Undid revision 416547670 by Bongomatic (talk)Next edit → | ||
| Line 38: | Line 38: | ||
| ==External links== | ==External links== | ||
| * | * | ||
| *http://find-kenken-and-minuplu-puzzles.com/ (lists sites for kenken and its close variants) | |||
| *, ], March 2, 2009 | *, ], March 2, 2009 | ||
| {{DEFAULTSORT:Kenken}} | {{DEFAULTSORT:Kenken}} | ||
| ] | ] | ||
Revision as of 01:37, 3 March 2011
KenKen or KenDoku is a style of arithmetic and logic puzzle invented in 2004 by the Japanese math teacher Tetsuya Miyamoto, an innovator who says he practices "the art of teaching without teaching". He intends the puzzles as an instruction-free method of training the brain. The names Calcudoku and Mathdoku are sometimes used by those who don't have the rights to use the KenKen or KenDoku trademarks.
The name derives from the Japanese for cleverness (賢, ken, kashiko(i)).
As in sudoku, the goal of each puzzle is to fill a grid with digits –– 1 through 4 for a 4×4 grid, 1 through 5 for a 5×5, etc. –– so that no digit appears more than once in any row or column. Grids range in size from 3×3 to 9×9. Additionally, KenKen grids are divided into heavily outlined groups of cells –– often called “cages” –– and the numbers in the cells of each cage must produce a certain “target” number when combined using a specified mathematical operation (either addition, subtraction, multiplication or division). For example, a three-cell cage specifying addition and a target number of 6 in a 4×4 puzzle might be satisfied with the digits 1, 2, and 3. Digits may be repeated within a cage, as long as they are not in the same row or column. No operation is relevant for a single-cell cage: placing the "target" in the cell is the only possibility. The target number and operation appear in the upper left-hand corner of the cage.
In the English-language KenKen books of Will Shortz, the issue of the non-associativity of division and subtraction is addressed by restricting clues based on either of those operations to cages of only two cells. Some puzzle authors have not done this and have published puzzles that use more than two cells for these operations.
History
In 2005, toy inventor Robert Fuhrer encountered KenKen books published in Japan by the educational publisher Gakken Co., Ltd. and titled "Kashikoku naru Puzzle" (賢くなるパズル, kashikoku naru pazuru, lit. "smartness puzzle"). Fuhrer's company Nextoy, LLC (now holder of a trademark on "KenKen" and "KenDoku" as a name for brain-training puzzles) and chess International Master Dr. David Levy helped bring the puzzles to the attention of Michael Harvey, features editor of The Times (London). Harvey, impressed with what he calls its "depth and magnitude", arranged for publication of such puzzles, starting in March 2008, in The Times. Other papers, including the New York Times, followed suit. KenKen now appears in more than 40 newspapers in the United States, as well as numerous international publications.
Example
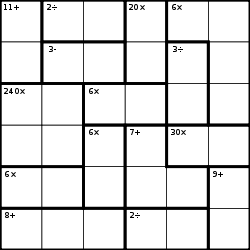

The objective is to fill the grid in with the digits 1 through 6 such that:
- Each row contains exactly one of each digit
- Each column contains exactly one of each digit
- Each bold-outlined group of cells is a cage containing digits which achieve the specified result using the specified mathematical operation: addition (+), subtraction (−), multiplication (×), and division (÷). (Unlike Killer Sudoku, digits may repeat within a group.)
Some of the techniques from Sudoku and Killer Sudoku can be used here, but much of the process involves the listing of all the possible options and eliminating the options one by one as other information requires.
In the example here:
- "11+" in the leftmost column can only be "5,6"
- "2÷" in the top row must be one of "1,2", "2,4" or "3,6"
- "20×" in the top row must be "4,5".
- "6×" in the top right must be "1,1,2,3". Therefore the two "1"s must be in separate columns, thus row 1 column 5 is a "1".
- "240×" on the left side is one of "6,5,4,2" or "3,5,4,4". Either way there is a five and it must be in the right pair of cells since we have "5,6" already in column 1.
- etc.
Extensions
More complex KenKen problems are formed using the principles described above but omitting the symbols +, −, × and ÷, thus leaving them as yet another unknown to be determined.
The restriction of puzzle size to the range two through nine is not absolute. A KenKen of size two is of little value even as an example, as it can immediately be solved by trying the two possibilities — ones on the "rising" diagonal and twos on the "falling" one, or vice versa. But extension beyond nine presents only difficulties of calculation with larger numbers, and the need, in recording possible values, to avoid confusing multi-digit numbers with items in a list of single digit ones.
References
- ^ A New Puzzle Challenges Math Skills, New York Times, February 8, 2009
- ^ Tetsuya Miyamoto creates KenKen. Train your brain, The Times, 21 March 2008
- KenDoku renamed to CalcuDoku
- Stephey, M. J. "The Next Sudoku?" Time Magazine 23 Mar. 2009: 72.
External links
- kenken.com (official site)
- http://find-kenken-and-minuplu-puzzles.com/ (lists sites for kenken and its close variants)
- Puzzle Guru Will Shortz, Time Magazine, March 2, 2009