| Revision as of 23:27, 23 December 2011 editSpinningspark (talk | contribs)89,216 edits →Ohm's law: Remove misleading statement← Previous edit | Revision as of 23:46, 23 December 2011 edit undoSpinningspark (talk | contribs)89,216 edits →Impedance and admittance: Remove misleading statements. R=1/G always for a given element in a circuit, but these two equations (impedance and admittance) imply different equivalent circuit representationsNext edit → | ||
| Line 136: | Line 136: | ||
| *<math>\omega</math> is the ] of the AC current, | *<math>\omega</math> is the ] of the AC current, | ||
| *<math>j=\sqrt{-1}</math> is the ]. | *<math>j=\sqrt{-1}</math> is the ]. | ||
| The impedance and admittance |
The impedance and admittance may be expressed as complex numbers which can be broken into real and imaginary parts: | ||
| :<math>Z=R+jX, \quad Y=G+jB</math> | :<math>Z=R+jX, \quad Y=G+jB</math> | ||
| where ''R'' and ''G'' are resistance and conductance respectively, ''X'' is ], and ''B'' is ]. For ideal resistors, |
where ''R'' and ''G'' are resistance and conductance respectively, ''X'' is ], and ''B'' is ]. For ideal resistors, ''Z'' and ''Y'' reduce to ''R'' and ''G'' respectively, but for AC networks containing ]s and ]s, ''X'' and ''B'' are nonzero. | ||
| <math>Z=1/Y</math> for AC circuits, just as <math>R=1/G</math> for DC circuits. | |||
| :<math>G=R/(R^2+X^2)</math> | |||
| On the other hand, <math>Z=1/Y</math> is always true in AC circuits. | |||
| ===Frequency dependence of resistance=== | ===Frequency dependence of resistance=== | ||
Revision as of 23:46, 23 December 2011
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical notion of friction. The SI unit of electrical resistance is the ohm (Ω), while electrical conductance is measured in siemens (S).
An object of uniform cross section has a resistance proportional to its resistivity and length and inversely proportional to its cross-sectional area. All materials show some resistance, except for superconductors, which have a resistance of zero.
The resistance of an object is defined as the ratio of voltage across it to current through it, while the conductance is the inverse:
For a wide variety of materials and conditions, V and I are directly proportional to each other, and therefore R and G are constant (although they can depend on other factors like temperature or strain). This proportionality is called Ohm's law, and materials that satisfy it are called "Ohmic" materials.
In other cases, such as a diode or battery, V and I are not directly proportional, or in other words the I–V curve is not a straight line through the origin, and Ohm's law does not hold. In this case, resistance and conductance are less useful concepts, and more difficult to define. The ratio V/I is sometimes still useful, and is referred to as a "chordal resistance" or "static resistance",, as it corresponds to the inverse slope of a chord between the origin and an I–V curve. In other situations, the derivative dV/dI may be most useful; this is called the "differential resistance".
The above discussion was for DC circuits. In the AC case, the resistance and conductance in ohm's law are generalized to impedance and admittance respectively in ohm's law, and the equation is not necessarily true, as discussed below.
Introduction

In the hydraulic analogy, current flowing through a wire (or resistor) is like water flowing through a pipe, and the voltage drop across the wire is like the pressure drop which pushes water through the pipe. Conductance is proportional to how much flow occurs for a given pressure, and resistance is proportional to how much pressure is required to achieve a given flow. (Conductance and resistance are reciprocals.)
The voltage drop (i.e., difference in voltage between one side and the other), not the voltage itself, is the driving force pushing current through a resistor. In hydraulics, it is similar: The pressure difference between two sides of a pipe, not the pressure itself, determines the flow through it. For example, there may be a large water pressure above the pipe, which tries to push water down through the pipe. But there may be an equally large water pressure below the pipe, which tries to push water back up through the pipe. If these pressures are equal, no water will flow. (In the image at right, the water pressure below the pipe is zero.)
The resistance and conductance of a wire, resistor, or other element is generally determined by two factors: Geometry (shape) and materials.
Geometry is important because it is more difficult to push water through a long, narrow pipe than a wide, short pipe. In the same way, a long, thin copper wire has higher resistance (lower conductance) than a short, thick copper wire.
Materials are important as well. A pipe filled with hair restricts the flow of water more than a clean pipe of the same shape and size. In a similar way, electrons can flow freely and easily through a copper wire, but cannot as easily flow through a steel wire of the same shape and size, and they essentially cannot flow at all through an insulator like rubber, regardless of its shape. The difference between, copper, steel, and rubber is related to their microscopic structure and electron configuration, and is quantified by a property called resistivity.
Conductors and resistors

Objects such as wires that are designed to have low resistance so that they transfer current with the least loss of electrical energy are called conductors. Objects that are designed to have a specific resistance so that they can dissipate electrical energy or otherwise modify how a circuit behaves are called resistors. Conductors are made of high-conductivity materials such as metals, in particular copper and aluminium. Resistors, on the other hand, are made of a wide variety of materials depending on factors such as the desired resistance, amount of energy that it needs to dissipate, precision, and cost.
Ohm's law

Ohm's law is an empirical law relating the voltage V across an element to the current I through it:
(V is directly proportional to I). This law is not always true: For example, it is false for diodes, batteries, etc. However, it is true to a very good approximation for wires and resistors (assuming that other conditions, including temperature, are held fixed). Materials or objects where Ohm's law is true are called "ohmic".
For ohmic materials, the resistance R and conductance G are defined by:
Therefore, resistance and conductance are inverses:
Relation to resistivity and conductivity
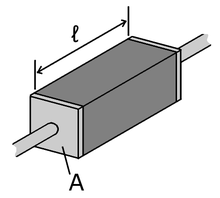
The resistance of a given object depends primarily on two factors: What material it is made of, and its shape. For a given material, the cross-sectional area is inversely proportional to the resistance; for example, a thick copper wire has lower resistance than an otherwise-identical thin copper wire. Also, for a given material, the resistance is proportional to the length; for example, a long copper wire has higher resistance than an otherwise-identical short copper wire. The resistance R and conductance G of a conductor of uniform cross section, therefore, can be computed as
where is the length of the conductor, measured in metres , A is the cross-section area of the conductor measured in square metres , σ (sigma) is the electrical conductivity measured in siemens per meter (S·m), and ρ (rho) is the electrical resistivity (also called specific electrical resistance) of the material, measured in ohm-metres (Ω·m). The resistivity and conductivity are proportionality constants, and therefore depend only on the material the wire is made of, not the geometry of the wire. Resistivity and conductivity are reciprocals: . Resistivity is a measure of the material's ability to oppose electric current.
This formula is not exact: It assumes the current density is totally uniform in the conductor, which is not always true in practical situations. However, this formula still provides a good approximation for long thin conductors such as wires.
Another situation for which this formula is not exact is with alternating current (AC), because the skin effect inhibits current flow near the center of the conductor. Then, the geometrical cross-section is different from the effective cross-section in which current is actually flowing, so the resistance is higher than expected. Similarly, if two conductors are near each other carrying AC current, their resistances will increase due to the proximity effect. At commercial power frequency, these effects are significant for large conductors carrying large currents, such as busbars in an electrical substation, or large power cables carrying more than a few hundred amperes.
What determines resistivity?
Main article: Electrical resistivity and conductivityThe resistivity of different materials varies by an enormous amount: For example, the conductivity of teflon is about 10 times lower than the conductivity of copper. Why is there such a difference? Loosely speaking, a metal has large numbers of "delocalized" electrons that are not stuck in any one place, but free to move across large distances, whereas in an insulator (like teflon), each electron is tightly bound to a single atom, and a great force is required to pull it away. Semiconductors lie between these two extremes. More details can be found in the article: Electrical resistivity and conductivity. For the case of electrolyte solutions, see the article: Conductivity (electrolytic).
Resistivity varies with temperature. In semiconductors, resistivity also changes when light is shining on it. These are discussed below.
Measuring resistance
Main article: ohmmeterAn instrument for measuring resistance is called an ohmmeter. Simple ohmmeters cannot measure low resistances accurately because the resistance of their measuring leads causes a voltage drop that interferes with the measurement, so more accurate devices use four-terminal sensing.
Typical resistances
See also: Electrical resistivities of the elements (data page) and Electrical resistivity and conductivity| Component | Resistance (Ω) |
| 1 meter of copper wire with 1mm diameter |
0.02 |
| 1km overhead power line (typical) |
0.03 |
| AA battery (typical internal resistance) |
0.1 |
| Incandescent light bulb filament (typical) |
200-1000 |
| Human body | 1000 to 100,000 |
Static and differential resistance
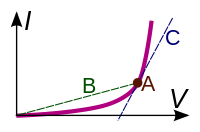 The IV curve of a non-ohmic device (purple). Point A represents the current and voltage values right now. The static resistance is the inverse slope of line B through the origin. The differential resistance is the inverse slope of tangent line C.
The IV curve of a non-ohmic device (purple). Point A represents the current and voltage values right now. The static resistance is the inverse slope of line B through the origin. The differential resistance is the inverse slope of tangent line C.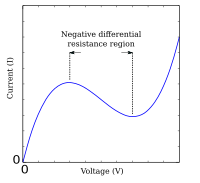 The IV curve of a component with negative differential resistance, an unusual phenomenon where the IV curve non-monotonic.
See also: Small-signal model
The IV curve of a component with negative differential resistance, an unusual phenomenon where the IV curve non-monotonic.
See also: Small-signal model
Many electrical elements, such as diodes and batteries do not satisfy Ohm's law. These are called non-ohmic, and are characterized by an I–V curve which is not a straight line through the origin.
Resistance and conductance can still be defined for non-ohmic elements. There are two common definitions:
where
- Rstatic is the static resistance, also called chordal resistance
- Rdifferential is the differential resistance, also called dynamic resistance, incremental resistance, or slope resistance. It is defined as the derivative of the IV relationship.
Both static and differential resistance depend on the operating point of the device; in other words, when the voltage across the element is changed, the resistance values change too.
The two definitions are useful in different circumstances. For example, when calculating the IR energy dissipated by an element (see below), the static resistance should be used. On the other hand, for small-signal modeling analysis of circuits, the differential resistance should be used.
If the V-I graph is not monotonic (i.e. it has a peak or a trough), the differential resistance will be negative for some values of voltage and current. This property is often known as negative differential resistance, sometimes (misleadingly) abbreviated as negative resistance. Examples of such elements include the tunnel diode and Gunn diode. Static resistance is negative only in devices that have an external source of power--for example, a battery or negative impedance converter.
AC circuits
Impedance and admittance
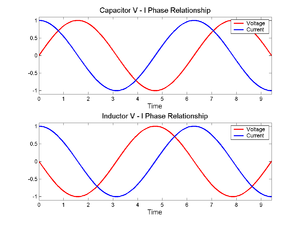
When an alternating current flows through a circuit, the relation between current and voltage across a circuit element is characterized not only by the ratio of their magnitudes, but also the difference in their phases. For example, in an ideal resistor, the moment when the voltage reaches its maximum, the current also reaches its maximum (current and voltage are oscillating in phase). But for a capacitor or inductor, the maximum current flow occurs as the voltage passes through zero and vice-versa (current and voltage are oscillating 90° out of phase, see image at right). Complex numbers are used to keep track of both the phase and magnitude of current and voltage:
where:
- t is time,
- V(t) and I(t) are, respectively, voltage and current as a function of time,
- V0, I0, Z, and Y are complex numbers,
- Z is called impedance,
- Y is called admittance,
- Re indicates real part,
- is the angular frequency of the AC current,
- is the imaginary unit.
The impedance and admittance may be expressed as complex numbers which can be broken into real and imaginary parts:
where R and G are resistance and conductance respectively, X is reactance, and B is susceptance. For ideal resistors, Z and Y reduce to R and G respectively, but for AC networks containing capacitors and inductors, X and B are nonzero.
for AC circuits, just as for DC circuits.
Frequency dependence of resistance
Another complication of AC circuits is that the resistance and conductance can be frequency-depedent. One reason, mentioned above is the skin effect (and the related proximity effect). Another reason is that the resistivity itself may depend on frequency (see Drude model, deep-level traps, resonant frequency, Kramers–Kronig relations, etc.)
Energy dissipation and Joule heating

Resistors (and other elements with resistance) oppose the flow of electric current; therefore, electrical energy is required to push current through the resistance. This electrical energy is dissipated, heating the resistor in the process. This is called Joule heating (after James Prescott Joule), also called ohmic heating or resistive heating.
The dissipation of electrical energy is often undesired, particularly in the case of transmission losses in power lines. High voltage transmission helps reduce the losses by reducing the current for a given power.
On the other hand, Joule heating is sometimes useful, for example in electric stoves and other electric heaters (also called resistive heaters). As another example, incandescent lamps rely on Joule heating: the filament is heated to such a high temperature that it glows "white hot" with thermal radiation (also called incandescence).
The formula for Joule heating is:
where P is the power (energy per unit time) converted from electrical energy to thermal energy, R is the resistance, and I is the current through the resistor.
Dependence of resistance on other conditions
Temperature dependence
Main article: Electrical resistivity and conductivity § Temperature dependenceNear room temperature, the resistivity of metals typically increases as temperatere is increased, while the resistivity of semiconductors typically decreases as temperature is increased. The resistivity of insulators and electrolytes may increase or decrease depending on the system. For the detailed behavior and explanation, see Electrical resistivity and conductivity.
As a consequence, the resistance of wires, resistors, and other components often change with temperature. This effect may be undesired, causing an electronic circuit to malfunction at extreme temperatures. In some cases, however, the effect is put to good use. When temperature-dependent resistance of a component is used purposefully, the component is called a resistance thermometer or thermistor. (A resistance thermometer is made of metal, usually platinum, while a thermistor is made of ceramic or polymer.)
Resistance thermometers and thermistors are generally used in two ways. First, they can be used as thermometers: By measuring the resistance, the temperature of the environment can be inferred. Second, they can be used in conjunction with Joule heating (also called self-heating): If a large current is running through the resistor, the resistor's temperature rises and therefore its resistance changes. Therefore, these components can be used in a circuit-protection role similar to fuses, or for feedback in circuits, or for many other purposes. In general, self-heating can turn a resistor into a nonlinear and hysteretic circuit element. For more details see Thermistor#Self-heating effects.
If the temperature T does not vary too much, a linear approximation is typically used:
where is called the temperature coefficient of resistance, is a fixed reference temperature (usually room temperature), and is the resistance at temperature . The parameter is an empirical parameter fitted from measurement data. Because the linear approximation is only an approximation, is different for different reference temperatures. For this reason it is usual to specify the temperature that was measured at with a suffix, such as , and the relationship only holds in a range of temperatures around the reference.
The temperature coefficient is typically +3×10 K to +6×10 K for metals near room temperature. It is usually negative for semiconductors and insulators, with highly variable magnitude.
Strain dependence
Main article: Strain gaugeJust as the resistance of a conductor depends upon temperature, the resistance of a conductor depends upon strain. By placing a conductor under tension (a form of stress that leads to strain in the form of stretching of the conductor), the length of the section of conductor under tension increases and its cross-sectional area decreases. Both these effects contribute to increasing the resistance of the strained section of conductor. Under compression (strain in the opposite direction), the resistance of the strained section of conductor decreases. See the discussion on strain gauges for details about devices constructed to take advantage of this effect.
Light illumination dependence
Main articles: Photoresistor and PhotoconductivitySome resistors, particularly those made from semiconductors, exhibit photoconductivity, meaning that their resistance changes when light is shining on them. Therefore they are called photoresistors (or light dependent resistors). These are a common type of light detector.
Superconductivity
Main article: SuperconductivitySuperconductors are materials that have exactly zero resistance and infinite conductance, because they can have V=0 and I≠0. This also means there is no joule heating, or in other words no dissipation of electrical energy. Therefore, if superconductive wire is made into a closed loop, current will keep flowing around the loop forever. Similarly, if a power line were made of a superconductor, there would be no transmission losses. Unfortunately, superconductors are almost never used for power lines, because they require liquid nitrogen cooling, and are expensive and delicate. They are, however, commonly used in NMR/MRI and a few other applications.
See also
- Electrical measurements
- Resistor
- Electrical conduction for more information about the physical mechanisms for conduction in materials.
- Voltage divider
- Voltage drop
- Thermal resistance
- Sheet resistance
- SI electromagnetism units
- Quantum Hall effect, a standard for high-accuracy resistance measurements.
- Series and parallel circuits
- Johnson–Nyquist noise
References
- ^ Forbes T. Brown (2006). Engineering System Dynamics. CRC Press. p. 43. ISBN 9780849396489.
- ^ Kenneth L. Kaiser (2004). Electromagnetic Compatibility Handbook. CRC Press. pp. 13–52. ISBN 9780849320873.
- Fink and Beaty, Standard Handbook for Electrical Engineers 11th Edition, page 17-19
- The resistivity of copper is about 1.7×10Ωm. See .
- Electric power substations engineering by John Douglas McDonald, p 18-37, google books link
- For a fresh Energizer E91 AA alkaline battery, the internal resistance varies from 0.9Ω at -40°C, to 0.1Ω at +40°C.
- A 60W light bulb in the USA (120V mains electricity) draws RMS current 60W/120V=500mA, so its resistance is 120V/500mA=240 ohms. The resistance of a 60W light bulb in Europe (230V mains) would be 900 ohms. The resistance of a filament is temperature-dependent; these values are for when the filament is already heated up and the light is already glowing.
- 100,000 ohms for dry skin contact, 1000 ohms for wet or broken skin contact. Other factors and conditions are relevant as well. See electric shock article for more details. Also see: "Publication No. 98-131: Worker Deaths by Electrocution". National Institute for Occupational Safety and Health. Retrieved 2008-08-16.
- Ward, MR, Electrical Engineering Science, pp36–40, McGraw-Hill, 1971.
- See Electrical resistivity and conductivity for a table. The temperature coefficient of resistivity is similar but not identical to the temperature coefficient of resistance. The small difference is due to thermal expansion changing the dimensions of the resistor.


 is not necessarily true, as discussed below.
is not necessarily true, as discussed below.





 is the length of the conductor, measured in
is the length of the conductor, measured in  . Resistivity is a measure of the material's ability to oppose electric current.
. Resistivity is a measure of the material's ability to oppose electric current.


 is the
is the  is the
is the 
 for AC circuits, just as
for AC circuits, just as 

 is called the temperature coefficient of resistance,
is called the temperature coefficient of resistance,  is a fixed reference temperature (usually room temperature), and
is a fixed reference temperature (usually room temperature), and  is the resistance at temperature
is the resistance at temperature  , and the relationship only holds in a range of temperatures around the reference.
, and the relationship only holds in a range of temperatures around the reference.