Misplaced Pages

User:DVdm: Difference between revisions

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Browse history interactively← Previous editNext edit →Content deleted Content addedVisualWikitext
Revision as of 14:33, 3 June 2013 view sourceDVdm (talk | contribs)Autopatrolled, Extended confirmed users, New page reviewers, Pending changes reviewers, Rollbackers138,475 editsm →A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive): lighter backgrounds← Previous edit Revision as of 14:41, 3 June 2013 view source DVdm (talk | contribs)Autopatrolled, Extended confirmed users, New page reviewers, Pending changes reviewers, Rollbackers138,475 edits →A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive): Darkened math colour to DarkGreenNext edit →
Line 10: Line 10:
: (start quote) : (start quote)
<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; background-color: {{{color|#fff7f7}}};"> <div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; background-color: {{{color|#fff7f7}}};">
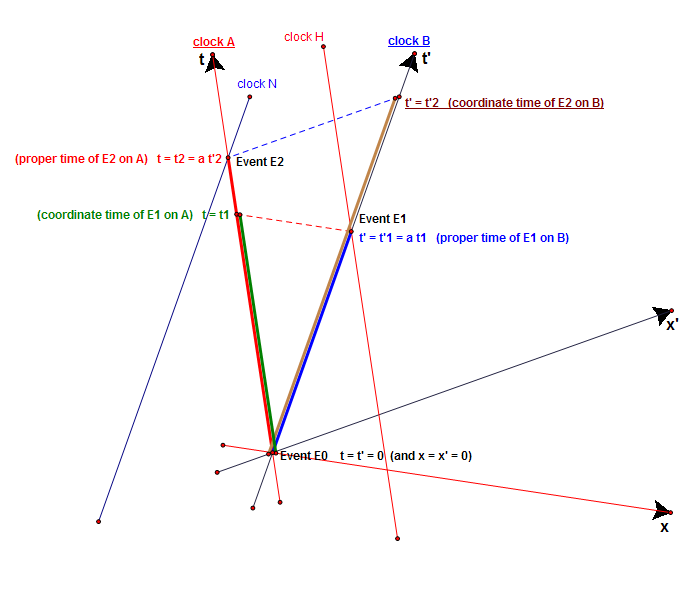
:: {{!xt|Thus, between events E0 and E1, A advances by <math>\color{Green}{t_1}</math> and B by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} :: {{!xt|Thus, between events E0 and E1, A advances by <math>\color{DarkGreen}{t_1}</math> and B by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}}
::: <math>\frac{\color{Green}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{Green}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> ::: <math>\frac{\color{DarkGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{DarkGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math>
:: ... :: ...
:: {{!xt|Thus, between events E0 and E2, B advances by <math>\color{Brown}{t'_2}</math> and A by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}} :: {{!xt|Thus, between events E0 and E2, B advances by <math>\color{Brown}{t'_2}</math> and A by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}}
Line 21: Line 21:
: (start correction) : (start correction)
<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; background-color: {{{color|#f7fff7}}};"> <div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; background-color: {{{color|#f7fff7}}};">
:: {{xt|Thus, between events E0 and E1, A, which is '''not present''' at both events, advances by <math>\color{Green}{t_1}</math> and B, which is '''present''' at both events, by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} :: {{xt|Thus, between events E0 and E1, A, which is '''not present''' at both events, advances by <math>\color{DarkGreen}{t_1}</math> and B, which is '''present''' at both events, by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}}
::: <math>\frac{\color{Green}{\text{rate of clock not present at both events E0 and E1}}}{\color{Blue}{\text{rate of clock present at both events E0 and E1}}} = \frac{\color{Green}{\text{coordinate time of E1}}}{\color{Blue}{\text{proper time of E1}}} = \frac{\color{Green}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{Green}{t_1}}{\color{Blue}{t'_1}} = \frac{\color{Green}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> ::: <math>\frac{\color{DirkGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color{Blue}{\text{rate of clock present at both events E0 and E1}}} = \frac{\color{<<DarkGreen}{\text{coordinate time of E1}}}{\color{Blue}{\text{proper time of E1}}} = \frac{\color{DarkGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{DirkGreen}{t_1}}{\color{Blue}{t'_1}} = \frac{\color{DarkGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math>
:: ... :: ...
:: {{xt|Thus, between events E0 and E2, B, which is '''not present''' at both events, advances by <math>\color{Brown}{t'_2}</math> and A, which is '''present''' at both events, by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}} :: {{xt|Thus, between events E0 and E2, B, which is '''not present''' at both events, advances by <math>\color{Brown}{t'_2}</math> and A, which is '''present''' at both events, by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}}

Revision as of 14:41, 3 June 2013

This...
This user has been on Misplaced Pages for 19 years and 8 months.
This user listens to Frank Zappa.
vn-82This user page has been vandalized 82 times.

A trivial refutation of one of Dingle's Fumbles (Ref: Talk:Herbert Dingle Archive)

On page 230 in this appendix to "Science At the Crossroads", Dingle writes:

(start quote)
Thus, between events E0 and E1, A advances by t 1 {\displaystyle \color {DarkGreen}{t_{1}}} and B by t 1 ′ = a t 1 {\displaystyle \color {Blue}{t'_{1}=at_{1}}} by (1). Therefore
rate of A rate of B = t 1 a t 1 = 1 a > 1 (3) {\displaystyle {\frac {\color {DarkGreen}{\text{rate of A}}}{\color {Blue}{\text{rate of B}}}}={\frac {\color {DarkGreen}{t_{1}}}{\color {Blue}{at_{1}}}}={\frac {1}{a}}>1\qquad {\text{(3)}}}
...
Thus, between events E0 and E2, B advances by t 2 ′ {\displaystyle \color {Brown}{t'_{2}}} and A by t 2 = a t 2 ′ {\displaystyle \color {Red}{t_{2}=at'_{2}}} by (2). Therefore
rate of A rate of B = a t 2 ′ t 2 ′ = a < 1 (4) {\displaystyle {\frac {\color {Red}{\text{rate of A}}}{\color {Brown}{\text{rate of B}}}}={\frac {\color {Red}{at'_{2}}}{\color {Brown}{t'_{2}}}}=a<1\qquad {\text{(4)}}}
Equations (3) and (4) are contradictory: hence the theory requiring them must be false.
(end quote)

Dingle should have written as follows:

(start correction)
Thus, between events E0 and E1, A, which is not present at both events, advances by t 1 {\displaystyle \color {DarkGreen}{t_{1}}} and B, which is present at both events, by t 1 ′ = a t 1 {\displaystyle \color {Blue}{t'_{1}=at_{1}}} by (1). Therefore
Failed to parse (syntax error): {\displaystyle \frac{\color{DirkGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color{Blue}{\text{rate of clock present at both events E0 and E1}}} = \frac{\color{<<DarkGreen}{\text{coordinate time of E1}}}{\color{Blue}{\text{proper time of E1}}} = \frac{\color{DarkGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{DirkGreen}{t_1}}{\color{Blue}{t'_1}} = \frac{\color{DarkGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}}
...
Thus, between events E0 and E2, B, which is not present at both events, advances by t 2 ′ {\displaystyle \color {Brown}{t'_{2}}} and A, which is present at both events, by t 2 = a t 2 ′ {\displaystyle \color {Red}{t_{2}=at'_{2}}} by (2). Therefore
rate of clock not present at both events E0 and E2 rate of clock present at both events E0 and E2 = coordinate time of E2 proper time of E2 = rate of B rate of A = t 2 ′ t 2 = t 2 ′ a t 2 ′ = 1 a > 1 (4) {\displaystyle {\frac {\color {Brown}{\text{rate of clock not present at both events E0 and E2}}}{\color {Red}{\text{rate of clock present at both events E0 and E2}}}}={\frac {\color {Brown}{\text{coordinate time of E2}}}{\color {Red}{\text{proper time of E2}}}}={\frac {\color {Brown}{\text{rate of B}}}{\color {Red}{\text{rate of A}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{t_{2}}}}={\frac {\color {Brown}{t'_{2}}}{\color {Red}{at'_{2}}}}={\frac {1}{a}}>1\qquad {\text{(4)}}}
Equations (3) and (4) are consistent and say that any event's coordinate time is always larger than its proper time:

hence there is no reason to say that the theory requiring them must be false.

(end correction)

DVdm 12:18, 6 August 2007 (UTC)