| Revision as of 09:11, 3 March 2005 edit69.140.58.105 (talk) →Energy← Previous edit | Latest revision as of 16:53, 28 December 2024 edit undoConstant314 (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers13,436 edits Restored revision 1265751023 by 2A00:23C8:9883:A001:45B:C2FF:3319:3165 (talk): This article is about capacitance, not capacitors. The onus for a consensus is on the editor ading the material.Tags: Twinkle Undo | ||
| Line 1: | Line 1: | ||
| {{Short description|Ability of a body to store an electrical charge}} | |||
| '''Capacitance''' is the ability of a ] to store ] or ''voltage'' for a given amount of stored ]. The ] unit of capacitance is the ]. | |||
| {{For|capacitance of blood vessels|Compliance (physiology)}} | |||
| {{Use dmy dates|date=June 2020}} | |||
| {{Infobox physical quantity | |||
| | name = | |||
| | width = | |||
| | background = | |||
| | image = | |||
| | caption = | |||
| | unit = ] | |||
| | otherunits =μF, nF, pF | |||
| | symbols = {{math|''C''}} | |||
| | baseunits = F = A<sup>2</sup> s<sup>4</sup> kg<sup>−1</sup> m<sup>−2</sup> | |||
| | dimension = wikidata | |||
| | derivations = ''C'' = ''']''' / ''']''' | |||
| }} | |||
| {{Electromagnetism |Network}} | |||
| '''Capacitance''' is the ability of an object to store ]. It is measured by the charge in response to a difference in ], expressed as the ratio of those quantities. Commonly recognized are two closely related notions of capacitance: ''self capacitance'' and ''mutual capacitance''.<ref name=Harrington_2003>{{cite book |last=Harrington |first=Roger F. |author-link=Roger F. Harrington |title=Introduction to Electromagnetic Engineering |publisher=Dover Publications |year=2003 |edition=1st |page=43 |isbn=0-486-43241-6}}</ref>{{rp|237–238}} An object that can be electrically charged exhibits self capacitance, for which the electric potential is measured between the object and ground. Mutual capacitance is measured between two components, and is particularly important in the operation of the ], an elementary ] ] designed to add capacitance to an ]. | |||
| The capacitance between two ] depends only on the geometry; the opposing surface area of the conductors and the distance between them; and the ] of any ] material between them. For many dielectric materials, the permittivity, and thus the capacitance, is independent of the potential difference between the conductors and the total charge on them. | |||
| :<math>C = \frac{Q}{V}</math> | |||
| The ] unit of capacitance is the ] (symbol: F), named after the English physicist ].<ref name="NSW" /> A 1 farad capacitor, when charged with 1 ] of electrical charge, has a potential difference of 1 ] between its plates.<ref>{{cite web |url=http://www.collinsdictionary.com/dictionary/english/farad |title=Definition of 'farad' |publisher=Collins}}</ref> The reciprocal of capacitance is called ]. | |||
| ==Self capacitance== | |||
| In discussing electrical circuits, the term ''capacitance'' is usually a shorthand for the mutual capacitance between two adjacent conductors, such as the two plates of a capacitor. However, every isolated conductor also exhibits capacitance, here called ''self capacitance''. It is measured by the amount of electric charge that must be added to an isolated conductor to raise its ] by one unit of measurement, e.g., one ].<ref>{{cite book|author=William D. Greason| title=Electrostatic discharge in electronics|url=https://books.google.com/books?id=404fAQAAIAAJ|year=1992|publisher=Research Studies Press|isbn=978-0-86380-136-5 |page=48}}</ref> The reference point for this potential is a theoretical hollow conducting sphere, of infinite radius, with the conductor centered inside this sphere. | |||
| Self capacitance of a conductor is defined by the ratio of charge and electric potential: | |||
| <math display="block">C = \frac{q}{V},</math> | |||
| where | where | ||
| *<math display="inline">q</math> is the charge held, | |||
| *<big><math display="inline">V = \frac{1}{4\pi\varepsilon_0}\int \frac{\sigma}{r}\,dS</math></big> is the electric potential, | |||
| *<math display="inline">\sigma</math> is the surface charge density, | |||
| *<math display="inline">dS</math> is an infinitesimal element of area on the surface of the conductor, over which the surface charge density is integrated, | |||
| *<math display="inline">r</math> is the length from <math display="inline">dS</math> to a fixed point ''M'' on the conductor, | |||
| *<math>\varepsilon_0</math> is the ]. | |||
| Using this method, the self capacitance of a conducting sphere of radius <math display="inline">R</math> in free space (i.e. far away from any other charge distributions) is:<ref name=NSW>{{cite web|archive-url= https://web.archive.org/web/20090226225105/http://www.phys.unsw.edu.au/COURSES/FIRST_YEAR/pdf%20files/5Capacitanceanddielectr.pdf|archive-date=2009-02-26|url=http://www.phys.unsw.edu.au/COURSES/FIRST_YEAR/pdf%20files/5Capacitanceanddielectr.pdf|title=Lecture notes: Capacitance and Dieletrics|publisher=University of New South Wales}}</ref> | |||
| :''C'' is the capacitance | |||
| <math display="block">C = 4 \pi \varepsilon_0 R.</math> | |||
| Example values of self capacitance are: | |||
| :''Q'' is the charge | |||
| *for the top "plate" of a ], typically a sphere 20 cm in radius: 22.24 pF, | |||
| *the planet ]: about 710 μF.<ref>{{cite book | last1 = Tipler | first1 = Paul | last2 = Mosca | first2 = Gene | title = Physics for Scientists and Engineers | publisher = Macmillan | year = 2004 | edition = 5th | page = 752 | isbn = 978-0-7167-0810-0 }}</ref> | |||
| The inter-winding capacitance of a ] is sometimes called self capacitance,<ref>{{cite journal| title=Self capacitance of inductors|doi=10.1109/63.602562 |last1=Massarini |first1=A. |last2=Kazimierczuk |first2=M. K. |year=1997 |volume=12 |issue=4 |pages=671–676 |journal=IEEE Transactions on Power Electronics |postscript=: example of the use of the term 'self capacitance'.|bibcode=1997ITPE...12..671M |citeseerx=10.1.1.205.7356 }}</ref> but this is a different phenomenon. It is actually mutual capacitance between the individual turns of the coil and is a form of stray or ]. This self capacitance is an important consideration at high frequencies: it changes the ] of the coil and gives rise to parallel ]. In many applications this is an undesirable effect and sets an upper frequency limit for the correct operation of the circuit.{{citation needed|date=May 2017}} | |||
| :''V'' is the potential difference | |||
| ==Mutual capacitance== | |||
| A capacitor has a capacitance of one ] when one ] of charge causes a potential difference of one ] across the capacitor. Since the farad is a very large unit, values of capacitors are usually expressed in microfarads (μF), nanofarads (nF) or picofarads (pF). | |||
| A common form is a parallel-plate ], which consists of two conductive plates insulated from each other, usually sandwiching a ] material. In a parallel plate capacitor, capacitance is very nearly proportional to the surface area of the conductor plates and inversely proportional to the separation distance between the plates. | |||
| If the charges on the plates are <math display="inline">+q</math> and <math display="inline">-q</math>, and <math display="inline">V</math> gives the ] between the plates, then the capacitance <math display="inline">C</math> is given by <math display="block">C = \frac{q}{V},</math> | |||
| The above equation is only accurate for values of Q which are much larger than the ] charge ''e'' = 1.602·10<sup>-19</sup> C. For example, if a capacitance of 1 pF is charged to a voltage of 1 µV, the equation would predict a charge ''Q'' = 10<sup>-19</sup> C, but this is impossible as it is smaller than the charge on a single electron. | |||
| which gives the voltage/] relationship | |||
| <math display="block">i(t) = C \frac{dv(t)}{dt} + V\frac{dC}{dt},</math> | |||
| where <big><math display="inline">\frac{dv(t)}{dt}</math></big> is the instantaneous rate of change of voltage, and <big><math display="inline">\frac{dC}{dt}</math></big> is the instantaneous rate of change of the capacitance. For most applications, the change in capacitance over time is negligible, so the formula reduces to: | |||
| <math display="block">i(t) = C \frac{dv(t)}{dt},</math> | |||
| The energy stored in a capacitor is found by ] the work <math display="inline">W</math>: | |||
| The capacitance of a ''parallel-plate'' capacitor constructed of two identical plane electrodes of area ''A'' at constant spacing ''d'' is approximately equal to the following: | |||
| <math display="block"> W_\text{charging} = \frac{1}{2}CV^2.</math> | |||
| ===Capacitance matrix=== | |||
| where | |||
| The discussion above is limited to the case of two conducting plates, although of arbitrary size and shape. The definition <math>C = Q/V</math> does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case, ] introduced his '']''. If three (nearly ideal) conductors are given charges <math>Q_1, Q_2, Q_3</math>, then the voltage at conductor 1 is given by | |||
| <math display="block">V_1 = P_{11}Q_1 + P_{12} Q_2 + P_{13}Q_3, </math> | |||
| and similarly for the other voltages. ] and ] showed that the coefficients of potential are symmetric, so that <math>P_{12} = P_{21}</math>, etc. Thus the system can be described by a collection of coefficients known as the ''elastance matrix'' or ''reciprocal capacitance matrix'', which is defined as: | |||
| <math display="block">P_{ij} = \frac{\partial V_{i}}{\partial Q_{j}}.</math> | |||
| From this, the mutual capacitance <math>C_{m}</math> between two objects can be defined<ref name=Jackson1999>{{cite book |last=Jackson |first=John David |title=Classical Electrodynamic |publisher=John Wiley & Sons |year=1999 |edition=3rd |page=43 |isbn=978-0-471-30932-1}}</ref> by solving for the total charge <math display="inline">Q</math> and using <math>C_{m}=Q/V</math>. | |||
| :''C'' is the capacitance in farads | |||
| <math display="block">C_m = \frac{1}{(P_{11} + P_{22})-(P_{12} + P_{21})}.</math> | |||
| :'']'' is the electrostatic permittivity of vacuum or free space, measured in farad per metre | |||
| Since no actual device holds perfectly equal and opposite charges on each of the two "plates", it is the mutual capacitance that is reported on capacitors. | |||
| :''ε<sub>r</sub>'' is the ] or relative ] of the insulator used | |||
| The collection of coefficients <math>C_{ij} = \frac{\partial Q_{i}}{\partial V_{j}}</math> is known as the ''capacitance matrix'',<ref name=maxwell>{{cite book| last =Maxwell | first =James | author-link =James Clerk Maxwell | title = A treatise on electricity and magnetism |volume=1 | publisher = Clarendon Press | year = 1873 | chapter =3 | at =p. 88ff | chapter-url = https://archive.org/details/electricandmagne01maxwrich}}</ref><ref>{{Cite web |title=Capacitance: Charge as a Function of Voltage |url=http://www.av8n.com/physics/capacitance.htm |website=Av8n.com |access-date=20 September 2010}}</ref><ref>{{cite journal |last1= Smolić |first1= Ivica |last2= Klajn |first2= Bruno |date= 2021 |title= Capacitance matrix revisited |url= https://www.jpier.org/PIERB/pier.php?paper=21011501 |journal= Progress in Electromagnetics Research B |volume= 92 |pages= 1–18 |doi= 10.2528/PIERB21011501|arxiv=2007.10251 |access-date= 4 May 2021|doi-access= free }}</ref> and is the ] of the elastance matrix. | |||
| :''A'' is the area of each plane electrode, measured in ]s | |||
| ==Capacitors== | |||
| :''d'' is the separation between the electrodes, measured in metres | |||
| {{Main|Capacitor}} | |||
| The capacitance of the majority of capacitors used in electronic circuits is generally several orders of magnitude smaller than the ]. The most common units of capacitance are the ]farad (μF), ]farad (nF), ]farad (pF), and, in microcircuits, ]farad (fF). Some applications also use ] that can be much larger, as much as hundreds of farads, and parasitic capacitive elements can be less than a femtofarad. Historical texts use other, obsolete submultiples of the farad, such as "mf" and "mfd" for microfarad (μF); "mmf", "mmfd", "pfd", "μμF" for picofarad (pF).<ref>{{cite web |url=http://www.justradios.com/MFMMFD.html |title=Capacitor MF-MMFD Conversion Chart |website=Just Radios}}</ref><ref>{{cite book |url=https://archive.org/details/FundamentalsOfElectronics93400A1b |title=Fundamentals of Electronics |volume=1b – Basic Electricity – Alternating Current |publisher=Bureau of Naval Personnel |year=1965 |page=}}</ref> | |||
| The capacitance can be calculated if the geometry of the conductors and the dielectric properties of the insulator between the conductors are known. Capacitance is proportional to the area of overlap and inversely proportional to the separation between conducting sheets. The closer the sheets are to each other, the greater the capacitance. | |||
| === Energy === | |||
| An example is the capacitance of a capacitor constructed of two parallel plates both of area <math display="inline">A</math> separated by a distance <math display="inline">d</math>. If <math display="inline">d</math> is sufficiently small with respect to the smallest chord of <math display="inline">A</math>, there holds, to a high level of accuracy: | |||
| The ] (measured in ]s) stored in a capacitor is equal to the ''work'' done to charge it up. Consider a capacitor with capacitance ''C'', holding a charge ''+q'' on one plate and ''-q'' on the other. Moving a small element of charge ''dq'' from one plate to the other against the potential difference ''V = q/C'' requires the work ''dW'': | |||
| <math display="block">\ C=\varepsilon\frac{A}{d};</math> | |||
| <math display="block">\varepsilon=\varepsilon_0 \varepsilon_r,</math> | |||
| where | where | ||
| *<math display="inline">C</math> is the capacitance, in farads; | |||
| *<math display="inline">A</math> is the area of overlap of the two plates, in square meters; | |||
| *<math display="inline">\varepsilon_0</math> is the ] {{nowrap|(<math display="inline">\varepsilon_0 \approx 8.854\times 10^{-12} ~ \mathrm{F{\cdot}m^{-1}}</math>);}} | |||
| *<math display="inline">\varepsilon_r</math> is the ] (also dielectric constant) of the material in between the plates {{nowrap|(<math display="inline">\varepsilon_r \approx 1</math>}} for air); and | |||
| *<math display="inline">d</math> is the separation between the plates, in meters. | |||
| The equation is a good approximation if ''d'' is small compared to the other dimensions of the plates so that the electric field in the capacitor area is uniform, and the so-called ''fringing field'' around the periphery provides only a small contribution to the capacitance. | |||
| :''W'' is the work measured in ]s | |||
| Combining the equation for capacitance with the above equation for the energy stored in a capacitor, for a flat-plate capacitor the energy stored is: | |||
| :''q'' is the charge measured in ]s | |||
| <math display="block"> W_\text{stored} = \frac{1}{2} C V^2 = \frac{1}{2} \varepsilon \frac{A}{d} V^2.</math> | |||
| where <math display="inline">W</math> is the energy, in joules; <math display="inline">C</math> is the capacitance, in farads; and <math display="inline">V</math> is the voltage, in volts. | |||
| ==Stray capacitance== | |||
| {{Main|Parasitic capacitance}} | |||
| Any two adjacent conductors can function as a capacitor, though the capacitance is small unless the conductors are close together for long distances or over a large area. This (often unwanted) capacitance is called parasitic or stray capacitance. Stray capacitance can allow signals to leak between otherwise isolated circuits (an effect called ]), and it can be a limiting factor for proper functioning of circuits at ]. | |||
| Stray capacitance between the input and output in amplifier circuits can be troublesome because it can form a path for ], which can cause instability and ] in the amplifier. It is often convenient for analytical purposes to replace this capacitance with a combination of one input-to-ground capacitance and one output-to-ground capacitance; the original configuration – including the input-to-output capacitance – is often referred to as a pi-configuration. Miller's theorem can be used to effect this replacement: it states that, if the gain ratio of two nodes is {{sfrac|1|''K''}}, then an ] of ''Z'' connecting the two nodes can be replaced with a {{sfrac|''Z''|1 − ''K''}} impedance between the first node and ground and a {{sfrac|''KZ''|''K'' − 1}} impedance between the second node and ground. Since impedance varies inversely with capacitance, the internode capacitance, ''C'', is replaced by a capacitance of KC from input to ground and a capacitance of {{sfrac|(''K'' − 1)''C''|''K''}} from output to ground. When the input-to-output gain is very large, the equivalent input-to-ground impedance is very small while the output-to-ground impedance is essentially equal to the original (input-to-output) impedance. | |||
| We can find the energy stored in a capacitor by ] this equation. Starting with an uncharged capacitor (''q=0'') and moving charge from one plate to the other until the plates have charge ''+Q'' and ''-Q'' requires the work ''W'': | |||
| ==Capacitance of conductors with simple shapes == | |||
| :<math> W_{charging} = \int_{0}^{Q} \frac{q}{C} dq = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}CV^2 = W_{stored}</math> | |||
| Calculating the capacitance of a system amounts to solving the ] <math display="inline">\nabla^2\varphi=0</math> with a constant potential <math display="inline">\varphi</math> on the 2-dimensional surface of the conductors embedded in 3-space. This is simplified by symmetries. There is no solution in terms of elementary functions in more complicated cases. | |||
| For plane situations, analytic functions may be used to map different geometries to each other. See also ]. | |||
| Combining this with the above equation for the capacitance of a flat-plate capacitor, we get: | |||
| {| class="wikitable" | |||
| :<math> W_{stored} = \frac{1}{2} \epsilon_0 \epsilon_r \frac{A}{d} V^2</math> epsilon= 8.85 times ten to the negative 12th | |||
| |+ Capacitance of simple systems | |||
| ! Type !! Capacitance !! Diagram and definitions | |||
| |- | |||
| ! Parallel-plate capacitor | |||
| | <math>\ \mathcal{C} = \frac{\ \varepsilon A\ }{d}\ </math> | |||
| | ] | |||
| *<math display="inline">\varepsilon</math>: ] | |||
| |- | |||
| ! Concentric cylinders | |||
| | <math>\ \mathcal{C} = \frac{2\pi \varepsilon \ell}{\ \ln \left( R_{2}/R_{1}\right)\ }\ </math> | |||
| | ] | |||
| *<math display="inline">\varepsilon</math>: ] | |||
| |- | |||
| ! Eccentric cylinders<ref>{{cite journal |last=Dawes |year=1973 |first=Chester L. |title=Capacitance and potential gradients of eccentric cylindrical condensers |doi=10.1063/1.1745162 |journal=Physics |volume=4 |issue=2 |pages=81–85 |url=https://aip.scitation.org/doi/abs/10.1063/1.1745162}}</ref> | |||
| | <big><math>\ \mathcal{C} = \frac{2\pi \varepsilon \ell}{\ \operatorname{arcosh}\left(\frac{R_{1}^2 + R_{2}^2 - d^2}{2 R_{1} R_{2}}\right)\ }\ </math></big> | |||
| | ] | |||
| *<math display="inline">\varepsilon</math>: ] | |||
| *<math display="inline">R_1</math>: Outer radius | |||
| *<math display="inline">R_2</math>: Inner radius | |||
| *<math display="inline">d</math>: Distance between center | |||
| *<math display="inline">\ell</math>: Wire length | |||
| |- | |||
| ! Pair of parallel wires<ref name="Jackson 1975 80">{{cite book |last=Jackson |first=J. D. |year=1975 |title=Classical Electrodynamics |publisher=Wiley |page=80}}</ref> | |||
| | <big><math>\ \mathcal{C} = \frac{\pi \varepsilon \ell}{\ \operatorname{arcosh}\left( \frac{d}{2a}\right)\ } = \frac{\pi \varepsilon \ell}{\ \ln \left( \frac{d}{\ 2a\ } + \sqrt{\frac{d^2}{\ 4a^2\ } -1\ }\right)\ }\ </math></big> | |||
| |] | |||
| |- | |||
| ! Wire parallel to wall<ref name="Jackson 1975 80"/> | |||
| | <big><math>\ \mathcal{C} = \frac{2\pi \varepsilon \ell}{\ \operatorname{arcosh}\left( \frac{d}{a}\right)\ } = \frac{2\pi \varepsilon \ell}{\ \ln \left( \frac{\ d\ }{a}+\sqrt{\frac{\ d^2\ }{a^2} - 1\ }\right)\ }\ </math></big> | |||
| | | |||
| *<math display="inline">a</math>: Wire radius | |||
| *<math display="inline">d</math>: Distance, <math display="inline">d > a</math> | |||
| *<math display="inline">\ell</math>: Wire length | |||
| |- | |||
| ! Two parallel<br/>coplanar strips<ref>{{cite book | last1 = Binns | last2 = Lawrenson | year = 1973 | title = Analysis and computation of electric and magnetic field problems | publisher = Pergamon Press | isbn = 978-0-08-016638-4}}<!--| access-date = 4 June 2010 --></ref> | |||
| | <math>\ \mathcal{C} = \varepsilon \ell\ \frac{\ K\left( \sqrt{1-k^2\ } \right)\ }{ K\left( k \right) }\ </math> | |||
| | | |||
| *<math display="inline">d</math>: Distance | |||
| *<math display="inline">\ell</math>: Length | |||
| *<math display="inline">w_1, w_2</math>: Strip width | |||
| *<math display="inline">\ k_1 = \left( \tfrac{\ 2 w_1\ }{d} + 1 \right)^{-1}\ </math><br/><math>\ k_2 = \left( \tfrac{\ 2 w_2\ }{d} + 1 \right)^{-1}\ </math><math>\ k = \sqrt{ k_1\ k_2\ }\ </math> | |||
| *<math display="inline">K</math>: ] | |||
| |- | |||
| ! Concentric spheres | |||
| | <math>\ \mathcal{C} = \frac{4\pi \varepsilon}{\ \frac{1}{R_1} - \frac{1}{R_2}\ }\ </math> | |||
| | ] | |||
| *<math display="inline">\varepsilon</math>: ] | |||
| |- | |||
| ! Two spheres,<br/>equal radius<ref name="Maxwell 1873 266 ff">{{Cite book |last=Maxwell |first=J.;C. |year=1873 |title=A Treatise on Electricity and Magnetism |publisher=Dover |page=266 ff |isbn=978-0-486-60637-8}}</ref><ref>{{Cite journal |last=Rawlins |first=A.D. |year=1985 |title=Note on the capacitance of two closely separated spheres |journal=IMA Journal of Applied Mathematics |volume=34 |issue=1 |pages=119–120 |doi=10.1093/imamat/34.1.119}}</ref> | |||
| | <math>\begin{align} | |||
| \ \mathcal{C}\ = &\ {} 2 \pi \varepsilon a\ \sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^2-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^2-1}\right) \right) } \\ | |||
| ={}&{}2\pi \varepsilon a\left \\ | |||
| ={}&{} 2\pi \varepsilon a\left \\ | |||
| ={}&{} 2\pi \varepsilon a \,\frac{\sqrt{D^2 - 1}}{\log(q)}\left | |||
| \end{align}\ </math> | |||
| | | |||
| *<math display="inline">a</math>: Radius | |||
| *<math display="inline">d</math>: Distance, <math display="inline">d > 2a</math> | |||
| *<math display="inline">D = d/2a, D > 1</math> | |||
| *<math display="inline">\gamma</math>: ] | |||
| *<math>q = D + \sqrt{D^2 - 1}</math> | |||
| *<math>\psi_q(z)=\frac{\partial_z\Gamma_q(z)}{\Gamma_q(z)}</math>: the q-digamma function | |||
| *<math>\Gamma_q(z)</math>: the ]<ref>{{Cite book| last1 = Gasper | last2 = Rahman | title = Basic Hypergeometric Series | year = 2004 | publisher = Cambridge University Press |at = p.20-22 | isbn = 978-0-521-83357-8}}</ref> | |||
| See also ]. | |||
| |- | |||
| ! Sphere in front of wall<ref name="Maxwell 1873 266 ff"/> | |||
| | <math>\ \mathcal{C} = 4\pi \varepsilon a\sum_{n=1}^{\infty }\frac{\sinh \left( \ln \left( D+\sqrt{D^{2}-1}\right) \right) }{\sinh \left( n\ln \left( D+\sqrt{ D^{2}-1}\right) \right) }\ </math> | |||
| | | |||
| *<math>\ a\ </math>: Radius | |||
| *<math>\ d\ </math>: Distance, <math>d > a</math> | |||
| *<math>D=d/a</math> | |||
| |- | |||
| ! Sphere | |||
| | <math>\ \mathcal{C} = 4 \pi \varepsilon a\ </math> | |||
| | | |||
| *<math>a</math>: Radius | |||
| |- | |||
| ! Circular disc<ref name="Jackson 1975 128">{{cite book |last=Jackson |first=J.D. |year=1975 |title=Classical Electrodynamics |publisher=Wiley |page=128, problem 3.3 }}</ref> | |||
| | <math>\ \mathcal{C} = 8 \varepsilon a\ </math> | |||
| | | |||
| * <math>a</math>: Radius | |||
| |- | |||
| ! Thin straight wire,<br/> finite length<ref>{{cite journal |last=Maxwell |first=J. C. |year=1878 |title=On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness |journal=Proceedings of the London Mathematical Society |volume=IX |pages=94–101 |doi=10.1112/plms/s1-9.1.94 |url=https://zenodo.org/record/1447764 }}</ref><ref>{{Cite journal |last=Vainshtein |first=L. A. |year=1962 |title=Static boundary problems for a hollow cylinder of finite length. III Approximate formulas |journal=] |volume=32 |pages=1165–1173}}</ref><ref>{{cite journal |last=Jackson |first=J. D. |year=2000 |title=Charge density on thin straight wire, revisited |journal=American Journal of Physics |volume=68 |issue=9 |pages=789–799 |doi=10.1119/1.1302908 |bibcode = 2000AmJPh..68..789J }}</ref> | |||
| | <math>\ \mathcal{C} = \frac{2\pi \varepsilon \ell}{\Lambda }\left\ </math> | |||
| | | |||
| *<math>a</math>: Wire radius | |||
| *<math>\ell</math>: Length | |||
| *<math>\ \Lambda = \ln \left( \ell/a \right)\ </math> | |||
| |} | |||
| ==Energy storage== | |||
| If the maximum voltage a capacitor can withstand is <math>V_{max} \,</math> (equal to <math>E_{str}d \,</math> where <math>E_{str} \,</math> is the dielectric strength), then the maximum energy it can store is: | |||
| The ] (measured in ]s) stored in a capacitor is equal to the ''work'' required to push the charges into the capacitor, i.e. to charge it. Consider a capacitor of capacitance ''C'', holding a charge +''q'' on one plate and −''q'' on the other. Moving a small element of charge d''q'' from one plate to the other against the potential difference {{nowrap|1=''V'' = ''q''/''C''}} requires the work d''W'': | |||
| <math display="block"> \mathrm{d}W = \frac{q}{C}\,\mathrm{d}q,</math> | |||
| where ''W'' is the work measured in joules, ''q'' is the charge measured in coulombs and ''C'' is the capacitance, measured in farads. | |||
| The energy stored in a capacitor is found by ] this equation. Starting with an uncharged capacitance ({{nowrap|1=''q'' = 0}}) and moving charge from one plate to the other until the plates have charge +''Q'' and −''Q'' requires the work ''W'': | |||
| :<math> W_{max} = \frac{1}{2} \epsilon_0 \epsilon_r E_{str}^2 A d</math> | |||
| <math display="block"> W_\text{charging} = \int_0^Q \frac{q}{C} \, \mathrm{d}q = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}QV = \frac{1}{2}CV^2 = W_\text{stored}.</math> | |||
| ==Nanoscale systems== | |||
| In the design of a capacitor, the main variables are the choice of dielectric, and the "plate" dimensions. The selection of dielectric determines the relative permittivity and breakdown strength, and hence the energy capacity per unit volume of dielectric. | |||
| The capacitance of nanoscale dielectric capacitors such as ] may differ from conventional formulations of larger capacitors. In particular, the electrostatic potential difference experienced by electrons in conventional capacitors is spatially well-defined and fixed by the shape and size of metallic electrodes in addition to the statistically large number of electrons present in conventional capacitors. In nanoscale capacitors, however, the electrostatic potentials experienced by electrons are determined by the number and locations of all electrons that contribute to the electronic properties of the device. In such devices, the number of electrons may be very small, so the resulting spatial distribution of equipotential surfaces within the device is exceedingly complex. | |||
| ===Single-electron devices=== | |||
| === In electric circuits === | |||
| The capacitance of a connected, or "closed", single-electron device is twice the capacitance of an unconnected, or "open", single-electron device.<ref name= Tsu>{{Cite book | pages=312–315 | title=Superlattice to Nanoelectronics | isbn = 978-0-08-096813-1 | author=Raphael Tsu | publisher=Elsevier | year=2011 }}</ref> This fact may be traced more fundamentally to the energy stored in the single-electron device whose "direct polarization" interaction energy may be equally divided into the interaction of the electron with the polarized charge on the device itself due to the presence of the electron and the amount of potential energy required to form the polarized charge on the device (the interaction of charges in the device's dielectric material with the potential due to the electron).<ref name= LaFave-DCD>{{Cite journal | author=T. LaFave Jr. | title=Discrete charge dielectric model of electrostatic energy | arxiv=1203.3798|journal=J. Electrostatics | year=2011 | volume=69 | issue=6 | pages=414–418 | doi=10.1016/j.elstat.2011.06.006 | s2cid=94822190 }}</ref> | |||
| ===Few-electron devices=== | |||
| Electrons cannot directly pass across the dielectric from one plate of the capacitor to the other. When a voltage is applied to a capacitor through an external circuit, current flows to one plate, charging it, while flowing away from the other plate, charging it oppositely. In other words, when the voltage across a capacitor changes, the capacitor will be charged or discharged. The associated ] is given by | |||
| The derivation of a "quantum capacitance" of a few-electron device involves the thermodynamic chemical potential of an ''N''-particle system given by | |||
| <math display="block">\mu(N) = U(N) - U(N-1),</math> | |||
| whose energy terms may be obtained as solutions of the Schrödinger equation. The definition of capacitance, | |||
| :<math>I = \frac{dQ}{dt} = C\frac{dV}{dt}</math> | |||
| <math display="block">{1\over C} \equiv {\Delta V\over\Delta Q},</math> | |||
| with the potential difference | |||
| <math display="block">\Delta V = {\Delta \mu \,\over e} = {\mu(N + \Delta N) -\mu(N) \over e}</math> | |||
| may be applied to the device with the addition or removal of individual electrons, | |||
| where | |||
| <math display="block">\Delta N = 1</math> and <math display="block">\Delta Q = e.</math> | |||
| The "quantum capacitance" of the device is then<ref>{{cite journal | |||
| :I is the current flowing in the conventional direction, measured in ]s | |||
| |author1=G. J. Iafrate |author2=K. Hess |author3=J. B. Krieger |author4=M. Macucci |year=1995 | |||
| |title=Capacitive nature of atomic-sized structures | |||
| |journal=Phys. Rev. B | |||
| |volume=52 | |||
| |issue=15 | |||
| |pages=10737–10739 |doi=10.1103/physrevb.52.10737 | |||
| |pmid=9980157 |bibcode = 1995PhRvB..5210737I }}</ref> | |||
| <math display="block">C_Q(N) = \frac{e^2}{\mu(N+1)-\mu(N)} = \frac{e^2}{E(N)}.</math> | |||
| This expression of "quantum capacitance" may be written as | |||
| :dV/dt is the time ] of voltage, measured in ]s / ]. | |||
| <math display="block">C_Q(N) = {e^2\over U(N)},</math> | |||
| which differs from the conventional expression described in the introduction where <math>W_\text{stored} = U</math>, the stored electrostatic potential energy, | |||
| <math display="block">C = {Q^2\over 2U},</math> | |||
| by a factor of {{sfrac|2}} with <math>Q = Ne</math>. | |||
| However, within the framework of purely classical electrostatic interactions, the appearance of the factor of {{sfrac|2}} is the result of integration in the conventional formulation involving the work done when charging a capacitor, | |||
| In the case of a constant voltage (DC), an equilibrium is soon reached, where the charge of the plates corresponds with the applied voltage by the relation ''Q=CV'', and no further current will flow in the circuit. Therefore ] cannot pass. However, effectively ] (AC) can: every change of the voltage gives rise to a further charging or a discharging of the plates and therefore a current. The amount of "resistance" of a capacitor to AC is known as '''capacitive reactance''', and varies depending on the AC frequency. Capacitive reactance is given by this formula: | |||
| <math display="block"> W_\text{charging} = U = \int_0^Q \frac{q}{C} \, \mathrm{d}q,</math> | |||
| which is appropriate since <math>\mathrm{d}q = 0</math> for systems involving either many electrons or metallic electrodes, but in few-electron systems, <math>\mathrm{d}q \to \Delta \,Q= e</math>. The integral generally becomes a summation. One may trivially combine the expressions of capacitance | |||
| :<math>X_C = \frac{1}{2 \pi f C}</math> | |||
| <math display="block">Q=CV</math> | |||
| and electrostatic interaction energy, | |||
| <math display="block">U = Q V ,</math> | |||
| to obtain | |||
| <math display="block">C = Q{1\over V} = Q {Q \over U} = {Q^2 \over U},</math> | |||
| which is similar to the quantum capacitance. A more rigorous derivation is reported in the literature.<ref>{{cite journal | |||
| where | |||
| |author1 = T. LaFave Jr | |||
| |author2 = R. Tsu | |||
| |date = March–April 2008 | |||
| |title = Capacitance: A property of nanoscale materials based on spatial symmetry of discrete electrons | |||
| |url = http://www.pagesofmind.com/FullTextPubs/La08-LaFave-2008-capacitance-a-property-of-nanoscale-materials.pdf | |||
| |access-date = 12 February 2014 | |||
| |journal = Microelectronics Journal | |||
| |volume = 39 | |||
| |issue = 3–4 | |||
| |pages = 617–623 | |||
| |doi = 10.1016/j.mejo.2007.07.105 | |||
| |url-status = dead | |||
| |archive-url = https://web.archive.org/web/20140222131652/http://www.pagesofmind.com/FullTextPubs/La08-LaFave-2008-capacitance-a-property-of-nanoscale-materials.pdf | archive-date = 22 February 2014}}</ref> In particular, to circumvent the mathematical challenges of spatially complex equipotential surfaces within the device, an ''average'' electrostatic potential experienced by each electron is utilized in the derivation. | |||
| Apparent mathematical differences may be understood more fundamentally. The potential energy, <math>U(N)</math>, of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit <math>N = 1</math>. As <math>N</math> grows large, <math>U(N)\to U</math>.<ref name=LaFave-DCD/> Thus, the general expression of capacitance is | |||
| :''X<sub>C</sub>'' = capacitive ], measured in ohms | |||
| <math display="block">C(N) = {(Ne)^2 \over U(N)}.</math> | |||
| In nanoscale devices such as quantum dots, the "capacitor" is often an isolated or partially isolated component within the device. The primary differences between nanoscale capacitors and macroscopic (conventional) capacitors are the number of excess electrons (charge carriers, or electrons, that contribute to the device's electronic behavior) and the shape and size of metallic electrodes. In nanoscale devices, ] consisting of metal atoms typically do not exhibit the same conductive properties as their macroscopic, or bulk material, counterparts. | |||
| :''f'' = ] of AC in ] | |||
| ==Capacitance in electronic and semiconductor devices== | |||
| :''C'' = capacitance in farads | |||
| In electronic and semiconductor devices, transient or frequency-dependent current between terminals contains both conduction and displacement components. Conduction current is related to moving charge carriers (electrons, holes, ions, etc.), while displacement current is caused by a time-varying electric field. Carrier transport is affected by electric fields and by a number of physical phenomena - such as carrier drift and diffusion, trapping, injection, contact-related effects, impact ionization, etc. As a result, device ] is frequency-dependent, and a simple electrostatic formula for capacitance <math>C = q/V,</math> is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is:<ref name=LauxCapacitance>{{cite journal |first=S.E. |last=Laux |title=Techniques for small-signal analysis of semiconductor devices |journal=IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems |volume=4 |issue=4 |pages=472–481 |doi=10.1109/TCAD.1985.1270145 |date=Oct 1985|s2cid=13058472 }}</ref> | |||
| Thus the reactance is ] to the frequency. Since DC has a frequency of zero, the formula confirms that capacitors completely block direct current. For high-frequency alternating currents the reactance is small enough to be considered as zero in approximate analyses. | |||
| <math display="block">C = \frac{\operatorname{Im}(Y(\omega))}{\omega} ,</math> | |||
| where <math>Y(\omega)</math> is the device admittance, and <math>\omega</math> is the angular frequency. | |||
| In general, capacitance is a function of frequency. At high frequencies, capacitance approaches a constant value, equal to "geometric" capacitance, determined by the terminals' geometry and dielectric content in the device. | |||
| Reactance is so called because the capacitor doesn't dissipate power, but merely stores energy. In electrical circuits, as in mechanics, there are two types of load, resistive and reactive. Resistive loads (analogous to an object sliding on a rough surface) dissipate energy that enters them, ultimately by ] emission (see ]), while reactive loads (analogous to a spring or frictionless moving object) retain the energy. | |||
| A paper by Steven Laux<ref name=LauxCapacitance /> presents a review of numerical techniques for capacitance calculation. In particular, capacitance can be calculated by a Fourier transform of a transient current in response to a step-like voltage excitation: | |||
| <math display="block">C(\omega) = \frac{1}{\Delta V} \int_0^\infty \cos (\omega t) dt.</math> | |||
| ==Negative capacitance in semiconductor devices== | |||
| The ] of a capacitor is given by: | |||
| :<math>Z = \frac{-j}{2 \pi f C} = {1 \over j 2 \pi f C}</math> | |||
| Usually, capacitance in semiconductor devices is positive. However, in some devices and under certain conditions (temperature, applied voltages, frequency, etc.), capacitance can become negative. Non-monotonic behavior of the transient current in response to a step-like excitation has been proposed as the mechanism of negative capacitance.<ref name=JonscherNegCap>{{cite journal |first=A.K. |last=Jonscher |title=The physical origin of negative capacitance |journal=J. Chem. Soc. Faraday Trans. II |volume=82 |pages=75–81 |doi=10.1039/F29868200075 |date=1986}}</ref> Negative capacitance has been demonstrated and explored in many different types of semiconductor devices.<ref>{{cite journal |first1=M. |last1=Ershov |first2=H.C. |last2=Liu |first3=L. |last3=Li |first4=M. |last4=Buchanan |first5=Z.R. |last5=Wasilewski |first6=A.K. |last6=Jonscher |title=Negative capacitance effect in semiconductor devices |journal=IEEE Trans. Electron Devices |volume=45 |issue=10 |pages=2196–2206 |date=Oct 1998 |doi=10.1109/16.725254|arxiv=cond-mat/9806145 |bibcode=1998ITED...45.2196E |s2cid=204925581 }}</ref> | |||
| where | |||
| == Measuring capacitance == | |||
| :''j'' is the ] = <math>\sqrt{-1}</math> | |||
| {{Main|Capacitance meter}} | |||
| A ] is a piece of ] used to measure capacitance, mainly of discrete ]s. For most purposes and in most cases the capacitor must be disconnected from ]. | |||
| Many DVMs (]s) have a capacitance-measuring function. These usually operate by charging and discharging the ] with a known ] and measuring the rate of rise of the resulting ]; the slower the rate of rise, the larger the capacitance. DVMs can usually measure capacitance from ] to a few hundred microfarads, but wider ranges are not unusual. It is also possible to measure capacitance by passing a known ] ] through the device under test and measuring the resulting ]age across it (does not work for polarised capacitors). | |||
| Hence, capacitive reactance is the negative imaginary component of impedance. The negative sign indicates that the current leads the voltage by 90° for a sinusoidal signal, as opposed to the inductor, where the current lags the voltage by 90°. | |||
| 2700A capacitance bridge]] | |||
| Also significant is that the impedance is inversely proportional to the capacitance, unlike resistors and inductors for which impedances are linearly proportional to resistance and inductance respectively. This is why the series and shunt impedance formulae (given below) are the inverse of the resistive case. In series, impedances sum. In shunt, conductances sum. | |||
| More sophisticated instruments use other techniques such as inserting the capacitor-under-test into a ]. By varying the values of the other legs in the bridge (so as to bring the bridge into balance), the value of the unknown capacitor is determined. This method of ''indirect'' use of measuring capacitance ensures greater precision. Through the use of ]s and other careful design techniques, these instruments can usually measure capacitors over a range from picofarads to farads. | |||
| In a ] such as a ], the ] selected is a function of the inductance (L) and the capacitance (C) in series, and is given by | |||
| :<math>f = \frac{1}{2 \pi \sqrt{LC}}</math> | |||
| ==See also== | |||
| This is the frequency at which ] occurs in an ]. | |||
| {{div col begin|colwidth=14em}} | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| {{div col end}} | |||
| ==References== | |||
| === Capacitor networks === | |||
| {{reflist|25em}} | |||
| ==Further reading== | |||
| Capacitors in a ] configuration each have the same potential difference (voltage). To find their total equivalent capacitance (''C<sub>eq</sub>''): | |||
| {{Refbegin}} | |||
| *Tipler, Paul (1998). ''Physics for Scientists and Engineers: Vol. 2: Electricity and Magnetism, Light'' (4th ed.). W. H. Freeman. {{ISBN|1-57259-492-6}} | |||
| *Serway, Raymond; Jewett, John (2003). ''Physics for Scientists and Engineers'' (6th ed.). Brooks Cole. {{ISBN|0-534-40842-7}} | |||
| *Saslow, Wayne M.(2002). ''Electricity, Magnetism, and Light''. Thomson Learning. {{ISBN|0-12-619455-6}}. See Chapter 8, and especially pp. 255–259 for coefficients of potential. | |||
| {{Refend}} | |||
| ==External links== | |||
| :] | |||
| *{{Commonscatinline|Capacitance}} | |||
| {{Authority control}} | |||
| :<math> C_{eq} = C_1 + C_2 + \cdots + C_n \,</math> | |||
| ] | |||
| The current through capacitors in ] stays the same, but the voltage across each capacitor can be different. The sum of the potential differences (voltage) is equal to the total voltage. To find their total capacitance: | |||
| ] | |||
| :] | |||
| :<math> \frac{1}{C_{eq}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}</math> | |||
| One possible reason to connect capacitors in series is to increase the overall voltage rating. In practice, a very large resistor might be connected across each capacitor to divide the total voltage appropriately for the individual ratings. | |||
| === Capacitor/inductor duality === | |||
| In mathematical terms, the ideal capacitor can be considered as an inverse of the ideal ], because the voltage-current equations of the two devices can be transformed into one another by exchanging the voltage and current terms. | |||
| Just as two or more inductors can be magnetically coupled to make a ], two or more charged conductors can be electrostatically coupled to make a capacitor. The ''mutual capacitance'' of two conductors is defined as the current that flows in one when the voltage across the other changes by unit voltage in unit time. | |||
| ==See also== | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] | |||
| *] (thought by some to be a capacitor) | |||
| ] | |||
| ] | ] | ||
| ] | |||
| ] | |||
Latest revision as of 16:53, 28 December 2024
Ability of a body to store an electrical charge For capacitance of blood vessels, see Compliance (physiology).
| Common symbols | C |
|---|---|
| SI unit | farad |
| Other units | μF, nF, pF |
| In SI base units | F = A s kg m |
| Derivations from other quantities | C = charge / voltage |
| Dimension |
Capacitance is the ability of an object to store electric charge. It is measured by the charge in response to a difference in electric potential, expressed as the ratio of those quantities. Commonly recognized are two closely related notions of capacitance: self capacitance and mutual capacitance. An object that can be electrically charged exhibits self capacitance, for which the electric potential is measured between the object and ground. Mutual capacitance is measured between two components, and is particularly important in the operation of the capacitor, an elementary linear electronic component designed to add capacitance to an electric circuit.
The capacitance between two conductors depends only on the geometry; the opposing surface area of the conductors and the distance between them; and the permittivity of any dielectric material between them. For many dielectric materials, the permittivity, and thus the capacitance, is independent of the potential difference between the conductors and the total charge on them.
The SI unit of capacitance is the farad (symbol: F), named after the English physicist Michael Faraday. A 1 farad capacitor, when charged with 1 coulomb of electrical charge, has a potential difference of 1 volt between its plates. The reciprocal of capacitance is called elastance.
Self capacitance
In discussing electrical circuits, the term capacitance is usually a shorthand for the mutual capacitance between two adjacent conductors, such as the two plates of a capacitor. However, every isolated conductor also exhibits capacitance, here called self capacitance. It is measured by the amount of electric charge that must be added to an isolated conductor to raise its electric potential by one unit of measurement, e.g., one volt. The reference point for this potential is a theoretical hollow conducting sphere, of infinite radius, with the conductor centered inside this sphere.
Self capacitance of a conductor is defined by the ratio of charge and electric potential: where
- is the charge held,
- is the electric potential,
- is the surface charge density,
- is an infinitesimal element of area on the surface of the conductor, over which the surface charge density is integrated,
- is the length from to a fixed point M on the conductor,
- is the vacuum permittivity.
Using this method, the self capacitance of a conducting sphere of radius in free space (i.e. far away from any other charge distributions) is:
Example values of self capacitance are:
- for the top "plate" of a van de Graaff generator, typically a sphere 20 cm in radius: 22.24 pF,
- the planet Earth: about 710 μF.
The inter-winding capacitance of a coil is sometimes called self capacitance, but this is a different phenomenon. It is actually mutual capacitance between the individual turns of the coil and is a form of stray or parasitic capacitance. This self capacitance is an important consideration at high frequencies: it changes the impedance of the coil and gives rise to parallel resonance. In many applications this is an undesirable effect and sets an upper frequency limit for the correct operation of the circuit.
Mutual capacitance
A common form is a parallel-plate capacitor, which consists of two conductive plates insulated from each other, usually sandwiching a dielectric material. In a parallel plate capacitor, capacitance is very nearly proportional to the surface area of the conductor plates and inversely proportional to the separation distance between the plates.
If the charges on the plates are and , and gives the voltage between the plates, then the capacitance is given by which gives the voltage/current relationship where is the instantaneous rate of change of voltage, and is the instantaneous rate of change of the capacitance. For most applications, the change in capacitance over time is negligible, so the formula reduces to:
The energy stored in a capacitor is found by integrating the work :
Capacitance matrix
The discussion above is limited to the case of two conducting plates, although of arbitrary size and shape. The definition does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case, James Clerk Maxwell introduced his coefficients of potential. If three (nearly ideal) conductors are given charges , then the voltage at conductor 1 is given by and similarly for the other voltages. Hermann von Helmholtz and Sir William Thomson showed that the coefficients of potential are symmetric, so that , etc. Thus the system can be described by a collection of coefficients known as the elastance matrix or reciprocal capacitance matrix, which is defined as:
From this, the mutual capacitance between two objects can be defined by solving for the total charge and using .
Since no actual device holds perfectly equal and opposite charges on each of the two "plates", it is the mutual capacitance that is reported on capacitors.
The collection of coefficients is known as the capacitance matrix, and is the inverse of the elastance matrix.
Capacitors
Main article: CapacitorThe capacitance of the majority of capacitors used in electronic circuits is generally several orders of magnitude smaller than the farad. The most common units of capacitance are the microfarad (μF), nanofarad (nF), picofarad (pF), and, in microcircuits, femtofarad (fF). Some applications also use supercapacitors that can be much larger, as much as hundreds of farads, and parasitic capacitive elements can be less than a femtofarad. Historical texts use other, obsolete submultiples of the farad, such as "mf" and "mfd" for microfarad (μF); "mmf", "mmfd", "pfd", "μμF" for picofarad (pF).
The capacitance can be calculated if the geometry of the conductors and the dielectric properties of the insulator between the conductors are known. Capacitance is proportional to the area of overlap and inversely proportional to the separation between conducting sheets. The closer the sheets are to each other, the greater the capacitance.
An example is the capacitance of a capacitor constructed of two parallel plates both of area separated by a distance . If is sufficiently small with respect to the smallest chord of , there holds, to a high level of accuracy:
where
- is the capacitance, in farads;
- is the area of overlap of the two plates, in square meters;
- is the electric constant ();
- is the relative permittivity (also dielectric constant) of the material in between the plates ( for air); and
- is the separation between the plates, in meters.
The equation is a good approximation if d is small compared to the other dimensions of the plates so that the electric field in the capacitor area is uniform, and the so-called fringing field around the periphery provides only a small contribution to the capacitance.
Combining the equation for capacitance with the above equation for the energy stored in a capacitor, for a flat-plate capacitor the energy stored is: where is the energy, in joules; is the capacitance, in farads; and is the voltage, in volts.
Stray capacitance
Main article: Parasitic capacitanceAny two adjacent conductors can function as a capacitor, though the capacitance is small unless the conductors are close together for long distances or over a large area. This (often unwanted) capacitance is called parasitic or stray capacitance. Stray capacitance can allow signals to leak between otherwise isolated circuits (an effect called crosstalk), and it can be a limiting factor for proper functioning of circuits at high frequency.
Stray capacitance between the input and output in amplifier circuits can be troublesome because it can form a path for feedback, which can cause instability and parasitic oscillation in the amplifier. It is often convenient for analytical purposes to replace this capacitance with a combination of one input-to-ground capacitance and one output-to-ground capacitance; the original configuration – including the input-to-output capacitance – is often referred to as a pi-configuration. Miller's theorem can be used to effect this replacement: it states that, if the gain ratio of two nodes is 1/K, then an impedance of Z connecting the two nodes can be replaced with a Z/1 − K impedance between the first node and ground and a KZ/K − 1 impedance between the second node and ground. Since impedance varies inversely with capacitance, the internode capacitance, C, is replaced by a capacitance of KC from input to ground and a capacitance of (K − 1)C/K from output to ground. When the input-to-output gain is very large, the equivalent input-to-ground impedance is very small while the output-to-ground impedance is essentially equal to the original (input-to-output) impedance.
Capacitance of conductors with simple shapes
Calculating the capacitance of a system amounts to solving the Laplace equation with a constant potential on the 2-dimensional surface of the conductors embedded in 3-space. This is simplified by symmetries. There is no solution in terms of elementary functions in more complicated cases.
For plane situations, analytic functions may be used to map different geometries to each other. See also Schwarz–Christoffel mapping.
| Type | Capacitance | Diagram and definitions |
|---|---|---|
| Parallel-plate capacitor | ||
| Concentric cylinders | 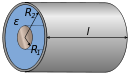
| |
| Eccentric cylinders | 
| |
| Pair of parallel wires | 
| |
| Wire parallel to wall |
| |
| Two parallel coplanar strips |
| |
| Concentric spheres | 
| |
| Two spheres, equal radius |
See also Basic hypergeometric series. | |
| Sphere in front of wall |
| |
| Sphere |
| |
| Circular disc |
| |
| Thin straight wire, finite length |
|
Energy storage
The energy (measured in joules) stored in a capacitor is equal to the work required to push the charges into the capacitor, i.e. to charge it. Consider a capacitor of capacitance C, holding a charge +q on one plate and −q on the other. Moving a small element of charge dq from one plate to the other against the potential difference V = q/C requires the work dW: where W is the work measured in joules, q is the charge measured in coulombs and C is the capacitance, measured in farads.
The energy stored in a capacitor is found by integrating this equation. Starting with an uncharged capacitance (q = 0) and moving charge from one plate to the other until the plates have charge +Q and −Q requires the work W:
Nanoscale systems
The capacitance of nanoscale dielectric capacitors such as quantum dots may differ from conventional formulations of larger capacitors. In particular, the electrostatic potential difference experienced by electrons in conventional capacitors is spatially well-defined and fixed by the shape and size of metallic electrodes in addition to the statistically large number of electrons present in conventional capacitors. In nanoscale capacitors, however, the electrostatic potentials experienced by electrons are determined by the number and locations of all electrons that contribute to the electronic properties of the device. In such devices, the number of electrons may be very small, so the resulting spatial distribution of equipotential surfaces within the device is exceedingly complex.
Single-electron devices
The capacitance of a connected, or "closed", single-electron device is twice the capacitance of an unconnected, or "open", single-electron device. This fact may be traced more fundamentally to the energy stored in the single-electron device whose "direct polarization" interaction energy may be equally divided into the interaction of the electron with the polarized charge on the device itself due to the presence of the electron and the amount of potential energy required to form the polarized charge on the device (the interaction of charges in the device's dielectric material with the potential due to the electron).
Few-electron devices
The derivation of a "quantum capacitance" of a few-electron device involves the thermodynamic chemical potential of an N-particle system given by
whose energy terms may be obtained as solutions of the Schrödinger equation. The definition of capacitance, with the potential difference
may be applied to the device with the addition or removal of individual electrons, and
The "quantum capacitance" of the device is then
This expression of "quantum capacitance" may be written as which differs from the conventional expression described in the introduction where , the stored electrostatic potential energy, by a factor of 1/2 with .
However, within the framework of purely classical electrostatic interactions, the appearance of the factor of 1/2 is the result of integration in the conventional formulation involving the work done when charging a capacitor,
which is appropriate since for systems involving either many electrons or metallic electrodes, but in few-electron systems, . The integral generally becomes a summation. One may trivially combine the expressions of capacitance and electrostatic interaction energy, to obtain
which is similar to the quantum capacitance. A more rigorous derivation is reported in the literature. In particular, to circumvent the mathematical challenges of spatially complex equipotential surfaces within the device, an average electrostatic potential experienced by each electron is utilized in the derivation.
Apparent mathematical differences may be understood more fundamentally. The potential energy, , of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit . As grows large, . Thus, the general expression of capacitance is
In nanoscale devices such as quantum dots, the "capacitor" is often an isolated or partially isolated component within the device. The primary differences between nanoscale capacitors and macroscopic (conventional) capacitors are the number of excess electrons (charge carriers, or electrons, that contribute to the device's electronic behavior) and the shape and size of metallic electrodes. In nanoscale devices, nanowires consisting of metal atoms typically do not exhibit the same conductive properties as their macroscopic, or bulk material, counterparts.
Capacitance in electronic and semiconductor devices
In electronic and semiconductor devices, transient or frequency-dependent current between terminals contains both conduction and displacement components. Conduction current is related to moving charge carriers (electrons, holes, ions, etc.), while displacement current is caused by a time-varying electric field. Carrier transport is affected by electric fields and by a number of physical phenomena - such as carrier drift and diffusion, trapping, injection, contact-related effects, impact ionization, etc. As a result, device admittance is frequency-dependent, and a simple electrostatic formula for capacitance is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is: where is the device admittance, and is the angular frequency.
In general, capacitance is a function of frequency. At high frequencies, capacitance approaches a constant value, equal to "geometric" capacitance, determined by the terminals' geometry and dielectric content in the device. A paper by Steven Laux presents a review of numerical techniques for capacitance calculation. In particular, capacitance can be calculated by a Fourier transform of a transient current in response to a step-like voltage excitation:
Negative capacitance in semiconductor devices
Usually, capacitance in semiconductor devices is positive. However, in some devices and under certain conditions (temperature, applied voltages, frequency, etc.), capacitance can become negative. Non-monotonic behavior of the transient current in response to a step-like excitation has been proposed as the mechanism of negative capacitance. Negative capacitance has been demonstrated and explored in many different types of semiconductor devices.
Measuring capacitance
Main article: Capacitance meterA capacitance meter is a piece of electronic test equipment used to measure capacitance, mainly of discrete capacitors. For most purposes and in most cases the capacitor must be disconnected from circuit.
Many DVMs (digital volt meters) have a capacitance-measuring function. These usually operate by charging and discharging the capacitor under test with a known current and measuring the rate of rise of the resulting voltage; the slower the rate of rise, the larger the capacitance. DVMs can usually measure capacitance from nanofarads to a few hundred microfarads, but wider ranges are not unusual. It is also possible to measure capacitance by passing a known high-frequency alternating current through the device under test and measuring the resulting voltage across it (does not work for polarised capacitors).

More sophisticated instruments use other techniques such as inserting the capacitor-under-test into a bridge circuit. By varying the values of the other legs in the bridge (so as to bring the bridge into balance), the value of the unknown capacitor is determined. This method of indirect use of measuring capacitance ensures greater precision. Through the use of Kelvin connections and other careful design techniques, these instruments can usually measure capacitors over a range from picofarads to farads.
See also
- Capacitive displacement sensor
- Capacity of a set
- Displacement current
- Gauss law
- LCR meter
- Magnetocapacitance
- Quantum capacitance
References
- Harrington, Roger F. (2003). Introduction to Electromagnetic Engineering (1st ed.). Dover Publications. p. 43. ISBN 0-486-43241-6.
- ^ "Lecture notes: Capacitance and Dieletrics" (PDF). University of New South Wales. Archived from the original (PDF) on 26 February 2009.
- "Definition of 'farad'". Collins.
- William D. Greason (1992). Electrostatic discharge in electronics. Research Studies Press. p. 48. ISBN 978-0-86380-136-5.
- Tipler, Paul; Mosca, Gene (2004). Physics for Scientists and Engineers (5th ed.). Macmillan. p. 752. ISBN 978-0-7167-0810-0.
- Massarini, A.; Kazimierczuk, M. K. (1997). "Self capacitance of inductors". IEEE Transactions on Power Electronics. 12 (4): 671–676. Bibcode:1997ITPE...12..671M. CiteSeerX 10.1.1.205.7356. doi:10.1109/63.602562: example of the use of the term 'self capacitance'.
{{cite journal}}: CS1 maint: postscript (link) - Jackson, John David (1999). Classical Electrodynamic (3rd ed.). John Wiley & Sons. p. 43. ISBN 978-0-471-30932-1.
- Maxwell, James (1873). "3". A treatise on electricity and magnetism. Vol. 1. Clarendon Press. p. 88ff.
- "Capacitance: Charge as a Function of Voltage". Av8n.com. Retrieved 20 September 2010.
- Smolić, Ivica; Klajn, Bruno (2021). "Capacitance matrix revisited". Progress in Electromagnetics Research B. 92: 1–18. arXiv:2007.10251. doi:10.2528/PIERB21011501. Retrieved 4 May 2021.
- "Capacitor MF-MMFD Conversion Chart". Just Radios.
- Fundamentals of Electronics. Vol. 1b – Basic Electricity – Alternating Current. Bureau of Naval Personnel. 1965. p. 197.
- Dawes, Chester L. (1973). "Capacitance and potential gradients of eccentric cylindrical condensers". Physics. 4 (2): 81–85. doi:10.1063/1.1745162.
- ^ Jackson, J. D. (1975). Classical Electrodynamics. Wiley. p. 80.
- Binns; Lawrenson (1973). Analysis and computation of electric and magnetic field problems. Pergamon Press. ISBN 978-0-08-016638-4.
- ^ Maxwell, J.;C. (1873). A Treatise on Electricity and Magnetism. Dover. p. 266 ff. ISBN 978-0-486-60637-8.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Rawlins, A.D. (1985). "Note on the capacitance of two closely separated spheres". IMA Journal of Applied Mathematics. 34 (1): 119–120. doi:10.1093/imamat/34.1.119.
- Gasper; Rahman (2004). Basic Hypergeometric Series. Cambridge University Press. p.20-22. ISBN 978-0-521-83357-8.
- Jackson, J.D. (1975). Classical Electrodynamics. Wiley. p. 128, problem 3.3.
- Maxwell, J. C. (1878). "On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness". Proceedings of the London Mathematical Society. IX: 94–101. doi:10.1112/plms/s1-9.1.94.
- Vainshtein, L. A. (1962). "Static boundary problems for a hollow cylinder of finite length. III Approximate formulas". Zhurnal Tekhnicheskoi Fiziki. 32: 1165–1173.
- Jackson, J. D. (2000). "Charge density on thin straight wire, revisited". American Journal of Physics. 68 (9): 789–799. Bibcode:2000AmJPh..68..789J. doi:10.1119/1.1302908.
- Raphael Tsu (2011). Superlattice to Nanoelectronics. Elsevier. pp. 312–315. ISBN 978-0-08-096813-1.
- ^ T. LaFave Jr. (2011). "Discrete charge dielectric model of electrostatic energy". J. Electrostatics. 69 (6): 414–418. arXiv:1203.3798. doi:10.1016/j.elstat.2011.06.006. S2CID 94822190.
- G. J. Iafrate; K. Hess; J. B. Krieger; M. Macucci (1995). "Capacitive nature of atomic-sized structures". Phys. Rev. B. 52 (15): 10737–10739. Bibcode:1995PhRvB..5210737I. doi:10.1103/physrevb.52.10737. PMID 9980157.
- T. LaFave Jr; R. Tsu (March–April 2008). "Capacitance: A property of nanoscale materials based on spatial symmetry of discrete electrons" (PDF). Microelectronics Journal. 39 (3–4): 617–623. doi:10.1016/j.mejo.2007.07.105. Archived from the original (PDF) on 22 February 2014. Retrieved 12 February 2014.
- ^ Laux, S.E. (October 1985). "Techniques for small-signal analysis of semiconductor devices". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 4 (4): 472–481. doi:10.1109/TCAD.1985.1270145. S2CID 13058472.
- Jonscher, A.K. (1986). "The physical origin of negative capacitance". J. Chem. Soc. Faraday Trans. II. 82: 75–81. doi:10.1039/F29868200075.
- Ershov, M.; Liu, H.C.; Li, L.; Buchanan, M.; Wasilewski, Z.R.; Jonscher, A.K. (October 1998). "Negative capacitance effect in semiconductor devices". IEEE Trans. Electron Devices. 45 (10): 2196–2206. arXiv:cond-mat/9806145. Bibcode:1998ITED...45.2196E. doi:10.1109/16.725254. S2CID 204925581.
Further reading
- Tipler, Paul (1998). Physics for Scientists and Engineers: Vol. 2: Electricity and Magnetism, Light (4th ed.). W. H. Freeman. ISBN 1-57259-492-6
- Serway, Raymond; Jewett, John (2003). Physics for Scientists and Engineers (6th ed.). Brooks Cole. ISBN 0-534-40842-7
- Saslow, Wayne M.(2002). Electricity, Magnetism, and Light. Thomson Learning. ISBN 0-12-619455-6. See Chapter 8, and especially pp. 255–259 for coefficients of potential.
External links
- [REDACTED] Media related to Capacitance at Wikimedia Commons


 where
where
 is the charge held,
is the charge held, is the electric potential,
is the electric potential, is the surface charge density,
is the surface charge density, is an infinitesimal element of area on the surface of the conductor, over which the surface charge density is integrated,
is an infinitesimal element of area on the surface of the conductor, over which the surface charge density is integrated, is the length from
is the length from  is the
is the  in free space (i.e. far away from any other charge distributions) is:
in free space (i.e. far away from any other charge distributions) is:

 and
and  , and
, and  gives the
gives the  is given by
is given by  where
where  is the instantaneous rate of change of voltage, and
is the instantaneous rate of change of voltage, and  is the instantaneous rate of change of the capacitance. For most applications, the change in capacitance over time is negligible, so the formula reduces to:
is the instantaneous rate of change of the capacitance. For most applications, the change in capacitance over time is negligible, so the formula reduces to:

 :
:

 does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case,
does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case,  , then the voltage at conductor 1 is given by
, then the voltage at conductor 1 is given by
 and similarly for the other voltages.
and similarly for the other voltages.  , etc. Thus the system can be described by a collection of coefficients known as the elastance matrix or reciprocal capacitance matrix, which is defined as:
, etc. Thus the system can be described by a collection of coefficients known as the elastance matrix or reciprocal capacitance matrix, which is defined as:

 between two objects can be defined by solving for the total charge
between two objects can be defined by solving for the total charge  and using
and using  .
.

 is known as the capacitance matrix, and is the
is known as the capacitance matrix, and is the  separated by a distance
separated by a distance  . If
. If 

 is the
is the  );
); is the
is the  for air); and
for air); and where
where  with a constant potential
with a constant potential  on the 2-dimensional surface of the conductors embedded in 3-space. This is simplified by symmetries. There is no solution in terms of elementary functions in more complicated cases.
on the 2-dimensional surface of the conductors embedded in 3-space. This is simplified by symmetries. There is no solution in terms of elementary functions in more complicated cases.

 :
: 

 : Outer radius
: Outer radius : Inner radius
: Inner radius : Wire length
: Wire length

 : Wire radius
: Wire radius

 : Strip width
: Strip width


 :
: 



 :
: 
 : the q-digamma function
: the q-digamma function : the
: the 
 : Radius
: Radius : Distance,
: Distance, 


 : Radius
: Radius

 : Length
: Length
 where W is the work measured in joules, q is the charge measured in coulombs and C is the capacitance, measured in farads.
where W is the work measured in joules, q is the charge measured in coulombs and C is the capacitance, measured in farads.


 with the potential difference
with the potential difference

 and
and 

 which differs from the conventional expression described in the introduction where
which differs from the conventional expression described in the introduction where  , the stored electrostatic potential energy,
, the stored electrostatic potential energy,
 by a factor of 1/2 with
by a factor of 1/2 with  .
.

 for systems involving either many electrons or metallic electrodes, but in few-electron systems,
for systems involving either many electrons or metallic electrodes, but in few-electron systems,  . The integral generally becomes a summation. One may trivially combine the expressions of capacitance
. The integral generally becomes a summation. One may trivially combine the expressions of capacitance
 and electrostatic interaction energy,
and electrostatic interaction energy,
 to obtain
to obtain

 , of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit
, of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit  . As
. As  grows large,
grows large,  . Thus, the general expression of capacitance is
. Thus, the general expression of capacitance is

 is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is:
is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is:
 where
where  is the device admittance, and
is the device admittance, and  is the angular frequency.
is the angular frequency.
