| Revision as of 02:18, 11 February 2005 editUser2004 (talk | contribs)23,415 edits Poe didn't "discover" explanation← Previous edit | Latest revision as of 18:56, 19 October 2024 edit undoGossamers (talk | contribs)Extended confirmed users4,963 editsmNo edit summary | ||
| (959 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description|Argument in astrophysics against the theory of an unchanging universe}} | |||
| '''Olbers' paradox''', described by the ] ] ] in ] and earlier by ] in ] and ] and ] in the ], is the ]ical statement that in a static ] ] the night sky should be bright. This is sometimes also known as the "dark night sky paradox". | |||
| {{use dmy dates |date=January 2023}} | |||
| ==Assumptions== | |||
| {{distinguish|Oberth paradox}} | |||
| If the universe is assumed to be infinite, containing an infinite number of uniformly distributed luminous ]s, then every line of sight should terminate eventually on the surface of a star. The brightness of a surface is independent of its distance, so every point in the sky should be as bright as the surface of a star. | |||
| ] | |||
| It should be noted that for stars to appear "uniformly distributed" in space they must also be uniformly distributed in time, because the further away one looks, the older what one sees is. On an infinite scale, this means the universe must be infinitely old with no dramatic changes in the nature of stars in that time. | |||
| '''Olbers's<!-- Do not remove an extra "s" - see ] --> paradox''', also known as the '''dark night paradox''' or '''Olbers and Cheseaux's paradox''', is an argument in ] and ] that says the ] of the ] conflicts with the assumption of an infinite and eternal ]. In the hypothetical case that the universe is static, ] at a large scale, and populated by an infinite number of ]s, any line of sight from ] must end at the surface of a star and hence the night sky should be completely illuminated and very bright. This contradicts the observed darkness and non-uniformity of the night sky.<ref name="NYT-20150803">{{cite news |last=Overbye |first=Dennis |author-link=Dennis Overbye |title=The Flip Side of Optimism About Life on Other Planets |url=https://www.nytimes.com/2015/08/04/science/space/the-flip-side-of-optimism-about-life-on-other-planets.html |date=August 3, 2015 |work=] |access-date=October 29, 2015 }}</ref> | |||
| Kepler saw this as an argument for a finite universe, or at least for a finite number of stars, but the argument is not convincing as will be shown below. | |||
| The darkness of the night sky is one piece of evidence for a dynamic universe, such as the ]. That model explains the observed non-uniformity of brightness by invoking ], which increases the ] of ] originating from the Big Bang to ] scale via a process known as ]. The resulting ] has wavelengths much longer (millimeters instead of nanometers), which appear dark to the naked eye and bright for a radio receiver. | |||
| ==Explanations== | |||
| Other explanations for the paradox have been offered, but none have wide acceptance in cosmology. Although he was not the first to describe it, the paradox is popularly named after the German astronomer ] (1758–1840). | |||
| One explanation attempt is that the ] is not transparent, and the light from distant stars is blocked by intermediate dark stars or absorbed by dust or gas, so that there is a bound on the distance from which light can reach the observer. However, this reasoning does not resolve the paradox. According to the ], energy must be conserved, so the intermediate matter would heat up and soon reradiate the energy (possibly at different wavelengths). This would again result in uniform radiation from all directions, which is not observed. | |||
| == History == | |||
| The explanation of the paradox to gain the most scientific consenus points to the finite speed at which light travels through space. Given its finite speed, the light from the most distant star cannot have travelled a further distance, measured in ], than the star itself is old. This explanation was first offered by poet and writer ], who observed: | |||
| :"Were the succession of stars endless, then the background of the sky would present us an uniform luminosity, like that displayed by the Galaxy -–since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all." | |||
| Holding the universe to be approximately 15 billion years old, the furthest expanse that light could have possibly travelled since its creation is an equal number of light years. Thus, even if every infinite trajectory into space from the earth eventually passes through a star in the furthest regions of the universe, the light of all such stars beyond the maximum distance in which light has travelled since the origin of the universe will remain beyond visibility from earth. | |||
| The first one to address the problem of an infinite number of stars and the resulting heat in the Cosmos was ], a 6th-century Greek monk from ], who states in his '']'': "The crystal-made sky sustains the heat of the Sun, the moon, and the infinite number of stars; otherwise, it would have been full of fire, and it could melt or set on fire."<ref>"Cosmas Indicopleustès. Topographie chrétienne, 3 vols.", Ed. Wolska–Conus, W.Paris: Cerf, 1:1968; 2:1970; 3:1973; Sources chrétiennes, Book 10, section 27, line 7 "Cosmas Indicopleustès. Topographia Christiana (4061: 002) Topographie chrétienne, 3 vols.", Ed. Wolska–Conus, W. Paris: Cerf, 1:1968; 2:1970; 3:1973; Sources chrétiennes 141, 159, 197. Book 10, section 27, line 7 ({{lang|grc|Κρυσταλλώδης ἦν ὁ οὐρανὸς ἀπὸ ὑδάτων παγείς· ἐπειδὴ δὲ ἔμελλε δέχεσθαι ἡλίου φλόγα καὶ σελήνης καὶ ἄστρων ἄπειρα πλήθη, καὶ ἦν ὅλος πυρὸς πεπληρωμένος, ἵνα μὴ οὕτως ὑπὸ τῆς θερμότητος λυθῇ ἢ φλεχθῇ ἄστρων ἄπειρα πλήθη, καὶ ἦν ὅλος πυρὸς πεπληρωμένος, ἵνα μὴ οὕτως ὑπὸ τῆς θερμότητος λυθῇ ἢ φλεχθῇ.}})</ref> | |||
| ==Resolutions== | |||
| ]'s ''Darkness at Night: A Riddle of the Universe'' (1987) gives an account of the dark night sky paradox, seen as a problem in the history of science. According to Harrison, the first to conceive of anything like the paradox was ], who was also the first to expound the ] in English and also postulated an infinite universe with infinitely many stars.<ref>{{cite book|title=The Scientific Revolution: The Essential Readings|volume=7|series=Blackwell Essential Readings in History|editor-first=Marcus|editor-last=Hellyer|publisher=]|date=2008|isbn=9780470754771|page=63|url=https://books.google.com/books?id=1VhC63yV-WgC&pg=PA63|quotation=The Puritan Thomas Digges (1546–1595?) was the earliest Englishman to offer a defense of the Copernican theory. ... Accompanying Digges's account is a diagram of the universe portraying the heliocentric system surrounded by the orb of fixed stars, described by Digges as infinitely extended in all dimensions.}}</ref> ] also posed the problem in 1610, and the paradox took its mature form in the 18th-century work of ] and ].<ref name="new cosmos">{{cite book|title=The New Cosmos: An Introduction to Astronomy and Astrophysics|series=Physics and astronomy online|first1=Albrecht|last1=Unsöld|first2=Bodo|last2=Baschek|publisher=Springer|date=2001|isbn=9783540678779|page=485|url=https://books.google.com/books?id=nNnmR8ljctoC&pg=PA485|quotation=The simple observation that the night sky is dark allows far-reaching conclusions to be drawn about the large-scale structure of the universe. This was already realized by J. Kepler (1610), E. Halley (1720), J.-P. Loy de Chesaux (1744), and H. W. M. Olbers (1826).|bibcode=2001ncia.book.....U}}</ref> The paradox is commonly attributed to the ] amateur ] ], who described it in 1823, but Harrison shows convincingly that Olbers was far from the first to pose the problem, nor was his thinking about it particularly valuable. Harrison argues that the first to set out a satisfactory resolution of the paradox was ], in a little known 1901 paper,<ref>For a key extract from this paper, see Harrison (1987), pp. 227–28.</ref> and that ]'s essay '']'' (1848) curiously anticipated some qualitative aspects of Kelvin's argument:<ref name="NYT-20150803" /> | |||
| The paradox is resolvable in a variety of ways. | |||
| {{Blockquote|Were the succession of stars endless, then the background of the sky would present us a uniform luminosity, like that displayed by the Galaxy – since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all.<ref name="eureka">{{cite news|title=Eureka: A Prose Poem|author=Poe, Edgar Allan|date=1848|url=http://books.eserver.org/poetry/poe/eureka.html|url-status=dead|archive-url=https://web.archive.org/web/20080426162441/http://books.eserver.org/poetry/poe/eureka.html|archive-date=2008-04-26}}</ref>}} | |||
| ==The paradox== | |||
| If the universe has existed for only a finite amount of time, as the prevalent ] theory holds, then only the light of finitely many stars has had a chance to reach us yet, and the paradox breaks down. Alternatively, if the universe is expanding and distant stars are receding from us (also a claim of the Big Bang theory), then their light is ] which diminishes their brightness, again resolving the paradox. Either effect alone would resolve the paradox, but according to the Big Bang theory, both are working together; the finiteness of time is the more important effect. Some see the darkness of the night sky to be evidence in support of the ]. | |||
| The paradox is that a static, infinitely old universe with an infinite number of stars distributed in an infinitely large space would be bright rather than dark.<ref name="NYT-20150803" /> | |||
| ] | |||
| Even without the Big Bang theory and its redshift evidence, we may establish the finite age of the universe (in its present form) by a mathematical evaluation of ]. Assume that the amount of mass in stars divided by the total amount of mass in the universe is nonzero. After some length of time, any given star will convert too much hydrogen into helium (or heavier elements) to continue ]. From this we conclude that in unit time, the amount of hydrogen converted into helium by a given star divided by the star's mass is nonzero. Combining this with the earlier statement, we conclude that the amount of hydrogen converted into helium by stars as a whole divided by the mass of the universe is nonzero. There is no known process that can return heavier elements to hydrogen in the necessary quantities, and any would probably violate the second law of ]. Therefore, the amount of time needed for stars to convert ''all'' of the hydrogen in the universe into helium is finite, and it will never change back. After this, only heavier-element-burning stars will exist (and these will die when they hit ], an event known as the ]). This hasn't happened yet, so either the universe is of finite age, it has undergone major changes in its history, or there exists some highly exotic process (for which no direct evidence exists) that produces hydrogen to keep it going. | |||
| To show this, we divide the universe into a series of concentric shells, 1 light year thick. A certain number of stars will be in the shell, say, 1,000,000,000 to 1,000,000,001 light years away. If the universe is homogeneous at a large scale, then there would be four times as many stars in a second shell between 2,000,000,000 and 2,000,000,001 light years away. However, the second shell is twice as far away, so each star in it would appear one quarter as bright as the stars in the first shell. Thus the total light received from the second shell is the same as the total light received from the first shell. | |||
| Thus each shell of a given thickness will produce the same net amount of light regardless of how far away it is. That is, the light of each shell adds to the total amount. Thus the more shells, the more light; and with infinitely many shells, there would be a bright night sky. | |||
| A different resolution, which does not rely on the Big Bang theory, was offered by ]. It holds that the stars in the universe may not be uniformly distributed, but rather ]ly like a ], thus accounting for large dark areas. It is currently not known whether this is true or not, although recent satellite studies have found the ] is isotropic to 1 part in 10000. | |||
| While dark clouds could obstruct the light, these clouds would heat up, until they were as hot as the stars, and then radiate the same amount of light. | |||
| Kepler saw this as an argument for a finite ], or at least for a finite number of stars. In ], it is still possible for the paradox to hold in a finite universe:<ref>{{cite book |last=D'Inverno |first=Ray |title=Introducing Einstein's Relativity |publisher=Oxford University Press |year=1992 |url=https://profmcruz.files.wordpress.com/2018/02/livro-introducing-einsteins-relativity-dinverno.pdf |isbn=9780198596868 }}</ref> Though the sky would not be infinitely bright, every point in the sky would still be like the surface of a star. | |||
| ==Explanation== | |||
| {{See also|Redshift|Lambda-CDM model|expansion of the universe}} | |||
| The poet ] suggested in '']'' that the finite age of the observable universe resolves the apparent paradox.<ref>{{cite web|url=http://xroads.virginia.edu/~hyper/poe/eureka.html |archive-url=https://web.archive.org/web/20001209080900/http://xroads.virginia.edu/~HYPER/poe/eureka.html |url-status=dead |archive-date=9 December 2000 |title=Poe: Eureka |publisher=Xroads.virginia.edu |access-date=2013-05-09}}</ref> More specifically, because the universe is ] (more precisely the ] is only finitely old) and the speed of light is finite, only finitely many stars can be observed from Earth (although the whole universe can be infinite in space).<ref>{{cite web |work=Universe Forum |via=harvard.edu |url=https://lweb.cfa.harvard.edu/seuforum/faq.htm |title=Brief Answers to Cosmic Questions |access-date=27 January 2023 }}</ref><ref>{{cite book |last1=Byrd |first1=Gene |last2=Chernin |first2=Arthur |last3=Teerikorpi |first3=Pekka |last4=Valtonen |first4=Mauri |title=Paths to dark energy: theory and observation |date=2012 |publisher=de Gruyter |location=Berlin |isbn=978-3110258783 |pages=49–50}}</ref> The density of stars within this finite volume is sufficiently low that any line of sight from Earth is unlikely to reach a star. | |||
| However, the ] seems to introduce a new problem: it states that the sky was much brighter in the past, especially at the end of the ] era, when it first became transparent. All points of the local sky at that era were comparable in brightness to the surface of the Sun, due to the high temperature of the universe in that ]; and most light rays will originate not from a star but the relic of the Big Bang. | |||
| This problem is addressed by the fact that the Big Bang theory also involves the ], which can cause the energy of emitted light to be reduced via ]. More specifically, the extremely energetic radiation from the ] has been redshifted to microwave wavelengths (1100 times the length of its original wavelength) as a result of the cosmic expansion, and thus forms the ]. This explains the relatively low light densities and energy levels present in most of our sky today despite the assumed bright nature of the Big Bang. The redshift also affects light from distant ]. | |||
| ==Other factors== | |||
| ===Steady state=== | |||
| The redshift hypothesised in the Big Bang model would by itself explain the darkness of the night sky even if the universe were infinitely old. In the ] the universe is infinitely old and uniform in time as well as space. There is no Big Bang in this model, but there are stars and quasars at arbitrarily great distances. The ] causes the light from these distant stars and quasars to redshift, so that the total light flux from the sky remains finite. Thus the observed radiation density (the sky brightness of ]) can be independent of finiteness of the universe. Mathematically, the total electromagnetic energy density (radiation energy density) in ] from ] is | |||
| <math display="block"> | |||
| u(T) = {U(T)\over V} = \int_0^\infty \frac{8 \pi h \nu^3}{c^3} \frac{1}{e^{\frac{h \nu}{k_B T}} - 1} \, d\nu =\frac{8\pi^5(kT)^4}{15 (hc)^3}, | |||
| </math> | |||
| e.g. for temperature 2.7 K it is 40 fJ/m<sup>3</sup> ... 4.5×10<sup>−31</sup> kg/m<sup>3</sup> and for visible temperature 6000 K we get 1 J/m<sup>3</sup> ... 1.1×10<sup>−17</sup> kg/m<sup>3</sup>. But the total radiation emitted by a star (or other cosmic object) is at most equal to the total ] of ]s in the star. For the density of the ] of about 4.6×10<sup>−28</sup> kg/m<sup>3</sup> and given the known ], the corresponding maximal radiation energy density of 9.2×10<sup>−31</sup> kg/m<sup>3</sup>, i.e. temperature 3.2 K (matching the value observed for the optical radiation temperature by ]<ref>{{cite web|url=http://www.astro.ucla.edu/~wright/Eddington-T0.html| title=Eddington's Temperature of Space|last=Wright|first=Edward L.|date=23 Oct 2006|access-date=10 July 2013}}</ref><ref>{{cite book|url=http://webdev.archive.org/stream/TheInternalConstitutionOfTheStars/Eddington-TheInternalConstitutionOfTheStars#page/n379/mode/2up| title=Eddington's 3.18K "Temperature of Interstellar Space"|pages=371–372|work=The Internal Constitution of the Stars| publisher=]|last=Eddington|first=A.S.|date=1926|access-date=10 July 2013}}</ref>). This is close to the summed energy density of the ] (CMB) and the ]. However, the steady-state model does not predict the angular distribution of the microwave background temperature accurately (as the standard ΛCDM paradigm does).<ref>{{cite web|last1=Wright, E. L.|first1=E. L.|title=Errors in the Steady State and Quasi-SS Models|url=http://www.astro.ucla.edu/~wright/stdystat.htm|publisher=UCLA, Physics and Astronomy Department|access-date=2015-05-28}}</ref> | |||
| ===Brightness=== | |||
| Suppose that the universe were not expanding, and always had the same stellar density; then the temperature of the universe would continually increase as the stars put out more radiation. Eventually, it would reach 3000 K (corresponding to a typical photon energy of 0.3 ] and so a frequency of 7.5×10<sup>13</sup> ]), and the photons would begin to be absorbed by the hydrogen plasma filling most of the universe, rendering outer space opaque. This maximal radiation density corresponds to about {{val|1.2|e=17}} eV/m<sup>3</sup> = {{val|2.1|e=-19|u=kg/m3}}, which is much greater than the observed value of {{val|4.7|e=-31|u=kg/m3}}.<ref name="new cosmos"/> So the sky is about five hundred billion times darker than it would be if the universe was neither expanding nor too young to have reached equilibrium yet. However, recent observations increasing the lower bound on the number of galaxies suggest UV absorption by hydrogen and reemission in near-IR (not visible) wavelengths also plays a role.<ref>{{cite journal |last1=Conselice |first1=Christopher |last2=Wilkinson |first2=Aaron |last3=Duncan |first3=Kenneth |last4=Mortlock |first4=Alice |title=The Evolution of Galaxy Number Density at z < 8 and its Implications |journal=] |date=20 October 2016 |volume=830 |issue=3 |page=83 |doi=10.3847/0004-637X/830/2/83 |arxiv=1607.03909 |bibcode=2016ApJ...830...83C |s2cid=17424588 |doi-access=free }}</ref> | |||
| ===Fractal star distribution=== | |||
| A different resolution, which does not rely on the Big Bang theory, was first proposed by ] in 1908 and later rediscovered by ] in 1974.{{Cn|date=June 2022}} They both postulated that if the stars in the universe were distributed in a hierarchical ] (e.g., similar to ])—the average density of any region diminishes as the region considered increases—it would not be necessary to rely on the Big Bang theory to explain Olbers's paradox. This model would not rule out a Big Bang, but would allow for a dark sky even if the Big Bang had not occurred.{{Cn|date=June 2022}} | |||
| Mathematically, the light received from stars as a function of star distance in a hypothetical fractal cosmos is{{Cn|date=June 2022}} | |||
| <math display="block">\text{light} = \int_{r_0}^\infty L(r) N(r) \,dr,</math> | |||
| where: | |||
| * ''r''<sub>0</sub> = the distance of the nearest star, ''r''<sub>0</sub> > 0; | |||
| * ''r'' = the variable measuring distance from the Earth; | |||
| * ''L''(''r'') = average ] per star at distance ''r''; | |||
| * ''N''(''r'') = number of stars at distance ''r''. | |||
| The function of luminosity from a given distance ''L''(''r'')''N''(''r'') determines whether the light received is finite or infinite. For any luminosity from a given distance {{nowrap|''L''(''r'')''N''(''r'')}} proportional to ''r''<sup>''a''</sup>, <math>\text{light}</math> is infinite for ''a'' ≥ −1 but finite for ''a'' < −1. So if {{nowrap|''L''(''r'')}} is proportional to ''r''<sup>−2</sup>, then for <math>\text{light}</math> to be finite, {{nowrap|''N''(''r'')}} must be proportional to ''r''<sup>''b''</sup>, where ''b'' < 1. For ''b'' = 1, the numbers of stars at a given radius is proportional to that radius. When integrated over the radius, this implies that for ''b'' = 1, the ''total'' number of stars is proportional to ''r''<sup>2</sup>. This would correspond to a ] of 2. Thus the fractal dimension of the universe would need to be less than 2 for this explanation to work. | |||
| This explanation is not widely accepted among cosmologists, since the evidence suggests that the ] of the universe is at least 2.<ref>{{cite journal |author=Joyce, M. |display-authors=4 |author2=Labini, F. S. |author3=Gabrielli, A. |author4=Montouri, M. |author5=Pietronero, L. |date=2005 |title=Basic Properties of Galaxy Clustering in the light of recent results from the Sloan Digital Sky Survey |journal=Astronomy and Astrophysics |volume=443 |issue=11 |arxiv=astro-ph/0501583 |doi= 10.1051/0004-6361:20053658 |pages=11–16 |bibcode=2005A&A...443...11J|s2cid=14466810 }}</ref><ref>{{cite journal |author=Labini, F. S. |author2=Vasilyev, N. L. |author3=Pietronero, L. |author4=Baryshev, Y. |date=2009 |title=Absence of self-averaging and of homogeneity in the large scale galaxy distribution |journal=Europhys. Lett. |volume=86 |issue= 4|page= 49001|arxiv=0805.1132 |doi= 10.1209/0295-5075/86/49001 |bibcode=2009EL.....8649001S|s2cid=15259697 }}</ref><ref>{{cite journal |author=Hogg, David W. |display-authors=4 |author2=Eisenstein, Daniel J. |author3=Blanton, Michael R. |author4=Bahcall, Neta A. |author5=Brinkmann, J. |author6=Gunn, James E. |author7=Schneider, Donald P. |date=2005 |title=Cosmic homogeneity demonstrated with luminous red galaxies |journal=] |volume=624 |issue= 1|pages=54–58 |arxiv=astro-ph/0411197 |doi= 10.1086/429084 |bibcode=2005ApJ...624...54H|s2cid=15957886 }}</ref> Moreover, the majority of cosmologists accept the ],{{Citation needed|date=August 2016}} which assumes that matter at the scale of billions of light years is distributed ]ally. Contrarily, fractal cosmology requires ] matter distribution at the largest scales. | |||
| == See also == | |||
| * ] | |||
| * ] | |||
| * ] | |||
| ==References== | ==References== | ||
| {{Reflist|30em}} | |||
| ==Further reading== | |||
| * | |||
| *{{cite book <!--|authorlink=Edward Robert Harrison--> |first=Edward Robert |last=Harrison |year=1987 |title=Darkness at Night: A Riddle of the Universe |publisher=Harvard University Press |isbn=9780674192713 }} | |||
| * | |||
| *{{cite book <!--|authorlink=Edward Robert Harrison--> |first=Edward Robert |last=Harrison |year=2000 |title=Cosmology: The Science of the Universe |edition=2nd |publisher=Cambridge University Press |chapter=Darkness at night |isbn=9781009215701 }} | |||
| * | |||
| * |
*{{cite journal |last1=Wesson |first1= Paul |date=1991 |title=Olbers' paradox and the spectral intensity of the extragalactic background light |bibcode=1991ApJ...367..399W |journal=] |volume=367 |pages=399–406 |doi=10.1086/169638}} | ||
| *{{cite book |last=Zamarovský |first=Peter |year=2013 |title=Why is it Dark at Night? Story of Dark Night Sky Paradox |publisher=AuthorHouseUK |isbn=978-1491878804 }} | |||
| * Edward Harrison, ''Darkness at Night: A Riddle of the Universe'', Harvard University Press, 1987 | |||
| * Scott, Douglas, and Martin White, "''''". | |||
| ==External links== | |||
| <!--Categories--> | |||
| {{Library resources box}} | |||
| * | |||
| <!--Interwiki--> | |||
| * | |||
| * | |||
| * {{MathPages|id=home/kmath141/kmath141|title=On Olber's Paradox}} | |||
| * physics.org page about Olbers's paradox | |||
| * A 60-second animation from the ] exploring the question with Alice and Bob in Wonderland | |||
| {{Paradoxes}} | |||
| {{Portal bar|Physics|Astronomy|Stars|Spaceflight|Outer space|Solar System}} | |||
| {{Authority control}} | |||
| <!-- ] and ] are too general. --> | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| ] | |||
Latest revision as of 18:56, 19 October 2024
Argument in astrophysics against the theory of an unchanging universeNot to be confused with Oberth paradox.
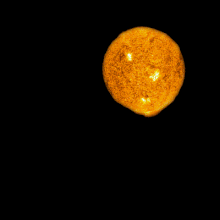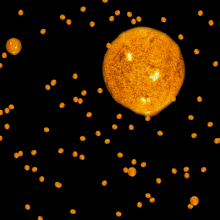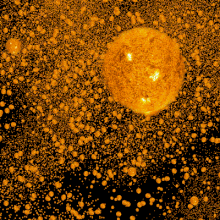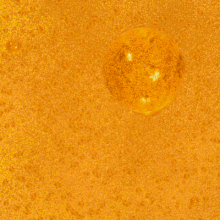
Olbers's paradox, also known as the dark night paradox or Olbers and Cheseaux's paradox, is an argument in astrophysics and physical cosmology that says the darkness of the night sky conflicts with the assumption of an infinite and eternal static universe. In the hypothetical case that the universe is static, homogeneous at a large scale, and populated by an infinite number of stars, any line of sight from Earth must end at the surface of a star and hence the night sky should be completely illuminated and very bright. This contradicts the observed darkness and non-uniformity of the night sky.
The darkness of the night sky is one piece of evidence for a dynamic universe, such as the Big Bang model. That model explains the observed non-uniformity of brightness by invoking expansion of the universe, which increases the wavelength of visible light originating from the Big Bang to microwave scale via a process known as redshift. The resulting microwave radiation background has wavelengths much longer (millimeters instead of nanometers), which appear dark to the naked eye and bright for a radio receiver.
Other explanations for the paradox have been offered, but none have wide acceptance in cosmology. Although he was not the first to describe it, the paradox is popularly named after the German astronomer Heinrich Wilhelm Olbers (1758–1840).
History
The first one to address the problem of an infinite number of stars and the resulting heat in the Cosmos was Cosmas Indicopleustes, a 6th-century Greek monk from Alexandria, who states in his Topographia Christiana: "The crystal-made sky sustains the heat of the Sun, the moon, and the infinite number of stars; otherwise, it would have been full of fire, and it could melt or set on fire."
Edward Robert Harrison's Darkness at Night: A Riddle of the Universe (1987) gives an account of the dark night sky paradox, seen as a problem in the history of science. According to Harrison, the first to conceive of anything like the paradox was Thomas Digges, who was also the first to expound the Copernican system in English and also postulated an infinite universe with infinitely many stars. Kepler also posed the problem in 1610, and the paradox took its mature form in the 18th-century work of Halley and Cheseaux. The paradox is commonly attributed to the German amateur astronomer Heinrich Wilhelm Olbers, who described it in 1823, but Harrison shows convincingly that Olbers was far from the first to pose the problem, nor was his thinking about it particularly valuable. Harrison argues that the first to set out a satisfactory resolution of the paradox was Lord Kelvin, in a little known 1901 paper, and that Edgar Allan Poe's essay Eureka (1848) curiously anticipated some qualitative aspects of Kelvin's argument:
Were the succession of stars endless, then the background of the sky would present us a uniform luminosity, like that displayed by the Galaxy – since there could be absolutely no point, in all that background, at which would not exist a star. The only mode, therefore, in which, under such a state of affairs, we could comprehend the voids which our telescopes find in innumerable directions, would be by supposing the distance of the invisible background so immense that no ray from it has yet been able to reach us at all.
The paradox
The paradox is that a static, infinitely old universe with an infinite number of stars distributed in an infinitely large space would be bright rather than dark.

To show this, we divide the universe into a series of concentric shells, 1 light year thick. A certain number of stars will be in the shell, say, 1,000,000,000 to 1,000,000,001 light years away. If the universe is homogeneous at a large scale, then there would be four times as many stars in a second shell between 2,000,000,000 and 2,000,000,001 light years away. However, the second shell is twice as far away, so each star in it would appear one quarter as bright as the stars in the first shell. Thus the total light received from the second shell is the same as the total light received from the first shell.
Thus each shell of a given thickness will produce the same net amount of light regardless of how far away it is. That is, the light of each shell adds to the total amount. Thus the more shells, the more light; and with infinitely many shells, there would be a bright night sky.
While dark clouds could obstruct the light, these clouds would heat up, until they were as hot as the stars, and then radiate the same amount of light.
Kepler saw this as an argument for a finite observable universe, or at least for a finite number of stars. In general relativity theory, it is still possible for the paradox to hold in a finite universe: Though the sky would not be infinitely bright, every point in the sky would still be like the surface of a star.
Explanation
See also: Redshift, Lambda-CDM model, and expansion of the universeThe poet Edgar Allan Poe suggested in Eureka: A Prose Poem that the finite age of the observable universe resolves the apparent paradox. More specifically, because the universe is finitely old (more precisely the Stelliferous Era is only finitely old) and the speed of light is finite, only finitely many stars can be observed from Earth (although the whole universe can be infinite in space). The density of stars within this finite volume is sufficiently low that any line of sight from Earth is unlikely to reach a star.
However, the Big Bang theory seems to introduce a new problem: it states that the sky was much brighter in the past, especially at the end of the recombination era, when it first became transparent. All points of the local sky at that era were comparable in brightness to the surface of the Sun, due to the high temperature of the universe in that era; and most light rays will originate not from a star but the relic of the Big Bang.
This problem is addressed by the fact that the Big Bang theory also involves the expansion of the universe, which can cause the energy of emitted light to be reduced via redshift. More specifically, the extremely energetic radiation from the Big Bang has been redshifted to microwave wavelengths (1100 times the length of its original wavelength) as a result of the cosmic expansion, and thus forms the cosmic microwave background radiation. This explains the relatively low light densities and energy levels present in most of our sky today despite the assumed bright nature of the Big Bang. The redshift also affects light from distant galaxies.
Other factors
Steady state
The redshift hypothesised in the Big Bang model would by itself explain the darkness of the night sky even if the universe were infinitely old. In the Steady state theory the universe is infinitely old and uniform in time as well as space. There is no Big Bang in this model, but there are stars and quasars at arbitrarily great distances. The expansion of the universe causes the light from these distant stars and quasars to redshift, so that the total light flux from the sky remains finite. Thus the observed radiation density (the sky brightness of extragalactic background light) can be independent of finiteness of the universe. Mathematically, the total electromagnetic energy density (radiation energy density) in thermodynamic equilibrium from Planck's law is
e.g. for temperature 2.7 K it is 40 fJ/m ... 4.5×10 kg/m and for visible temperature 6000 K we get 1 J/m ... 1.1×10 kg/m. But the total radiation emitted by a star (or other cosmic object) is at most equal to the total nuclear binding energy of isotopes in the star. For the density of the observable universe of about 4.6×10 kg/m and given the known abundance of the chemical elements, the corresponding maximal radiation energy density of 9.2×10 kg/m, i.e. temperature 3.2 K (matching the value observed for the optical radiation temperature by Arthur Eddington). This is close to the summed energy density of the cosmic microwave background (CMB) and the cosmic neutrino background. However, the steady-state model does not predict the angular distribution of the microwave background temperature accurately (as the standard ΛCDM paradigm does).
Brightness
Suppose that the universe were not expanding, and always had the same stellar density; then the temperature of the universe would continually increase as the stars put out more radiation. Eventually, it would reach 3000 K (corresponding to a typical photon energy of 0.3 eV and so a frequency of 7.5×10 Hz), and the photons would begin to be absorbed by the hydrogen plasma filling most of the universe, rendering outer space opaque. This maximal radiation density corresponds to about 1.2×10 eV/m = 2.1×10 kg/m, which is much greater than the observed value of 4.7×10 kg/m. So the sky is about five hundred billion times darker than it would be if the universe was neither expanding nor too young to have reached equilibrium yet. However, recent observations increasing the lower bound on the number of galaxies suggest UV absorption by hydrogen and reemission in near-IR (not visible) wavelengths also plays a role.
Fractal star distribution
A different resolution, which does not rely on the Big Bang theory, was first proposed by Carl Charlier in 1908 and later rediscovered by Benoît Mandelbrot in 1974. They both postulated that if the stars in the universe were distributed in a hierarchical fractal cosmology (e.g., similar to Cantor dust)—the average density of any region diminishes as the region considered increases—it would not be necessary to rely on the Big Bang theory to explain Olbers's paradox. This model would not rule out a Big Bang, but would allow for a dark sky even if the Big Bang had not occurred.
Mathematically, the light received from stars as a function of star distance in a hypothetical fractal cosmos is
where:
- r0 = the distance of the nearest star, r0 > 0;
- r = the variable measuring distance from the Earth;
- L(r) = average luminosity per star at distance r;
- N(r) = number of stars at distance r.
The function of luminosity from a given distance L(r)N(r) determines whether the light received is finite or infinite. For any luminosity from a given distance L(r)N(r) proportional to r, is infinite for a ≥ −1 but finite for a < −1. So if L(r) is proportional to r, then for to be finite, N(r) must be proportional to r, where b < 1. For b = 1, the numbers of stars at a given radius is proportional to that radius. When integrated over the radius, this implies that for b = 1, the total number of stars is proportional to r. This would correspond to a fractal dimension of 2. Thus the fractal dimension of the universe would need to be less than 2 for this explanation to work.
This explanation is not widely accepted among cosmologists, since the evidence suggests that the fractal dimension of the universe is at least 2. Moreover, the majority of cosmologists accept the cosmological principle, which assumes that matter at the scale of billions of light years is distributed isotropically. Contrarily, fractal cosmology requires anisotropic matter distribution at the largest scales.
See also
References
- ^ Overbye, Dennis (3 August 2015). "The Flip Side of Optimism About Life on Other Planets". The New York Times. Retrieved 29 October 2015.
- "Cosmas Indicopleustès. Topographie chrétienne, 3 vols.", Ed. Wolska–Conus, W.Paris: Cerf, 1:1968; 2:1970; 3:1973; Sources chrétiennes, Book 10, section 27, line 7 "Cosmas Indicopleustès. Topographia Christiana (4061: 002) Topographie chrétienne, 3 vols.", Ed. Wolska–Conus, W. Paris: Cerf, 1:1968; 2:1970; 3:1973; Sources chrétiennes 141, 159, 197. Book 10, section 27, line 7 (Κρυσταλλώδης ἦν ὁ οὐρανὸς ἀπὸ ὑδάτων παγείς· ἐπειδὴ δὲ ἔμελλε δέχεσθαι ἡλίου φλόγα καὶ σελήνης καὶ ἄστρων ἄπειρα πλήθη, καὶ ἦν ὅλος πυρὸς πεπληρωμένος, ἵνα μὴ οὕτως ὑπὸ τῆς θερμότητος λυθῇ ἢ φλεχθῇ ἄστρων ἄπειρα πλήθη, καὶ ἦν ὅλος πυρὸς πεπληρωμένος, ἵνα μὴ οὕτως ὑπὸ τῆς θερμότητος λυθῇ ἢ φλεχθῇ.)
- Hellyer, Marcus, ed. (2008). The Scientific Revolution: The Essential Readings. Blackwell Essential Readings in History. Vol. 7. John Wiley & Sons. p. 63. ISBN 9780470754771.
The Puritan Thomas Digges (1546–1595?) was the earliest Englishman to offer a defense of the Copernican theory. ... Accompanying Digges's account is a diagram of the universe portraying the heliocentric system surrounded by the orb of fixed stars, described by Digges as infinitely extended in all dimensions.
- ^ Unsöld, Albrecht; Baschek, Bodo (2001). The New Cosmos: An Introduction to Astronomy and Astrophysics. Physics and astronomy online. Springer. p. 485. Bibcode:2001ncia.book.....U. ISBN 9783540678779.
The simple observation that the night sky is dark allows far-reaching conclusions to be drawn about the large-scale structure of the universe. This was already realized by J. Kepler (1610), E. Halley (1720), J.-P. Loy de Chesaux (1744), and H. W. M. Olbers (1826).
- For a key extract from this paper, see Harrison (1987), pp. 227–28.
- Poe, Edgar Allan (1848). "Eureka: A Prose Poem". Archived from the original on 26 April 2008.
- D'Inverno, Ray (1992). Introducing Einstein's Relativity (PDF). Oxford University Press. ISBN 9780198596868.
- "Poe: Eureka". Xroads.virginia.edu. Archived from the original on 9 December 2000. Retrieved 9 May 2013.
- "Brief Answers to Cosmic Questions". Universe Forum. Retrieved 27 January 2023 – via harvard.edu.
- Byrd, Gene; Chernin, Arthur; Teerikorpi, Pekka; Valtonen, Mauri (2012). Paths to dark energy: theory and observation. Berlin: de Gruyter. pp. 49–50. ISBN 978-3110258783.
- Wright, Edward L. (23 October 2006). "Eddington's Temperature of Space". Retrieved 10 July 2013.
- Eddington, A.S. (1926). Eddington's 3.18K "Temperature of Interstellar Space". Cambridge University Press. pp. 371–372. Retrieved 10 July 2013.
{{cite book}}:|work=ignored (help) - Wright, E. L., E. L. "Errors in the Steady State and Quasi-SS Models". UCLA, Physics and Astronomy Department. Retrieved 28 May 2015.
- Conselice, Christopher; Wilkinson, Aaron; Duncan, Kenneth; Mortlock, Alice (20 October 2016). "The Evolution of Galaxy Number Density at z < 8 and its Implications". The Astrophysical Journal. 830 (3): 83. arXiv:1607.03909. Bibcode:2016ApJ...830...83C. doi:10.3847/0004-637X/830/2/83. S2CID 17424588.
- Joyce, M.; Labini, F. S.; Gabrielli, A.; Montouri, M.; et al. (2005). "Basic Properties of Galaxy Clustering in the light of recent results from the Sloan Digital Sky Survey". Astronomy and Astrophysics. 443 (11): 11–16. arXiv:astro-ph/0501583. Bibcode:2005A&A...443...11J. doi:10.1051/0004-6361:20053658. S2CID 14466810.
- Labini, F. S.; Vasilyev, N. L.; Pietronero, L.; Baryshev, Y. (2009). "Absence of self-averaging and of homogeneity in the large scale galaxy distribution". Europhys. Lett. 86 (4): 49001. arXiv:0805.1132. Bibcode:2009EL.....8649001S. doi:10.1209/0295-5075/86/49001. S2CID 15259697.
- Hogg, David W.; Eisenstein, Daniel J.; Blanton, Michael R.; Bahcall, Neta A.; et al. (2005). "Cosmic homogeneity demonstrated with luminous red galaxies". The Astrophysical Journal. 624 (1): 54–58. arXiv:astro-ph/0411197. Bibcode:2005ApJ...624...54H. doi:10.1086/429084. S2CID 15957886.
Further reading
- Harrison, Edward Robert (1987). Darkness at Night: A Riddle of the Universe. Harvard University Press. ISBN 9780674192713.
- Harrison, Edward Robert (2000). "Darkness at night". Cosmology: The Science of the Universe (2nd ed.). Cambridge University Press. ISBN 9781009215701.
- Wesson, Paul (1991). "Olbers' paradox and the spectral intensity of the extragalactic background light". The Astrophysical Journal. 367: 399–406. Bibcode:1991ApJ...367..399W. doi:10.1086/169638.
- Zamarovský, Peter (2013). Why is it Dark at Night? Story of Dark Night Sky Paradox. AuthorHouseUK. ISBN 978-1491878804.
External links
Library resources aboutOlbers's paradox
- Relativity FAQ about Olbers's paradox
- Astronomy FAQ about Olbers's paradox
- Cosmology FAQ about Olbers's paradox
- "On Olber's Paradox". MathPages.com.
- Why is the sky dark? physics.org page about Olbers's paradox
- Why is it dark at night? A 60-second animation from the Perimeter Institute exploring the question with Alice and Bob in Wonderland


 is infinite for a ≥ −1 but finite for a < −1. So if L(r) is proportional to r, then for
is infinite for a ≥ −1 but finite for a < −1. So if L(r) is proportional to r, then for