| Revision as of 21:05, 9 January 2025 editGreatStellatedDodecahedron (talk | contribs)Autopatrolled, Extended confirmed users1,156 edits New article on the law of constancy of interfacial angles | Latest revision as of 00:02, 10 January 2025 edit undoCitation bot (talk | contribs)Bots5,436,028 edits Alter: pages, section, url, title. URLs might have been anonymized. Add: pmid, chapter-url-access, chapter-url. Removed or converted URL. Removed parameters. Formatted dashes. Some additions/deletions were parameter name changes. | Use this bot. Report bugs. | Suggested by Jay8g | #UCB_toolbar | ||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 16: | Line 16: | ||
| ] | ] | ||
| The law of the constancy of interfacial angles was first observed by the Danish physician ] when studying quartz crystals<ref name="Senechal">{{cite book |last1=Senechal |first1=Marjorie |editor1-last=Lima-de-Faria |editor1-first=J. |title=Historical atlas of crystallography |date=1990 |publisher=Published for International Union of Crystallography by Kluwer Academic Publishers |location=Dordrecht ; Boston |isbn=079230649X |page=44 |chapter=Brief history of geometrical crystallography |url=https://archive.org/details/historicalatlaso0000unse_p0f2/page/44/mode/2up |url-access=registration |access-date=24 December 2024}}</ref><ref name="Schuh">{{cite book |last1=Schuh |first1=Curtis P. |title=Mineralogy and Crystallography: An Annotated Biobibliography of Books Published 1469 to 1919 |section=Steno, Nicolaus |url=https://mineralogicalrecord.com/new_biobibliography/steno-nicolaus/ |url-status=live |access-date=8 January 2025 |archive-url=https://archive.org/details/BioBib_Mineralogy_2007_Vol_2/page/n611/mode/2up |archive-date=25 August 2007 |volume=2 |pages= |
The law of the constancy of interfacial angles was first observed by the Danish physician ] when studying quartz crystals<ref name="Senechal">{{cite book |last1=Senechal |first1=Marjorie |editor1-last=Lima-de-Faria |editor1-first=J. |title=Historical atlas of crystallography |date=1990 |publisher=Published for International Union of Crystallography by Kluwer Academic Publishers |location=Dordrecht ; Boston |isbn=079230649X |page=44 |chapter=Brief history of geometrical crystallography |chapter-url=https://archive.org/details/historicalatlaso0000unse_p0f2/page/44/mode/2up |chapter-url-access=registration |access-date=24 December 2024}}</ref><ref name="Schuh">{{cite book |last1=Schuh |first1=Curtis P. |title=Mineralogy and Crystallography: An Annotated Biobibliography of Books Published 1469 to 1919 |section=Steno, Nicolaus |url=https://mineralogicalrecord.com/new_biobibliography/steno-nicolaus/ |url-status=live |access-date=8 January 2025 |archive-url=https://archive.org/details/BioBib_Mineralogy_2007_Vol_2/page/n611/mode/2up |archive-date=25 August 2007 |volume=2 |pages=1381–1382}}</ref> (''De solido intra solidum naturaliter contento'', Florence, 1669),<ref name="Steno1">{{cite book |last1=Steno |first1= Nicolas |year=1669 |url=https://archive.org/details/nicolaistenonisd00sten |language=Latin |access-date=8 January 2025 |title=De solido intra solidum naturaliter contento |publisher=Star |location=Florence}}</ref><ref name="Steno2">{{cite book |last1=Steno |first1=Nicolaus |title=The prodromus of Nicolaus Steno's dissertation concerning a solid body enclosed by process of nature within a solid |year=1916 |orig-year=1669 |translator-last1=Winter |translator-first1=John Garrett |publisher=The Macmillan Company |location=New York, London |page=272 |url=https://archive.org/details/prodromusnicola00stengoog/page/n128/mode/2up |access-date=9 January 2025 |language=English |quote=Figures 5 and 6 belong to the class of those which I could present in countless numbers to prove that in the plane of the axis both the number and the length of the sides are changed in various ways without changing the angles.}}</ref> who noted that, although the crystals differed in appearance from one to another, the angles between corresponding faces were always the same.<ref name="Ladd">{{cite book |last1=Ladd |first1=Marcus Frederick Charles |title=Symmetry of crystals and molecules |date=2014 |publisher=Oxford University Press |location=Oxford |isbn=9780199670888 |pages=13–15}}</ref> | ||
| The law was also observed by ] (''Riflessioni filosofiche dedotte dalle figure de Sali'', Bologna, 1688), but it was generalized and firmly established by ] (''Cristallographie'', Paris, 1783)<ref name="Romé de L'Isle">{{cite book |last1=Romé de L'Isle |first1=Jean Baptiste Louis de |title=Cristallographie |date=1783 |publisher=De l'imprimerie de Monsieur |location=Paris |chapter=Préface |url=https://archive.org/details/cristallographi01unkngoog/page/n4/mode/2up |language=French |access-date=8 January 2025}}</ref> who accurately measured the interfacial angles of a great variety of crystals, using the ] designed by ] and noted that the angles are characteristic of a substance.<ref>{{cite book |last1=Metzger |first1=Hélène |title=La Gènese de la Science de Cristaux |year=1969 |orig-year=1918 |publisher=Albert Blanchard |location=Paris |pages= |
The law was also observed by ] (''Riflessioni filosofiche dedotte dalle figure de Sali'', Bologna, 1688), but it was generalized and firmly established by ] (''Cristallographie'', Paris, 1783)<ref name="Romé de L'Isle">{{cite book |last1=Romé de L'Isle |first1=Jean Baptiste Louis de |title=Cristallographie |date=1783 |publisher=De l'imprimerie de Monsieur |location=Paris |chapter=Préface |url=https://archive.org/details/cristallographi01unkngoog/page/n4/mode/2up |language=French |access-date=8 January 2025}}</ref> who accurately measured the interfacial angles of a great variety of crystals, using the ] designed by ] and noted that the angles are characteristic of a substance.<ref>{{cite book |last1=Metzger |first1=Hélène |title=La Gènese de la Science de Cristaux |year=1969 |orig-year=1918 |publisher=Albert Blanchard |location=Paris |pages=67–68 |url=https://gallica.bnf.fr/ark:/12148/bpt6k260731/f66.item |url-status=live |archive-url=https://archive.org/details/metzger-helene-la-genese-de-la-science/page/67/mode/2up |archive-date=2 October 2021 |language=French |access-date=8 January 2025}}</ref><ref name="Phillips">{{cite book |last1=Phillips |first1=F. C. |title=An Introduction To Crystallography |date=1963 |publisher=John Wiley & Sons |location=New York |pages=12–14 |edition=3rd |url=https://archive.org/details/introductiontocr0000fcph/page/12/mode/2up |url-access=registration |access-date=8 January 2025}}</ref> Carangeot was a student of Romé de L’Isle at the time of his invention of the basic crystallographic measuring instrument.<ref name="Burke">{{cite book |last1=Burke |first1=John G. |title=Origins of the science of crystals |publisher=University of California Press |location=Berkley and Los Angeles |year=1966 |pages=69–70 |url=https://archive.org/details/originsofscience0000burk/page/68/mode/2up |url-access=registration |access-date=8 January 2025}}</ref><ref name="Scholz">{{cite book |last1=Scholz |first1=Erhard |title=Symmetrie, Gruppe, Dualität |date=1989 |publisher=Birkhäuser |location=Basel Boston Berlin |isbn=3764319747 |language=German |pages=19, 21}}</ref><ref name="Authier">{{cite book |last1=Authier |first1=André |title=Early days of X-ray crystallography |date=2015 |publisher=Oxford University Press |location=Oxford |isbn=9780198754053 |doi=10.1093/acprof:oso/9780199659845.003.0011 |section= 11.11 J.-B. L. Romé de l'Isle and the law of the constancy of interfacial angles, 1783 |pages=313–317 |url=https://academic.oup.com/book/8011/chapter/153379723 |url-access=registration |access-date=8 January 2025}}</ref> | ||
| A French crystallographer, ], showed in 1774<ref name="Haüy1">{{cite book |last1=Haüy |first1=René-Just |title=Essai d'une théorie sur la structure des crystaux, appliquée à plusieurs genres de substances crystallisées |date=1784 |publisher=Gogué et Née de La Rochelle |location=Paris |url=https://gallica.bnf.fr/ark:/12148/bpt6k1060890.r=.langFR |url-status=live |access-date=8 January 2025 |archive-url=https://archive.org/details/b28762411_0001/page/n5/mode/2up |archive-date=26 September 2016 |language=French}}</ref> that the known interfacial angles could be accounted for if the crystal were made up of minute building blocks (''molécules intégrantes'')<ref name="Britannica">{{cite web |title= |
A French crystallographer, ], showed in 1774<ref name="Haüy1">{{cite book |last1=Haüy |first1=René-Just |title=Essai d'une théorie sur la structure des crystaux, appliquée à plusieurs genres de substances crystallisées |date=1784 |publisher=Gogué et Née de La Rochelle |location=Paris |url=https://gallica.bnf.fr/ark:/12148/bpt6k1060890.r=.langFR |url-status=live |access-date=8 January 2025 |archive-url=https://archive.org/details/b28762411_0001/page/n5/mode/2up |archive-date=26 September 2016 |language=French}}</ref> that the known interfacial angles could be accounted for if the crystal were made up of minute building blocks (''molécules intégrantes'')<ref name="Britannica">{{cite web |title=Steno's law |url=https://www.britannica.com/science/Stenos-law |publisher=Encyclopaedia Britannica |access-date=7 January 2025}}</ref> that correspond approximately to the present-day ]s. | ||
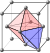
| In the diagram, the green dodecahedron on the left is built from cubical units, with the faces having a ] of (210). Unlike the ] on the right, its faces are not regular pentagons, but they are close to regular in appearance. The piling of the cubical units forms the pentagonal dodecahedron of ] ]. The decrement of the layers is in the proportion of 2:1, which leads to a dihedral angle at the top edge '''pq''' of 126° 87′, closely corresponding to that of the empirical crystal, of 127° 56′. The diagram is based on an 1801 drawing by ].<ref name="Haüy2">{{cite book |last1=Haüy |first1=René Just |title=Traité de minéralogie |date=1801 |publisher=Chez Louis |location=Paris |volume=Caractère Minéralogique |page=II, fig. 16 |url=https://gallica.bnf.fr/ark:/12148/bpt6k9760845h/f11.item |access-date=8 January 2025 |language=French}}</ref><ref name="Haüy3">{{cite book |last1=Haüy |first1=René Just |title=Traité de cristallographie |date=1822 |publisher=Bachelier |location=Paris |volume=Atlas |page=8, fig. 75 |url=https://archive.org/details/traitdecristal00ha/page/8/mode/2up |url-access=registration |access-date=7 January 2025 |language=French}}</ref> | In the diagram, the green dodecahedron on the left is built from cubical units, with the faces having a ] of (210). Unlike the ] on the right, its faces are not regular pentagons, but they are close to regular in appearance. The piling of the cubical units forms the pentagonal dodecahedron of ] ]. The decrement of the layers is in the proportion of 2:1, which leads to a dihedral angle at the top edge '''pq''' of 126° 87′, closely corresponding to that of the empirical crystal, of 127° 56′. The diagram is based on an 1801 drawing by ].<ref name="Haüy2">{{cite book |last1=Haüy |first1=René Just |title=Traité de minéralogie |date=1801 |publisher=Chez Louis |location=Paris |volume=Caractère Minéralogique |page=II, fig. 16 |url=https://gallica.bnf.fr/ark:/12148/bpt6k9760845h/f11.item |access-date=8 January 2025 |language=French}}</ref><ref name="Haüy3">{{cite book |last1=Haüy |first1=René Just |title=Traité de cristallographie |date=1822 |publisher=Bachelier |location=Paris |volume=Atlas |page=8, fig. 75 |url=https://archive.org/details/traitdecristal00ha/page/8/mode/2up |url-access=registration |access-date=7 January 2025 |language=French}}</ref> | ||
| Line 31: | Line 31: | ||
| The angles between the various faces of a crystal remain unchanged throughout its growth. Crystals ] by addition of material to existing faces, this material being deposited parallel to the already existing surfaces. Consequently, if more material is added to one face than to another, the faces become unalike in size and shape, nevertheless the interfacial angles between them remain the same.<ref name="Sunagawa">{{cite book |last1=Sunagawa |first1=Ichirō |title=Crystals: growth, morphology, and perfection |date=2007 |publisher=Cambridge University Press |location=Cambridge |isbn=9780521841894}}</ref> | The angles between the various faces of a crystal remain unchanged throughout its growth. Crystals ] by addition of material to existing faces, this material being deposited parallel to the already existing surfaces. Consequently, if more material is added to one face than to another, the faces become unalike in size and shape, nevertheless the interfacial angles between them remain the same.<ref name="Sunagawa">{{cite book |last1=Sunagawa |first1=Ichirō |title=Crystals: growth, morphology, and perfection |date=2007 |publisher=Cambridge University Press |location=Cambridge |isbn=9780521841894}}</ref> | ||
| Crystals generally exhibit ], that is their properties are dependent on their direction. In particular, crystals cleave in specific directions, namely those parallel to the planes of the lattice structure.<ref name="Hoffmann">{{cite book |last1=Hoffmann |first1=Frank |title=Introduction to crystallography |date=2020 |publisher=Springer |location=Cham, Switzerland |isbn=9783030351090 |pages= |
Crystals generally exhibit ], that is their properties are dependent on their direction. In particular, crystals cleave in specific directions, namely those parallel to the planes of the lattice structure.<ref name="Hoffmann">{{cite book |last1=Hoffmann |first1=Frank |title=Introduction to crystallography |date=2020 |publisher=Springer |location=Cham, Switzerland |isbn=9783030351090 |pages=238–239 |edition=1st |doi=10.1007/978-3-030-35110-6}}</ref> ] preferentially occurs parallel to higher density planes with low ].<ref>{{cite journal |last1=Vaknin |first1=Uriel |last2=Sherman |first2=Dov |last3=Gorfman |first3=Semën |title=Geometrical prediction of cleavage planes in crystal structures |journal=IUCrJ |date=1 September 2021 |volume=8 |issue=5 |pages=793–804 |doi=10.1107/S2052252521007272 |pmid=34584740 |url=https://journals.iucr.org/m/issues/2021/05/00/lt5039/lt5039.pdf |access-date=8 January 2025}}</ref> | ||
| ==References== | ==References== | ||
| {{reflist}} | {{reflist}} | ||
| <!--Wikidata item number Q3829754--> | <!--Wikidata item number Q3829754-->{{Crystallography}} | ||
| ] | ] | ||
| ] | ] | ||
| ] | |||
Latest revision as of 00:02, 10 January 2025
Law of crystallography
The law of constancy of interfacial angles (German: Das Gesetz der Winkelkonstanz; French: Loi de constance des angles) is an empirical law in the fields of crystallography and mineralogy concerning the shape, or morphology, of crystals. The law states that the angles between adjacent corresponding faces of crystals of a particular substance are always constant despite the different shapes, sizes, and mode of growth of crystals. The law is also named the first law of crystallography or Steno's law.
Definition

The International Union of Crystallography (IUCr) gives the following definition: "The law of the constancy of interfacial angles (or 'first law of crystallography') states that the angles between the crystal faces of a given species are constant, whatever the lateral extension of these faces and the origin of the crystal, and are characteristic of that species." The law is valid at constant temperature and pressure.
This law is important in identifying different mineral species as small changes in atomic structure can lead to large differences in the angles between crystal faces.
The sum of the interfacial angle (external angle) and the dihedral angle (internal angle) between two adjacent faces sharing a common edge is π radians (180°).
History

The law of the constancy of interfacial angles was first observed by the Danish physician Nicolas Steno when studying quartz crystals (De solido intra solidum naturaliter contento, Florence, 1669), who noted that, although the crystals differed in appearance from one to another, the angles between corresponding faces were always the same.
The law was also observed by Domenico Guglielmini (Riflessioni filosofiche dedotte dalle figure de Sali, Bologna, 1688), but it was generalized and firmly established by Jean-Baptiste Romé de l'Isle (Cristallographie, Paris, 1783) who accurately measured the interfacial angles of a great variety of crystals, using the goniometer designed by Arnould Carangeot and noted that the angles are characteristic of a substance. Carangeot was a student of Romé de L’Isle at the time of his invention of the basic crystallographic measuring instrument.
A French crystallographer, René Just Haüy, showed in 1774 that the known interfacial angles could be accounted for if the crystal were made up of minute building blocks (molécules intégrantes) that correspond approximately to the present-day unit cells.
In the diagram, the green dodecahedron on the left is built from cubical units, with the faces having a Miller index of (210). Unlike the regular dodecahedron on the right, its faces are not regular pentagons, but they are close to regular in appearance. The piling of the cubical units forms the pentagonal dodecahedron of pyritohedral pyrite. The decrement of the layers is in the proportion of 2:1, which leads to a dihedral angle at the top edge pq of 126° 87′, closely corresponding to that of the empirical crystal, of 127° 56′. The diagram is based on an 1801 drawing by René Just Haüy.
Crystal structure

The phenomenon of the constancy of interfacial angles is important because it is an outward sign of the inherent symmetry and ordered arrangement of atoms, ions or molecules within a crystal structure.
The angles between the various faces of a crystal remain unchanged throughout its growth. Crystals grow by addition of material to existing faces, this material being deposited parallel to the already existing surfaces. Consequently, if more material is added to one face than to another, the faces become unalike in size and shape, nevertheless the interfacial angles between them remain the same.
Crystals generally exhibit anisotropy, that is their properties are dependent on their direction. In particular, crystals cleave in specific directions, namely those parallel to the planes of the lattice structure. Cleavage preferentially occurs parallel to higher density planes with low Miller indices.
References
- "Law of the constancy of interfacial angles". Online Dictionary of Crystallography. International Union of Crystallography. 23 March 2019. Retrieved 7 January 2025.
- Borchardt-Ott, Walter (2012). Crystallography: An Introduction. Translated by Gould, Robert O. Berlin, Heidelberg: Springer. p. 35. doi:10.1007/978-3-642-16452-1. ISBN 9783642164514.
- Senechal, Marjorie (1990). "Brief history of geometrical crystallography". In Lima-de-Faria, J. (ed.). Historical atlas of crystallography. Dordrecht ; Boston: Published for International Union of Crystallography by Kluwer Academic Publishers. p. 44. ISBN 079230649X. Retrieved 24 December 2024.
- Schuh, Curtis P. "Steno, Nicolaus". Mineralogy and Crystallography: An Annotated Biobibliography of Books Published 1469 to 1919. Vol. 2. pp. 1381–1382. Archived from the original on 25 August 2007. Retrieved 8 January 2025.
- Steno, Nicolas (1669). De solido intra solidum naturaliter contento (in Latin). Florence: Star. Retrieved 8 January 2025.
- Steno, Nicolaus (1916) . The prodromus of Nicolaus Steno's dissertation concerning a solid body enclosed by process of nature within a solid. Translated by Winter, John Garrett. New York, London: The Macmillan Company. p. 272. Retrieved 9 January 2025.
Figures 5 and 6 belong to the class of those which I could present in countless numbers to prove that in the plane of the axis both the number and the length of the sides are changed in various ways without changing the angles.
- Ladd, Marcus Frederick Charles (2014). Symmetry of crystals and molecules. Oxford: Oxford University Press. pp. 13–15. ISBN 9780199670888.
- Romé de L'Isle, Jean Baptiste Louis de (1783). "Préface". Cristallographie (in French). Paris: De l'imprimerie de Monsieur. Retrieved 8 January 2025.
- Metzger, Hélène (1969) . La Gènese de la Science de Cristaux (in French). Paris: Albert Blanchard. pp. 67–68. Archived from the original on 2 October 2021. Retrieved 8 January 2025.
- Phillips, F. C. (1963). An Introduction To Crystallography (3rd ed.). New York: John Wiley & Sons. pp. 12–14. Retrieved 8 January 2025.
- Burke, John G. (1966). Origins of the science of crystals. Berkley and Los Angeles: University of California Press. pp. 69–70. Retrieved 8 January 2025.
- Scholz, Erhard (1989). Symmetrie, Gruppe, Dualität (in German). Basel Boston Berlin: Birkhäuser. pp. 19, 21. ISBN 3764319747.
- Authier, André (2015). "11.11 J.-B. L. Romé de l'Isle and the law of the constancy of interfacial angles, 1783". Early days of X-ray crystallography. Oxford: Oxford University Press. pp. 313–317. doi:10.1093/acprof:oso/9780199659845.003.0011. ISBN 9780198754053. Retrieved 8 January 2025.
- Haüy, René-Just (1784). Essai d'une théorie sur la structure des crystaux, appliquée à plusieurs genres de substances crystallisées (in French). Paris: Gogué et Née de La Rochelle. Archived from the original on 26 September 2016. Retrieved 8 January 2025.
- "Steno's law". Encyclopaedia Britannica. Retrieved 7 January 2025.
- Haüy, René Just (1801). Traité de minéralogie (in French). Vol. Caractère Minéralogique. Paris: Chez Louis. p. II, fig. 16. Retrieved 8 January 2025.
- Haüy, René Just (1822). Traité de cristallographie (in French). Vol. Atlas. Paris: Bachelier. p. 8, fig. 75. Retrieved 7 January 2025.
- Sunagawa, Ichirō (2007). Crystals: growth, morphology, and perfection. Cambridge: Cambridge University Press. ISBN 9780521841894.
- Hoffmann, Frank (2020). Introduction to crystallography (1st ed.). Cham, Switzerland: Springer. pp. 238–239. doi:10.1007/978-3-030-35110-6. ISBN 9783030351090.
- Vaknin, Uriel; Sherman, Dov; Gorfman, Semën (1 September 2021). "Geometrical prediction of cleavage planes in crystal structures" (PDF). IUCrJ. 8 (5): 793–804. doi:10.1107/S2052252521007272. PMID 34584740. Retrieved 8 January 2025.
| Crystallography | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Key concepts |
|  | ||||||||||
| Characterisation | ||||||||||||
| Algorithms | ||||||||||||
| Software | ||||||||||||
| Databases | ||||||||||||
| Journals | ||||||||||||
| Awards | ||||||||||||
| Organisation |
| |||||||||||