| Revision as of 03:22, 3 March 2010 edit71.36.27.41 (talk) →External links← Previous edit | Latest revision as of 12:21, 15 December 2024 edit undoD.Lazard (talk | contribs)Extended confirmed users33,829 edits Reverted 1 edit by Marsik84 (talk): WP:ELNO Also, original research, that is neither regularly published neither discuted in a reliably published secondary sourceTags: Twinkle Undo | ||
| Line 1: | Line 1: | ||
| {{short description|Ancient algorithm for generating prime numbers}} | |||
| ] | |||
| {{For|the sculpture|The Sieve of Eratosthenes (sculpture)}} | |||
| In ], the '''Sieve of Eratosthenes''' (Greek: κόσκινον Ἐρατοσθένους) is a simple, ancient ] for finding all ]s up to a specified integer.<ref>Horsley, Rev. Samuel, F. R. S., "''Κόσκινον Ερατοσθένους'' or, The Sieve of Eratosthenes. Being an Account of His Method of Finding All the Prime Numbers," ''Philosophical Transactions'' (1683-1775), Vol. 62. (1772), pp. 327-347.</ref> | |||
| ] | |||
| It works efficiently for the smaller primes (below 10 million).<ref>The Prime Glossary: "The Sieve of Eratosthenes", | |||
| http://primes.utm.edu/glossary/page.php?sort=SieveOfEratosthenes, references 16. November 2008.</ref> | |||
| It was created by ], an ] ]. However, none of his mathematical works survived - the sieve was described and attributed to Eratosthenes in the ''Introduction to Arithmetic'' by ].<ref> ], ''Introduction to Arithmetic'', I, 13. </ref> | |||
| In ], the '''sieve of Eratosthenes''' is an ancient ] for finding all ]s up to any given limit. | |||
| == Algorithm == | |||
| It does so by iteratively marking as ] (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with ] that is equal to that prime.<ref name="horsley">Horsley, Rev. Samuel, F. R. S., "''{{lang|el|Κόσκινον Ερατοσθένους}}'' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers," .</ref> This is the sieve's key distinction from using ] to sequentially test each candidate number for divisibility by each prime.<ref name="ONeill" /> Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. | |||
| A ] is a ] which has exactly two distinct natural number ]s: ] and itself. | |||
| The earliest known reference to the sieve ({{langx|grc|κόσκινον Ἐρατοσθένους}}, ''kóskinon Eratosthénous'') is in ]'s '']'',<ref name=nicomachus>{{citation|editor-first=Richard|editor-last=Hoche|editor-link=Richard Hoche|title=Nicomachi Geraseni Pythagorei Introductionis arithmeticae libri II, chapter XIII, 3|year=1866|location= Leipzig|publisher= B.G. Teubner|page=30|url=https://archive.org/stream/nicomachigerasen00nicouoft#page/30/mode/2up}}</ref> an early 2nd cent. CE book which attributes it to ], a 3rd cent. BCE ], though describing the sieving by odd numbers instead of by primes.<ref name=nicomachus1926>{{citation|author=Nicomachus of Gerasa|title=Introduction to Arithmetic; translated into English by Martin Luther D'Ooge; with studies in Greek arithmetic by Frank Egleston Robbins and Louis Charles Karpinski, chapter XIII, 3|year=1926|location=New York|publisher=The Macmillan Company|page=204}}</ref> | |||
| To find all the prime numbers less than or equal to a given integer ''n'' by Eratosthenes' method: | |||
| One of a number of ]s, it is one of the most efficient ways to find all of the smaller primes. It may be used to find primes in ]s.<ref>J. C. Morehead, "Extension of the Sieve of Eratosthenes to arithmetical progressions and applications", .</ref> | |||
| # Create a list of consecutive integers from two to ''n'': (2, 3, 4, ..., ''n''), | |||
| # Initially, let ''p'' equal 2, the first prime number, | |||
| # While enumerating all multiples of ''p'' starting from ''p''<sup>2</sup>, strike them off from the original list, | |||
| # Find the first number remaining on the list after ''p'' (it's the next prime); let ''p'' equal this number, | |||
| # Repeat steps 3 and 4 until ''p''<sup>2</sup> is greater than ''n''. | |||
| # All the remaining numbers in the list are prime. | |||
| == |
==Overview== | ||
| {{quote box|fontsize = 105%|''Sift the Two's and Sift the Three's:''<br />''The Sieve of Eratosthenes.''<br />''When the multiples sublime,''<br />''The numbers that remain are Prime.''|quoted=1|salign=center|source=Anonymous<ref>Clocksin, William F., Christopher S. Mellish, ''Programming in Prolog'', 1984, p. 170. {{isbn|3-540-11046-1}}.</ref>}} | |||
| A ] is a ] that has exactly two distinct natural number ]s: the number ] and itself. | |||
| To find all the prime numbers less than or equal to 30, proceed as follows: | |||
| To find all the prime numbers less than or equal to a given integer {{mvar|n}} by Eratosthenes' method: | |||
| <pre> | |||
| First generate a list of integers from 2 to 30: | |||
| # Create a list of consecutive integers from 2 through {{mvar|n}}: {{math|(2, 3, 4, ..., ''n'')}}. | |||
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | |||
| # Initially, let {{mvar|p}} equal 2, the smallest prime number. | |||
| # Enumerate the multiples of {{mvar|p}} by counting in increments of {{mvar|p}} from {{math|2''p''}} to {{mvar|n}}, and mark them in the list (these will be {{math|2''p'', 3''p'', 4''p'', ...}}; the {{mvar|p}} itself should not be marked). | |||
| # Find the smallest number in the list greater than {{mvar|p}} that is not marked. If there was no such number, stop. Otherwise, let {{mvar|p}} now equal this new number (which is the next prime), and repeat from step 3. | |||
| # When the algorithm terminates, the numbers remaining not marked in the list are all the primes below {{mvar|n}}. | |||
| The main idea here is that every value given to {{mvar|p}} will be prime, because if it were composite it would be marked as a multiple of some other, smaller prime. Note that some of the numbers may be marked more than once (e.g., 15 will be marked both for 3 and 5). | |||
| Strike out the multiples of 2 from the original list starting from 4, resulting in: | |||
| As a refinement, it is sufficient to mark the numbers in step 3 starting from {{math|''p''<sup>2</sup>}}, as all the smaller multiples of {{mvar|p}} will have already been marked at that point. This means that the algorithm is allowed to terminate in step 4 when {{math|''p''<sup>2</sup>}} is greater than {{mvar|n}}.<ref name="horsley" /> <!-- This does not appear in the algorithm as described by Nicomachus who instead describes sieving by odds, starting from the odd itself instead of its square.<ref name="nicomachus1926" /> --> | |||
| 2 3 5 7 9 11 13 15 17 19 21 23 25 27 29 | |||
| Another refinement is to initially list odd numbers only, {{math|(3, 5, ..., ''n'')}}, and count in increments of {{math|2''p''}} in step 3, thus marking only odd multiples of {{mvar|p}}. This actually appears in the original algorithm.<ref name="horsley" /><ref name="nicomachus1926" /> <!-- The table with divisors is probably not by Nicomachus. --> This can be generalized with ], forming the initial list only from numbers ] with the first few primes and not just from odds (i.e., numbers coprime with 2), and counting in the correspondingly adjusted increments so that only such multiples of {{mvar|p}} are generated that are coprime with those small primes, in the first place.<ref name="Runciman">{{Cite journal | doi = 10.1017/S0956796897002670| title = Functional Pearl: Lazy wheel sieves and spirals of primes| journal = Journal of Functional Programming| volume = 7| issue = 2| pages = 219–225| year = 1997| last1 = Runciman | first1 = Colin| s2cid = 2422563| url = http://eprints.whiterose.ac.uk/3784/1/runcimanc1.pdf}}</ref> | |||
| The first number in the list after 2 is 3; strike out the multiples of 3 from the | |||
| original list starting from 9, to get: | |||
| ===Example=== | |||
| 2 3 5 7 11 13 17 19 23 25 29 | |||
| To find all the prime numbers less than or equal to 30, proceed as follows. | |||
| First, generate a list of integers from 2 to 30: | |||
| The first number in the list after 3 is 5; strike out the multiples of 5 from the | |||
| original list starting from 25: | |||
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | |||
| The first number in the list after |
The first number in the list is 2; cross out every 2nd number in the list after 2 by counting up from 2 in increments of 2 (these will be all the multiples of 2 in the list): | ||
| than 30 so the process is finished. The final list consists of all the prime numbers | |||
| less than or equal to 30. | |||
| </pre> | |||
| 2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}} 9 {{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14</s>}} 15 {{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20</s>}} 21 {{gray|<s>22</s>}} 23 {{gray|<s>24</s>}} 25 {{gray|<s>26</s>}} 27 {{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | |||
| == Algorithm complexity and implementation == | |||
| The next number in the list after 2 is 3; cross out every 3rd number in the list after 3 by counting up from 3 in increments of 3 (these will be all the multiples of 3 in the list): | |||
| The crossing-off of multiples of each found prime number can be started at the square of the number, as lower multiples have already been crossed out during the previous steps. | |||
| 2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}}{{gray|<s> 9 </s>}}{{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14 </s>}}{{gray|<s>15 </s>}}{{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20 </s>}}{{gray|<s>21 </s>}}{{gray|<s>22</s>}} 23 {{gray|<s>24</s>}} 25 {{gray|<s>26 </s>}}{{gray|<s>27 </s>}}{{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | |||
| The ] of the algorithm is <math>O(n (\log n) (\log \log n))</math> bit operations with a memory requirement of <math>O(n)</math>.<ref>Pritchard, Paul, "Linear prime-number sieves: a family tree," ''Sci. Comput. Programming'' '''9''':1 (1987), pp. 17–35.</ref> Time complexity in ] model is <math>O(n \log \log n)</math> operations. The segmented version of the sieve of Eratosthenes, with basic optimizations, uses <math>O(n)</math> operations and <math>O(n^{1/2}\log\log n/\log n)</math> bits of memory.<ref>A. O. L. Atkin and D. J. Bernstein, , ''Mathematics of Computation'' '''73''' (2004), pp. 1023–1030.</ref> | |||
| The next number not yet crossed out in the list after 3 is 5; cross out every 5th number in the list after 5 by counting up from 5 in increments of 5 (i.e. all the multiples of 5): | |||
| ] suggested in 1975 that the primes sieve could be represented in a strikingly simple and elegant way in purely ].<ref>Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department | |||
| of Computational Science, University of St. Andrews 1975.</ref> Turner's sieve, which is more closely related to the Euler's sieve below, rendered in ], is: | |||
| 2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}}{{gray|<s> 9 </s>}}{{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14 </s>}}{{gray|<s>15 </s>}}{{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20 </s>}}{{gray|<s>21 </s>}}{{gray|<s>22</s>}} 23 {{gray|<s>24 </s>}}{{gray|<s>25 </s>}}{{gray|<s>26 </s>}}{{gray|<s>27 </s>}}{{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | |||
| <source lang="Haskell"> | |||
| primes = sieve | |||
| sieve (p : xs) = p : sieve | |||
| </source> | |||
| The next number not yet crossed out in the list after 5 is 7; the next step would be to cross out every 7th number in the list after 7, but they are all already crossed out at this point, as these numbers (14, 21, 28) are also multiples of smaller primes because 7 × 7 is greater than 30. The numbers not crossed out at this point in the list are all the prime numbers below 30: | |||
| Recently, ] showed that the complexity of Turner's algorithm is significantly | |||
| worse than the complexity of the classic ] renditions of the sieve.<ref>O'Neill, Melissa E., , Journal of Functional Programming, Published online by Cambridge University Press 09 Oct 2008 doi:10.1017/S0956796808007004.</ref> O'Neill demonstrated a ] based rendition of the sieve of Eratosthenes in Haskell with complexity similar to that of the classic imperative implementations. | |||
| 2 3 5 7 11 13 17 19 23 29 | |||
| ==Mnemonic== | |||
| ==Algorithm and variants== | |||
| A short, albeit imprecise, description of the Sieve of Erastosthenes in verse: | |||
| ===Pseudocode=== | |||
| The sieve of Eratosthenes can be expressed in ], as follows:<ref name="sedgewick">{{cite book | |||
| |last1=Sedgewick |first1=Robert |title=Algorithms in C++ | |||
| |publisher=Addison-Wesley |year=1992 |isbn=978-0-201-51059-1 | |||
| }}, p. 16.</ref><ref name="intro">, Computer Sciences Technical Report #909, Department of Computer Sciences University of Wisconsin-Madison, January 2, 1990 (the use of optimization of starting from squares, and thus using only the numbers whose square is below the upper limit, is shown).</ref> | |||
| '''algorithm''' Sieve of Eratosthenes '''is''' | |||
| {{cquote|''Sift the Twos and sift the Threes,''<br />''The Sieve of Eratosthenes.''<br />''When the multiples sublime,''<br />''The numbers that remain are Prime.''|||Traditional|<ref>{{cite web|url=http://c2.com/cgi/wiki?SieveOfEratosthenes|title=Sieve Of Eratosthenes|last=Merritt|first=Doug|date=December 14, 2008|accessdate=2009-03-26}}</ref><ref>{{cite web|url=http://www.cs.uku.fi/~mnykanen/FOH/lectures.pdf|title=An Introduction to Functional Programming with the Programming Language Haskell|last=Nyk¨anen|first=Matti|date=October 26, 2007|accessdate=2009-03-26}}</ref>}} | |||
| '''input''': an integer ''n'' > 1. | |||
| '''output''': all prime numbers from 2 through ''n''. | |||
| '''let''' ''A'' be an '''array of ]''' values, indexed by '''integer'''s 2 to ''n'', | |||
| initially all '''set''' to '''true'''. | |||
| '''for''' ''i'' = 2, 3, 4, ..., not exceeding {{math|''{{sqrt|n}}''}} '''do''' | |||
| '''if''' ''A'' '''is''' '''true''' | |||
| '''for''' ''j'' = ''i''<sup>2</sup>, ''i''<sup>2</sup>+''i'', ''i''<sup>2</sup>+2''i'', ''i''<sup>2</sup>+3''i'', ..., not exceeding ''n'' '''do''' | |||
| '''set''' ''A'' := '''false''' | |||
| '''return''' all ''i'' such that ''A'' '''is''' '''true'''. | |||
| This algorithm produces all primes not greater than {{mvar|n}}. It includes a common optimization, which is to start enumerating the multiples of each prime {{mvar|i}} from {{math|''i''<sup>2</sup>}}. The ] of this algorithm is {{math|''O''(''n'' log log ''n'')}},{{r|intro}} provided the array update is an {{math|''O''(1)}} operation, as is usually the case. | |||
| == Euler's Sieve == | |||
| ===Segmented sieve=== | |||
| Euler in his ] came up with a version of the sieve of Eratosthenes, better in the sense that each number was eliminated exactly once. Unlike Eratosthenes' sieve which strikes off multiples of primes it finds ''from the same sequence'', Euler's sieve works on sequences progressively culled from multiples of the preceding primes: | |||
| As Sorenson notes, the problem with the sieve of Eratosthenes is not the number of operations it performs but rather its memory requirements.{{r|intro}} For large {{mvar|n}}, the range of primes may not fit in memory; worse, even for moderate {{mvar|n}}, its ] use is highly suboptimal. The algorithm walks through the entire array {{mvar|A}}, exhibiting almost no ]. | |||
| A solution to these problems is offered by ''segmented'' sieves, where only portions of the range are sieved at a time.<ref>Crandall & Pomerance, ''Prime Numbers: A Computational Perspective'', second edition, Springer: 2005, pp. 121–24.</ref> These have been known since the 1970s, and work as follows:{{r|intro}}<ref>{{Cite journal | last1 = Bays | first1 = Carter | last2 = Hudson | first2 = Richard H. | year = 1977 | title = The segmented sieve of Eratosthenes and primes in arithmetic progressions to 10<sup>12</sup> | journal = BIT | volume = 17 | issue = 2 | pages = 121–127 | doi = 10.1007/BF01932283 | s2cid = 122592488 }}</ref> | |||
| <pre> | |||
| A) Start with all the natural numbers except '1' which is not a prime: | |||
| # Divide the range 2 through {{mvar|n}} into segments of some size {{math|Δ ≤ {{sqrt|''n''}}}}. | |||
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 ... | |||
| # Find the primes in the first (i.e. the lowest) segment, using the regular sieve. | |||
| ^ | |||
| # For each of the following segments, in increasing order, with {{mvar|m}} being the segment's topmost value, find the primes in it as follows: | |||
| ## Set up a Boolean array of size {{math|Δ}}. | |||
| ## Mark as non-prime the positions in the array corresponding to the multiples of each prime {{math|''p'' ≤ {{sqrt|''m''}}}} found so far, by enumerating its multiples in steps of {{math|''p''}} starting from the lowest multiple of {{math|''p''}} between {{math|{{mvar|m}} - Δ}} and {{mvar|m}}. | |||
| ## The remaining non-marked positions in the array correspond to the primes in the segment. It is not necessary to mark any multiples of ''these'' primes, because all of these primes are larger than {{math|{{sqrt|''m''}}}}, as for {{math|''k'' ≥ 1}}, one has <math>(k\Delta + 1)^2 > (k+1)\Delta</math>. | |||
| If {{math|Δ}} is chosen to be {{math|{{sqrt|''n''}}}}, the space complexity of the algorithm is {{math|''O''({{sqrt|''n''}})}}, while the time complexity is the same as that of the regular sieve.{{r|intro}} | |||
| B) The leftmost number is prime. Multiply each number in the list by this prime and | |||
| then discard the products: | |||
| For ranges with upper limit {{math|''n''}} so large that the sieving primes below {{math|{{sqrt|''n''}}}} as required by the page segmented sieve of Eratosthenes cannot fit in memory, a slower but much more space-efficient sieve like the pseudosquares prime sieve, developed by Jonathan P. Sorenson, can be used instead.<ref>J. Sorenson, , ''Proceedings of the 7th International Symposium on Algorithmic Number Theory''. (ANTS-VII, 2006).</ref> | |||
| (4 6 8 10 12 14 16 18 20 22 24 26 28 30 ... ) | |||
| ===Incremental sieve=== | |||
| These are removed: | |||
| An incremental formulation of the sieve<ref name="ONeill">O'Neill, Melissa E., , ''Journal of Functional Programming'', published online by Cambridge University Press 9 October 2008 {{doi|10.1017/S0956796808007004}}, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird).</ref> generates primes indefinitely (i.e., without an upper bound) by interleaving the generation of primes with the generation of their multiples (so that primes can be found in gaps between the multiples), where the multiples of each prime {{mvar|p}} are generated directly by counting up from the square of the prime in increments of {{mvar|p}} (or {{math|2''p''}} for odd primes). The generation must be initiated only when the prime's square is reached, to avoid adverse effects on efficiency. It can be expressed symbolically under the ] paradigm as | |||
| 4 6 8 10 12 14 16 18 20 22 24 26 28 30 | |||
| ''primes'' = \ for ''p'' in ''primes''], | |||
| These are left: | |||
| 2 3 5 7 9 11 13 15 17 19 21 23 25 27 29 ... | |||
| ^ | |||
| using ] notation with <code>\</code> denoting ] of ] of numbers. | |||
| C) The number after the previous prime is also a prime. Multiply by it each number | |||
| in the new list starting from this prime and then discard the products: | |||
| Primes can also be produced by iteratively sieving out the composites through ] by sequential primes, one prime at a time. It is not the sieve of Eratosthenes but is often confused with it, even though the sieve of Eratosthenes directly generates the composites instead of testing for them. Trial division has worse theoretical ] than that of the sieve of Eratosthenes in generating ranges of primes.<ref name="ONeill"/> | |||
| (9 15 21 27 33 39 45 51 57 63 69 75 81 87 ...) | |||
| When testing each prime, the ''optimal'' trial division algorithm uses all prime numbers not exceeding its square root, whereas the sieve of Eratosthenes produces each composite from its prime factors only, and gets the primes "for free", between the composites. The widely known 1975 ] sieve code by ]<ref>Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. (<syntaxhighlight lang="haskell" inline>primes = sieve ; sieve (p:nos) = p:sieve (remove (multsof p) nos); remove m = filter (not . m); multsof p n = rem n p==0</syntaxhighlight>). But see also , where we , attributed to P. Quarendon: <syntaxhighlight lang="python" inline>primeswrt = if car mod x=0 then primeswrt] else cons;primeswrt]] ; primes = cons;primes;cdr]]] ; primes]</syntaxhighlight>; the priority is unclear.</ref> is often presented as an example of the sieve of Eratosthenes<ref name="Runciman"/> but is actually a sub-optimal trial division sieve.<ref name="ONeill"/> | |||
| These are removed: | |||
| 9 15 21 27 | |||
| ==Algorithmic complexity== | |||
| These are left: | |||
| The sieve of Eratosthenes is a popular way to benchmark computer performance.<ref name="peng1985fall">{{cite news | url=https://archive.org/stream/byte-magazine-1985-11/1985_11_BYTE_10-11_Inside_the_IBM_PCs#page/n245/mode/2up | title=One Million Primes Through the Sieve | work=BYTE | date=Fall 1985 | access-date=19 March 2016 | author=Peng, T. A. | pages=243–244}}</ref> The ] of calculating all primes below {{mvar|n}} in the ] model is {{math|''O''(''n'' log log ''n'')}} operations, a direct consequence of the fact that the ] asymptotically approaches {{math|log log ''n''}}. It has an exponential time complexity with regard to length of the input, though, which makes it a ] algorithm. The basic algorithm requires {{math|''O''(''n'')}} of memory. | |||
| 2 3 5 7 11 13 17 19 23 25 29 ... | |||
| ^ | |||
| </pre> | |||
| Repeat C) indefinitely. On each repetition a new prime is identified (marked by the cursor, ^) until all the primes in the starting list have been found. | |||
| The ] of the algorithm is {{math|''O''<big>(</big>''n'' (log ''n'') (log log ''n'')<big>)</big>}} bit operations with a memory requirement of {{math|''O''(''n'')}}.<ref>Pritchard, Paul, "Linear prime-number sieves: a family tree," ''Sci. Comput. Programming'' '''9''':1 (1987), pp. 17–35.</ref> | |||
| Euler's sieve is thus naturally well suited to generating infinite sequences of prime numbers and Turner's sieve is a close rendition of it. Expressed in Haskell, it is: | |||
| <source lang="Haskell"> | |||
| import Data.OrdList (minus) | |||
| The normally implemented page segmented version has the same operational complexity of {{math|''O''(''n'' log log ''n'')}} as the non-segmented version but reduces the space requirements to the very minimal size of the segment page plus the memory required to store the base primes less than the square root of the range used to cull composites from successive page segments of size {{math|''O''<big><big>(</big></big>{{sfrac|{{sqrt|''n''}}|log ''n''}}<big><big>)</big></big>}}. | |||
| primes = euler | |||
| euler (p : xs) = p : euler (xs `minus` map (*p) (p : xs)) | |||
| </source> | |||
| A special (rarely, if ever, implemented) segmented version of the sieve of Eratosthenes, with basic optimizations, uses {{math|''O''(''n'')}} operations and {{math|''O''<big><big>(</big></big>{{sqrt|''n''}}{{sfrac|log log ''n''|log ''n''}}<big><big>)</big></big>}} bits of memory.<ref name="Pritchard1">Paul Pritchard, "A sublinear additive sieve for finding prime numbers", ''Communications of the ACM'' 24 (1981), 18–23. {{MR|600730}}</ref><ref name="Pritchard2">Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485. {{MR|685983}}</ref><ref name="Pritchard3">Paul Pritchard, "Fast compact prime number sieves" (among others), ''Journal of Algorithms'' 4 | |||
| Comparing this algorithm with ], the primes to the left of the cursor correspond to factors in the left hand side of the equation at each stage of the sifting, whereas the sequence to the right and including the cursor correspond to the series on the right hand side of the equation at each stage (minus the initial one). | |||
| (1983), 332–344. {{MR|729229}}</ref> | |||
| Using ] ignores constant factors and offsets that may be very significant for practical ranges: The sieve of Eratosthenes variation known as the Pritchard wheel sieve<ref name="Pritchard1" /><ref name="Pritchard2" /><ref name="Pritchard3" /> has an {{math|''O''(''n'')}} performance, but its basic implementation requires either a "one large array" algorithm which limits its usable range to the amount of available memory else it needs to be page segmented to reduce memory use. When implemented with page segmentation in order to save memory, the basic algorithm still requires about {{math|''O''<big><big>(</big></big>{{sfrac|''n''|log ''n''}}<big><big>)</big></big>}} bits of memory (much more than the requirement of the basic page segmented sieve of Eratosthenes using {{math|''O''<big><big>(</big></big>{{sfrac|{{sqrt|''n''}}|log ''n''}}<big><big>)</big></big>}} bits of memory). Pritchard's work reduced the memory requirement at the cost of a large constant factor. Although the resulting wheel sieve has {{math|''O''(''n'')}} performance and an acceptable memory requirement, it is not faster than a reasonably Wheel Factorized basic sieve of Eratosthenes for practical sieving ranges. | |||
| When generating only a finite sequence of primes, when we have exceeded the square root of the upper limit of our range, we have the desired sequence of prime numbers. In the example given above that will be achieved when we identify the prime ''7'', to give our list of all primes less than or equal to ''30''. | |||
| ==Euler's sieve== | |||
| Euler's ] contains a version of the sieve of Eratosthenes in which each composite number is eliminated exactly once.<ref name="intro" /> The same sieve was rediscovered and observed to take ] by {{harvtxt|Gries|Misra|1978}}.<ref>{{citation | |||
| | last1 = Gries | first1 = David | author1-link = David Gries | |||
| | last2 = Misra | first2 = Jayadev | |||
| | date = December 1978 | |||
| | doi = 10.1145/359657.359660 | |||
| | issue = 12 | |||
| | journal = ] | |||
| | pages = 999–1003 | |||
| | title = A linear sieve algorithm for finding prime numbers | |||
| | volume = 21| hdl = 1813/6407 | s2cid = 11990373 | url = https://ecommons.cornell.edu/bitstream/1813/6407/1/77-313.pdf | |||
| | hdl-access = free | |||
| }}.</ref> It, too, starts with a ] of numbers from 2 to {{mvar|n}} in order. On each step the first element is identified as the next prime, is multiplied with each element of the list (thus starting with itself), and the results are marked in the list for subsequent deletion. The initial element and the marked elements are then removed from the working sequence, and the process is repeated: | |||
| <div style="font-size:85%;"> <!-- these s are put here hoping to prevent bots messing it up --> | |||
| (3) 5 7 <u>9</u> 11 13 <u>15</u> 17 19 <u>21</u> 23 25 <u>27</u> 29 31 <u>33</u> 35 37 <u>39</u> 41 43 <u>45</u> 47 49 <u>51</u> 53 55 <u>57</u> 59 61 <u>63</u> 65 67 <u>69</u> 71 73 <u>75</u> 77 79 ... | |||
| (5) 7 11 13 17 19 23 <u>25</u> 29 31 <u>35</u> 37 41 43 47 49 53 <u>55</u> 59 61 <u>65</u> 67 71 73 77 79 ... | |||
| (7) 11 13 17 19 23 29 31 37 41 43 47 <u>49</u> 53 59 61 67 71 73 <u>77</u> 79 ... | |||
| (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ... | |||
| | |||
| </div> | |||
| Here the example is shown starting from odds, after the first step of the algorithm. Thus, on the {{mvar|k}}th step all the remaining multiples of the {{mvar|k}}th prime are removed from the list, which will thereafter contain only numbers coprime with the first {{mvar|k}} primes (cf. ]), so that the list will start with the next prime, and all the numbers in it below the square of its first element will be prime too. | |||
| Thus, when generating a bounded sequence of primes, when the next identified prime exceeds the square root of the upper limit, all the remaining numbers in the list are prime.<ref name="intro" /> In the example given above that is achieved on identifying 11 as next prime, giving a list of all primes less than or equal to 80. | |||
| Note that numbers that will be discarded by a step are still used while marking the multiples in that step, e.g., for the multiples of 3 it is {{nowrap|1=3 × 3 = 9}}, {{nowrap|1=3 × 5 = 15}}, {{nowrap|1=3 × 7 = 21}}, {{nowrap|1=3 × '''''9''''' = 27}}, ..., {{nowrap|1=3 × '''''15''''' = 45}}, ..., so care must be taken dealing with this.<ref name="intro" /> | |||
| ==See also== | ==See also== | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| ==References== | ==References== | ||
| {{ |
{{Reflist|2}} | ||
| ==External links== | ==External links== | ||
| * | |||
| * | |||
| * | |||
| * | * | ||
| * by George Beck, ]. | * by George Beck, ]. | ||
| * | * | ||
| * | * | ||
| * | |||
| * | |||
| * | |||
| * | |||
| * Sieve of Eratosthenes in C from 1998 with nice features and algorithmic tricks explained. | |||
| <!--spacing--> | |||
| {{number theoretic algorithms}} | {{number theoretic algorithms}} | ||
| {{DEFAULTSORT:Sieve Of Eratosthenes}} | |||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 12:21, 15 December 2024
Ancient algorithm for generating prime numbers For the sculpture, see The Sieve of Eratosthenes (sculpture).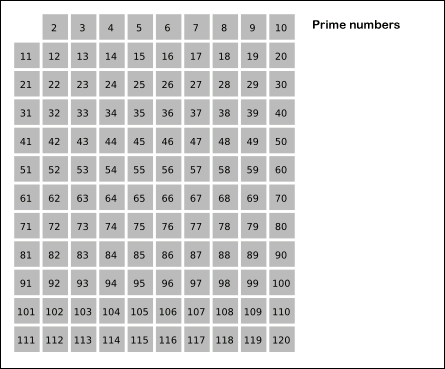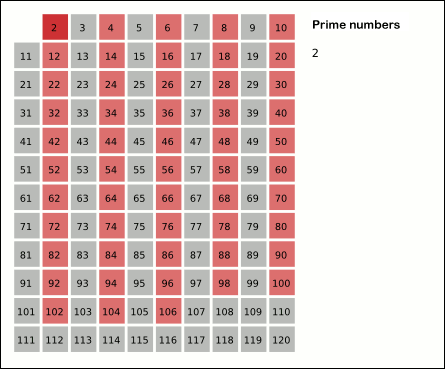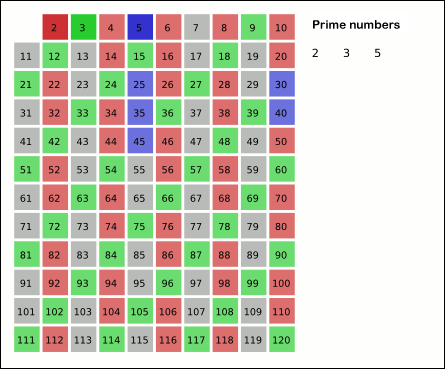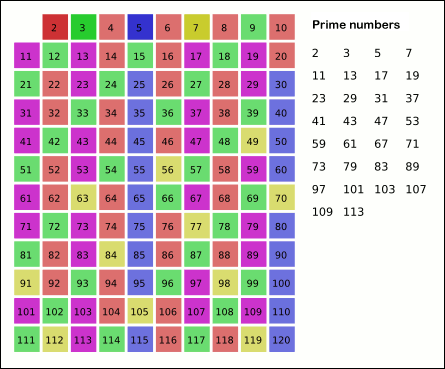
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit.
It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with constant difference between them that is equal to that prime. This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes.
The earliest known reference to the sieve (Ancient Greek: κόσκινον Ἐρατοσθένους, kóskinon Eratosthénous) is in Nicomachus of Gerasa's Introduction to Arithmetic, an early 2nd cent. CE book which attributes it to Eratosthenes of Cyrene, a 3rd cent. BCE Greek mathematician, though describing the sieving by odd numbers instead of by primes.
One of a number of prime number sieves, it is one of the most efficient ways to find all of the smaller primes. It may be used to find primes in arithmetic progressions.
Overview
AnonymousSift the Two's and Sift the Three's:
The Sieve of Eratosthenes.
When the multiples sublime,
The numbers that remain are Prime.
A prime number is a natural number that has exactly two distinct natural number divisors: the number 1 and itself.
To find all the prime numbers less than or equal to a given integer n by Eratosthenes' method:
- Create a list of consecutive integers from 2 through n: (2, 3, 4, ..., n).
- Initially, let p equal 2, the smallest prime number.
- Enumerate the multiples of p by counting in increments of p from 2p to n, and mark them in the list (these will be 2p, 3p, 4p, ...; the p itself should not be marked).
- Find the smallest number in the list greater than p that is not marked. If there was no such number, stop. Otherwise, let p now equal this new number (which is the next prime), and repeat from step 3.
- When the algorithm terminates, the numbers remaining not marked in the list are all the primes below n.
The main idea here is that every value given to p will be prime, because if it were composite it would be marked as a multiple of some other, smaller prime. Note that some of the numbers may be marked more than once (e.g., 15 will be marked both for 3 and 5).
As a refinement, it is sufficient to mark the numbers in step 3 starting from p, as all the smaller multiples of p will have already been marked at that point. This means that the algorithm is allowed to terminate in step 4 when p is greater than n.
Another refinement is to initially list odd numbers only, (3, 5, ..., n), and count in increments of 2p in step 3, thus marking only odd multiples of p. This actually appears in the original algorithm. This can be generalized with wheel factorization, forming the initial list only from numbers coprime with the first few primes and not just from odds (i.e., numbers coprime with 2), and counting in the correspondingly adjusted increments so that only such multiples of p are generated that are coprime with those small primes, in the first place.
Example
To find all the prime numbers less than or equal to 30, proceed as follows.
First, generate a list of integers from 2 to 30:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
The first number in the list is 2; cross out every 2nd number in the list after 2 by counting up from 2 in increments of 2 (these will be all the multiples of 2 in the list):
2 3456789101112131415161718192021222324252627282930
The next number in the list after 2 is 3; cross out every 3rd number in the list after 3 by counting up from 3 in increments of 3 (these will be all the multiples of 3 in the list):
2 3456789101112131415161718192021222324252627282930
The next number not yet crossed out in the list after 3 is 5; cross out every 5th number in the list after 5 by counting up from 5 in increments of 5 (i.e. all the multiples of 5):
2 3456789101112131415161718192021222324252627282930
The next number not yet crossed out in the list after 5 is 7; the next step would be to cross out every 7th number in the list after 7, but they are all already crossed out at this point, as these numbers (14, 21, 28) are also multiples of smaller primes because 7 × 7 is greater than 30. The numbers not crossed out at this point in the list are all the prime numbers below 30:
2 3 5 7 11 13 17 19 23 29
Algorithm and variants
Pseudocode
The sieve of Eratosthenes can be expressed in pseudocode, as follows:
algorithm Sieve of Eratosthenes is
input: an integer n > 1.
output: all prime numbers from 2 through n.
let A be an array of Boolean values, indexed by integers 2 to n,
initially all set to true.
for i = 2, 3, 4, ..., not exceeding √n do
if A is true
for j = i, i+i, i+2i, i+3i, ..., not exceeding n do
set A := false
return all i such that A is true.
This algorithm produces all primes not greater than n. It includes a common optimization, which is to start enumerating the multiples of each prime i from i. The time complexity of this algorithm is O(n log log n), provided the array update is an O(1) operation, as is usually the case.
Segmented sieve
As Sorenson notes, the problem with the sieve of Eratosthenes is not the number of operations it performs but rather its memory requirements. For large n, the range of primes may not fit in memory; worse, even for moderate n, its cache use is highly suboptimal. The algorithm walks through the entire array A, exhibiting almost no locality of reference.
A solution to these problems is offered by segmented sieves, where only portions of the range are sieved at a time. These have been known since the 1970s, and work as follows:
- Divide the range 2 through n into segments of some size Δ ≤ √n.
- Find the primes in the first (i.e. the lowest) segment, using the regular sieve.
- For each of the following segments, in increasing order, with m being the segment's topmost value, find the primes in it as follows:
- Set up a Boolean array of size Δ.
- Mark as non-prime the positions in the array corresponding to the multiples of each prime p ≤ √m found so far, by enumerating its multiples in steps of p starting from the lowest multiple of p between m - Δ and m.
- The remaining non-marked positions in the array correspond to the primes in the segment. It is not necessary to mark any multiples of these primes, because all of these primes are larger than √m, as for k ≥ 1, one has .
If Δ is chosen to be √n, the space complexity of the algorithm is O(√n), while the time complexity is the same as that of the regular sieve.
For ranges with upper limit n so large that the sieving primes below √n as required by the page segmented sieve of Eratosthenes cannot fit in memory, a slower but much more space-efficient sieve like the pseudosquares prime sieve, developed by Jonathan P. Sorenson, can be used instead.
Incremental sieve
An incremental formulation of the sieve generates primes indefinitely (i.e., without an upper bound) by interleaving the generation of primes with the generation of their multiples (so that primes can be found in gaps between the multiples), where the multiples of each prime p are generated directly by counting up from the square of the prime in increments of p (or 2p for odd primes). The generation must be initiated only when the prime's square is reached, to avoid adverse effects on efficiency. It can be expressed symbolically under the dataflow paradigm as
primes = \ for p in primes],
using list comprehension notation with \ denoting set subtraction of arithmetic progressions of numbers.
Primes can also be produced by iteratively sieving out the composites through divisibility testing by sequential primes, one prime at a time. It is not the sieve of Eratosthenes but is often confused with it, even though the sieve of Eratosthenes directly generates the composites instead of testing for them. Trial division has worse theoretical complexity than that of the sieve of Eratosthenes in generating ranges of primes.
When testing each prime, the optimal trial division algorithm uses all prime numbers not exceeding its square root, whereas the sieve of Eratosthenes produces each composite from its prime factors only, and gets the primes "for free", between the composites. The widely known 1975 functional sieve code by David Turner is often presented as an example of the sieve of Eratosthenes but is actually a sub-optimal trial division sieve.
Algorithmic complexity
The sieve of Eratosthenes is a popular way to benchmark computer performance. The time complexity of calculating all primes below n in the random access machine model is O(n log log n) operations, a direct consequence of the fact that the prime harmonic series asymptotically approaches log log n. It has an exponential time complexity with regard to length of the input, though, which makes it a pseudo-polynomial algorithm. The basic algorithm requires O(n) of memory.
The bit complexity of the algorithm is O(n (log n) (log log n)) bit operations with a memory requirement of O(n).
The normally implemented page segmented version has the same operational complexity of O(n log log n) as the non-segmented version but reduces the space requirements to the very minimal size of the segment page plus the memory required to store the base primes less than the square root of the range used to cull composites from successive page segments of size O(√n/log n).
A special (rarely, if ever, implemented) segmented version of the sieve of Eratosthenes, with basic optimizations, uses O(n) operations and O(√nlog log n/log n) bits of memory.
Using big O notation ignores constant factors and offsets that may be very significant for practical ranges: The sieve of Eratosthenes variation known as the Pritchard wheel sieve has an O(n) performance, but its basic implementation requires either a "one large array" algorithm which limits its usable range to the amount of available memory else it needs to be page segmented to reduce memory use. When implemented with page segmentation in order to save memory, the basic algorithm still requires about O(n/log n) bits of memory (much more than the requirement of the basic page segmented sieve of Eratosthenes using O(√n/log n) bits of memory). Pritchard's work reduced the memory requirement at the cost of a large constant factor. Although the resulting wheel sieve has O(n) performance and an acceptable memory requirement, it is not faster than a reasonably Wheel Factorized basic sieve of Eratosthenes for practical sieving ranges.
Euler's sieve
Euler's proof of the zeta product formula contains a version of the sieve of Eratosthenes in which each composite number is eliminated exactly once. The same sieve was rediscovered and observed to take linear time by Gries & Misra (1978). It, too, starts with a list of numbers from 2 to n in order. On each step the first element is identified as the next prime, is multiplied with each element of the list (thus starting with itself), and the results are marked in the list for subsequent deletion. The initial element and the marked elements are then removed from the working sequence, and the process is repeated:
(3) 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 ... (5) 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 ... (7) 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 ... (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ...
Here the example is shown starting from odds, after the first step of the algorithm. Thus, on the kth step all the remaining multiples of the kth prime are removed from the list, which will thereafter contain only numbers coprime with the first k primes (cf. wheel factorization), so that the list will start with the next prime, and all the numbers in it below the square of its first element will be prime too.
Thus, when generating a bounded sequence of primes, when the next identified prime exceeds the square root of the upper limit, all the remaining numbers in the list are prime. In the example given above that is achieved on identifying 11 as next prime, giving a list of all primes less than or equal to 80.
Note that numbers that will be discarded by a step are still used while marking the multiples in that step, e.g., for the multiples of 3 it is 3 × 3 = 9, 3 × 5 = 15, 3 × 7 = 21, 3 × 9 = 27, ..., 3 × 15 = 45, ..., so care must be taken dealing with this.
See also
References
- ^ Horsley, Rev. Samuel, F. R. S., "Κόσκινον Ερατοσθένους or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers," Philosophical Transactions (1683–1775), Vol. 62. (1772), pp. 327–347.
- ^ O'Neill, Melissa E., "The Genuine Sieve of Eratosthenes", Journal of Functional Programming, published online by Cambridge University Press 9 October 2008 doi:10.1017/S0956796808007004, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird).
- Hoche, Richard, ed. (1866), Nicomachi Geraseni Pythagorei Introductionis arithmeticae libri II, chapter XIII, 3, Leipzig: B.G. Teubner, p. 30
- ^ Nicomachus of Gerasa (1926), Introduction to Arithmetic; translated into English by Martin Luther D'Ooge; with studies in Greek arithmetic by Frank Egleston Robbins and Louis Charles Karpinski, chapter XIII, 3, New York: The Macmillan Company, p. 204
- J. C. Morehead, "Extension of the Sieve of Eratosthenes to arithmetical progressions and applications", Annals of Mathematics, Second Series 10:2 (1909), pp. 88–104.
- Clocksin, William F., Christopher S. Mellish, Programming in Prolog, 1984, p. 170. ISBN 3-540-11046-1.
- ^ Runciman, Colin (1997). "Functional Pearl: Lazy wheel sieves and spirals of primes" (PDF). Journal of Functional Programming. 7 (2): 219–225. doi:10.1017/S0956796897002670. S2CID 2422563.
- Sedgewick, Robert (1992). Algorithms in C++. Addison-Wesley. ISBN 978-0-201-51059-1., p. 16.
- ^ Jonathan Sorenson, An Introduction to Prime Number Sieves, Computer Sciences Technical Report #909, Department of Computer Sciences University of Wisconsin-Madison, January 2, 1990 (the use of optimization of starting from squares, and thus using only the numbers whose square is below the upper limit, is shown).
- Crandall & Pomerance, Prime Numbers: A Computational Perspective, second edition, Springer: 2005, pp. 121–24.
- Bays, Carter; Hudson, Richard H. (1977). "The segmented sieve of Eratosthenes and primes in arithmetic progressions to 10". BIT. 17 (2): 121–127. doi:10.1007/BF01932283. S2CID 122592488.
- J. Sorenson, "The pseudosquares prime sieve", Proceedings of the 7th International Symposium on Algorithmic Number Theory. (ANTS-VII, 2006).
- Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. (
primes = sieve ; sieve (p:nos) = p:sieve (remove (multsof p) nos); remove m = filter (not . m); multsof p n = rem n p==0). But see also Peter Henderson, Morris, James Jr., A Lazy Evaluator, 1976, where we find the following, attributed to P. Quarendon:primeswrt = if car mod x=0 then primeswrt] else cons;primeswrt]] ; primes = cons;primes;cdr]]] ; primes]; the priority is unclear. - Peng, T. A. (Fall 1985). "One Million Primes Through the Sieve". BYTE. pp. 243–244. Retrieved 19 March 2016.
- Pritchard, Paul, "Linear prime-number sieves: a family tree," Sci. Comput. Programming 9:1 (1987), pp. 17–35.
- ^ Paul Pritchard, "A sublinear additive sieve for finding prime numbers", Communications of the ACM 24 (1981), 18–23. MR600730
- ^ Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485. MR685983
- ^ Paul Pritchard, "Fast compact prime number sieves" (among others), Journal of Algorithms 4 (1983), 332–344. MR729229
- Gries, David; Misra, Jayadev (December 1978), "A linear sieve algorithm for finding prime numbers" (PDF), Communications of the ACM, 21 (12): 999–1003, doi:10.1145/359657.359660, hdl:1813/6407, S2CID 11990373.
External links
- primesieve – Very fast highly optimized C/C++ segmented Sieve of Eratosthenes
- Eratosthenes, sieve of at Encyclopaedia of Mathematics
- Interactive JavaScript Page
- Sieve of Eratosthenes by George Beck, Wolfram Demonstrations Project.
- Sieve of Eratosthenes in Haskell
- Sieve of Eratosthenes algorithm illustrated and explained. Java and C++ implementations.
- A related sieve written in x86 assembly language
- Fast optimized highly parallel CUDA segmented Sieve of Eratosthenes in C
- SieveOfEratosthenesInManyProgrammingLanguages c2 wiki page
- The Art of Prime Sieving Sieve of Eratosthenes in C from 1998 with nice features and algorithmic tricks explained.
| Number-theoretic algorithms | |
|---|---|
| Primality tests | |
| Prime-generating | |
| Integer factorization | |
| Multiplication | |
| Euclidean division | |
| Discrete logarithm | |
| Greatest common divisor | |
| Modular square root | |
| Other algorithms | |
| |
 .
.