| Revision as of 01:47, 18 March 2010 editRHB100 (talk | contribs)Extended confirmed users2,197 edits →Mathematical form: clarified diagram← Previous edit | Latest revision as of 13:05, 28 September 2024 edit undo178.138.97.179 (talk) conservative vector fields | ||
| (469 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Fundamental study of potential theory}} | |||
| ]s of the cross-section are at the surface of the body.]] | |||
| {{redirect|Gravity potential|Earth's gravity potential|Geopotential|the field of gravity potentials|Gravitational field}} | |||
| In ], the '''gravitational potential''' at a location represents the ] (]) per unit mass as an object moves to that location from a reference location. It is analogous to the ] with ] playing the role of ]. By convention, the gravitational potential is defined as zero infinitely far away from any mass. As a result it is negative elsewhere. | |||
| In ], the '''gravitational potential''' is a ] associating with each point in space the ] (] transferred) per unit mass that would be needed to move an object to that point from a fixed reference point in the conservative ]. It is ] to the ] with ] playing the role of ]. The reference point, where the potential is zero, is by convention ] far away from any mass, resulting in a negative potential at any ] distance. Their similarity is correlated with both associated ] having ]s. | |||
| In mathematics the gravitational potential is also known as the ] and is fundamental in the study of ]. | |||
| Mathematically, the gravitational potential is also known as the ] and is fundamental in the study of ]. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies.<ref>{{cite book|title=Electrostatics and magnetostatics of polarized ellipsoidal bodies: the depolarization tensor method|first1=C.E.|last1=Solivérez|edition=1st English|year=2016|publisher=Free Scientific Information| isbn=978-987-28304-0-3}}</ref> | |||
| ==Potential energy== | ==Potential energy== | ||
| {{main|Gravitational potential energy}} | |||
| The gravitational potential (''V'') is the ] (''U'') per unit mass: | |||
| The gravitational potential (''V'') at a location is the gravitational ] (''U'') at that location per unit mass: | |||
| <math display="block">V = \frac{U}{m},</math> | |||
| where ''m'' is the mass of the object. |
where ''m'' is the mass of the object. Potential energy is equal (in magnitude, but negative) to the work done by the gravitational field moving a body to its given position in space from infinity. If the body has a mass of 1 kilogram, then the potential energy to be assigned to that body is equal to the gravitational potential. So the potential can be interpreted as the negative of the work done by the gravitational field moving a unit mass in from infinity. | ||
| In some situations the equations can be simplified by assuming a field |
In some situations, the equations can be simplified by assuming a field that is nearly independent of position. For instance, in a region close to the surface of the Earth, the ], ''g'', can be considered constant. In that case, the difference in potential energy from one height to another is, to a good approximation, linearly related to the difference in height: | ||
| <math display="block">\Delta U \approx mg \Delta h.</math> | |||
| ==Mathematical form== | ==Mathematical form== | ||
| The gravitational ] ''V'' at a distance ''x'' from a ] of mass ''M'' can be defined as the work ''W'' that needs to be done by an external agent to bring a unit mass in from infinity to that point:<ref>{{cite book|title=Classical Dynamics of particles and systems|first1=J.B.|last1=Marion|first2=S.T.|last2=Thornton| edition=4th|page=|year=1995|publisher=Harcourt Brace & Company |isbn=0-03-097302-3|url-access=registration|url=https://archive.org/details/classicaldynamic00mari_0/page/192}}</ref><ref>{{cite book |title=Mathematical Methods For Physicists International Student Edition |edition=6th |first1=George B. |last1=Arfken |first2=Hans J. |last2=Weber |publisher=] |year=2005 |isbn=978-0-08-047069-6 |page=72 |url=https://books.google.com/books?id=tNtijk2iBSMC&pg=PA72}}</ref><ref>{{cite book |title=Cambridge International AS and A Level Physics Coursebook |edition=illustrated |first1=David |last1=Sang |first2=Graham |last2=Jones |first3=Gurinder |last3=Chadha |first4=Richard |last4=Woodside |first5=Will |last5=Stark |first6=Aidan |last6=Gill |publisher=] |year=2014 |isbn=978-1-107-69769-0 |page=276 |url=https://books.google.com/books?id=SjsDBAAAQBAJ&pg=PA276}}</ref><ref>{{cite book |title=A-level Physics |edition=illustrated |first1=Roger |last1=Muncaster |publisher=] |year=1993 |isbn=978-0-7487-1584-8 |page=106 |url=https://books.google.com/books?id=Knov8XAyf2cC&pg=PA106}}</ref> | |||
| The ] ''V'' at a distance ''x'' from a ] of mass ''M'' is | |||
| :<math>V = -\frac{GM}{x},</math> | |||
| where ''G'' is the ]. The potential has units of energy per unit mass; e.g., J/kg in the ] system. By convention, it is always negative where it is defined, and as ''r'' tends to infinity, it approaches zero. | |||
| <math display="block">V(\mathbf{x}) = \frac{W}{m} = \frac{1}{m} \int_{\infty}^{x} \mathbf{F} \cdot d\mathbf{x} = \frac{1}{m} \int_{\infty}^{x} \frac{G m M}{x^2} dx = -\frac{G M}{x},</math> | |||
| The ], and thus the acceleration of a small body in the space around the massive object, is the negative ] of the gravitational potential. Because the potential has no angular components, its gradient is: | |||
| where ''G'' is the ], and '''F''' is the gravitational force. The product ''GM'' is the ] and is often known to higher precision than ''G'' or ''M'' separately. The potential has units of energy per mass, e.g., J/kg in the ] system. By convention, it is always negative where it is defined, and as ''x'' tends to infinity, it approaches zero. | |||
| :<math>\mathbf{a} = -\frac{GM}{x^3} \mathbf{x} = -\frac{GM}{x^2} \hat{\mathbf{x}},</math> | |||
| where '''x''' is a vector of length ''x'' pointing from the point mass towards the small body and <math>\hat{\mathbf{x}}</math> is a unit vector pointing from the point mass towards the small body. The magnitude of the acceleration therefore follows an ]: | |||
| :<math>|\mathbf{a}| = \frac{GM}{x^2}.</math> | |||
| The ], and thus the acceleration of a small body in the space around the massive object, is the negative ] of the gravitational potential. Thus the negative of a negative gradient yields positive acceleration toward a massive object. Because the potential has no angular components, its gradient is | |||
| The potential associated with a ] is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points '''x'''<sub>1</sub>, ..., '''x'''<sub>''n''</sub> and have masses ''m''<sub>1</sub>, ..., ''m''<sub>''n''</sub>, then the potential of the distribution at the point '''x''' is: | |||
| <math display="block">\mathbf{a} = -\frac{GM}{x^3} \mathbf{x} = -\frac{GM}{x^2} \hat{\mathbf{x}},</math> | |||
| where '''x''' is a vector of length ''x'' pointing from the point mass toward the small body and <math>\hat{\mathbf{x}}</math> is a unit vector pointing from the point mass toward the small body. The magnitude of the acceleration therefore follows an ]: | |||
| In the vector diagram, '''cm''' denotes the point mass and '''px''' denotes the point at which the potential is being computed. | |||
| <math display="block">\|\mathbf{a}\| = \frac{GM}{x^2}.</math> | |||
| ] | |||
| If the mass distribution is given as a mass ] ''dm'' on three-dimensional ] '''R'''<sup>3</sup>, then the potential is the ] of −G/|'''y'''| with ''dm''.<ref>{{harvnb|Vladimirov|1984|loc=§7.8}}</ref> In good cases this equals the ] | |||
| :<math>V(\mathbf{x}) = -\int_{\mathbf{R}^3} \frac{G}{|\mathbf{x} - \mathbf{r}|}\,dm(\mathbf{r}).</math> | |||
| If there is a function ''ρ''('''r''') representing the density of the distribution at '''r''', so that {{nowrap begin}}''dm''('''r''') = ''ρ''('''r''')''dv''<!-- <sup> 3</sup>'''r''' -->{{nowrap end}}, where ''dv''<!-- <sup> 3</sup>'''r''' --> is the Euclidean ], then the gravitational potential is | |||
| :<math>V(\mathbf{x}) = -\int_{\mathbf{R}^3} \frac{G}{|\mathbf{x}-\mathbf{r}|}\,\rho(\mathbf{r})dv \, .</math> | |||
| The potential associated with a ] is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points '''x'''<sub>1</sub>, ..., '''x'''<sub>''n''</sub> and have masses ''m''<sub>1</sub>, ..., ''m''<sub>''n''</sub>, then the potential of the distribution at the point '''x''' is | |||
| If ''V'' is a potential function coming from a continuous mass distribution ''ρ''('''r'''), then ''ρ'' can be recovered using the ] Δ using the formula: | |||
| <math display="block">V(\mathbf{x}) = \sum_{i=1}^n -\frac{Gm_i}{\|\mathbf{x} - \mathbf{x}_i\|}.</math> | |||
| This holds pointwise whenever ''ρ'' is continuous and is zero outside of a bounded set. In general, the mass measure ''dm'' can be recovered in the same way if the Laplace operator is taken in the sense of ]s. Consequently the gravitational potential satisfies ]. See also ] and ]. | |||
| ] | |||
| ==Spherical symmetry== | |||
| A spherically symmetric mass distribution behaves to an observer completely outside the distribution as though all of the mass were concentrated at the center, and thus effectively as a ], by the ]. On the surface of the Earth, the acceleration is given by so-called ] ''g'', approximately 9.8 m/s<sup>2</sup>, although this value varies slightly with latitude and altitude: the magnitude of the acceleration is a little larger at the poles than at the equator because the Earth is an ]. | |||
| If the mass distribution is given as a mass ] ''dm'' on three-dimensional ] '''R'''<sup>3</sup>, then the potential is the ] of {{math|−''G''/{{abs|'''r'''}}}} with ''dm''.{{Citation needed|date=May 2023}} In good cases{{clarify|date=September 2020}} this equals the integral | |||
| Within a spherically symmetric mass distribution, it is possible to solve ]. Within a uniform spherical body of radius ''R'' and density σ, the gravitational force ''g'' inside the sphere varies linearly with distance ''r'' from the center, giving the gravitational potential inside the sphere, which is<ref>{{harvnb|Marion|Thornton|2003|loc=§5.2}}</ref> | |||
| <math display="block">V(\mathbf{x}) = -\int_{\R^3} \frac{G}{\|\mathbf{x} - \mathbf{r}\|}\,dm(\mathbf{r}),</math> | |||
| where {{math|{{abs|'''x''' − '''r'''}}}} is the ] between the points '''x''' and '''r'''. If there is a function ''ρ''('''r''') representing the density of the distribution at '''r''', so that {{math|1=''dm''('''r''') = ''ρ''('''r''') ''dv''('''r''')}}, where ''dv''('''r''') is the Euclidean ], then the gravitational potential is the ] | |||
| <math display="block">V(\mathbf{x}) = -\int_{\R^3} \frac{G}{\|\mathbf{x}-\mathbf{r}\|}\,\rho(\mathbf{r})dv(\mathbf{r}).</math> | |||
| If ''V'' is a potential function coming from a continuous mass distribution ''ρ''('''r'''), then ''ρ'' can be recovered using the ], {{math|Δ}}: | |||
| :<math>V(r) = \frac {2}{3} \pi G \sigma (r^2-3R^2),\qquad r\leq R,</math> | |||
| <math display="block">\rho(\mathbf{x}) = \frac{1}{4\pi G}\Delta V(\mathbf{x}).</math> | |||
| This holds pointwise whenever ''ρ'' is continuous and is zero outside of a bounded set. In general, the mass measure ''dm'' can be recovered in the same way if the Laplace operator is taken in the sense of ]s. As a consequence, the gravitational potential satisfies ]. See also ] and ]. | |||
| The integral may be expressed in terms of known transcendental functions for all ellipsoidal shapes, including the symmetrical and degenerate ones.<ref>{{cite book|title=The Theory of the Potential|first1=W.D. |last1=MacMillan|year=1958|publisher=Dover Press}}</ref> These include the sphere, where the three semi axes are equal; the oblate (see ]) and prolate spheroids, where two semi axes are equal; the degenerate ones where one semi axes is infinite (the elliptical and circular cylinder) and the unbounded sheet where two semi axes are infinite. All these shapes are widely used in the applications of the gravitational potential integral (apart from the constant ''G'', with 𝜌 being a constant charge density) to electromagnetism. | |||
| which smoothly connects to the potential function for the outside of the sphere (see the figure at the top). | |||
| ==Spherical symmetry== | |||
| A spherically symmetric mass distribution behaves to an observer completely outside the distribution as though all of the mass was concentrated at the center, and thus effectively as a ], by the ]. On the surface of the earth, the acceleration is given by so-called ] ''g'', approximately 9.8 m/s<sup>2</sup>, although this value varies slightly with latitude and altitude. The magnitude of the acceleration is a little larger at the poles than at the equator because Earth is an ]. | |||
| Within a spherically symmetric mass distribution, it is possible to solve ]. Within a uniform spherical body of radius ''R'', density ρ, and mass ''m'', the gravitational force ''g'' inside the sphere varies linearly with distance ''r'' from the center, giving the gravitational potential inside the sphere, which is<ref>{{cite book |title=A Student's Guide to Geophysical Equations |first1=William Lowrie |last1=Lowrie |publisher=Cambridge University Press |year=2011 |isbn=978-1-139-49924-8 |page=69 |url=https://books.google.com/books?id=HPE1C9vtWZ0C}} </ref><ref>{{cite book |title=An Introduction to Planetary Atmospheres |edition=illustrated |first1=Agustin |last1=Sanchez-Lavega |publisher=CRC Press |year=2011 |isbn=978-1-4200-6735-4 |page=19 |url=https://books.google.com/books?id=lCXYQ4phwbwC}} </ref> | |||
| <math display="block">V(r) = \frac {2}{3} \pi G \rho \left = \frac{Gm}{2R^3} \left, \qquad r \leq R,</math> | |||
| which differentiably connects to the potential function for the outside of the sphere (see the figure at the top). | |||
| ==General relativity== | ==General relativity== | ||
| {{see also|Gravitational acceleration#General relativity|Gravitational field#General relativity}} | |||
| In ], the gravitational potential is replaced by the ]. | |||
| In ], the gravitational potential is replaced by the ]. When the gravitational field is weak and the sources are moving very slowly compared to light-speed, general relativity reduces to Newtonian gravity, and the metric tensor can be expanded in terms of the gravitational potential.<ref name="Newtonian or gravitoelectric potential">{{citation|last1=Grøn|first1=Øyvind|last2=Hervik|first2=Sigbjorn|title=Einstein's General Theory of Relativity: With Modern Applications in Cosmology|url=https://books.google.com/books?id=IyJhCHAryuUC&pg=PA201|year=2007 |publisher=Springer Science & Business Media|isbn=978-0-387-69200-5|page=201}}</ref> | |||
| ==Gravitational potential expanded in series of Legendre polynomials== | |||
| The potential at a point '''x''' is given by | |||
| ==Multipole expansion== | |||
| :<math>V(\mathbf{x}) = - \int_{\mathbb{R}^3} \frac{G}{|\mathbf{x}-\mathbf{r}|}\ dm(\mathbf{r}).</math> | |||
| {{main|Spherical multipole moments|Multipole expansion}} | |||
| The potential at a point {{math|'''x'''}} is given by | |||
| <math display="block">V(\mathbf{x}) = - \int_{\R^3} \frac{G}{|\mathbf{x}-\mathbf{r}|}\ dm(\mathbf{r}).</math> | |||
| ] | |||
| The potential can be expanded in a series of ]. '''x''' is a vector from the center of mass to the point (i.e. "point '''x'''") at which the potential is being computed. '''r''' is a vector from the center of mass to the differential element of mass. The vector difference, '''x''' - '''r''', thus emanates from the differential element of mass to the "point '''x'''" as can be seen in the vector diagram to the right where the "point '''x'''" is denoted as '''px'''. The denominator in the integral is expressed as the square root of the square to give | |||
| The potential can be expanded in a series of ]. Represent the points '''x''' and '''r''' as ]s relative to the center of mass. The denominator in the integral is expressed as the square root of the square to give | |||
| ] | |||
| <math display="block">\begin{align} | |||
| V(\mathbf{x}) &= - \int_{\ |
V(\mathbf{x}) &= - \int_{\R^3} \frac{G}{ \sqrt{|\mathbf{x}|^2 -2 \mathbf{x} \cdot \mathbf{r} + |\mathbf{r}|^2}}\,dm(\mathbf{r})\\ | ||
| &=- \frac{1}{|\mathbf{x}|}\int_{\R^3} \frac{G} \sqrt{1 -2 \frac{r}{|\mathbf{x}|} \cos \theta + \left( \frac{r}{|\mathbf{x}|} \right)^2}\,dm(\mathbf{r}) | |||
| \end{align}</math> | \end{align}</math> | ||
| where in the last integral, r = |'''r''' |
where, in the last integral, {{math|1=''r'' = {{abs|'''r'''}}}} and {{mvar|θ}} is the angle between '''x''' and '''r'''. | ||
| (See "mathematical form".) The integrand can be expanded as a ] in {{math|1=''Z'' = ''r''/{{abs|'''x'''}}}}, by explicit calculation of the coefficients. A less laborious way of achieving the same result is by using the generalized ].<ref name="AEM">{{cite book |first=C. R. Jr. |last=Wylie |date=1960 |title=Advanced Engineering Mathematics |url=https://archive.org/details/advancedengineer00wyli |url-access=registration |location=New York |publisher=] |edition=2nd |page=454 }}</ref> The resulting series is the ] for the Legendre polynomials: | |||
| The integrand is the ] for the Legendre polynomials:<ref name="AEM">C. R. Wylie, Jr. 1960,''Advanced Engineering Mathematics'' (McGraw-Hill Book Company)</ref> | |||
| <math display="block">\left(1- 2 X Z + Z^2 \right) ^{- \frac{1}{2}} \ = \sum_{n=0}^\infty Z^n P_n(X)</math> | |||
| valid for {{math|{{abs|''X''}} ≤ 1}} and {{math|{{abs|''Z''}} < 1}}. The coefficients ''P''<sub>''n''</sub> are the Legendre polynomials of degree ''n''. Therefore, the Taylor coefficients of the integrand are given by the Legendre polynomials in {{math|1=''X'' = cos ''θ''}}. So the potential can be expanded in a series that is convergent for positions '''x''' such that {{math|''r'' < {{abs|'''x'''}}}} for all mass elements of the system (i.e., outside a sphere, centered at the center of mass, that encloses the system): | |||
| <math display="block"> \begin{align} | |||
| V(\mathbf{x}) &= - \frac{G}{|\mathbf{x}|} \int \sum_{n=0}^\infty \left(\frac{r}{|\mathbf{x}|} \right)^n P_n(\cos \theta) \, dm(\mathbf{r})\\ | |||
| &= - \frac{G}{|\mathbf{x}|} \int \left(1 + \left(\frac{r}{|\mathbf{x}|}\right) \cos \theta + \left(\frac{r}{|\mathbf{x}|}\right)^2\frac {3 \cos^2 \theta - 1}{2} + \cdots\right)\,dm(\mathbf{r}) | |||
| \end{align}</math> | |||
| The integral <math display="inline">\int r \cos(\theta) \, dm</math> is the component of the center of mass in the {{math|'''x'''}} direction; this vanishes because the vector '''x''' emanates from the center of mass. So, bringing the integral under the sign of the summation gives | |||
| <math display="block"> V(\mathbf{x}) = - \frac{GM}{|\mathbf{x}|} - \frac{G}{|\mathbf{x}|} \int \left(\frac{r}{|\mathbf{x}|}\right)^2 \frac {3 \cos^2 \theta - 1}{2} dm(\mathbf{r}) + \cdots</math> | |||
| This shows that elongation of the body causes a lower potential in the direction of elongation, and a higher potential in perpendicular directions, compared to the potential due to a spherical mass, if we compare cases with the same distance to the center of mass. (If we compare cases with the same distance to the ''surface'', the opposite is true.) | |||
| :<math>\left(1- 2 X Z + Z^2 \right) ^{- \frac{1}{2}} \ = \sum_{n=0}^\infty Z^n P_n(X)</math> | |||
| ==Numerical values== | |||
| where the ''P''<sub>''n''</sub> are the Legendre polynomials of degree ''n''. So the potential can be expanded in a series which is convergent for at least positions '''x''' such that ''r'' < |'''x'''| for all mass elements of the system (i.e., outside a sphere, centered at the center of mass, that encloses the system): | |||
| The absolute value of gravitational potential at a number of locations with regards to the gravitation from {{Clarify|date=May 2012}} the ], the ], and the ] is given in the following table; i.e. an object at Earth's surface would need 60 MJ/kg to "leave" Earth's gravity field, another 900 MJ/kg to also leave the Sun's gravity field and more than 130 GJ/kg to leave the gravity field of the Milky Way. The potential is half the square of the ]. | |||
| :<math> \begin{align} | |||
| <!-- | |||
| V(\mathbf{x}) &= - \frac{G}{|\mathbf{x}|} \int \sum_{n=0}^\infty \left(\frac{r}{|\mathbf{x}|} \right)^n P_n(\cos \theta) \, dm(\mathbf{r})\\ | |||
| theoretically, the square of the escape velocity is the potential relatively to infinity (i.e. where the inverse distance vanishes), but what means "with respect" to the central body is unclear. | |||
| {}&= - \frac{G}{|\mathbf{x}|} \int \left(1 + \left(\frac{r}{|\mathbf{x}|}\right) \cos \theta + \left(\frac{r}{|\mathbf{x}|}\right)^2\frac {3 \cos^2 \theta - 1}{2} + \cdots\right)\,dm(\mathbf{r}) | |||
| --Incnis Mrsi | |||
| \end{align}</math> | |||
| Isn't the rows the location of the observer and the column the centre of the potential well? (I rephrased the sentence somewhat; though I am not sure if it is any clearer now) | |||
| The integral, <math>\int r\cos \theta dm</math> , is the component of the center of mass in the '''x''' direction; this vanishes because the vector '''x''' emanates from the center of mass. So, bringing the integral under the sign of the summation gives | |||
| --Gunnar Larsson | |||
| :<math> V(\mathbf{x}) = - \frac{GM}{|\mathbf{x}|} - \frac{G}{|\mathbf{x}|} \int \left(\frac{r}{|\mathbf{x}|}\right)^2 \frac {3 \cos^2 \theta - 1}{2} dm(\mathbf{r}) + \cdots</math> | |||
| --> | |||
| {| class="wikitable" | |||
| This shows that elongation of the body causes a lower potential in the direction of elongation, and a higher potential in perpendicular directions, compared to the potential due to a spherical mass. | |||
| |- | |||
| ! rowspan="2" | Location | |||
| ! colspan="3" | with respect to | |||
| |- | |||
| ! ] !! ] !! ] | |||
| |- | |||
| | Earth's surface || 60 MJ/kg || 900 MJ/kg || ≥ 130 GJ/kg | |||
| |- | |||
| | ] || 57 MJ/kg || 900 MJ/kg || ≥ 130 GJ/kg | |||
| |- | |||
| | ] (17,000 million km from Earth) || 23 J/kg || 8 MJ/kg || ≥ 130 GJ/kg | |||
| |- | |||
| | 0.1 ] from Earth || 0.4 J/kg || 140 kJ/kg || ≥ 130 GJ/kg | |||
| |} | |||
| Compare the ].<!-- BTW another original research, even worse one --> | |||
| ==See also== | ==See also== | ||
| *] | * ] | ||
| * ] (''GM'') | |||
| * ] | |||
| * ] | |||
| * ] | |||
| ==Notes== | ==Notes== | ||
| <references/> | <references /> | ||
| ==References== | ==References== | ||
| {{Refbegin|2}} | |||
| * {{cite web |url=http://www.mth.uct.ac.za/omei/gr/chap5/node4.html |title=Mass in Newtonian theory |accessdate=2009-03-25 |author=Peter Dunsby |work=Tensors and Relativity: Chapter 5 Conceptual Basis of General Relativity |publisher=Department of Mathematics and Applied Mathematics University of Cape Town |date=1996-06-15 }} | |||
| * {{Citation | last1=Vladimirov | first1=V. S. | title=Equations of mathematical physics | publisher=Marcel Dekker Inc. | location=New York | series=Translated from the Russian by Audrey Littlewood. Edited by Alan Jeffrey. Pure and Applied Mathematics | mr=0268497 | date=1971 | volume=3}}. | |||
| * {{cite web |url=http://www.eas.slu.edu/People/LZhu/teaching/eas437/gravity.ppt |title=Gravity and Earth's Density Structure |accessdate=2009-03-25 |author=Lupei Zhu Associate Professor, Ph.D. (California Institute of Technology, 1998) |publisher=Saint Louis University (Department of Earth and Atmospheric Sciences)|work=EAS-437 Earth Dynamics}} | |||
| * {{cite journal|first1=W. X. | last1=Wang | title=The potential for a homogeneous spheroid in a spheroidal coordinate system. I. At an exterior point| journal= J. Phys. A: Math. Gen. | year=1988| volume=21 | issue=22 | pages=4245–4250| doi=10.1088/0305-4470/21/22/026 |bibcode=1988JPhA...21.4245W }} | |||
| * {{cite web |url=http://surveying.wb.psu.edu/sur351/geoid/grava.htm |title=The Gravity Field of the Earth|accessdate=2009-03-25 |author=Charles D. Ghilani|work=The Physics Fact Book|publisher=Penn State Surveying Engineering Program|date=2006-11-28}} | |||
| * {{cite journal|first1=T. | last1=Milon | title= A note on the potential of a homogenous ellipsoid in ellipsoidal coordinates | journal=J. Phys. A: Math. Gen. | year=1990 |volume=23 | issue=4 | pages=581–584|doi=10.1088/0305-4470/23/4/027}} | |||
| *{{Citation | last1=Thornton | first1=Stephen T. | last2=Marion | first2=Jerry B. | title=Classical Dynamics of Particles and Systems | publisher=Brooks Cole | edition=5th | isbn=978-0-534-40896-1 | year=2003}}. | |||
| *{{cite book |title=Postprincipia: Gravitation for Physicists and Astronomers | * {{cite book |title=Postprincipia: Gravitation for Physicists and Astronomers | first = Peter|last=Rastall|publisher=]|date=1991|isbn=981-02-0778-6|pages=7ff}} | ||
| * {{cite journal| first1=John T. | last1=Conway | title = Exact solutions for the gravitational potential of a family of heterogeneous spheroids| journal=Mon. Not. R. Astron. Soc. | year=2000 | volume=316 | issue=3 | pages=555–558 | doi = 10.1046/j.1365-8711.2000.03524.x |bibcode=2000MNRAS.316..555C| doi-access=free }} | |||
| |first=Peter|last=Rastall|publisher=World Scientific|year=1991|isbn=9810207786|pages=7ff.}} | |||
| * {{cite journal| first1=H. S. |last1=Cohl | first2=J. E. |last2=Tohline | first3=A. R. P. | last3=Rau |title=Developments in determining the grativational potential using toroidal functions | journal = Astron. Nachr. | year=2000 | volume=321 | number= 5/6 | pages=363–372 | doi=10.1002/1521-3994(200012)321:5/6<363::AID-ASNA363>3.0.CO;2-X | bibcode=2000AN....321..363C}} | |||
| *{{Citation | last1=Vladimirov | first1=V. S. | title=Equations of mathematical physics | publisher=Marcel Dekker Inc. | location=New York | series=Translated from the Russian by Audrey Littlewood. Edited by Alan Jeffrey. Pure and Applied Mathematics | id={{MathSciNet | id = 0268497}} | year=1971 | volume=3}}. | |||
| * {{Citation | last1=Thornton | first1=Stephen T. | last2=Marion | first2=Jerry B. | title=Classical Dynamics of Particles and Systems | publisher=Brooks Cole | edition=5th | isbn=978-0-534-40896-1 | date=2003}}. | |||
| * {{cite web|url=http://www.eas.slu.edu/People/LZhu/teaching/eas437/gravity.ppt|title=Gravity and Earth's Density Structure|access-date=2009-03-25|first1=Lupeia|last1=Zhu|year=1988|agency=California Institute of Technology|publisher=Saint Louis University|department=Department of Earth and Atmospheric Sciences|work=EAS-437 Earth Dynamics|archive-date=2011-07-26|archive-url=https://web.archive.org/web/20110726164033/http://www.eas.slu.edu/People/LZhu/teaching/eas437/gravity.ppt|url-status=dead}} | |||
| * {{cite web|url=http://surveying.wb.psu.edu/sur351/geoid/grava.htm|title=The Gravity Field of the Earth|access-date=2009-03-25|author=Charles D. Ghilani|publisher=Penn State Surveying Engineering Program|date=2006-11-28|url-status=dead|archive-url=https://web.archive.org/web/20110718143144/http://surveying.wb.psu.edu/sur351/geoid/grava.htm|archive-date=2011-07-18}} | |||
| * {{cite journal|first1=Toshio | last1=Fukushima | title= Prolate spheroidal harmonic expansion of gravitational field | journal= Astrophys. J. | year=2014 | volume=147 | page=152 |number=6| doi=10.1088/0004-6256/147/6/152|bibcode=2014AJ....147..152F| doi-access=free }} | |||
| {{Refend}} | |||
| {{Portal bar|Physics|Mathematics|Astronomy|Stars|Spaceflight|Outer space|Solar System|Science}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | ] | ||
| ] | |||
| ] | |||
Latest revision as of 13:05, 28 September 2024
Fundamental study of potential theory "Gravity potential" redirects here. For Earth's gravity potential, see Geopotential. For the field of gravity potentials, see Gravitational field.In classical mechanics, the gravitational potential is a scalar potential associating with each point in space the work (energy transferred) per unit mass that would be needed to move an object to that point from a fixed reference point in the conservative gravitational field. It is analogous to the electric potential with mass playing the role of charge. The reference point, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance. Their similarity is correlated with both associated fields having conservative forces.
Mathematically, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies.
Potential energy
Main article: Gravitational potential energyThe gravitational potential (V) at a location is the gravitational potential energy (U) at that location per unit mass:
where m is the mass of the object. Potential energy is equal (in magnitude, but negative) to the work done by the gravitational field moving a body to its given position in space from infinity. If the body has a mass of 1 kilogram, then the potential energy to be assigned to that body is equal to the gravitational potential. So the potential can be interpreted as the negative of the work done by the gravitational field moving a unit mass in from infinity.
In some situations, the equations can be simplified by assuming a field that is nearly independent of position. For instance, in a region close to the surface of the Earth, the gravitational acceleration, g, can be considered constant. In that case, the difference in potential energy from one height to another is, to a good approximation, linearly related to the difference in height:
Mathematical form
The gravitational potential V at a distance x from a point mass of mass M can be defined as the work W that needs to be done by an external agent to bring a unit mass in from infinity to that point:
where G is the gravitational constant, and F is the gravitational force. The product GM is the standard gravitational parameter and is often known to higher precision than G or M separately. The potential has units of energy per mass, e.g., J/kg in the MKS system. By convention, it is always negative where it is defined, and as x tends to infinity, it approaches zero.
The gravitational field, and thus the acceleration of a small body in the space around the massive object, is the negative gradient of the gravitational potential. Thus the negative of a negative gradient yields positive acceleration toward a massive object. Because the potential has no angular components, its gradient is where x is a vector of length x pointing from the point mass toward the small body and is a unit vector pointing from the point mass toward the small body. The magnitude of the acceleration therefore follows an inverse square law:
The potential associated with a mass distribution is the superposition of the potentials of point masses. If the mass distribution is a finite collection of point masses, and if the point masses are located at the points x1, ..., xn and have masses m1, ..., mn, then the potential of the distribution at the point x is
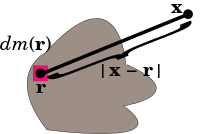
If the mass distribution is given as a mass measure dm on three-dimensional Euclidean space R, then the potential is the convolution of −G/|r| with dm. In good cases this equals the integral where |x − r| is the distance between the points x and r. If there is a function ρ(r) representing the density of the distribution at r, so that dm(r) = ρ(r) dv(r), where dv(r) is the Euclidean volume element, then the gravitational potential is the volume integral
If V is a potential function coming from a continuous mass distribution ρ(r), then ρ can be recovered using the Laplace operator, Δ: This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure dm can be recovered in the same way if the Laplace operator is taken in the sense of distributions. As a consequence, the gravitational potential satisfies Poisson's equation. See also Green's function for the three-variable Laplace equation and Newtonian potential.
The integral may be expressed in terms of known transcendental functions for all ellipsoidal shapes, including the symmetrical and degenerate ones. These include the sphere, where the three semi axes are equal; the oblate (see reference ellipsoid) and prolate spheroids, where two semi axes are equal; the degenerate ones where one semi axes is infinite (the elliptical and circular cylinder) and the unbounded sheet where two semi axes are infinite. All these shapes are widely used in the applications of the gravitational potential integral (apart from the constant G, with 𝜌 being a constant charge density) to electromagnetism.
Spherical symmetry
A spherically symmetric mass distribution behaves to an observer completely outside the distribution as though all of the mass was concentrated at the center, and thus effectively as a point mass, by the shell theorem. On the surface of the earth, the acceleration is given by so-called standard gravity g, approximately 9.8 m/s, although this value varies slightly with latitude and altitude. The magnitude of the acceleration is a little larger at the poles than at the equator because Earth is an oblate spheroid.
Within a spherically symmetric mass distribution, it is possible to solve Poisson's equation in spherical coordinates. Within a uniform spherical body of radius R, density ρ, and mass m, the gravitational force g inside the sphere varies linearly with distance r from the center, giving the gravitational potential inside the sphere, which is which differentiably connects to the potential function for the outside of the sphere (see the figure at the top).
General relativity
See also: Gravitational acceleration § General relativity, and Gravitational field § General relativityIn general relativity, the gravitational potential is replaced by the metric tensor. When the gravitational field is weak and the sources are moving very slowly compared to light-speed, general relativity reduces to Newtonian gravity, and the metric tensor can be expanded in terms of the gravitational potential.
Multipole expansion
Main articles: Spherical multipole moments and Multipole expansionThe potential at a point x is given by

The potential can be expanded in a series of Legendre polynomials. Represent the points x and r as position vectors relative to the center of mass. The denominator in the integral is expressed as the square root of the square to give where, in the last integral, r = |r| and θ is the angle between x and r.
(See "mathematical form".) The integrand can be expanded as a Taylor series in Z = r/|x|, by explicit calculation of the coefficients. A less laborious way of achieving the same result is by using the generalized binomial theorem. The resulting series is the generating function for the Legendre polynomials: valid for |X| ≤ 1 and |Z| < 1. The coefficients Pn are the Legendre polynomials of degree n. Therefore, the Taylor coefficients of the integrand are given by the Legendre polynomials in X = cos θ. So the potential can be expanded in a series that is convergent for positions x such that r < |x| for all mass elements of the system (i.e., outside a sphere, centered at the center of mass, that encloses the system): The integral is the component of the center of mass in the x direction; this vanishes because the vector x emanates from the center of mass. So, bringing the integral under the sign of the summation gives
This shows that elongation of the body causes a lower potential in the direction of elongation, and a higher potential in perpendicular directions, compared to the potential due to a spherical mass, if we compare cases with the same distance to the center of mass. (If we compare cases with the same distance to the surface, the opposite is true.)
Numerical values
The absolute value of gravitational potential at a number of locations with regards to the gravitation from the Earth, the Sun, and the Milky Way is given in the following table; i.e. an object at Earth's surface would need 60 MJ/kg to "leave" Earth's gravity field, another 900 MJ/kg to also leave the Sun's gravity field and more than 130 GJ/kg to leave the gravity field of the Milky Way. The potential is half the square of the escape velocity.
| Location | with respect to | ||
|---|---|---|---|
| Earth | Sun | Milky Way | |
| Earth's surface | 60 MJ/kg | 900 MJ/kg | ≥ 130 GJ/kg |
| LEO | 57 MJ/kg | 900 MJ/kg | ≥ 130 GJ/kg |
| Voyager 1 (17,000 million km from Earth) | 23 J/kg | 8 MJ/kg | ≥ 130 GJ/kg |
| 0.1 light-year from Earth | 0.4 J/kg | 140 kJ/kg | ≥ 130 GJ/kg |
Compare the gravity at these locations.
See also
- Applications of Legendre polynomials in physics
- Standard gravitational parameter (GM)
- Geoid
- Geopotential
- Geopotential model
Notes
- Solivérez, C.E. (2016). Electrostatics and magnetostatics of polarized ellipsoidal bodies: the depolarization tensor method (1st English ed.). Free Scientific Information. ISBN 978-987-28304-0-3.
- Marion, J.B.; Thornton, S.T. (1995). Classical Dynamics of particles and systems (4th ed.). Harcourt Brace & Company. p. 192. ISBN 0-03-097302-3.
- Arfken, George B.; Weber, Hans J. (2005). Mathematical Methods For Physicists International Student Edition (6th ed.). Academic Press. p. 72. ISBN 978-0-08-047069-6.
- Sang, David; Jones, Graham; Chadha, Gurinder; Woodside, Richard; Stark, Will; Gill, Aidan (2014). Cambridge International AS and A Level Physics Coursebook (illustrated ed.). Cambridge University Press. p. 276. ISBN 978-1-107-69769-0.
- Muncaster, Roger (1993). A-level Physics (illustrated ed.). Nelson Thornes. p. 106. ISBN 978-0-7487-1584-8.
- MacMillan, W.D. (1958). The Theory of the Potential. Dover Press.
- Lowrie, William Lowrie (2011). A Student's Guide to Geophysical Equations. Cambridge University Press. p. 69. ISBN 978-1-139-49924-8. Extract of page 68
- Sanchez-Lavega, Agustin (2011). An Introduction to Planetary Atmospheres (illustrated ed.). CRC Press. p. 19. ISBN 978-1-4200-6735-4. Extract of page 19
- Grøn, Øyvind; Hervik, Sigbjorn (2007), Einstein's General Theory of Relativity: With Modern Applications in Cosmology, Springer Science & Business Media, p. 201, ISBN 978-0-387-69200-5
- Wylie, C. R. Jr. (1960). Advanced Engineering Mathematics (2nd ed.). New York: McGraw-Hill. p. 454 .
References
- Vladimirov, V. S. (1971), Equations of mathematical physics, Translated from the Russian by Audrey Littlewood. Edited by Alan Jeffrey. Pure and Applied Mathematics, vol. 3, New York: Marcel Dekker Inc., MR 0268497.
- Wang, W. X. (1988). "The potential for a homogeneous spheroid in a spheroidal coordinate system. I. At an exterior point". J. Phys. A: Math. Gen. 21 (22): 4245–4250. Bibcode:1988JPhA...21.4245W. doi:10.1088/0305-4470/21/22/026.
- Milon, T. (1990). "A note on the potential of a homogenous ellipsoid in ellipsoidal coordinates". J. Phys. A: Math. Gen. 23 (4): 581–584. doi:10.1088/0305-4470/23/4/027.
- Rastall, Peter (1991). Postprincipia: Gravitation for Physicists and Astronomers. World Scientific. pp. 7ff. ISBN 981-02-0778-6.
- Conway, John T. (2000). "Exact solutions for the gravitational potential of a family of heterogeneous spheroids". Mon. Not. R. Astron. Soc. 316 (3): 555–558. Bibcode:2000MNRAS.316..555C. doi:10.1046/j.1365-8711.2000.03524.x.
- Cohl, H. S.; Tohline, J. E.; Rau, A. R. P. (2000). "Developments in determining the grativational potential using toroidal functions". Astron. Nachr. 321 (5/6): 363–372. Bibcode:2000AN....321..363C. doi:10.1002/1521-3994(200012)321:5/6<363::AID-ASNA363>3.0.CO;2-X.
- Thornton, Stephen T.; Marion, Jerry B. (2003), Classical Dynamics of Particles and Systems (5th ed.), Brooks Cole, ISBN 978-0-534-40896-1.
- Zhu, Lupeia (1988). "Gravity and Earth's Density Structure". Department of Earth and Atmospheric Sciences. EAS-437 Earth Dynamics. Saint Louis University. California Institute of Technology. Archived from the original on 2011-07-26. Retrieved 2009-03-25.
- Charles D. Ghilani (2006-11-28). "The Gravity Field of the Earth". Penn State Surveying Engineering Program. Archived from the original on 2011-07-18. Retrieved 2009-03-25.
- Fukushima, Toshio (2014). "Prolate spheroidal harmonic expansion of gravitational field". Astrophys. J. 147 (6): 152. Bibcode:2014AJ....147..152F. doi:10.1088/0004-6256/147/6/152.


 where G is the
where G is the  where x is a vector of length x pointing from the point mass toward the small body and
where x is a vector of length x pointing from the point mass toward the small body and  is a unit vector pointing from the point mass toward the small body. The magnitude of the acceleration therefore follows an
is a unit vector pointing from the point mass toward the small body. The magnitude of the acceleration therefore follows an 

 where |x − r| is the
where |x − r| is the 
 This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure dm can be recovered in the same way if the Laplace operator is taken in the sense of
This holds pointwise whenever ρ is continuous and is zero outside of a bounded set. In general, the mass measure dm can be recovered in the same way if the Laplace operator is taken in the sense of  which differentiably connects to the potential function for the outside of the sphere (see the figure at the top).
which differentiably connects to the potential function for the outside of the sphere (see the figure at the top).

 where, in the last integral, r = |r| and θ is the angle between x and r.
where, in the last integral, r = |r| and θ is the angle between x and r.
 valid for |X| ≤ 1 and |Z| < 1. The coefficients Pn are the Legendre polynomials of degree n. Therefore, the Taylor coefficients of the integrand are given by the Legendre polynomials in X = cos θ. So the potential can be expanded in a series that is convergent for positions x such that r < |x| for all mass elements of the system (i.e., outside a sphere, centered at the center of mass, that encloses the system):
valid for |X| ≤ 1 and |Z| < 1. The coefficients Pn are the Legendre polynomials of degree n. Therefore, the Taylor coefficients of the integrand are given by the Legendre polynomials in X = cos θ. So the potential can be expanded in a series that is convergent for positions x such that r < |x| for all mass elements of the system (i.e., outside a sphere, centered at the center of mass, that encloses the system):
 The integral
The integral  is the component of the center of mass in the x direction; this vanishes because the vector x emanates from the center of mass. So, bringing the integral under the sign of the summation gives
is the component of the center of mass in the x direction; this vanishes because the vector x emanates from the center of mass. So, bringing the integral under the sign of the summation gives
