| Revision as of 18:10, 1 April 2010 edit64.206.30.2 (talk) →Planck's law of black-body radiation← Previous edit | Latest revision as of 03:22, 29 November 2024 edit undoReaper1945 (talk | contribs)Extended confirmed users, Pending changes reviewers7,149 edits Newton discussed the notion of black bodies his Opticks book.Tags: Visual edit Mobile edit Mobile web edit | ||
| Line 1: | Line 1: | ||
| {{Short description|Idealized physical body that absorbs all incident electromagnetic radiation}} | |||
| ] | |||
| {{redirect-distinguish|Black bodies|Black Bodies (film)}} | |||
| ] utilized as a ] standard.]] | |||
| {{Use dmy dates |date=October 2020}} | |||
| ] and its ].]] | |||
| A '''black body''' or '''blackbody''' is an idealized ] that ] all incident ], regardless of frequency or ]. The radiation emitted by a black body in thermal equilibrium with its environment is called '']''. The name "black body" is given because it absorbs all colors of light. In contrast, a '''white body''' is one with a "rough surface that reflects all incident rays completely and uniformly in all directions."<ref>{{harvnb|Planck|1914|pages=9–10}}</ref> | |||
| ]) of black-body radiation depends on the temperature of the black body; the ] of such colors, shown here in ], is known as the ].]] | |||
| A black body in ] (that is, at a constant temperature) emits electromagnetic black-body radiation. The radiation is emitted according to ], meaning that it has a ] that is determined by the ] alone (see figure at right), not by the body's shape or composition. | |||
| In ], a '''black body''' is an idealized ] that absorbs all ] that falls on it. No electromagnetic radiation passes through it and none is ]. Because no light (visible electromagnetic radiation) is reflected or transmitted, the object appears black when it is cold. However, a black body emits a temperature-dependent ] of light. This ] from a black body is termed '''black-body radiation'''.<ref group="nb">When used as a ], the term is typically hyphenated, as in "black-body radiation", or combined into one word, as in "blackbody radiation". The hyphenated and one-word forms should not generally be used as nouns.</ref> | |||
| An ideal black body in thermal equilibrium has two main properties:<ref name=Massoud/> | |||
| #It is an ideal emitter: at every frequency, it emits as much or more thermal radiative energy as any other body at the same temperature. | |||
| #It is a diffuse emitter: measured per unit area perpendicular to the direction, the energy is radiated ], independent of direction. | |||
| Real materials emit energy at a fraction—called the ]—of black-body energy levels. By definition, a black body in thermal equilibrium has an emissivity {{nowrap|''ε'' {{=}} 1}}. A source with a lower emissivity, independent of frequency, is often referred to as a gray body.<ref name=emissivity/><ref name=gray_body/> | |||
| Constructing black bodies with an emissivity as close to 1 as possible remains a topic of current interest.<ref name=Chun/> | |||
| In ], the radiation from ]s and ]s is sometimes characterized in terms of an ], the temperature of a black body that would emit the same total flux of electromagnetic energy. | |||
| == Definition == | |||
| ] introduced the notion of a black body in his 1704 book '']'', with query 6 of the book stating:<ref>{{Cite book |last=Bochner |first=Salomon |url=https://books.google.com/books?id=naH_AwAAQBAJ&pg=PA221 |title=Role of Mathematics in the Rise of Science |date=1981 |publisher=Princeton Univ. Pr |isbn=978-0-691-08028-4 |edition= |location=Princeton, NJ |pages=221, 347 |language=en}}</ref><ref>{{Cite book |last=Rowlands |first=Peter |url=https://books.google.com/books?id=u0NBDwAAQBAJ&pg=PA69 |title=Newton - Innovation And Controversy |publisher=] |year=2017 |isbn=9781786344045 |pages=69 |language=en}}</ref>{{blockquote|Do not black Bodies conceive heat more easily from Light than those of other Colours do, by reason that the Light falling on them is not reflected outwards, but enters into the Bodies, and is often reflected and refracted within them, until it be stifled and lost?}}The idea of a black body originally was introduced by ] in 1860 as follows: | |||
| {{blockquote|...the supposition that bodies can be imagined which, for infinitely small thicknesses, completely absorb all incident rays, and neither reflect nor transmit any. I shall call such bodies ''perfectly black'', or, more briefly, ''black bodies''.<ref name=Kirchhoff/>}} | |||
| A more modern definition drops the reference to "infinitely small thicknesses":<ref name=infinitesimal/> | |||
| {{blockquote|An ideal body is now defined, called a ''blackbody''. A ''blackbody'' allows ''all'' incident radiation to pass into it (no reflected energy) and internally absorbs ''all'' the incident radiation (no energy transmitted through the body). This is true for radiation of all wavelengths and for all angles of incidence. Hence the blackbody is ''a perfect absorber for all incident radiation.''<ref name=Siegel/>}} | |||
| == Idealizations == | |||
| This section describes some concepts developed in connection with black bodies. | |||
| ] | |||
| === Cavity with a hole === | |||
| A widely used model of a black surface is a small hole in a cavity with walls that are opaque to radiation.<ref name=Siegel/> Radiation incident on the hole will pass into the cavity, and is very unlikely to be re-emitted if the cavity is large. Lack of any re-emission, means that the hole is behaving like a perfect black surface. The hole is not quite a perfect black surface—in particular, if the wavelength of the incident radiation is greater than the diameter of the hole, part will be reflected. Similarly, even in perfect thermal equilibrium, the radiation inside a finite-sized cavity will not have an ideal Planck spectrum for wavelengths comparable to or larger than the size of the cavity.<ref name=Zee/> | |||
| Suppose the cavity is held at a fixed temperature ''T'' and the radiation trapped inside the enclosure is at ] with the enclosure. The hole in the enclosure will allow some radiation to escape. If the hole is small, radiation passing in and out of the hole has negligible effect upon the equilibrium of the radiation inside the cavity. This escaping radiation will approximate ] that exhibits a distribution in energy characteristic of the temperature ''T'' and does not depend upon the properties of the cavity or the hole, at least for wavelengths smaller than the size of the hole.<ref name=Zee/> See the figure in the Introduction for the ] as a function of the ] of the radiation, which is related to the energy of the radiation by the equation ''E'' = ''hf'', with ''E'' = energy, ''h'' = ], ''f'' = frequency. | |||
| At any given time the radiation in the cavity may not be in thermal equilibrium, but ] states that if left undisturbed it will eventually reach equilibrium,<ref name="Adkins"/> although the time it takes to do so may be very long.<ref name=Batrouni/> Typically, equilibrium is reached by continual absorption and emission of radiation by material in the cavity or its walls.<ref name=Landsberg/><ref name="Planck 1914 44">{{harvnb|Planck|1914|page=44, §52}}</ref><ref>{{harvnb|Loudon|2000}}, Chapter 1</ref><ref>{{harvnb|Mandel|Wolf|1995}}, Chapter 13</ref> Radiation entering the cavity will be "]" by this mechanism: the energy will be redistributed until the ensemble of photons achieves a ]. The time taken for thermalization is much faster with condensed matter present than with rarefied matter such as a dilute gas. At temperatures below billions of Kelvin, direct ]<ref name=Karplus>Robert Karplus* and Maurice Neuman, "The Scattering of Light by Light", Phys. Rev. 83, 776–784 (1951)</ref> are usually negligible compared to interactions with matter.<ref name=Bergmann/> Photons are an example of an interacting ] gas,<ref name=boson/> and as described by the ],<ref name=Tolman/> under very general conditions any interacting boson gas will approach thermal equilibrium. | |||
| === Transmission, absorption, and reflection === | |||
| A body's behavior with regard to thermal radiation is characterized by its transmission ''τ'', absorption ''α'', and reflection ''ρ''. | |||
| The boundary of a body forms an interface with its surroundings, and this interface may be rough or smooth. A nonreflecting interface separating regions with different refractive indices must be rough, because the laws of reflection and refraction governed by the ] for a smooth interface require a reflected ray when the refractive indices of the material and its surroundings differ.<ref name=Tipler/> A few idealized types of behavior are given particular names: | |||
| At room temperature, black bodies emit mostly ] wavelengths, but as the temperature increases past a few hundred degrees ], black bodies start to emit visible wavelengths, appearing red, orange, yellow, white, and blue with increasing temperature. By the time an object is white, it is emitting substantial ] radiation. | |||
| An '']'' is one that transmits none of the radiation that reaches it, although some may be reflected.<ref name=Kaviany/><ref name=Venkanna/> That is, ''τ'' = 0 and ''α'' + ''ρ'' = 1. | |||
| The term "black body" was introduced by ] in 1860. | |||
| A '']'' is one that transmits all the radiation that reaches it. That is, ''τ'' = 1 and ''α'' = ''ρ'' = 0. | |||
| Black-body emission gives insight into the thermal equilibrium state of a continuous field. In classical physics, each different ] in thermal equilibrium should have the ]. This approach led to the paradox known as the ], that there would be an infinite amount of energy in any continuous field. Black bodies could test the properties of thermal equilibrium because they emit radiation which is distributed thermally. Studying the laws of the black body historically led to ]. | |||
| A '''''grey body''''' is one where ''α'', ''ρ'' and ''τ'' are constant for all wavelengths; this term also is used to mean a body for which ''α'' is temperature- and wavelength-independent. | |||
| ==Explanation== | |||
| ] | |||
| A ''white body'' is one for which all incident radiation is reflected uniformly in all directions: ''τ'' = 0, ''α'' = 0, and ''ρ'' = 1. | |||
| Black-body radiation is light in thermal equilibrium with a black body, light radiation with a given temperature. It is the reference ] state of light. Experimentally, it is established as the steady state equilibrium radiation in a rigid-walled cavity that contains a black body. There are no strictly exact black bodies in nature, but graphite is a good approximation, and a closed box with graphite walls at a steady state gives a good approximation to ideal black body radiation<ref>G. Kirchhoff (1896). On the relation between the Radiating and Absorbing Powers of different Bodies for Light and Heat, translated by F. Guthrie in ''Phil. Mag.'' Series 4, volume 20, number 130, pages 1-21, original in Poggendorff's ''Annalen'', vol. 109, pages 275 ''et seq.''</ref><ref>M. Planck (1914). ''The theory of heat radiation'', second edition, translated by M. Masius, Blackiston's Son & Co, Philadelphia.</ref><ref>{{cite journal|doi=10.1109/TPS.2003.820958|title=On the validity of Kirchhoff's law of thermal emission|year=2003|last1=Robitaille|first1=P.|journal=IEEE Transactions on Plasma Science|volume=31|pages=1263}}</ref>. A cavity that does not contain any black material body does not sustain black body radiation at equilibrium; this fact was found experimentally by Kirchhoff but its physical significance was understood neither by Kirchhoff nor by Planck. | |||
| For a black body, ''τ'' = 0, ''α'' = 1, and ''ρ'' = 0. Planck offers a theoretical model for perfectly black bodies, which he noted do not exist in nature: besides their opaque interior, they have interfaces that are perfectly transmitting and non-reflective.<ref>{{harvnb|Planck|1914|page=10}}</ref> | |||
| Because light is the oscillation of a continuous ], the study of black-body radiation reveals how continuous fields can have a temperature, something which contradicts ]. Because the thermal state of light was so confusing before the advent of ], the ] arguments that light has a thermal equilibrium state were made very carefully. | |||
| === Kirchhoff's perfect black bodies === | |||
| An object at some fixed temperature ''T'', like an oven, is observed to glow. The '']'' is the name given to the point at which all solids glow a dim red (about 798 K).<ref>{{cite journal | |||
| Kirchhoff in 1860 introduced the theoretical concept of a perfect black body with a completely absorbing surface layer of infinitely small thickness, but Planck noted some severe restrictions upon this idea. Planck noted three requirements upon a black body: the body must (i) allow radiation to enter but not reflect; (ii) possess a minimum thickness adequate to absorb the incident radiation and prevent its re-emission; (iii) satisfy severe limitations upon ] to prevent radiation from entering and bouncing back out. As a consequence, Kirchhoff's perfect black bodies that absorb all the radiation that falls on them cannot be realized in an infinitely thin surface layer, and impose conditions upon scattering of the light within the black body that are difficult to satisfy.<ref>{{harvnb|Planck|1914|pages=9–10, §10}}</ref><ref name="Kirchhoff 1860c">{{harvnb|Kirchhoff|1860c}}</ref> | |||
| |journal = The Academy | |||
| |title = Science: Draper's Memoirs | |||
| |volume = XIV | |||
| |issue = 338 | |||
| |publisher = London: Robert Scott Walker | |||
| |date = Oct. 26, 1878 | |||
| |page = 408 | |||
| |url = http://books.google.com/books?id=hZINAAAAQAAJ&pg=PA408&dq=draper+point+red+1847&lr=&as_brr=0&ei=6sxtSpnpLoLglATlh4RW | |||
| }}</ref><ref>{{cite book | |||
| |title = Radiation heat transfer: a statistical approach | |||
| |author = J. R. Mahan | |||
| |edition = 3rd | |||
| |publisher = Wiley-IEEE | |||
| |year = 2002 | |||
| |isbn = 9780471212706 | |||
| |page = 58 | |||
| |url = http://books.google.com/books?id=y9zUEzA7iN0C&pg=PA58&dq=draper-point+red&lr=&as_drrb_is=q&as_minm_is=0&as_miny_is=&as_maxm_is=0&as_maxy_is=&as_brr=3&ei=H8ttSo_2LImMkQTwvuxO | |||
| }}</ref> | |||
| At 1000 K, an oven looks red; at 6000 K, it looks white. No matter how the oven is constructed, so long as the oven is not too shiny, the color of the light only depends on the temperature. Since color is the directly visible measure of the ], this observation means that light at different temperatures has a different distribution of energy among the different wavelengths. The amount of energy E per unit volume in wavelength ''λ'' at temperature ''T'' is called the ''black-body curve''. Detailed experiments revealed that the black-body curve only depends on the temperature, not on the emitting body. This suggests that light does in fact come to thermal equilibrium just like anything else, that the concept of ''light at temperature T'' makes sense. | |||
| == Realizations == | |||
| ] lava flow can be estimated by observing its color. The result agrees well with measured temperatures of lava flows at about 1000 to 1200 °C.]] Two things that are at the same temperature stay in equilibrium, so a body at temperature ''T'' surrounded by a cloud of light at temperature ''T'' on average will emit as much light into the cloud as it absorbs, following Prevost's exchange principle, which refers to ]. The principle of ] says that there are no strange correlations between the process of emission and absorption: the process of emission is not affected by the absorption, but only by the thermal state of the emitting body. This means that the total light emitted by a body at temperature ''T'', black or not, is always equal to the total light that the body would absorb were it to be surrounded by light at temperature ''T''. | |||
| A ''realization'' of a black body refers to a real world, physical embodiment. Here are a few. | |||
| === Cavity with a hole === | |||
| When the body is black, the absorption is obvious: the amount of light absorbed is all the light that hits the surface. For a black body much bigger than the wavelength, the light energy absorbed at any wavelength ''λ'' per unit time is strictly proportional to the black-body curve. This means that the black-body curve is the amount of light energy emitted by a black body, which justifies the name.<ref group="nb">There is a subtlety when the black body is small, so that its size is comparable to the wavelength of light. In this case, the absorption is modified, because a small object is not an efficient absorber of light of long wavelength. But the principle of strict equality of emission and absorption is always upheld.</ref> This is ]: the black-body emission curve is a thermal characteristic of light, which depends only on the ] of the walls of the cavity, provided strictly that the cavity contains some perfectly black material body and is in ].<ref name="Huang">{{cite book |last=Huang |first=Kerson|title=Statistical Mechanics |year=1967 |publisher=John Wiley & Sons |location=New York}}</ref> | |||
| In 1898, ] and ] published an account of their cavity radiation source.<ref>{{harvnb|Lummer|Kurlbaum|1898}}</ref> Their design has been used largely unchanged for radiation measurements to the present day. It was a hole in the wall of a platinum box, divided by diaphragms, with its interior blackened with iron oxide. It was an important ingredient for the progressively improved measurements that led to the discovery of Planck's law.<ref name=Rechenberg/><ref>{{harvnb|Kangro|1976|page=159}}</ref> A version described in 1901 had its interior blackened with a mixture of chromium, nickel, and cobalt oxides.<ref>{{harvnb|Lummer|Kurlbaum|1901}}</ref> See also ]. | |||
| === Near-black materials === | |||
| In the laboratory, black-body radiation is approximated by the radiation from a small hole entrance to a large cavity, a ], that contains a black body, and that has reached and is maintained at equilibrium. (This technique leads to the alternative term ''cavity radiation''.) Any light entering the hole would have to reflect off the walls of the cavity multiple times before it escaped, in which process it is nearly certain to be absorbed. This occurs regardless of the ] of the radiation entering (as long as it is small compared to the hole). The hole, then, is a close approximation of a theoretical black body and, if the cavity is heated, the ] of the hole's radiation (i.e., the amount of light emitted from the hole at each ]) will be continuous, strictly provided that the cavity must contain some nearly perfectly black material body and that equilibrium has been reached and is maintained, but with these provisoes, it does not further depend on the other material in the cavity (compare with ]). | |||
| There is interest in blackbody-like materials for ] and ]s for radar invisibility.<ref name=Lewis/><ref name=Quinn/> They also have application as solar energy collectors, and infrared thermal detectors. As a perfect emitter of radiation, a hot material with black body behavior would create an efficient infrared heater, particularly in space or in a vacuum where convective heating is unavailable.<ref name=Mizuno/> They are also useful in telescopes and cameras as anti-reflection surfaces to reduce stray light, and to gather information about objects in high-contrast areas (for example, observation of planets in orbit around their stars), where blackbody-like materials absorb light that comes from the wrong sources. | |||
| It has long been known that a ] coating will make a body nearly black. An improvement on lamp-black is found in manufactured ]s. Nano-porous materials can achieve ] nearly that of vacuum, in one case obtaining average reflectance of 0.045%.<ref name=Chun/><ref name=Yang/> In 2009, a team of Japanese scientists created a material called nanoblack which is close to an ideal black body, based on vertically aligned single-walled ]. This absorbs between 98% and 99% of the incoming light in the spectral range from the ultra-violet to the far-infrared regions.<ref name=Mizuno/> | |||
| Calculating the black-body curve was a major challenge in theoretical physics during the late nineteenth century. The problem was finally solved in 1901 by ] as ].<ref>{{cite journal | |||
| |last = Planck | |||
| |first = Max | |||
| |authorlink = Max_Planck | |||
| |coauthors = | |||
| |title =On the Law of Distribution of Energy in the Normal Spectrum | |||
| |journal = ] | |||
| |volume = 4 | |||
| |pages = 553 | |||
| |date = 1901 | |||
| |url = http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Planck-1901/Planck-1901.html | |||
| |format = {{dead link|date=November 2009}}}}</ref> | |||
| By making changes to ] (not to be confused with ]) consistent with ] and ], he found a mathematical formula fitting the experimental data in a satisfactory way. To find a physical interpretation for this formula, Planck had then to assume that the energy of the oscillators in the cavity was quantized (i.e., integer multiples of some quantity). ] built on this idea and proposed the quantization of electromagnetic radiation itself in 1905 to explain the ]. These theoretical advances eventually resulted in the superseding of classical electromagnetism by ]. Today, these quanta are called ]s and the black-body cavity may be thought of as containing a ]. In addition, it led to the development of quantum probability distributions, called ] and ], each applicable to a different class of particle, which are used in quantum mechanics instead of the classical distributions. ''See also'' ] ''and'' ]. | |||
| Other examples of nearly perfect black materials are ], prepared by chemically etching a ]–] ],<ref name=Brown/> ] (like ]) and flower carbon nanostructures;<ref>{{Cite journal |doi = 10.1021/acsanm.9b01950|title = Dandelion-Like Carbon Nanotubes for Near-Perfect Black Surfaces|year = 2019|last1 = Ghai|first1 = Viney|last2 = Singh|first2 = Harpreet|last3 = Agnihotri|first3 = Prabhat K.|journal = ACS Applied Nano Materials|volume = 2|issue = 12|pages = 7951–7956| s2cid=213017898 }}</ref> all absorb 99.9% of light or more. | |||
| The wavelength at which the radiation is strongest is given by ], and the overall power emitted per unit area is given by the ]. So, as temperature increases, the glow color changes from red to yellow to white to blue. Even as the peak wavelength moves into the ultra-violet, enough radiation continues to be emitted in the blue wavelengths that the body will continue to appear blue. It will never become invisible—indeed, the radiation of visible light increases ] with temperature.<ref name="Landau">{{cite book |last=Landau |first=L. D.|coauthors=E. M. Lifshitz|title=Statistical Physics |edition=3rd Edition Part 1 |year=1996|publisher=Butterworth-Heinemann |location=Oxford}}</ref> | |||
| === Stars and planets <span class="anchor" id="stars_and_planets_anchor"></span> === | |||
| The ] or observed intensity is not a function of direction. Therefore a black body is a perfect ] radiator. | |||
| {{For| more about the UBV color index|Photometric system}} | |||
| ] (a ]), the Sun (a ]), ] (a ]), ] (a blue star), and ].]] | |||
| A star or planet often is modeled as a black body, and electromagnetic radiation emitted from these bodies as ]. The figure shows a highly schematic cross-section to illustrate the idea. The ] of the star, where the emitted light is generated, is idealized as a layer within which the photons of light interact with the material in the photosphere and achieve a common temperature ''T'' that is maintained over a long period of time. Some photons escape and are emitted into space, but the energy they carry away is replaced by energy from within the star, so that the temperature of the photosphere is nearly steady. Changes in the core lead to changes in the supply of energy to the photosphere, but such changes are slow on the time scale of interest here. Assuming these circumstances can be realized, the outer layer of the star is somewhat analogous to the example of an enclosure with a small hole in it, with the hole replaced by the limited transmission into space at the outside of the photosphere. With all these assumptions in place, the star emits black-body radiation at the temperature of the photosphere.<ref name="Green" /> | |||
| Real objects never behave as full-ideal black bodies, and instead the emitted radiation at a given frequency is a fraction of what the ideal emission would be. The ] of a material specifies how well a real body radiates energy as compared with a black body. This emissivity depends on factors such as temperature, emission angle, and wavelength. However, it is typical in engineering to assume that a surface's spectral emissivity and absorptivity do not depend on wavelength, so that the emissivity is a constant. This is known as the '''grey body''' assumption. | |||
| ] contains ]s of light nearly in thermal equilibrium, and some escape into space as near-black-body radiation. ]] | |||
| ] image of the ] radiation ]. It has the most precise ] spectrum known and corresponds to a temperature of 2.725 K with an emission peak at 160.2 ].]] | |||
| Due to the rapid fall-off of emitted photons with decreasing energy, a black body at room temperature (300 K) with 1 m<sup>2</sup> of surface area emits a visible photon every thousand years or so, which is negligible for most purposes. | |||
| Using this model the ] of stars is estimated, defined as the temperature of a black body that yields the same surface flux of energy as the star. If a star were a black body, the same effective temperature would result from any region of the spectrum. For example, comparisons in the ''B'' (blue) or ''V'' (visible) range lead to the so-called ''B-V'' ], which increases the redder the star,<ref name=Kelley/> with the Sun having an index of +0.648 ± 0.006.<ref name=Gray/> Combining the ''U'' (ultraviolet) and the ''B'' indices leads to the ''U-B'' index, which becomes more negative the hotter the star and the more the UV radiation. Assuming the Sun is a type G2 V star, its ''U-B'' index is +0.12.<ref name=Golay/> The two indices for two types of most common star sequences are compared in the figure (diagram) with the effective surface temperature of the stars if they were perfect black bodies. There is a rough correlation. For example, for a given ''B-V'' index measurement, the curves of both most common sequences of star (the main sequence and the supergiants) lie below the corresponding black-body ''U-B'' index that includes the ultraviolet spectrum, showing that both groupings of star emit less ultraviolet light than a black body with the same ''B-V'' index. It is perhaps surprising that they fit a black body curve as well as they do, considering that stars have greatly different temperatures at different depths.<ref name=Aller/> For example, the ] has an effective temperature of 5780 K,<ref name=Lang/> which can be compared to the temperature of its ] (the region generating the light), which ranges from about 5000 K at its outer boundary with the ] to about 9500 K at its inner boundary with the ] approximately {{convert|500|km|abbr=on}} deep.<ref name=Bertotti/> | |||
| When dealing with non-black surfaces, the deviations from ideal black-body behavior are determined by both the geometrical structure and the chemical composition, and, provided there is a ] with a nearly black body that is present, nearly follow ]: emissivity equals absorptivity, so that an object that does not absorb all incident light will also emit less radiation than an ideal black body. | |||
| ].<ref name="UBV" />]] | |||
| In ], objects such as ]s are frequently regarded as black bodies, though this is often a poor approximation. An almost perfect black-body spectrum is exhibited by the ]. ] is the hypothetical black-body radiation emitted by ]s. | |||
| === Black holes === | |||
| ] | |||
| {{See also|Hawking radiation}} | |||
| ===Black-body simulators=== | |||
| A ] is a region of ] from which nothing escapes. Around a black hole there is a mathematically defined surface called an ] that marks the ]. It is called "black" because it absorbs all the light that hits the horizon, reflecting nothing, making it almost an ideal black body<ref name=Schutz/> (radiation with a wavelength equal to or larger than the diameter of the hole may not be absorbed, so black holes are not perfect black bodies).<ref name=Davies/> Physicists believe that to an outside observer, black holes have a non-zero temperature and emit ], radiation with a nearly perfect black-body spectrum, ultimately ].<ref name=Wald/> The mechanism for this emission is related to ] in which a ] of particles is separated by the gravity of the hole, one member being sucked into the hole, and the other being emitted.<ref name=Carr/> The energy distribution of emission is described by ] with a temperature ''T'': | |||
| Although a black body is a theoretical object (i.e. emissivity ''e'' = 1.0), common applications define a source of infrared radiation as a black body when the object approaches an emissivity of 1.0, (typically ''e'' = 0.99 or better). A source of infrared radiation less than 0.99 is referred to as a "grey body".<ref>Electro Optical Industries, Inc. (2008) In ''BB Radiation''</ref> Applications for '''black body simulators''' typically include the testing and calibration of infrared systems and infrared sensor equipment. | |||
| :<math>T=\frac {\hbar c^3}{8\pi Gk_\text{B}M} \ ,</math> | |||
| where ''c'' is the ], ℏ is the ], ''k''<sub>B</sub> is the ], ''G'' is the ] and ''M'' is the mass of the black hole.<ref name=Frolov/> These predictions have not yet been tested either observationally or experimentally.<ref name=Wald2/> | |||
| === Cosmic microwave background radiation === | |||
| ] is an example of such a material, made from a ]-] ]. More recently, a team of Japanese scientists created a material even closer to a black body, based on vertically aligned single-walled ], which absorbs between 98% and 99% of the incoming light, in the spectral range from UV to far infrared.<ref>{{cite journal | |||
| {{See also|Big Bang|Cosmic microwave background radiation}} | |||
| |author=K. Mizuno ''et al.'' | |||
| The Big Bang theory is based upon the ], which states that on large scales the Universe is homogeneous and isotropic. According to theory, the Universe approximately a second after its formation was a near-ideal black body in thermal equilibrium at a temperature above 10<sup>10</sup> K. The temperature decreased as the Universe expanded and the matter and radiation in it cooled. The cosmic microwave background radiation observed today is "the most perfect black body ever measured in nature".<ref name=White/> It has a nearly ideal Planck spectrum at a temperature of about 2.7 K. It departs from the perfect isotropy of true black-body radiation by an observed anisotropy that varies with angle on the sky only to about one part in 100,000. | |||
| |title=A black body absorber from vertically aligned single-walled carbon nanotubes | |||
| |journal=] | |||
| |volume=106 |format=free download|pages=6044–6077 | |||
| |year=2009 | |||
| |doi=10.1073/pnas.0900155106}} | |||
| </ref> | |||
| == Radiative cooling == | |||
| ==Equations governing black bodies== | |||
| ] and ] vs ] temperature – red arrows show that ] black bodies have 501 nm peak wavelength and 63.3 MW/m<sup>2</sup>; radiant exitance]] | |||
| ===Planck's law of black-body radiation=== | |||
| {{See also|Radiative cooling|Radiosity (heat transfer)}} | |||
| {{Main|Planck's law}} | |||
| The integration of ] over all frequencies provides the total energy per unit of time per unit of surface area radiated by a black body maintained at a temperature ''T'', and is known as the ]: | |||
| Planck's law states that | |||
| :<math> |
:<math>P/A = \sigma T^4 \ , </math> | ||
| where ''σ'' is the ], {{physconst|sigma|symbol=yes|round=2|end=.}} To remain in thermal equilibrium at constant temperature ''T'', the black body must absorb or internally generate this amount of ] ''P'' over the given area ''A''. | |||
| where | |||
| :''I''(''ν'',''T'') ''dν'' is the amount of ] per unit ] per unit ] per unit ] emitted in the frequency range between ''ν'' and {{nowrap|''ν'' + ''dν''}} by a black body at temperature ''T''; | |||
| :''h'' is the ]; | |||
| :''c'' is the ] in a vacuum; | |||
| :''k'' is the ]; | |||
| :''ν'' is ] of electromagnetic radiation; and | |||
| :''T'' is the ] in ]s. | |||
| The cooling of a body due to thermal radiation is often approximated using the Stefan–Boltzmann law supplemented with a "gray body" ] {{nowrap|''ε'' ≤ 1}} ({{nowrap|1=''P''/''A'' = ''εσT''{{i sup|4}}}}). The rate of decrease of the temperature of the emitting body can be estimated from the power radiated and the body's ].<ref name=Pearson/> This approach is a simplification that ignores details of the mechanisms behind heat redistribution (which may include changing composition, ]s or restructuring of the body) that occur within the body while it cools, and assumes that at each moment in time the body is characterized by a single temperature. It also ignores other possible complications, such as changes in the emissivity with temperature,<ref name=Vollmer/><ref name=Champion/> and the role of other accompanying forms of energy emission, for example, emission of particles like neutrinos.<ref name=Shifman/> | |||
| ===Wien's displacement law=== | |||
| {{Main|Wien's displacement law}} | |||
| Wien's displacement law shows how the spectrum of black body radiation at any temperature is related to the spectrum at any other temperature. If we know the shape of the spectrum at one temperature, we can calculate the shape at any other temperature. | |||
| If a hot emitting body is assumed to follow the Stefan–Boltzmann law and its power emission ''P'' and temperature ''T'' are known, this law can be used to estimate the dimensions of the emitting object, because the total emitted power is proportional to the area of the emitting surface. In this way it was found that X-ray bursts observed by astronomers originated in neutron stars with a radius of about 10 km, rather than black holes as originally conjectured.<ref name=Lewin/> An accurate estimate of size requires some knowledge of the emissivity, particularly its spectral and angular dependence.<ref name=Mason/> | |||
| A consequence of Wien's displacement law is that the wavelength at which the intensity of the radiation produced by a black body is at a maximum, <math>\lambda_\mathrm{max}</math>, it is a function only of the temperature: | |||
| :<math>\lambda_\mathrm{max} = \frac{b}{T}</math> | |||
| where the constant, ''b'', known as Wien's displacement constant, is equal to {{val|2.8977685|(51)|e=-3|u=m K}}. | |||
| == See also == | |||
| Note that the peak intensity can be expressed in terms of intensity per unit wavelength or in terms of intensity per unit frequency. The form given in this section is in terms of intensity per unit wavelength, this form given in the Planck's Law section above was in terms of intensity per unit frequency. The wavelength at which the power per unit frequency is maximised is given by | |||
| * ] | |||
| :<math>\lambda'_\mathrm{max} = \frac{5.1 \times 10^{-3} \mbox{ m·K}}{T}</math>. | |||
| * ], a substance produced in 2014 and among the blackest known | |||
| * ], black body incandescence in a given chromaticity space | |||
| == References == | |||
| ===Stefan–Boltzmann law=== | |||
| {{Main|Stefan–Boltzmann law}} | |||
| This law states that the power emitted per unit area of the surface of a black body is directly proportional to the fourth power of its absolute temperature. That is | |||
| :<math>j^{\star} = \sigma T^4,</math> | |||
| where ''j''*is the total power radiated per unit area, ''T'' is the temperature (specified in a temperature system where 0 is at absolute zero, such as the kelvin scale,) and {{nowrap|''σ'' {{=}} {{val|5.67|e=-8|u=W m<sup>−2</sup> K<sup>−4</sup>}}}} is the ]. | |||
| === Citations === | |||
| ==Radiation emitted by a human body== | |||
| {{reflist|refs= | |||
| {| class="bordered infobox" style="width:22em" | |||
| | align="left"|] | |||
| |- | |||
| | align="left"|] | |||
| |- | |||
| |<small>Much of a person's energy is radiated away in the form of ] energy. Some materials are transparent to infrared light, while opaque to visible light (note the plastic bag). Other materials are transparent to visible light, while opaque or reflective to the infrared (note the man's glasses).</small> | |||
| |} | |||
| Black-body laws can be applied to human beings. For example, some of a person's energy is radiated away in the form of electromagnetic radiation, most of which is ]. | |||
| <ref name="Adkins"> | |||
| The net power radiated is the difference between the power emitted and the power absorbed: | |||
| {{cite book |author=Clement John Adkins |chapter=§4.1 The function of the second law |title=Equilibrium thermodynamics |chapter-url=https://books.google.com/books?id=FW4Oz48TWwQC&pg=PA50 |page=50 |isbn=978-0-521-27456-2 |edition=3rd |publisher=Cambridge University Press |year=1983}} | |||
| :<math>P_{net}=P_{emit}-P_{absorb}.</math> | |||
| </ref> | |||
| Applying the Stefan–Boltzmann law, | |||
| :<math>P_{net}=A\sigma \epsilon \left( T^4 - T_{0}^4 \right) \,</math>. | |||
| The total surface area of an adult is about 2 m², and the mid- and far-infrared ] of skin and most clothing is near unity, as it is for most nonmetallic surfaces.<ref>{{cite web | |||
| | author=Infrared Services | |||
| | title=Emissivity Values for Common Materials | |||
| | url=http://infrared-thermography.com/material-1.htm | |||
| | accessdate=2007-06-24}}</ref><ref>{{cite web | |||
| | author=Omega Engineering | |||
| | title=Emissivity of Common Materials | |||
| | url=http://www.omega.com/literature/transactions/volume1/emissivityb.html | |||
| | accessdate=2007-06-24}}</ref> Skin temperature is about 33°C,<ref>{{cite web | |||
| | last= Farzana|first= Abanty | |||
| | title=Temperature of a Healthy Human (Skin Temperature)|year=2001|work=The Physics Factbook | |||
| | url=http://hypertextbook.com/facts/2001/AbantyFarzana.shtml | |||
| | accessdate=2007-06-24}}</ref> but clothing reduces the surface temperature to about 28 °C when the ambient temperature is 20 °C.<ref>{{cite web | |||
| | author=Lee, B. | |||
| | title=Theoretical Prediction and Measurement of the Fabric Surface Apparent Temperature in a Simulated Man/Fabric/Environment System | |||
| | url=http://www.dsto.defence.gov.au/publications/2135/DSTO-TR-0849.pdf | |||
| | accessdate=2007-06-24}}</ref> Hence, the net radiative heat loss is about | |||
| :<math>P_{net} = 100 \ \mathrm{W} \,</math>. | |||
| The total energy radiated in one day is about 9 MJ (]s), or 2000 kcal (food ]s). ] for a 40-year-old male is about 35 kcal/(m<sup>2</sup>·h),<ref name="Harris1918">{{cite journal|author = Harris J, Benedict F|title = A Biometric Study of Human Basal Metabolism.|journal = Proc Natl Acad Sci USA| volume = 4|issue = 12| pages = 370–3|year = 1918|pmid = 16576330|doi = 10.1073/pnas.4.12.370|pmc = 1091498 | |||
| }}</ref> which is equivalent to 1700 kcal per day assuming the same 2 m<sup>2</sup> area. However, the mean metabolic rate of sedentary adults is about 50% to 70% greater than their basal rate.<ref>{{cite journal|author=Levine, J|title=Nonexercise activity thermogenesis (NEAT): environment and biology|journal=Am J Physiol Endocrinol Metab|volume=286|year=2004|pages=E675–E685|url=http://ajpendo.physiology.org/cgi/content/full/286/5/E675|doi=10.1152/ajpendo.00562.2003|pmid=15102614|issue=5}}</ref> | |||
| <ref name=Aller> | |||
| There are other important thermal loss mechanisms, including ] and ]. Conduction is negligible since the ] is much greater than unity. Evaporation (]) is only required if radiation and convection are insufficient to maintain a steady state temperature. Free convection rates are comparable, albeit somewhat lower, than radiative rates.<ref>{{cite web | |||
| {{cite book |title=Atoms, stars, and nebulae |url=https://books.google.com/books?id=HupvoeJDCGoC&pg=PA61 |page=61 |author=Lawrence Hugh Aller |publisher=Cambridge University Press |isbn=978-0-521-31040-6 |edition=3rd |year=1991}} | |||
| | author=DrPhysics.com | |||
| </ref> | |||
| | title=Heat Transfer and the Human Body | |||
| | url=http://www.drphysics.com/convection/convection.html | |||
| | accessdate=2007-06-24}}</ref> Thus, radiation accounts for about two-thirds of thermal energy loss in cool, still air. Given the approximate nature of many of the assumptions, this can only be taken as a crude estimate. Ambient air motion, causing forced convection, or evaporation reduces the relative importance of radiation as a thermal loss mechanism. | |||
| <ref name=Batrouni> | |||
| Also, applying ] to humans, one finds that the peak wavelength of light emitted by a person is | |||
| In simple cases the approach to equilibrium is governed by a ]. In others, the system may 'hang up' in a ], as stated by Adkins (1983) on page 10. For another example, see {{cite book |title=Equilibrium and non-equilibrium statistical thermodynamics |author1=Michel Le Bellac |author2=Fabrice Mortessagne |author3=Ghassan George Batrouni |page=8 |url=https://books.google.com/books?id=LZcdi4uzaWIC&pg=PA8 |isbn= 978-0521821438 |year=2004 |publisher=Cambridge University Press}} | |||
| :<math>\lambda_{peak} = \frac{2.898\times 10^6 \ \mathrm{K} \cdot \mathrm{nm}}{305 \ \mathrm{K}} = 9500 \ \mathrm{nm} \,</math>. | |||
| </ref> | |||
| This is why thermal imaging devices designed for human subjects are most sensitive to 7000–14000 nanometers wavelength. | |||
| <ref name=Bergmann> | |||
| ==Temperature relation between a planet and its star== | |||
| {{cite book |title=Optics of waves and particles |author1=Ludwig Bergmann |author2=Clemens Schaefer |author3=Heinz Niedrig |url=https://books.google.com/books?id=sJxv-yCSNEAC&pg=PA595 |page=595 |isbn=978-3-11-014318-8 |year=1999 |publisher=Walter de Gruyter |quote=Because the interaction of the photons with each other is negligible, a small amount of matter is necessary to establish thermodynamic equilibrium of heat radiation.}} | |||
| </ref> | |||
| <ref name=Bertotti> | |||
| Here is an application of black-body laws to roughly estimate the temperature of a planet. The surface may be warmer due to the ].<ref name="Cole">{{cite book|author=Cole, George H. A.; Woolfson, Michael M. | |||
| {{cite book |author1=B. Bertotti |author2=Paolo Farinella |author3=David Vokrouhlický |title=New Views of the Solar System |chapter=Figure 9.2: The temperature profile in the solar atmosphere |page=248 |chapter-url=https://books.google.com/books?id=i-YvHNPEqAIC&pg=PA248 |isbn=978-1-4020-1428-4 |year=2003 |publisher=Springer}} | |||
| |title=Planetary Science: The Science of Planets Around Stars (1st ed.) | |||
| </ref> | |||
| |publisher=Institute of Physics Publishing|year=2002|isbn=0-7503-0815-X|pages = 36–37, 380–382|url = http://books.google.com/books?id=Bgsy66mJ5mYC&pg=RA3-PA382&dq=black-body+emissivity+greenhouse+intitle:Planetary-Science+inauthor:cole&lr=&as_brr=0&ei=LrSOR9OYA4uotAP2ifyPBw&sig=mYO6KVgqvmYvdOu5-_qnQWCuVZk}}</ref> | |||
| <ref name=boson> | |||
| ===Factors=== | |||
| The fundamental bosons are the ], the vector bosons of the ], the ], and the ]. See {{cite book |title=Bose-Einstein condensation |url=https://books.google.com/books?id=suqJdr2pPIsC&pg=PA4 |page=4 |author1=Allan Griffin |author2=D. W. Snoke |author2-link=David Snoke|author3=S. Stringari |publisher=Cambridge University Press |year=1996 |isbn=978-0-521-58990-1}} | |||
| </ref> | |||
| <ref name=Brown> | |||
| ] intensity, from clouds, atmosphere and ground]] | |||
| See description of work by Richard Brown and his colleagues at the UK's National Physical Laboratory: {{cite journal | |||
| The temperature of a planet depends on a few factors: | |||
| |url= https://www.newscientist.com/article/dn3356-mini-craters-key-to-blackest-ever-black.html | |||
| |title=Mini craters key to 'blackest ever black' | |||
| |date=6 February 2003 | |||
| |author=Mick Hamer | |||
| |journal=New Scientist | |||
| }}</ref> | |||
| <ref name=Carr> | |||
| *Incident radiation (from the Sun, for example) | |||
| {{cite book |title=Beyond Extreme Physics: Cutting-edge science |chapter=Chapter 6: Quantum black holes |author1=Bernard J Carr |author2=Steven B Giddings |name-list-style=amp |chapter-url=https://books.google.com/books?id=N-K-q0_TexAC&pg=PA30 |page= |publisher=Rosen Publishing Group, Scientific American (COR) |isbn=978-1-4042-1402-6 |year=2008 |url=https://archive.org/details/beyondextremephy0000unse/page/30 }} | |||
| *Emitted radiation (for example ]) | |||
| </ref> | |||
| *The ] effect (the fraction of light a planet reflects) | |||
| *The ] (for planets with an atmosphere) | |||
| *Energy generated internally by a planet itself (due to ], ] and ]). | |||
| <ref name=Champion> | |||
| For the inner planets, incident and emitted radiation have the most significant impact on temperature. This derivation is concerned mainly with that. | |||
| {{cite book |title=MEMS and Microstructures in aerospace applications |author1=Robert Osiander |author2=M. Ann Garrison Darrin |author3=John Champion |url=https://books.google.com/books?id=DaqsgZ2HtIwC&pg=PA187 |page=187 |isbn=978-0-8247-2637-9 |year=2006 |publisher=CRC Press}} | |||
| </ref> | |||
| <ref name=Chun> | |||
| ===Derivation=== | |||
| {{cite journal |doi=10.1038/nnano.2008.29|title=Blacker than black|year=2008|last1=Chun|first1=Ai Lin|journal=Nature Nanotechnology|doi-access=free}} | |||
| </ref> | |||
| <ref name=Davies> | |||
| The ] gives the total ] (energy/second) the Sun is emitting: | |||
| {{cite journal |title=Thermodynamics of black holes |author=PCW Davies |journal=Rep Prog Phys |volume=41 |issue=8 |pages=1313–1355 |year=1978 |url=http://cosmos.asu.edu/publications/papers/ThermodynamicTheoryofBlackHoles%2034.pdf |doi=10.1088/0034-4885/41/8/004 |bibcode=1978RPPh...41.1313D |s2cid=250916407 |url-status=dead |archive-url=https://web.archive.org/web/20130510184530/http://cosmos.asu.edu/publications/papers/ThermodynamicTheoryofBlackHoles%2034.pdf |archive-date=2013-05-10 }} | |||
| </ref> | |||
| <ref name=emissivity> | |||
| ] | |||
| The emissivity of a surface in principle depends upon frequency, angle of view, and temperature. However, by definition, the radiation from a ''gray body'' is simply proportional to that of a black body at the same temperature, so its emissivity does not depend upon frequency (or, equivalently, wavelength). See {{cite book |title=Principles of heat transfer |author=Massoud Kaviany |chapter=Figure 4.3(b): Behaviors of a gray (no wavelength dependence), diffuse (no directional dependence) and opaque (no transmission) surface |page=381 |chapter-url=https://books.google.com/books?id=dKI4k-9jK88C&pg=PA381 |isbn=978-0-471-43463-4 |year=2002 |publisher=Wiley-IEEE}} and {{cite book |title=Encyclopedia of optical engineering, Volume 3 |author=Ronald G. Driggers |url=https://books.google.com/books?id=9ExHkgDv2z0C&pg=PA2303 |page=2303 |isbn=978-0-8247-4252-2 |publisher=CRC Press |year=2003}} | |||
| :<math>P_{S emt} = \left( \sigma T_{S}^4 \right) \left( 4 \pi R_{S}^2 \right) \qquad \qquad (1)</math> | |||
| </ref> | |||
| where | |||
| :<math>\sigma \,</math> is the ], | |||
| :<math>T_S \,</math> is the surface temperature of the Sun, and | |||
| :<math>R_S \,</math> is the radius of the Sun. | |||
| <ref name=Frolov> | |||
| The Sun emits that power equally in all directions. Because of this, the Earth is hit with only a tiny fraction of it. The power from the Sun that strikes the Earth (at the top of the atmosphere) is: | |||
| {{cite book |title=Introduction to Black Hole Physics |author1=Valeri P. Frolov |author2=Andrei Zelnikov |chapter-url=https://books.google.com/books?id=r_l5AK9DdXsC&pg=PA321 |page=321 |chapter=Equation 9.7.1 |isbn=978-0-19-969229-3 |year=2011 |publisher=Oxford University Press}} | |||
| </ref> | |||
| <ref name=Golay> | |||
| :<math>P_{SE} = P_{S emt} \left( \frac{\pi R_{E}^2}{4 \pi D^2} \right) \qquad \qquad (2)</math> | |||
| {{cite book |title=Introduction to astronomical photometry |author=M Golay |chapter-url=https://books.google.com/books?id=OmNuvvt31BkC&pg=PA82 |page=82 |chapter=Table IX: ''U-B'' Indices |isbn=978-90-277-0428-3 |year=1974 |publisher=Springer}} | |||
| where | |||
| </ref> | |||
| :<math>R_{E} \,</math> is the radius of the Earth and | |||
| :<math>D \,</math> is the ], the distance between the ] and the Earth. | |||
| <ref name=Gray> | |||
| Because of its high temperature, the sun emits to a large extent in the ultraviolet and visible (UV-Vis) frequency range. In this frequency range, the Earth reflects a fraction <math>\alpha</math> of this energy where <math>\alpha</math> is the ] or reflectance of the Earth in the UV-Vis range. In other words, the Earth absorbs a fraction <math>1-\alpha</math> of the sun's light, and reflects the rest. The power absorbed by the Earth and its atmosphere is then: | |||
| {{cite journal |author=David F Gray |journal=Publications of the Astronomical Society of the Pacific |volume=107 |pages=120–123 |date=February 1995 |title=Comparing the sun with other stars along the temperature coordinate |doi=10.1086/133525|bibcode = 1995PASP..107..120G |doi-access=free }} | |||
| </ref> | |||
| <ref name=gray_body>Some authors describe sources of infrared radiation with emissivity greater than approximately 0.99 as a black body. See {{cite web |title=What is a Blackbody and Infrared Radiation? |url=http://www.electro-optical.com/eoi_page.asp?h=What%20is%20a%20Blackbody%20and%20Infrared%20Radiation? |work=Education/Reference tab |publisher=Electro Optical Industries, Inc. |year=2008 |access-date=2019-06-10 |archive-url=https://web.archive.org/web/20160307024120/http://electro-optical.com/eoi_page.asp?h=what%20is%20a%20blackbody%20and%20infrared%20radiation%3F |archive-date=2016-03-07 |url-status=dead }}</ref> | |||
| :<math>P_{abs} = (1-\alpha)\,P_{SE} \qquad \qquad (3)</math> | |||
| <ref name=Green> | |||
| Even though the Earth only absorbs as a circular area <math>\pi R^2</math>, it emits equally in all directions as a sphere. If the Earth were a perfect black body, it would emit according to the Stephan-Boltzmann law | |||
| {{cite book |title=An introduction to the sun and stars |author1=Simon F. Green |author2=Mark H. Jones |author3=S. Jocelyn Burnell |url=https://books.google.com/books?id=lb5owLGIQGsC&pg=PA53 |pages=21–22, 53 |quote=A source in which photons are much more likely to interact with the material within the source than to escape is a condition for the formation of a black-body spectrum |isbn=978-0-521-54622-5 |year=2004 |publisher=Cambridge University Press}} | |||
| </ref> | |||
| <ref name=infinitesimal> | |||
| :<math>P_{emt\,bb} = \left( \sigma T_{E}^4 \right) \left( 4 \pi R_{E}^2 \right) \qquad \qquad (4)</math> | |||
| The notion of an infinitely thin layer was dropped by Planck. See {{harvnb|Planck|1914|page=10, footnote 2}}. | |||
| </ref> | |||
| <ref name=Kaviany> | |||
| where <math>T_{E} </math> is the temperature of the Earth. The Earth, since it is at a much lower temperature than the sun, emits mostly in the infrared (IR) portion of the spectrum. In this frequency range, it emits <math>\overline{\epsilon}</math> of the radiation that a black body would emit where <math>\overline{\epsilon}</math> is the average emissivity in the IR range. The power emitted by the Earth and its atmosphere is then: | |||
| {{cite book |title=Principles of heat transfer |author=Massoud Kaviany |chapter=Figure 4.3(b) Radiation properties of an opaque surface |page=381 |chapter-url=https://books.google.com/books?id=dKI4k-9jK88C&pg=PA381 |publisher=Wiley-IEEE |isbn=978-0-471-43463-4 |year=2002}} | |||
| </ref> | |||
| <ref name=Kelley> | |||
| :<math>P_{emt} = \overline{\epsilon}\,P_{emt\,bb} \qquad \qquad (5)</math> | |||
| {{cite book |title=Exploring Ancient Skies: A Survey of Ancient and Cultural Astronomy |author= David H. Kelley |author2= Eugene F. Milone |author3= Anthony F. (FRW) Aveni |url=https://books.google.com/books?id=ILBuYcGASxcC&pg=PA52 |page=52 |isbn=978-1-4419-7623-9 |publisher=Springer |year=2011 |edition=2nd}} | |||
| </ref> | |||
| <ref name=Kirchhoff> | |||
| Assuming that the Earth is in thermal equilibrium, the power absorbed must equal the power emitted: | |||
| Translated by F. Guthrie from ''Annalen der Physik'': '''109''', 275-301 (1860): {{cite journal |url=https://books.google.com/books?id=RVYEAAAAYAAJ&pg=PA1 |journal=The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science |title=On the relation between the radiating and absorbing powers of different bodies for light and heat |author=G. Kirchhoff |volume=20 |issue=130 |date=July 1860}} | |||
| </ref> | |||
| <ref name=Landsberg> | |||
| :<math>P_{abs}=P_{emt} \qquad \qquad (6)</math> | |||
| The approach to thermal equilibrium of the radiation in the cavity can be catalyzed by adding a small piece of matter capable of radiating and absorbing at all frequencies. See {{cite book |title= Thermodynamics and statistical mechanics |author=Peter Theodore Landsberg |url=https://books.google.com/books?id=0gnWL7tmxm0C&pg=PA209 |page=209 |isbn=978-0-486-66493-4 |publisher=Courier Dover Publications |edition=Reprint of Oxford University Press 1978 |year=1990 }} | |||
| </ref> | |||
| <ref name=Lang> | |||
| Substituting the expressions for solar and Earth power in equations 1-6 and simplifying yields: | |||
| {{cite book |title=Astrophysical formulae, Volume 1 |author=Kenneth R. Lang |url=https://books.google.com/books?id=HlGIXqzVEAgC&pg=PA23 |page=23 |isbn=978-3-540-29692-8 |edition=3rd |publisher=Birkhäuser |year=2006}} | |||
| </ref> | |||
| <ref name=Lewin> | |||
| :<math>T_E=T_S\sqrt{\frac{R_S\sqrt{\frac{1-\alpha}{\overline{\epsilon}}}}{2D}}</math> | |||
| {{cite book |chapter-url=https://books.google.com/books?id=ukItNVRRSp4C&pg=PA250 |pages= |author=Walter Lewin |author2=Warren Goldstein |title=For the love of physics |isbn=978-1-4391-0827-7 |year=2011 |publisher=Simon and Schuster |chapter=X-ray bursters! |url=https://archive.org/details/forloveofphysics0000lewi/page/251 }} | |||
| </ref> | |||
| <ref name=Lewis>{{cite journal |title=Materials keep a low profile |author=CF Lewis |date=June 1988 |journal=Mech. Eng. |pages=37–41 |url=http://www.cewriters.com/CEWritersSample_MaterialsFeature.pdf }}{{Dead link|date=August 2018 |bot=InternetArchiveBot |fix-attempted=yes }}</ref> | |||
| In other words, given the assumptions made, the temperature of Earth depends only on the surface temperature of the Sun, the radius of the Sun, the distance between Earth and the Sun, the albedo and the IR emissivity of the Earth. | |||
| <ref name=Mason> | |||
| ===Temperature of Earth=== | |||
| {{cite book |title=Astrophysics update, Volume 2 |author=TE Strohmayer |chapter=Neutron star structure and fundamental physics |editor=John W. Mason |chapter-url=https://books.google.com/books?id=SOzEHo1RteMC&pg=PA41 |page=41 |isbn=978-3-540-30312-1 |publisher=Birkhäuser |year=2006}} | |||
| </ref> | |||
| <ref name=Massoud> | |||
| If we substitute in the measured values for the Sun and Earth: | |||
| {{cite book |chapter-url=https://books.google.com/books?id=9KIp_fmC9A0C&pg=PA568 |page=568 |author=Mahmoud Massoud |title=Engineering thermofluids: thermodynamics, fluid mechanics, and heat transfer |chapter=§2.1 Blackbody radiation |isbn=978-3-540-22292-7 |publisher=Springer |year=2005}} | |||
| </ref> | |||
| <ref name=Mizuno> | |||
| :<math>T_{S} = 5778 \ \mathrm{K},</math><ref name="NASA"></ref> | |||
| {{cite journal | |||
| :<math>R_{S} = 6.96 \times 10^8 \ \mathrm{m},</math><ref name="NASA"/> | |||
| |author=K. Mizuno | |||
| :<math>D = 1.496 \times 10^{11} \ \mathrm{m},</math><ref name="NASA"/> | |||
| |title=A black body absorber from vertically aligned single-walled carbon nanotubes | |||
| :<math>\alpha = 0.306 \ </math><ref name="Cole"/> | |||
| |journal=] | |||
| |volume=106 |pages=6044–6077 | |||
| |year=2009 | |||
| |doi=10.1073/pnas.0900155106 | |||
| |pmid=19339498 | |||
| |issue=15 | |||
| |pmc=2669394 | |||
| |bibcode = 2009PNAS..106.6044M |display-authors=etal|doi-access=free | |||
| }} | |||
| </ref> | |||
| <ref name=Pearson> | |||
| If we set the average emissivity to unity, we calculate the "effective temperature" of the Earth to be: | |||
| A simple example is provided by {{cite book |title=The Person Guide to Objective Physics for the IIT-JEE |author=Srivastava M. K. |chapter=Cooling by radiation |chapter-url=https://books.google.com/books?id=FTpK4a4FTLQC&pg=PA610 |page=610 |publisher=Pearson Education India |year=2011 |isbn=978-81-317-5513-6}} | |||
| </ref> | |||
| <ref name=Quinn> | |||
| :<math>T_E = </math> 254.356 K or -18.8 °C. | |||
| {{cite book |title=Textile Futures |author=Bradley Quinn |year=2010 |isbn=978-1-84520-807-3 |publisher=Berg |url=https://books.google.com/books?id=e_wnynE954MC&pg=PA68 |page=68}} | |||
| </ref> | |||
| <ref name=Rechenberg> | |||
| This is the temperature that the Earth would be at if it radiated as a perfect black body in the infrared, ignoring greenhouse effects, and assuming an unchanging albedo. The Earth in fact radiates almost as a perfect black body in the infrared which will raise the estimated temperature a few degrees above the effective temperature. If we wish to estimate what the temperature of the Earth would be if it had no atmosphere, then we could take the albedo and emissivity of the moon as a good estimate. The albedo and emissivity of the moon are about 0.1054<ref name="Saari">{{cite journal |last1=Saari |first1=J. M. |last2=Shorthill |first2= R. W.|year=1972 |title=The Sunlit Lunar Surface. I. Albedo Studies and Full Moon |journal=The Moon |volume=5 |issue=1-2 |pages=161-178 |url=http://articles.adsabs.harvard.edu//full/1972Moon....5..161S/0000167.000.html |doi=10.1007/BF00562111 }}</ref> and 0.95<ref> Lunar and Planetary Science XXXVII (2006) 2406</ref> respectively, yielding an estimated temperature of about 1.36 °C. | |||
| An extensive historical discussion is found in {{cite book |title=The historical development of quantum theory |first1=Jagdish |last1=Mehra |author-link1=Jagdish Mehra |first2=Helmut |last2=Rechenberg |author-link2=Helmut Rechenberg |url=https://books.google.com/books?id=W5kyppVPyesC&pg=PA39 |pages=39 ''ff'' |isbn=978-0-387-95174-4 |year=2000 |publisher=Springer}} | |||
| </ref> | |||
| <ref name=Schutz> | |||
| Estimates of the Earth's average albedo vary in the range 0.3–0.4, resulting in different estimated effective temperatures. Estimates are often based on the ] (total insolation power density) rather than the temperature, size, and distance of the sun. For example, using 0.4 for albedo, and an insolation of 1400 W m<sup>−2</sup>), one obtains an effective temperature of about 245 K.<ref>{{cite book | |||
| {{cite book | |||
| |title = Space physics and space astronomy | |||
| | title = Gravity From the Group Up: An Introductory Guide to Gravity and General Relativity | |||
| |author = Michael D. Papagiannis | |||
| | isbn = 978-0-521-45506-0 | |||
| |publisher = Taylor & Francis | |||
| | |
| page = 304 | ||
| | last1 = Schutz | first1 = Bernard | |||
| |isbn = 9780677040004 | |||
| | publisher=Cambridge University Press | |||
| |pages = 10–11 | |||
| | edition=1st | |||
| |url = http://books.google.com/books?id=SpgOAAAAQAAJ&pg=PA10}}</ref> | |||
| | year=2004 | |||
| Similarly using albedo 0.3 and solar constant of 1372 W m<sup>−2</sup>), one obtains an effective temperature of 255 K.<ref>{{cite book | |||
| |title = Climate Change an Integrated Perspective | |||
| |author = Willem Jozef Meine Martens and Jan Rotmans | |||
| |publisher = Springer | |||
| |year = 1999 | |||
| |isbn = 9780792359968 | |||
| |pages = 52–55 | |||
| |url = http://books.google.com/books?id=o1SELkgK6PcC&pg=RA1-PA53&dq=Earth+effective-temperature+albedo+black-body+0.3&lr=&as_brr=3&as_pt=ALLTYPES&ei=TyDqSb_uOofmkATuyITyBg | |||
| }}</ref><ref>{{cite book | |||
| |title = Astrobiology: Future Perspectives | |||
| |chapter = The Prebiotic Atmosphere of the Earth | |||
| |author = F. Selsis | |||
| |editor = Pascale Ehrenfreund et al. | |||
| |publisher = Springer | |||
| |year = 2004 | |||
| |isbn = 9781402025877 | |||
| |pages = 279–280 | |||
| |url = http://books.google.com/books?id=bA_uR3iwzQUC&pg=PA279&dq=Earth+effective-temperature+albedo+black-body+0.3&lr=&as_brr=3&as_pt=ALLTYPES&ei=TyDqSb_uOofmkATuyITyBg#PPA280,M1 | |||
| }}</ref> | }}</ref> | ||
| <ref name=Shifman> | |||
| ==Doppler effect for a moving black body== | |||
| {{cite book |chapter= 6.2 Coling by Neutrino Emissions (pp. 2135-2136) – The Condensed Matter Physics of QCD |author1=Krishna Rajagopal |author2=Frank Wilczek |author-link2=Frank Wilczek |pages=2061–2151 |isbn=978-981-02-4969-4 |year=2001 |publisher=] |location=Singapore |editor=Mikhail A. Shifman |editor-link=Mikhail Shifman |title=At The Frontier of Particle Physics: Handbook of QCD (On the occasion of the 75th birthday of Professor Boris Ioffe) |volume=3 |quote=For the first 10<sup>5–6</sup> years of its life, the cooling of a neutron star is governed by the balance between heat capacity and the loss of heat by neutrino emission. ... Both the specific heat ''C<sub>V</sub>'' and the neutrino emission rate ''L<sub>ν</sub>'' are dominated by physics within ''T'' of the Fermi surface. ... The star will cool rapidly until its interior temperature is ''T'' < ''T<sub>c</sub> ~ ∆'', at which time the quark matter core will become inert and the further cooling history will be dominated by neutrino emission from the nuclear matter fraction of the star. |arxiv=hep-ph/0011333v2 |doi=10.1142/9789812810458_0043|citeseerx=10.1.1.344.2269 |s2cid=13606600 }} | |||
| </ref> | |||
| <ref name=Siegel> | |||
| The ] is the well known phenomenon describing how observed frequencies of light are "shifted" when a light source is moving relative to the observer. If ''f'' is the emitted frequency of a monochromatic light source, it will appear to have frequency ''f''' if it is moving relative to the observer: | |||
| {{cite book | |||
| :<math>f' = f \frac{1}{\sqrt{1-v^2/c^2}} (1 - \frac{v}{c} \cos \theta) </math> | |||
| | title = Thermal Radiation Heat Transfer; Volume 1 | |||
| where ''v'' is the velocity of the source in the observer's rest frame, ''θ'' is the angle between the velocity vector and the observer-source direction, and ''c'' is the ].<ref>The Doppler Effect, T. P. Gill, Logos Press, 1965</ref> This is the fully relativistic formula, and can be simplified for the special cases of objects moving directly towards (''θ'' = π) or away (''θ'' = 0) from the observer, and for speeds much less than ''c''. | |||
| | url = https://books.google.com/books?id=O389yQ0-fecC&pg=PA7 | |||
| | isbn = 978-1-56032-839-1 | |||
| | page = 7 | |||
| | last1 = Siegel | first1 = Robert | |||
| | last2 = Howell | first2 = John R. | |||
| | publisher=Taylor & Francis | |||
| | edition=4th | |||
| | year=2002 | |||
| }}</ref> | |||
| <ref name=Tipler> | |||
| To calculate the spectrum of a moving black body, then, it seems straightforward to simply apply this formula to each frequency of the blackbody spectrum. However, simply scaling each frequency like this is not enough. We also have to account for the finite size of the viewing aperture, because the solid angle receiving the light also undergoes a ]. (We can subsequently allow the aperture to be arbitrarily small, and the source arbitrarily far, but this cannot be ignored at the outset.) When this effect is included, it is found that a black body at temperature ''T'' that is receding with velocity ''v'' appears to have a spectrum identical to a stationary black body at temperature ''T''', given by:<ref>{{cite journal|doi=10.1119/1.11762|title=Relativistic transformations of light power|year=1979|last1=McKinley|first1=John M.|journal=American Journal of Physics|volume=47|pages=602}}</ref> | |||
| {{cite book |title=Physics for Scientists and Engineers, Parts 1-35; Part 39 |chapter-url=https://books.google.com/books?id=Gp2tzUhbqjMC&pg=PA1044 |page=1044 |chapter=Relative intensity of reflected and transmitted light |isbn=978-0-7167-3821-3 |year=1999 |edition=4th |publisher=Macmillan |author=Paul A. Tipler}} | |||
| :<math>T' = T \frac{1}{\sqrt{1-v^2/c^2}} (1 - \frac{v}{c} \cos \theta).</math> | |||
| </ref> | |||
| <ref name=Tolman> | |||
| For the case of a source moving directly towards or away from the observer, this reduces to | |||
| {{cite book |author=Richard Chace Tolman |author-link=Richard Chace Tolman |chapter=§103: Change of ''H'' with time as a result of collisions |title= The principles of statistical mechanics |pages= 455 ''ff'' |chapter-url=https://books.google.com/books?id=4TqQZo962s0C |isbn=978-0-486-63896-6 |edition=Reprint of 1938 Oxford University Press |publisher=Dover Publications |year=2010 |quote=...we can define a suitable quantity ''H'' to characterize the condition of a gas which a tendency to decrease with time as a result of collisions, unless the distribution of the molecules equilibrium. (p. 458)}} | |||
| :<math>T' = T \sqrt{\frac{c-v}{c+v}}.</math> | |||
| </ref> | |||
| Here ''v'' > 0 indicates a receding source, and ''v'' < 0 indicates an approaching source. | |||
| <ref name=UBV> | |||
| This is an important effect in astronomy, where the velocities of stars and galaxies can reach significant fractions of ''c''. An example is found in the ], which exhibits a dipole anisotropy from the Earth's motion relative to this blackbody radiation field. | |||
| Figure modeled after {{cite book |title=Introduction to Stellar Astrophysics: Basic stellar observations and data |author=E. Böhm-Vitense |chapter-url=https://books.google.com/books?id=JWrtilsCycQC&pg=PA26 |page=26 |chapter=Figure 4.9 |publisher=Cambridge University Press |isbn=978-0-521-34869-0 |year=1989}} | |||
| </ref> | |||
| <ref name=Venkanna> | |||
| ==See also== | |||
| {{cite book |title=Fundamentals of heat and mass transfer |author=BA Venkanna |chapter-url=https://books.google.com/books?id=IIIVHRirRgEC&pg=PA386 |pages=385–386 |chapter=§10.3.4 Absorptivity, reflectivity, and transmissivity |isbn=978-81-203-4031-2 |year=2010 |publisher=PHI Learning Pvt. Ltd.}} | |||
| {{colbegin|3}} | |||
| </ref> | |||
| <ref name=Vollmer> | |||
| * ] | |||
| {{cite book |title=Infrared Thermal Imaging: Fundamentals, Research and Applications |chapter=Figure 1.38: Some examples for temperature dependence of emissivity for different materials |chapter-url=https://books.google.com/books?id=nAIZb8-05IwC&pg=PA45 |page=45 |author1=M Vollmer |author2=K-P Mõllmann |isbn=978-3-527-63087-5 |year=2011 |publisher=John Wiley & Sons}} | |||
| * ] | |||
| </ref> | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| {{colend}} | |||
| <ref name=Wald> | |||
| ==Notes== | |||
| {{cite book |chapter=The thermodynamics of black holes |author=Robert M Wald |chapter-url=https://books.google.com/books?id=ZDtxnw-b1xEC&pg=PA1 |pages=1–38 |editor1=Andrés Gomberoff |editor2=Donald Marolf |title=Lectures on quantum gravity |isbn=978-0-387-23995-8 |year=2005 |publisher=]}} | |||
| <references group="nb" /> | |||
| </ref> | |||
| <ref name=Wald2> | |||
| ==References== | |||
| {{cite book |editor1=Andrés Gomberoff |editor2=Donald Marolf |author=Robert M Wald |chapter-url=https://books.google.com/books?id=ZDtxnw-b1xEC&pg=PA28 |chapter=The thermodynamics of black holes (pp. 1–38) |title=Lectures on Quantum Gravity |quote=... no results on black hole thermodynamics have been subject to any experimental or observational tests ... |year=2005 |isbn=978-0-387-23995-8 |page=28 |publisher=]}} | |||
| {{Reflist|2}} | |||
| </ref> | |||
| <ref name=White> | |||
| ===Other textbooks=== | |||
| {{cite journal|author=White, M. |year=1999 |title=Anisotropies in the CMB |journal= Proceedings of the Los Angeles Meeting, DPF 99. UCLA. |url=http://www.dpf99.library.ucla.edu/session9/white0910.pdf}} See also . | |||
| *{{cite book|author=Kroemer, Herbert; Kittel, Charles | |||
| </ref> | |||
| |title=Thermal Physics |edition=2nd|publisher=W. H. Freeman Company|year=1980 | |||
| |isbn=0716710889}} | |||
| *{{cite book|author=Tipler, Paul; Llewellyn, Ralph | |||
| |title=Modern Physics |edition=4th|publisher=W. H. Freeman|year=2002|isbn=0716743450}} | |||
| <ref name=Yang> | |||
| ==External links== | |||
| {{cite journal |author=Zu-Po Yang |s2cid= 7412160 |title= Experimental observation of an extremely dark material made by a low-density nanotube array |journal=Nano Letters |volume=8 |issue=2|pages= 446–451 |year=2008 |doi=10.1021/nl072369t |bibcode = 2008NanoL...8..446Y |pmid=18181658|display-authors=etal}} | |||
| * Interactive calculator with Doppler Effect. Includes most systems of units. | |||
| </ref> | |||
| * - From Hyperphysics | |||
| * | |||
| * | |||
| * by Jeff Bryant, ], 2007. | |||
| * | |||
| <ref name=Zee> | |||
| {{DEFAULTSORT:Black Body}} | |||
| Corrections to the spectrum do arise related to boundary conditions at the walls, curvature, and topology, particularly for wavelengths comparable to the cavity dimensions; see {{cite book |title=Cavity-enhanced spectroscopies |url=https://books.google.com/books?id=OuLILePVdJQC&pg=PA202 |page=202 |author1=Roger Dale Van Zee |author2=J. Patrick Looney |isbn=978-0-12-475987-9 |year=2002 |publisher=Academic Press}} | |||
| <!--Categories--> | |||
| </ref> | |||
| ] | |||
| }} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| === Bibliography === | |||
| <!--Interwiki--> | |||
| {{refbegin|30em}} | |||
| * {{cite book | |||
| |last1=Chandrasekhar |first1=S. | |||
| |author1-link=Subrahmanyan Chandrasekhar | |||
| |year=1950 | |||
| |title=Radiative Transfer | |||
| |publisher=] | |||
| }} | |||
| * {{cite book | |||
| |last1=Goody |first1=R. M. | |||
| |last2=Yung |first2=Y. L. | |||
| |author2-link=Yuk L. Yung | |||
| |year=1989 | |||
| |title=Atmospheric Radiation: Theoretical Basis | |||
| |edition=2nd | |||
| |publisher=] | |||
| |isbn=978-0-19-510291-8 | |||
| }} | |||
| * {{cite book | |||
| |last1=Hermann | |||
| |first1=A. | |||
| |author1-link=Armin Hermann | |||
| |others=Nash, C.W. (transl.) | |||
| |year=1971 | |||
| |title=The Genesis of Quantum Theory | |||
| |publisher=] | |||
| |isbn=978-0-262-08047-7 | |||
| |url=https://archive.org/details/genesisofquantum00herm | |||
| }} a translation of ''Frühgeschichte der Quantentheorie (1899–1913)'', Physik Verlag, Mosbach/Baden. | |||
| * {{cite book | |||
| |last1=Kangro |first1=H. | |||
| |author1-link=Hans Kangro | |||
| |year=1976 | |||
| |title=Early History of Planck's Radiation Law | |||
| |publisher=] | |||
| |isbn=978-0-85066-063-0 | |||
| }} | |||
| * {{cite journal | |||
| |last1=Kirchhoff |first1=G. | |||
| |author1-link=Gustav Kirchhoff | |||
| |year=1860a | |||
| |title=Über die Fraunhofer'schen Linien | |||
| |journal=] | |||
| |pages=662–665 | |||
| }} | |||
| * {{cite journal | |||
| |last1=Kirchhoff |first1=G. | |||
| |author1-link=Gustav Kirchhoff | |||
| |date= 1860b | |||
| |title=Über den Zusammenhang zwischen Emission und Absorption von Licht und Wärme | |||
| |journal=] | |||
| |pages=783–787 | |||
| }} | |||
| * {{cite journal | |||
| |last1=Kirchhoff |first1=G. | |||
| |author1-link=Gustav Kirchhoff | |||
| |year=1860c | |||
| |title=Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme and Licht | |||
| |journal=] | |||
| |volume=185 | |||
| |issue=2 | |||
| |pages=275–301 | |||
| |url=https://books.google.com/books?id=RVYEAAAAYAAJ&pg=PA1 | |||
| |doi=10.1002/andp.18601850205 | |||
| |bibcode = 1860AnP...185..275K |doi-access=free | |||
| }} Translated by Guthrie, F. as {{cite journal | |||
| |last1=Kirchhoff |first1=G. | |||
| |year=1860 | |||
| |title=On the relation between the radiating and absorbing powers of different bodies for light and heat | |||
| |journal=] | |||
| |series=Series 4 |volume=20 |pages=1–21 | |||
| |url=https://books.google.com/books?id=RVYEAAAAYAAJ&pg=PA1 | |||
| }} | |||
| * {{cite book | |||
| | last = Kirchhoff | |||
| | first = G. | |||
| | author-link = Gustav Kirchhoff | |||
| | title = Gessamelte Abhandlungen | |||
| | place = Leipzig | |||
| | publisher = Johann Ambrosius Barth | |||
| | orig-year = 1862 | |||
| | year = 1882 | |||
| | chapter = Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme und Licht | |||
| | pages = 571–598 | |||
| }} | |||
| * {{cite book | |||
| |last1=Kondepudi |first1=D. | |||
| |author1-link=Dilip Kondepudi | |||
| |last2=Prigogine |first2=I. | |||
| |author2-link=Ilya Prigogine | |||
| |year=1998 | |||
| |title=Modern Thermodynamics. From Heat Engines to Dissipative Structures | |||
| |url=https://archive.org/details/modernthermodyna0000kond |url-access=registration |publisher=] | |||
| |isbn=978-0-471-97393-5 | |||
| }} | |||
| * {{cite book | |||
| |last1=Kragh |first1=H. | |||
| |author1-link=Helge Kragh | |||
| |year=1999 | |||
| |title=Quantum Generations: a History of Physics in the Twentieth Century | |||
| |url=https://archive.org/details/quantumgeneratio0000krag |url-access=registration |publisher=] | |||
| |isbn=978-0-691-01206-3 | |||
| }} | |||
| * {{cite book | |||
| |last1=Kuhn |first1=T. S. | |||
| |author1-link=Thomas Kuhn | |||
| |year=1978 | |||
| |title=Black–Body Theory and the Quantum Discontinuity | |||
| |publisher=] | |||
| |isbn=978-0-19-502383-1 | |||
| }} | |||
| * {{cite book | |||
| |last1=Loudon |first1=R. | |||
| |author1-link=Rodney Loudon | |||
| |year=2000 | |||
| |orig-year=1973 | |||
| |title=The Quantum Theory of Light | |||
| |publisher=] | |||
| |edition=third | |||
| |isbn=978-0-19-850177-0 | |||
| }} | |||
| * {{cite journal | |||
| |last1=Lummer |first1=O. | |||
| |author1-link=Otto Lummer | |||
| |last2=Kurlbaum |first2=F. | |||
| |author2-link=Ferdinand Kurlbaum | |||
| |year=1898 | |||
| |title=Der electrisch geglühte "absolut schwarze" Körper und seine Temperaturmessung | |||
| |journal=] | |||
| |volume=17 | |||
| |pages=106–111 | |||
| }} | |||
| * {{cite journal | |||
| |last1=Lummer |first1=O. | |||
| |author1-link=Otto Lummer | |||
| |last2=Kurlbaum |first2=F. | |||
| |author2-link=Ferdinand Kurlbaum | |||
| |year=1901 | |||
| |title=Der elektrisch geglühte "schwarze" Körper | |||
| |journal=] | |||
| |volume=310 | |||
| |issue=8 | |||
| |pages=829–836 | |||
| |doi=10.1002/andp.19013100809 | |||
| |bibcode = 1901AnP...310..829L |url=https://zenodo.org/record/1424003 | |||
| }} | |||
| * {{cite book | |||
| |last1=Mandel |first1=L. | |||
| |author1-link=Leonard Mandel | |||
| |last2=Wolf |first2=E. | |||
| |author2-link=Emil Wolf | |||
| |year=1995 | |||
| |title=Optical Coherence and Quantum Optics | |||
| |url=https://archive.org/details/opticalcoherence0000mand |url-access=registration |publisher=] | |||
| |isbn=978-0-521-41711-2 | |||
| }} | |||
| * {{cite book | |||
| |last1=Mehra |first1=J. | |||
| |author1-link=Jagdish Mehra | |||
| |last2=Rechenberg |first2=H. | |||
| |author2-link=Helmut Rechenberg | |||
| |year=1982 | |||
| |title=The Historical Development of Quantum Theory | |||
| |volume=1, part 1 | |||
| |publisher=] | |||
| |isbn=978-0-387-90642-3 | |||
| }} | |||
| * {{cite book | |||
| |last1=Mihalas |first1=D. | |||
| |author1-link=Dimitri Mihalas | |||
| |last2=Weibel-Mihalas |first2=B. | |||
| |year=1984 | |||
| |title=Foundations of Radiation Hydrodynamics | |||
| |publisher=] | |||
| |isbn=978-0-19-503437-0 | |||
| }} | |||
| * {{cite journal | |||
| |last1=Milne |first1=E.A. | |||
| |author1-link=Edward Arthur Milne | |||
| |year=1930 | |||
| |title=Thermodynamics of the Stars | |||
| |journal=] | |||
| |volume=3, part 1 | |||
| |pages=63–255 | |||
| }} | |||
| * {{cite book | |||
| |last1=Planck |first1=M. | |||
| |author1-link=Max Planck | |||
| |others=Masius, M. (transl.) | |||
| |year=1914 | |||
| |title=The Theory of Heat Radiation | |||
| |publisher=] | |||
| |url=https://archive.org/details/theheatradiation00planrich | |||
| |edition=2nd | |||
| |ol=7154661M | |||
| }} | |||
| * {{cite book | |||
| |last1=Rybicki |first1=G. B. | |||
| |last2=Lightman |first2=A. P. | |||
| |author2-link=Alan Lightman | |||
| |year=1979 | |||
| |title=Radiative Processes in Astrophysics | |||
| |url=https://books.google.com/books?id=LtdEjNABMlsC | |||
| |publisher=] | |||
| |isbn=978-0-471-82759-7 | |||
| }} | |||
| * {{cite book | |||
| |last1=Schirrmacher |first1=A. | |||
| |author1-link=Arne Schirrmacher | |||
| |year=2001 | |||
| |title=Experimenting theory: the proofs of Kirchhoff's radiation law before and after Planck | |||
| |publisher=] | |||
| }} | |||
| * {{cite journal | |||
| |last1=Stewart |first1=B. | |||
| |author1-link=Balfour Stewart | |||
| |year=1858 | |||
| |title=An account of some experiments on radiant heat | |||
| |journal=] | |||
| |volume=22 |pages=1–20 | |||
| |doi=10.1017/S0080456800031288 | |||
| |s2cid=122316368 | |||
| |url=https://zenodo.org/record/2137146 | |||
| }} | |||
| {{refend}} | |||
| == External links == | |||
| ] | |||
| * {{cite web |title= Blacker than black |url= http://www.nasa.gov/topics/technology/features/new-nano.html |publisher= ] |first= Lori J. |last= Keesey |date= Dec 12, 2010 |quote= Engineers now developing a blacker-than pitch material that will help scientists gather hard-to-obtain scientific measurements... nanotech-based material now being developed by a team of 10 technologists at the NASA ] |access-date= 1 February 2012 |archive-date= 14 June 2020 |archive-url= https://web.archive.org/web/20200614004129/https://www.nasa.gov/topics/technology/features/new-nano.html |url-status= dead }} | |||
| ] | |||
| ] | |||
| {{Authority control}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 03:22, 29 November 2024
Idealized physical body that absorbs all incident electromagnetic radiation "Black bodies" redirects here. Not to be confused with Black Bodies (film).

A black body or blackbody is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. The radiation emitted by a black body in thermal equilibrium with its environment is called black-body radiation. The name "black body" is given because it absorbs all colors of light. In contrast, a white body is one with a "rough surface that reflects all incident rays completely and uniformly in all directions."
A black body in thermal equilibrium (that is, at a constant temperature) emits electromagnetic black-body radiation. The radiation is emitted according to Planck's law, meaning that it has a spectrum that is determined by the temperature alone (see figure at right), not by the body's shape or composition.
An ideal black body in thermal equilibrium has two main properties:
- It is an ideal emitter: at every frequency, it emits as much or more thermal radiative energy as any other body at the same temperature.
- It is a diffuse emitter: measured per unit area perpendicular to the direction, the energy is radiated isotropically, independent of direction.
Real materials emit energy at a fraction—called the emissivity—of black-body energy levels. By definition, a black body in thermal equilibrium has an emissivity ε = 1. A source with a lower emissivity, independent of frequency, is often referred to as a gray body. Constructing black bodies with an emissivity as close to 1 as possible remains a topic of current interest.
In astronomy, the radiation from stars and planets is sometimes characterized in terms of an effective temperature, the temperature of a black body that would emit the same total flux of electromagnetic energy.
Definition
Isaac Newton introduced the notion of a black body in his 1704 book Opticks, with query 6 of the book stating:
Do not black Bodies conceive heat more easily from Light than those of other Colours do, by reason that the Light falling on them is not reflected outwards, but enters into the Bodies, and is often reflected and refracted within them, until it be stifled and lost?
The idea of a black body originally was introduced by Gustav Kirchhoff in 1860 as follows:
...the supposition that bodies can be imagined which, for infinitely small thicknesses, completely absorb all incident rays, and neither reflect nor transmit any. I shall call such bodies perfectly black, or, more briefly, black bodies.
A more modern definition drops the reference to "infinitely small thicknesses":
An ideal body is now defined, called a blackbody. A blackbody allows all incident radiation to pass into it (no reflected energy) and internally absorbs all the incident radiation (no energy transmitted through the body). This is true for radiation of all wavelengths and for all angles of incidence. Hence the blackbody is a perfect absorber for all incident radiation.
Idealizations
This section describes some concepts developed in connection with black bodies.

Cavity with a hole
A widely used model of a black surface is a small hole in a cavity with walls that are opaque to radiation. Radiation incident on the hole will pass into the cavity, and is very unlikely to be re-emitted if the cavity is large. Lack of any re-emission, means that the hole is behaving like a perfect black surface. The hole is not quite a perfect black surface—in particular, if the wavelength of the incident radiation is greater than the diameter of the hole, part will be reflected. Similarly, even in perfect thermal equilibrium, the radiation inside a finite-sized cavity will not have an ideal Planck spectrum for wavelengths comparable to or larger than the size of the cavity.
Suppose the cavity is held at a fixed temperature T and the radiation trapped inside the enclosure is at thermal equilibrium with the enclosure. The hole in the enclosure will allow some radiation to escape. If the hole is small, radiation passing in and out of the hole has negligible effect upon the equilibrium of the radiation inside the cavity. This escaping radiation will approximate black-body radiation that exhibits a distribution in energy characteristic of the temperature T and does not depend upon the properties of the cavity or the hole, at least for wavelengths smaller than the size of the hole. See the figure in the Introduction for the spectrum as a function of the frequency of the radiation, which is related to the energy of the radiation by the equation E = hf, with E = energy, h = Planck constant, f = frequency.
At any given time the radiation in the cavity may not be in thermal equilibrium, but the second law of thermodynamics states that if left undisturbed it will eventually reach equilibrium, although the time it takes to do so may be very long. Typically, equilibrium is reached by continual absorption and emission of radiation by material in the cavity or its walls. Radiation entering the cavity will be "thermalized" by this mechanism: the energy will be redistributed until the ensemble of photons achieves a Planck distribution. The time taken for thermalization is much faster with condensed matter present than with rarefied matter such as a dilute gas. At temperatures below billions of Kelvin, direct photon–photon interactions are usually negligible compared to interactions with matter. Photons are an example of an interacting boson gas, and as described by the H-theorem, under very general conditions any interacting boson gas will approach thermal equilibrium.
Transmission, absorption, and reflection
A body's behavior with regard to thermal radiation is characterized by its transmission τ, absorption α, and reflection ρ.
The boundary of a body forms an interface with its surroundings, and this interface may be rough or smooth. A nonreflecting interface separating regions with different refractive indices must be rough, because the laws of reflection and refraction governed by the Fresnel equations for a smooth interface require a reflected ray when the refractive indices of the material and its surroundings differ. A few idealized types of behavior are given particular names:
An opaque body is one that transmits none of the radiation that reaches it, although some may be reflected. That is, τ = 0 and α + ρ = 1.
A transparent body is one that transmits all the radiation that reaches it. That is, τ = 1 and α = ρ = 0.
A grey body is one where α, ρ and τ are constant for all wavelengths; this term also is used to mean a body for which α is temperature- and wavelength-independent.
A white body is one for which all incident radiation is reflected uniformly in all directions: τ = 0, α = 0, and ρ = 1.
For a black body, τ = 0, α = 1, and ρ = 0. Planck offers a theoretical model for perfectly black bodies, which he noted do not exist in nature: besides their opaque interior, they have interfaces that are perfectly transmitting and non-reflective.
Kirchhoff's perfect black bodies
Kirchhoff in 1860 introduced the theoretical concept of a perfect black body with a completely absorbing surface layer of infinitely small thickness, but Planck noted some severe restrictions upon this idea. Planck noted three requirements upon a black body: the body must (i) allow radiation to enter but not reflect; (ii) possess a minimum thickness adequate to absorb the incident radiation and prevent its re-emission; (iii) satisfy severe limitations upon scattering to prevent radiation from entering and bouncing back out. As a consequence, Kirchhoff's perfect black bodies that absorb all the radiation that falls on them cannot be realized in an infinitely thin surface layer, and impose conditions upon scattering of the light within the black body that are difficult to satisfy.
Realizations
A realization of a black body refers to a real world, physical embodiment. Here are a few.
Cavity with a hole
In 1898, Otto Lummer and Ferdinand Kurlbaum published an account of their cavity radiation source. Their design has been used largely unchanged for radiation measurements to the present day. It was a hole in the wall of a platinum box, divided by diaphragms, with its interior blackened with iron oxide. It was an important ingredient for the progressively improved measurements that led to the discovery of Planck's law. A version described in 1901 had its interior blackened with a mixture of chromium, nickel, and cobalt oxides. See also Hohlraum.
Near-black materials
There is interest in blackbody-like materials for camouflage and radar-absorbent materials for radar invisibility. They also have application as solar energy collectors, and infrared thermal detectors. As a perfect emitter of radiation, a hot material with black body behavior would create an efficient infrared heater, particularly in space or in a vacuum where convective heating is unavailable. They are also useful in telescopes and cameras as anti-reflection surfaces to reduce stray light, and to gather information about objects in high-contrast areas (for example, observation of planets in orbit around their stars), where blackbody-like materials absorb light that comes from the wrong sources.
It has long been known that a lamp-black coating will make a body nearly black. An improvement on lamp-black is found in manufactured carbon nanotubes. Nano-porous materials can achieve refractive indices nearly that of vacuum, in one case obtaining average reflectance of 0.045%. In 2009, a team of Japanese scientists created a material called nanoblack which is close to an ideal black body, based on vertically aligned single-walled carbon nanotubes. This absorbs between 98% and 99% of the incoming light in the spectral range from the ultra-violet to the far-infrared regions.
Other examples of nearly perfect black materials are super black, prepared by chemically etching a nickel–phosphorus alloy, vertically aligned carbon nanotube arrays (like Vantablack) and flower carbon nanostructures; all absorb 99.9% of light or more.
Stars and planets
For more about the UBV color index, see Photometric system.
A star or planet often is modeled as a black body, and electromagnetic radiation emitted from these bodies as black-body radiation. The figure shows a highly schematic cross-section to illustrate the idea. The photosphere of the star, where the emitted light is generated, is idealized as a layer within which the photons of light interact with the material in the photosphere and achieve a common temperature T that is maintained over a long period of time. Some photons escape and are emitted into space, but the energy they carry away is replaced by energy from within the star, so that the temperature of the photosphere is nearly steady. Changes in the core lead to changes in the supply of energy to the photosphere, but such changes are slow on the time scale of interest here. Assuming these circumstances can be realized, the outer layer of the star is somewhat analogous to the example of an enclosure with a small hole in it, with the hole replaced by the limited transmission into space at the outside of the photosphere. With all these assumptions in place, the star emits black-body radiation at the temperature of the photosphere.
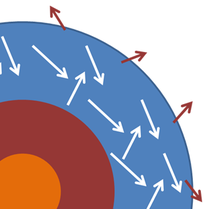
Using this model the effective temperature of stars is estimated, defined as the temperature of a black body that yields the same surface flux of energy as the star. If a star were a black body, the same effective temperature would result from any region of the spectrum. For example, comparisons in the B (blue) or V (visible) range lead to the so-called B-V color index, which increases the redder the star, with the Sun having an index of +0.648 ± 0.006. Combining the U (ultraviolet) and the B indices leads to the U-B index, which becomes more negative the hotter the star and the more the UV radiation. Assuming the Sun is a type G2 V star, its U-B index is +0.12. The two indices for two types of most common star sequences are compared in the figure (diagram) with the effective surface temperature of the stars if they were perfect black bodies. There is a rough correlation. For example, for a given B-V index measurement, the curves of both most common sequences of star (the main sequence and the supergiants) lie below the corresponding black-body U-B index that includes the ultraviolet spectrum, showing that both groupings of star emit less ultraviolet light than a black body with the same B-V index. It is perhaps surprising that they fit a black body curve as well as they do, considering that stars have greatly different temperatures at different depths. For example, the Sun has an effective temperature of 5780 K, which can be compared to the temperature of its photosphere (the region generating the light), which ranges from about 5000 K at its outer boundary with the chromosphere to about 9500 K at its inner boundary with the convection zone approximately 500 km (310 mi) deep.

Black holes
See also: Hawking radiationA black hole is a region of spacetime from which nothing escapes. Around a black hole there is a mathematically defined surface called an event horizon that marks the point of no return. It is called "black" because it absorbs all the light that hits the horizon, reflecting nothing, making it almost an ideal black body (radiation with a wavelength equal to or larger than the diameter of the hole may not be absorbed, so black holes are not perfect black bodies). Physicists believe that to an outside observer, black holes have a non-zero temperature and emit black-body radiation, radiation with a nearly perfect black-body spectrum, ultimately evaporating. The mechanism for this emission is related to vacuum fluctuations in which a virtual pair of particles is separated by the gravity of the hole, one member being sucked into the hole, and the other being emitted. The energy distribution of emission is described by Planck's law with a temperature T:
where c is the speed of light, ℏ is the reduced Planck constant, kB is the Boltzmann constant, G is the gravitational constant and M is the mass of the black hole. These predictions have not yet been tested either observationally or experimentally.
Cosmic microwave background radiation
See also: Big Bang and Cosmic microwave background radiationThe Big Bang theory is based upon the cosmological principle, which states that on large scales the Universe is homogeneous and isotropic. According to theory, the Universe approximately a second after its formation was a near-ideal black body in thermal equilibrium at a temperature above 10 K. The temperature decreased as the Universe expanded and the matter and radiation in it cooled. The cosmic microwave background radiation observed today is "the most perfect black body ever measured in nature". It has a nearly ideal Planck spectrum at a temperature of about 2.7 K. It departs from the perfect isotropy of true black-body radiation by an observed anisotropy that varies with angle on the sky only to about one part in 100,000.
Radiative cooling

The integration of Planck's law over all frequencies provides the total energy per unit of time per unit of surface area radiated by a black body maintained at a temperature T, and is known as the Stefan–Boltzmann law:
where σ is the Stefan–Boltzmann constant, σ ≈ 5.67×10 W⋅m⋅K To remain in thermal equilibrium at constant temperature T, the black body must absorb or internally generate this amount of power P over the given area A.
The cooling of a body due to thermal radiation is often approximated using the Stefan–Boltzmann law supplemented with a "gray body" emissivity ε ≤ 1 (P/A = εσT). The rate of decrease of the temperature of the emitting body can be estimated from the power radiated and the body's heat capacity. This approach is a simplification that ignores details of the mechanisms behind heat redistribution (which may include changing composition, phase transitions or restructuring of the body) that occur within the body while it cools, and assumes that at each moment in time the body is characterized by a single temperature. It also ignores other possible complications, such as changes in the emissivity with temperature, and the role of other accompanying forms of energy emission, for example, emission of particles like neutrinos.
If a hot emitting body is assumed to follow the Stefan–Boltzmann law and its power emission P and temperature T are known, this law can be used to estimate the dimensions of the emitting object, because the total emitted power is proportional to the area of the emitting surface. In this way it was found that X-ray bursts observed by astronomers originated in neutron stars with a radius of about 10 km, rather than black holes as originally conjectured. An accurate estimate of size requires some knowledge of the emissivity, particularly its spectral and angular dependence.
See also
- Kirchhoff's law of thermal radiation
- Vantablack, a substance produced in 2014 and among the blackest known
- Planckian locus, black body incandescence in a given chromaticity space
References
Citations
- Planck 1914, pp. 9–10
- Mahmoud Massoud (2005). "§2.1 Blackbody radiation". Engineering thermofluids: thermodynamics, fluid mechanics, and heat transfer. Springer. p. 568. ISBN 978-3-540-22292-7.
- The emissivity of a surface in principle depends upon frequency, angle of view, and temperature. However, by definition, the radiation from a gray body is simply proportional to that of a black body at the same temperature, so its emissivity does not depend upon frequency (or, equivalently, wavelength). See Massoud Kaviany (2002). "Figure 4.3(b): Behaviors of a gray (no wavelength dependence), diffuse (no directional dependence) and opaque (no transmission) surface". Principles of heat transfer. Wiley-IEEE. p. 381. ISBN 978-0-471-43463-4. and Ronald G. Driggers (2003). Encyclopedia of optical engineering, Volume 3. CRC Press. p. 2303. ISBN 978-0-8247-4252-2.
- Some authors describe sources of infrared radiation with emissivity greater than approximately 0.99 as a black body. See "What is a Blackbody and Infrared Radiation?". Education/Reference tab. Electro Optical Industries, Inc. 2008. Archived from the original on 7 March 2016. Retrieved 10 June 2019.
- ^ Chun, Ai Lin (2008). "Blacker than black". Nature Nanotechnology. doi:10.1038/nnano.2008.29.
- Bochner, Salomon (1981). Role of Mathematics in the Rise of Science. Princeton, NJ: Princeton Univ. Pr. pp. 221, 347. ISBN 978-0-691-08028-4.
- Rowlands, Peter (2017). Newton - Innovation And Controversy. World Scientific Publishing. p. 69. ISBN 9781786344045.
- Translated by F. Guthrie from Annalen der Physik: 109, 275-301 (1860): G. Kirchhoff (July 1860). "On the relation between the radiating and absorbing powers of different bodies for light and heat". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 20 (130).
- The notion of an infinitely thin layer was dropped by Planck. See Planck 1914, p. 10, footnote 2.
- ^ Siegel, Robert; Howell, John R. (2002). Thermal Radiation Heat Transfer; Volume 1 (4th ed.). Taylor & Francis. p. 7. ISBN 978-1-56032-839-1.
- ^ Corrections to the spectrum do arise related to boundary conditions at the walls, curvature, and topology, particularly for wavelengths comparable to the cavity dimensions; see Roger Dale Van Zee; J. Patrick Looney (2002). Cavity-enhanced spectroscopies. Academic Press. p. 202. ISBN 978-0-12-475987-9.
- Clement John Adkins (1983). "§4.1 The function of the second law". Equilibrium thermodynamics (3rd ed.). Cambridge University Press. p. 50. ISBN 978-0-521-27456-2.
- In simple cases the approach to equilibrium is governed by a relaxation time. In others, the system may 'hang up' in a metastable state, as stated by Adkins (1983) on page 10. For another example, see Michel Le Bellac; Fabrice Mortessagne; Ghassan George Batrouni (2004). Equilibrium and non-equilibrium statistical thermodynamics. Cambridge University Press. p. 8. ISBN 978-0521821438.
- The approach to thermal equilibrium of the radiation in the cavity can be catalyzed by adding a small piece of matter capable of radiating and absorbing at all frequencies. See Peter Theodore Landsberg (1990). Thermodynamics and statistical mechanics (Reprint of Oxford University Press 1978 ed.). Courier Dover Publications. p. 209. ISBN 978-0-486-66493-4.
- Planck 1914, p. 44, §52
- Loudon 2000, Chapter 1
- Mandel & Wolf 1995, Chapter 13
- Robert Karplus* and Maurice Neuman, "The Scattering of Light by Light", Phys. Rev. 83, 776–784 (1951)
-
Ludwig Bergmann; Clemens Schaefer; Heinz Niedrig (1999). Optics of waves and particles. Walter de Gruyter. p. 595. ISBN 978-3-11-014318-8.
Because the interaction of the photons with each other is negligible, a small amount of matter is necessary to establish thermodynamic equilibrium of heat radiation.
- The fundamental bosons are the photon, the vector bosons of the weak interaction, the gluon, and the graviton. See Allan Griffin; D. W. Snoke; S. Stringari (1996). Bose-Einstein condensation. Cambridge University Press. p. 4. ISBN 978-0-521-58990-1.
-
Richard Chace Tolman (2010). "§103: Change of H with time as a result of collisions". The principles of statistical mechanics (Reprint of 1938 Oxford University Press ed.). Dover Publications. pp. 455 ff. ISBN 978-0-486-63896-6.
...we can define a suitable quantity H to characterize the condition of a gas which a tendency to decrease with time as a result of collisions, unless the distribution of the molecules equilibrium. (p. 458)
- Paul A. Tipler (1999). "Relative intensity of reflected and transmitted light". Physics for Scientists and Engineers, Parts 1-35; Part 39 (4th ed.). Macmillan. p. 1044. ISBN 978-0-7167-3821-3.
- Massoud Kaviany (2002). "Figure 4.3(b) Radiation properties of an opaque surface". Principles of heat transfer. Wiley-IEEE. p. 381. ISBN 978-0-471-43463-4.
- BA Venkanna (2010). "§10.3.4 Absorptivity, reflectivity, and transmissivity". Fundamentals of heat and mass transfer. PHI Learning Pvt. Ltd. pp. 385–386. ISBN 978-81-203-4031-2.
- Planck 1914, p. 10
- Planck 1914, pp. 9–10, §10
- Kirchhoff 1860c
- Lummer & Kurlbaum 1898
- An extensive historical discussion is found in Mehra, Jagdish; Rechenberg, Helmut (2000). The historical development of quantum theory. Springer. pp. 39 ff. ISBN 978-0-387-95174-4.
- Kangro 1976, p. 159
- Lummer & Kurlbaum 1901
- CF Lewis (June 1988). "Materials keep a low profile" (PDF). Mech. Eng.: 37–41.
- Bradley Quinn (2010). Textile Futures. Berg. p. 68. ISBN 978-1-84520-807-3.
- ^ K. Mizuno; et al. (2009). "A black body absorber from vertically aligned single-walled carbon nanotubes". Proceedings of the National Academy of Sciences. 106 (15): 6044–6077. Bibcode:2009PNAS..106.6044M. doi:10.1073/pnas.0900155106. PMC 2669394. PMID 19339498.
- Zu-Po Yang; et al. (2008). "Experimental observation of an extremely dark material made by a low-density nanotube array". Nano Letters. 8 (2): 446–451. Bibcode:2008NanoL...8..446Y. doi:10.1021/nl072369t. PMID 18181658. S2CID 7412160.
- See description of work by Richard Brown and his colleagues at the UK's National Physical Laboratory: Mick Hamer (6 February 2003). "Mini craters key to 'blackest ever black'". New Scientist.
- Ghai, Viney; Singh, Harpreet; Agnihotri, Prabhat K. (2019). "Dandelion-Like Carbon Nanotubes for Near-Perfect Black Surfaces". ACS Applied Nano Materials. 2 (12): 7951–7956. doi:10.1021/acsanm.9b01950. S2CID 213017898.
-
Simon F. Green; Mark H. Jones; S. Jocelyn Burnell (2004). An introduction to the sun and stars. Cambridge University Press. pp. 21–22, 53. ISBN 978-0-521-54622-5.
A source in which photons are much more likely to interact with the material within the source than to escape is a condition for the formation of a black-body spectrum
- David H. Kelley; Eugene F. Milone; Anthony F. (FRW) Aveni (2011). Exploring Ancient Skies: A Survey of Ancient and Cultural Astronomy (2nd ed.). Springer. p. 52. ISBN 978-1-4419-7623-9.
- David F Gray (February 1995). "Comparing the sun with other stars along the temperature coordinate". Publications of the Astronomical Society of the Pacific. 107: 120–123. Bibcode:1995PASP..107..120G. doi:10.1086/133525.
- M Golay (1974). "Table IX: U-B Indices". Introduction to astronomical photometry. Springer. p. 82. ISBN 978-90-277-0428-3.
- Lawrence Hugh Aller (1991). Atoms, stars, and nebulae (3rd ed.). Cambridge University Press. p. 61. ISBN 978-0-521-31040-6.
- Kenneth R. Lang (2006). Astrophysical formulae, Volume 1 (3rd ed.). Birkhäuser. p. 23. ISBN 978-3-540-29692-8.
- B. Bertotti; Paolo Farinella; David Vokrouhlický (2003). "Figure 9.2: The temperature profile in the solar atmosphere". New Views of the Solar System. Springer. p. 248. ISBN 978-1-4020-1428-4.
- Figure modeled after E. Böhm-Vitense (1989). "Figure 4.9". Introduction to Stellar Astrophysics: Basic stellar observations and data. Cambridge University Press. p. 26. ISBN 978-0-521-34869-0.
- Schutz, Bernard (2004). Gravity From the Group Up: An Introductory Guide to Gravity and General Relativity (1st ed.). Cambridge University Press. p. 304. ISBN 978-0-521-45506-0.
- PCW Davies (1978). "Thermodynamics of black holes" (PDF). Rep Prog Phys. 41 (8): 1313–1355. Bibcode:1978RPPh...41.1313D. doi:10.1088/0034-4885/41/8/004. S2CID 250916407. Archived from the original (PDF) on 10 May 2013.
- Robert M Wald (2005). "The thermodynamics of black holes". In Andrés Gomberoff; Donald Marolf (eds.). Lectures on quantum gravity. Springer Science & Business Media. pp. 1–38. ISBN 978-0-387-23995-8.
- Bernard J Carr & Steven B Giddings (2008). "Chapter 6: Quantum black holes". Beyond Extreme Physics: Cutting-edge science. Rosen Publishing Group, Scientific American (COR). p. 30. ISBN 978-1-4042-1402-6.
- Valeri P. Frolov; Andrei Zelnikov (2011). "Equation 9.7.1". Introduction to Black Hole Physics. Oxford University Press. p. 321. ISBN 978-0-19-969229-3.
-
Robert M Wald (2005). "The thermodynamics of black holes (pp. 1–38)". In Andrés Gomberoff; Donald Marolf (eds.). Lectures on Quantum Gravity. Springer Science & Business Media. p. 28. ISBN 978-0-387-23995-8.
... no results on black hole thermodynamics have been subject to any experimental or observational tests ...
- White, M. (1999). "Anisotropies in the CMB" (PDF). Proceedings of the Los Angeles Meeting, DPF 99. UCLA. See also arXive.org.
- "2022 CODATA Value: Stefan–Boltzmann constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. May 2024. Retrieved 18 May 2024.
- A simple example is provided by Srivastava M. K. (2011). "Cooling by radiation". The Person Guide to Objective Physics for the IIT-JEE. Pearson Education India. p. 610. ISBN 978-81-317-5513-6.
- M Vollmer; K-P Mõllmann (2011). "Figure 1.38: Some examples for temperature dependence of emissivity for different materials". Infrared Thermal Imaging: Fundamentals, Research and Applications. John Wiley & Sons. p. 45. ISBN 978-3-527-63087-5.
- Robert Osiander; M. Ann Garrison Darrin; John Champion (2006). MEMS and Microstructures in aerospace applications. CRC Press. p. 187. ISBN 978-0-8247-2637-9.
-
Krishna Rajagopal; Frank Wilczek (2001). "6.2 Coling by Neutrino Emissions (pp. 2135-2136) – The Condensed Matter Physics of QCD". In Mikhail A. Shifman (ed.). At The Frontier of Particle Physics: Handbook of QCD (On the occasion of the 75th birthday of Professor Boris Ioffe). Vol. 3. Singapore: World Scientific. pp. 2061–2151. arXiv:hep-ph/0011333v2. CiteSeerX 10.1.1.344.2269. doi:10.1142/9789812810458_0043. ISBN 978-981-02-4969-4. S2CID 13606600.
For the first 10 years of its life, the cooling of a neutron star is governed by the balance between heat capacity and the loss of heat by neutrino emission. ... Both the specific heat CV and the neutrino emission rate Lν are dominated by physics within T of the Fermi surface. ... The star will cool rapidly until its interior temperature is T < Tc ~ ∆, at which time the quark matter core will become inert and the further cooling history will be dominated by neutrino emission from the nuclear matter fraction of the star.
- Walter Lewin; Warren Goldstein (2011). "X-ray bursters!". For the love of physics. Simon and Schuster. pp. 251 ff. ISBN 978-1-4391-0827-7.
- TE Strohmayer (2006). "Neutron star structure and fundamental physics". In John W. Mason (ed.). Astrophysics update, Volume 2. Birkhäuser. p. 41. ISBN 978-3-540-30312-1.
Bibliography
- Chandrasekhar, S. (1950). Radiative Transfer. Oxford University Press.
- Goody, R. M.; Yung, Y. L. (1989). Atmospheric Radiation: Theoretical Basis (2nd ed.). Oxford University Press. ISBN 978-0-19-510291-8.
- Hermann, A. (1971). The Genesis of Quantum Theory. Nash, C.W. (transl.). MIT Press. ISBN 978-0-262-08047-7. a translation of Frühgeschichte der Quantentheorie (1899–1913), Physik Verlag, Mosbach/Baden.
- Kangro, H. (1976). Early History of Planck's Radiation Law. Taylor and Francis. ISBN 978-0-85066-063-0.
- Kirchhoff, G. (1860a). "Über die Fraunhofer'schen Linien". Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin: 662–665.
- Kirchhoff, G. (1860b). "Über den Zusammenhang zwischen Emission und Absorption von Licht und Wärme". Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin: 783–787.
- Kirchhoff, G. (1860c). "Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme and Licht". Annalen der Physik und Chemie. 185 (2): 275–301. Bibcode:1860AnP...185..275K. doi:10.1002/andp.18601850205. Translated by Guthrie, F. as Kirchhoff, G. (1860). "On the relation between the radiating and absorbing powers of different bodies for light and heat". Philosophical Magazine. Series 4. 20: 1–21.
- Kirchhoff, G. (1882) . "Ueber das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme und Licht". Gessamelte Abhandlungen. Leipzig: Johann Ambrosius Barth. pp. 571–598.
- Kondepudi, D.; Prigogine, I. (1998). Modern Thermodynamics. From Heat Engines to Dissipative Structures. John Wiley & Sons. ISBN 978-0-471-97393-5.
- Kragh, H. (1999). Quantum Generations: a History of Physics in the Twentieth Century. Princeton University Press. ISBN 978-0-691-01206-3.
- Kuhn, T. S. (1978). Black–Body Theory and the Quantum Discontinuity. Oxford University Press. ISBN 978-0-19-502383-1.
- Loudon, R. (2000) . The Quantum Theory of Light (third ed.). Cambridge University Press. ISBN 978-0-19-850177-0.
- Lummer, O.; Kurlbaum, F. (1898). "Der electrisch geglühte "absolut schwarze" Körper und seine Temperaturmessung". Verhandlungen der Deutschen Physikalischen Gesellschaft. 17: 106–111.
- Lummer, O.; Kurlbaum, F. (1901). "Der elektrisch geglühte "schwarze" Körper". Annalen der Physik. 310 (8): 829–836. Bibcode:1901AnP...310..829L. doi:10.1002/andp.19013100809.
- Mandel, L.; Wolf, E. (1995). Optical Coherence and Quantum Optics. Cambridge University Press. ISBN 978-0-521-41711-2.
- Mehra, J.; Rechenberg, H. (1982). The Historical Development of Quantum Theory. Vol. 1, part 1. Springer-Verlag. ISBN 978-0-387-90642-3.
- Mihalas, D.; Weibel-Mihalas, B. (1984). Foundations of Radiation Hydrodynamics. Oxford University Press. ISBN 978-0-19-503437-0.
- Milne, E.A. (1930). "Thermodynamics of the Stars". Handbuch der Astrophysik. 3, part 1: 63–255.
- Planck, M. (1914). The Theory of Heat Radiation. Masius, M. (transl.) (2nd ed.). P. Blakiston's Son & Co. OL 7154661M.
- Rybicki, G. B.; Lightman, A. P. (1979). Radiative Processes in Astrophysics. John Wiley & Sons. ISBN 978-0-471-82759-7.
- Schirrmacher, A. (2001). Experimenting theory: the proofs of Kirchhoff's radiation law before and after Planck. Münchner Zentrum für Wissenschafts und Technikgeschichte.
- Stewart, B. (1858). "An account of some experiments on radiant heat". Transactions of the Royal Society of Edinburgh. 22: 1–20. doi:10.1017/S0080456800031288. S2CID 122316368.
External links
- Keesey, Lori J. (12 December 2010). "Blacker than black". NASA. Archived from the original on 14 June 2020. Retrieved 1 February 2012.
Engineers now developing a blacker-than pitch material that will help scientists gather hard-to-obtain scientific measurements... nanotech-based material now being developed by a team of 10 technologists at the NASA Goddard Space Flight Center

