Misplaced Pages

Latest revision as of 16:14, 8 December 2024

Inductor

A selection of low-value inductors
Type	Passive
Working principle‍	Electromagnetic induction
Inventor	Michael Faraday
Invention year	1831; 194 years ago (1831)
Number of terminals	2
Electronic symbol

An inductor, also called a coil, choke, or reactor, is a passive two-terminal electrical component that stores energy in a magnetic field when an electric current flows through it. An inductor typically consists of an insulated wire wound into a coil.

When the current flowing through the coil changes, the time-varying magnetic field induces an electromotive force (emf) (voltage) in the conductor, described by Faraday's law of induction. According to Lenz's law, the induced voltage has a polarity (direction) which opposes the change in current that created it. As a result, inductors oppose any changes in current through them.

An inductor is characterized by its inductance, which is the ratio of the voltage to the rate of change of current. In the International System of Units (SI), the unit of inductance is the henry (H) named for 19th century American scientist Joseph Henry. In the measurement of magnetic circuits, it is equivalent to ⁠weber/ampere⁠. Inductors have values that typically range from 1 μH (10 H) to 20 H. Many inductors have a magnetic core made of iron or ferrite inside the coil, which serves to increase the magnetic field and thus the inductance. Along with capacitors and resistors, inductors are one of the three passive linear circuit elements that make up electronic circuits. Inductors are widely used in alternating current (AC) electronic equipment, particularly in radio equipment. They are used to block AC while allowing DC to pass; inductors designed for this purpose are called chokes. They are also used in electronic filters to separate signals of different frequencies, and in combination with capacitors to make tuned circuits, used to tune radio and TV receivers.

The term inductor seems to come from Heinrich Daniel Ruhmkorff, who called the induction coil he invented in 1851 an inductorium.

Description

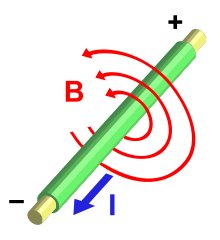
An electric current flowing through a conductor generates a magnetic field surrounding it. The magnetic flux linkage ${\displaystyle \Phi _{\mathbf {B} }}$ generated by a given current ${\displaystyle I}$ depends on the geometric shape of the circuit. Their ratio defines the inductance ${\displaystyle L}$. Thus

${\displaystyle L:={\frac {\Phi _{\mathbf {B} }}{I}}}$.

The inductance of a circuit depends on the geometry of the current path as well as the magnetic permeability of nearby materials. An inductor is a component consisting of a wire or other conductor shaped to increase the magnetic flux through the circuit, usually in the shape of a coil or helix, with two terminals. Winding the wire into a coil increases the number of times the magnetic flux lines link the circuit, increasing the field and thus the inductance. The more turns, the higher the inductance. The inductance also depends on the shape of the coil, separation of the turns, and many other factors. By adding a "magnetic core" made of a ferromagnetic material like iron inside the coil, the magnetizing field from the coil will induce magnetization in the material, increasing the magnetic flux. The high permeability of a ferromagnetic core can increase the inductance of a coil by a factor of several thousand over what it would be without it.

Constitutive equation

Any change in the current through an inductor creates a changing flux, inducing a voltage across the inductor. By Faraday's law of induction, the voltage ${\displaystyle {\mathcal {E}}}$ induced by any change in magnetic flux through the circuit is given by

${\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{\mathbf {B} }}{dt}}}$.

Reformulating the definition of L above, we obtain

${\displaystyle \Phi _{\mathbf {B} }=LI}$.

It follows that

${\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{\mathbf {B} }}{dt}}=-{\frac {d}{dt}}(LI)}$

${\displaystyle \quad {\mathcal {E}}=-L{\frac {dI}{dt}}\quad }$

if L is independent of time, current and magnetic flux linkage. Thus, inductance is also a measure of the amount of electromotive force (voltage) generated for a given rate of change of current. This is usually taken to be the constitutive relation (defining equation) of the inductor.

Lenz's law

The polarity (direction) of the induced voltage is given by Lenz's law, which states that the induced voltage will be such as to oppose the change in current. For example, if the current through an inductor is increasing, the induced potential difference will be positive at the current's entrance point and negative at the exit point, tending to oppose the additional current. The energy from the external circuit necessary to overcome this potential "hill" is being stored in the magnetic field of the inductor. If the current is decreasing, the induced voltage will be negative at the current's entrance point and positive at the exit point, tending to maintain the current. In this case energy from the magnetic field is being returned to the circuit.

Positive form of current–voltage relationship

Because the induced voltage is positive at the current's entrance terminal, the inductor's current–voltage relationship is often expressed without a negative sign by using the current's exit terminal as the reference point for the voltage ${\displaystyle V(t)}$ at the current's entrance terminal (as labeled in the schematic).

The derivative form of this current–voltage relationship is then:$${\displaystyle V(t)=L{\frac {\mathrm {d} I(t)}{\mathrm {d} t}}\,.}$$The integral form of this current–voltage relationship, starting at time ${\displaystyle t_{0}}$ with some initial current ${\displaystyle I(t_{0})}$, is then:$${\displaystyle I(t)=I(t_{0})+{\frac {1}{L}}\int _{t_{0}}^{t}V(\tau )\,\mathrm {d} \tau \,.}$$The dual of the inductor is the capacitor, which stores energy in an electric field rather than a magnetic field. Its current–voltage relation replaces L with the capacitance C and has current and voltage swapped from these equations.

Energy stored in an inductor

One intuitive explanation as to why a potential difference is induced on a change of current in an inductor goes as follows:

When there is a change in current through an inductor there is a change in the strength of the magnetic field. For example, if the current is increased, the magnetic field increases. This, however, does not come without a price. The magnetic field contains potential energy, and increasing the field strength requires more energy to be stored in the field. This energy comes from the electric current through the inductor. The increase in the magnetic potential energy of the field is provided by a corresponding drop in the electric potential energy of the charges flowing through the windings. This appears as a voltage drop across the windings as long as the current increases. Once the current is no longer increased and is held constant, the energy in the magnetic field is constant and no additional energy must be supplied, so the voltage drop across the windings disappears.

Similarly, if the current through the inductor decreases, the magnetic field strength decreases, and the energy in the magnetic field decreases. This energy is returned to the circuit in the form of an increase in the electrical potential energy of the moving charges, causing a voltage rise across the windings.

Derivation

The work done per unit charge on the charges passing through the inductor is ${\displaystyle -{\mathcal {E}}}$. The negative sign indicates that the work is done against the emf, and is not done by the emf. The current ${\displaystyle I}$ is the charge per unit time passing through the inductor. Therefore, the rate of work ${\displaystyle W}$ done by the charges against the emf, that is the rate of change of energy of the current, is given by

${\displaystyle {\frac {dW}{dt}}=-{\mathcal {E}}I}$

From the constitutive equation for the inductor, ${\displaystyle -{\mathcal {E}}=L{\frac {dI}{dt}}}$ so

${\displaystyle {\frac {dW}{dt}}=L{\frac {dI}{dt}}\cdot I=LI\cdot {\frac {dI}{dt}}}$

${\displaystyle dW=LI\cdot dI}$

In a ferromagnetic core inductor, when the magnetic field approaches the level at which the core saturates, the inductance will begin to change, it will be a function of the current ${\displaystyle L(I)}$. Neglecting losses, the energy ${\displaystyle W}$ stored by an inductor with a current ${\displaystyle I_{0}}$ passing through it is equal to the amount of work required to establish the current through the inductor.

This is given by: ${\displaystyle W=\int _{0}^{I_{0}}L_{d}(I)\,I\,dI}$, where ${\displaystyle L_{d}(I)}$ is the so-called "differential inductance" and is defined as: ${\displaystyle L_{d}={\frac {d\Phi _{\mathbf {B} }}{dI}}}$. In an air core inductor or a ferromagnetic core inductor below saturation, the inductance is constant (and equal to the differential inductance), so the stored energy is

${\displaystyle W=L\int _{0}^{I_{0}}I\,dI}$

${\displaystyle \quad W={\frac {1}{2}}L{I_{0}}^{2}\quad }$

For inductors with magnetic cores, the above equation is only valid for linear regions of the magnetic flux, at currents below the saturation level of the inductor, where the inductance is approximately constant. Where this is not the case, the integral form must be used with ${\displaystyle L_{d}}$ variable.

Voltage step response

When a voltage step is applied to an inductor:

• In the short-time limit, since the current cannot change instantaneously, the initial current is zero. The equivalent circuit of an inductor immediately after the step is applied is an open circuit.
• As time passes, the current increases at a constant rate with time until the inductor starts to saturate.
• In the long-time limit, the transient response of the inductor will die out, the magnetic flux through the inductor will become constant, so no voltage would be induced between the terminals of the inductor. Therefore, assuming the resistance of the windings is negligible, the equivalent circuit of an inductor a long time after the step is applied is a short circuit.

Ideal and real inductors

The constitutive equation describes the behavior of an ideal inductor with inductance ${\displaystyle L}$, and without resistance, capacitance, or energy dissipation. In practice, inductors do not follow this theoretical model; real inductors have a measurable resistance due to the resistance of the wire and energy losses in the core, and parasitic capacitance between turns of the wire.

A real inductor's capacitive reactance rises with frequency, and at a certain frequency, the inductor will behave as a resonant circuit. Above this self-resonant frequency, the capacitive reactance is the dominant part of the inductor's impedance. At higher frequencies, resistive losses in the windings increase due to the skin effect and proximity effect.

Inductors with ferromagnetic cores experience additional energy losses due to hysteresis and eddy currents in the core, which increase with frequency. At high currents, magnetic core inductors also show sudden departure from ideal behavior due to nonlinearity caused by magnetic saturation of the core.

Inductors radiate electromagnetic energy into surrounding space and may absorb electromagnetic emissions from other circuits, resulting in potential electromagnetic interference.

An early solid-state electrical switching and amplifying device called a saturable reactor exploits saturation of the core as a means of stopping the inductive transfer of current via the core.

Q factor

The winding resistance appears as a resistance in series with the inductor; it is referred to as DCR (DC resistance). This resistance dissipates some of the reactive energy. The quality factor (or Q) of an inductor is the ratio of its inductive reactance to its resistance at a given frequency, and is a measure of its efficiency. The higher the Q factor of the inductor, the closer it approaches the behavior of an ideal inductor. High Q inductors are used with capacitors to make resonant circuits in radio transmitters and receivers. The higher the Q is, the narrower the bandwidth of the resonant circuit.

The Q factor of an inductor is defined as

${\displaystyle Q={\frac {\omega L}{R}}}$

where ${\displaystyle L}$ is the inductance, ${\displaystyle R}$ is the DC resistance, and the product ${\displaystyle \omega L}$ is the inductive reactance

Q increases linearly with frequency if L and R are constant. Although they are constant at low frequencies, the parameters vary with frequency. For example, skin effect, proximity effect, and core losses increase R with frequency; winding capacitance and variations in permeability with frequency affect L.

At low frequencies and within limits, increasing the number of turns N improves Q because L varies as N while R varies linearly with N. Similarly increasing the radius r of an inductor improves (or increases) Q because L varies with r while R varies linearly with r. So high Q air core inductors often have large diameters and many turns. Both of those examples assume the diameter of the wire stays the same, so both examples use proportionally more wire. If the total mass of wire is held constant, then there would be no advantage to increasing the number of turns or the radius of the turns because the wire would have to be proportionally thinner.

Using a high permeability ferromagnetic core can greatly increase the inductance for the same amount of copper, so the core can also increase the Q. Cores however also introduce losses that increase with frequency. The core material is chosen for best results for the frequency band. High Q inductors must avoid saturation; one way is by using a (physically larger) air core inductor. At VHF or higher frequencies an air core is likely to be used. A well designed air core inductor may have a Q of several hundred.

Applications

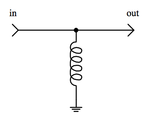
Inductors are used extensively in analog circuits and signal processing. Applications range from the use of large inductors in power supplies, which in conjunction with filter capacitors remove ripple which is a multiple of the mains frequency (or the switching frequency for switched-mode power supplies) from the direct current output, to the small inductance of the ferrite bead or torus installed around a cable to prevent radio frequency interference from being transmitted down the wire.

Inductors are used as the energy storage device in many switched-mode power supplies to produce DC current. The inductor supplies energy to the circuit to keep current flowing during the "off" switching periods and enables topographies where the output voltage is higher than the input voltage.

A tuned circuit, consisting of an inductor connected to a capacitor, acts as a resonator for oscillating current. Tuned circuits are widely used in radio frequency equipment such as radio transmitters and receivers, as narrow bandpass filters to select a single frequency from a composite signal, and in electronic oscillators to generate sinusoidal signals.

Two (or more) inductors in proximity that have coupled magnetic flux (mutual inductance) form a transformer, which is a fundamental component of every electric utility power grid. The efficiency of a transformer may decrease as the frequency increases due to eddy currents in the core material and skin effect on the windings. The size of the core can be decreased at higher frequencies. For this reason, aircraft use 400 hertz alternating current rather than the usual 50 or 60 hertz, allowing a great saving in weight from the use of smaller transformers. Transformers enable switched-mode power supplies that galvanically isolate the output from the input.

Inductors are also employed in electrical transmission systems, where they are used to limit switching currents and fault currents. In this field, they are more commonly referred to as reactors.

Inductors have parasitic effects which cause them to depart from ideal behavior. They create and suffer from electromagnetic interference (EMI). Their physical size prevents them from being integrated on semiconductor chips. So the use of inductors is declining in modern electronic devices, particularly compact portable devices. Real inductors are increasingly being replaced by active circuits such as the gyrator which can synthesize inductance using capacitors.

Inductor construction

An inductor usually consists of a coil of conducting material, typically insulated copper wire, wrapped around a core either of plastic (to create an air-core inductor) or of a ferromagnetic (or ferrimagnetic) material; the latter is called an "iron core" inductor. The high permeability of the ferromagnetic core increases the magnetic field and confines it closely to the inductor, thereby increasing the inductance. Low frequency inductors are constructed like transformers, with cores of electrical steel laminated to prevent eddy currents. 'Soft' ferrites are widely used for cores above audio frequencies, since they do not cause the large energy losses at high frequencies that ordinary iron alloys do. Inductors come in many shapes. Some inductors have an adjustable core, which enables changing of the inductance. Inductors used to block very high frequencies are sometimes made by stringing a ferrite bead on a wire.

Small inductors can be etched directly onto a printed circuit board by laying out the trace in a spiral pattern. Some such planar inductors use a planar core. Small value inductors can also be built on integrated circuits using the same processes that are used to make interconnects. Aluminium interconnect is typically used, laid out in a spiral coil pattern. However, the small dimensions limit the inductance, and it is far more common to use a circuit called a gyrator that uses a capacitor and active components to behave similarly to an inductor. Regardless of the design, because of the low inductances and low power dissipation on-die inductors allow, they are currently only commercially used for high frequency RF circuits.

Shielded inductors

Inductors used in power regulation systems, lighting, and other systems that require low-noise operating conditions, are often partially or fully shielded. In telecommunication circuits employing induction coils and repeating transformers shielding of inductors in close proximity reduces circuit cross-talk.

Types

Air-core inductor

The term air core coil describes an inductor that does not use a magnetic core made of a ferromagnetic material. The term refers to coils wound on plastic, ceramic, or other nonmagnetic forms, as well as those that have only air inside the windings. Air core coils have lower inductance than ferromagnetic core coils, but are often used at high frequencies because they are free from energy losses called core losses that occur in ferromagnetic cores, which increase with frequency. A side effect that can occur in air core coils in which the winding is not rigidly supported on a form is 'microphony': mechanical vibration of the windings can cause variations in the inductance.

Radio-frequency inductor

At high frequencies, particularly radio frequencies (RF), inductors have higher resistance and other losses. In addition to causing power loss, in resonant circuits this can reduce the Q factor of the circuit, broadening the bandwidth. In RF inductors specialized construction techniques are used to minimize these losses. The losses are due to these effects:

• Skin effect: The resistance of a wire to high frequency current is higher than its resistance to direct current because of skin effect. Due to induced eddy currents, radio frequency alternating current does not penetrate far into the body of a conductor but travels along its surface. For example, at 6 MHz the skin depth of copper wire is about 0.001 inches (25 μm); most of the current is within this depth of the surface. Therefore, in a solid wire, the interior portion of the wire may carry little current, effectively increasing its resistance.
• Proximity effect: Another similar effect that also increases the resistance of the wire at high frequencies is proximity effect, which occurs in parallel wires that lie close to each other. The individual magnetic field of adjacent turns induces eddy currents in the wire of the coil, which causes the current density in the conductor to be displaced away from the adjacent surfaces. Like skin effect, this reduces the effective cross-sectional area of the wire conducting current, increasing its resistance.
• Dielectric losses: The high frequency electric field near the conductors in a tank coil can cause the motion of polar molecules in nearby insulating materials, dissipating energy as heat. For this reason, coils used for tuned circuits may be suspended in air, supported by narrow plastic or ceramic strips rather than being wound on coil forms.
• Parasitic capacitance: The capacitance between individual wire turns of the coil, called parasitic capacitance, does not cause energy losses but can change the behavior of the coil. Each turn of the coil is at a slightly different potential, so the electric field between neighboring turns stores charge on the wire, so the coil acts as if it has a capacitor in parallel with it. At a high enough frequency this capacitance can resonate with the inductance of the coil forming a tuned circuit, causing the coil to become self-resonant.

To reduce parasitic capacitance and proximity effect, high Q RF coils are constructed to avoid having many turns lying close together, parallel to one another. The windings of RF coils are often limited to a single layer, and the turns are spaced apart. To reduce resistance due to skin effect, in high-power inductors such as those used in transmitters the windings are sometimes made of a metal strip or tubing which has a larger surface area, and the surface is silver-plated.

Basket-weave coils

To reduce proximity effect and parasitic capacitance, multilayer RF coils are wound in patterns in which successive turns are not parallel but crisscrossed at an angle; these are often called honeycomb or basket-weave coils. These are occasionally wound on a vertical insulating supports with dowels or slots, with the wire weaving in and out through the slots.

Spiderweb coils

Another construction technique with similar advantages is flat spiral coils. These are often wound on a flat insulating support with radial spokes or slots, with the wire weaving in and out through the slots; these are called spiderweb coils. The form has an odd number of slots, so successive turns of the spiral lie on opposite sides of the form, increasing separation.

Litz wire

To reduce skin effect losses, some coils are wound with a special type of radio frequency wire called litz wire. Instead of a single solid conductor, litz wire consists of a number of smaller wire strands that carry the current. Unlike ordinary stranded wire, the strands are insulated from each other, to prevent skin effect from forcing the current to the surface, and are twisted or braided together. The twist pattern ensures that each wire strand spends the same amount of its length on the outside of the wire bundle, so skin effect distributes the current equally between the strands, resulting in a larger cross-sectional conduction area than an equivalent single wire.

Axial Inductor

Small inductors for low current and low power are made in molded cases resembling resistors. These may be either plain (phenolic) core or ferrite core. An ohmmeter readily distinguishes them from similar-sized resistors by showing the low resistance of the inductor.

Ferromagnetic-core inductor

Ferromagnetic-core or iron-core inductors use a magnetic core made of a ferromagnetic or ferrimagnetic material such as iron or ferrite to increase the inductance. A magnetic core can increase the inductance of a coil by a factor of several thousand, by increasing the magnetic field due to its higher magnetic permeability. However the magnetic properties of the core material cause several side effects which alter the behavior of the inductor and require special construction:

Core losses

A time-varying current in a ferromagnetic inductor, which causes a time-varying magnetic field in its core, causes energy losses in the core material that are dissipated as heat, due to two processes:

Eddy currents

From Faraday's law of induction, the changing magnetic field can induce circulating loops of electric current in the conductive metal core. The energy in these currents is dissipated as heat in the resistance of the core material. The amount of energy lost increases with the area inside the loop of current.

Hysteresis

Changing or reversing the magnetic field in the core also causes losses due to the motion of the tiny magnetic domains it is composed of. The energy loss is proportional to the area of the hysteresis loop in the BH graph of the core material. Materials with low coercivity have narrow hysteresis loops and so low hysteresis losses.

Core loss is non-linear with respect to both frequency of magnetic fluctuation and magnetic flux density. Frequency of magnetic fluctuation is the frequency of AC current in the electric circuit; magnetic flux density corresponds to current in the electric circuit. Magnetic fluctuation gives rise to hysteresis, and magnetic flux density causes eddy currents in the core. These nonlinearities are distinguished from the threshold nonlinearity of saturation. Core loss can be approximately modeled with Steinmetz's equation. At low frequencies and over limited frequency spans (maybe a factor of 10), core loss may be treated as a linear function of frequency with minimal error. However, even in the audio range, nonlinear effects of magnetic core inductors are noticeable and of concern.

Saturation

If the current through a magnetic core coil is high enough that the core saturates, the inductance will fall and current will rise dramatically. This is a nonlinear threshold phenomenon and results in distortion of the signal. For example, audio signals can suffer intermodulation distortion in saturated inductors. To prevent this, in linear circuits the current through iron core inductors must be limited below the saturation level. Some laminated cores have a narrow air gap in them for this purpose, and powdered iron cores have a distributed air gap. This allows higher levels of magnetic flux and thus higher currents through the inductor before it saturates.

Curie point demagnetization

If the temperature of a ferromagnetic or ferrimagnetic core rises to a specified level, the magnetic domains dissociate, and the material becomes paramagnetic, no longer able to support magnetic flux. The inductance falls and current rises dramatically, similarly to what happens during saturation. The effect is reversible: When the temperature falls below the Curie point, magnetic flux resulting from current in the electric circuit will realign the magnetic domains of the core and its magnetic flux will be restored. The Curie point of ferromagnetic materials (iron alloys) is quite high; iron is highest at 770 °C. However, for some ferrimagnetic materials (ceramic iron compounds – ferrites) the Curie point can be close to ambient temperatures (below 100 °C).

Laminated-core inductor

Low-frequency inductors are often made with laminated cores to prevent eddy currents, using construction similar to transformers. The core is made of stacks of thin steel sheets or laminations oriented parallel to the field, with an insulating coating on the surface. The insulation prevents eddy currents between the sheets, so any remaining currents must be within the cross sectional area of the individual laminations, reducing the area of the loop and thus reducing the energy losses greatly. The laminations are made of low-conductivity silicon steel to further reduce eddy current losses.

Ferrite-core inductor

For higher frequencies, inductors are made with cores of ferrite. Ferrite is a ceramic ferrimagnetic material that is nonconductive, so eddy currents cannot flow within it. The formulation of ferrite is xxFe₂O₄ where xx represents various metals. For inductor cores soft ferrites are used, which have low coercivity and thus low hysteresis losses.

Powdered-iron-core inductor

Another material is powdered iron cemented with a binder. Medium frequency equipment almost exclusively uses powdered iron cores, and inductors and transformers built for the lower shortwaves are made using either cemented powdered iron or ferrites.

Toroidal-core inductor

In an inductor wound on a straight rod-shaped core, the magnetic field lines emerging from one end of the core must pass through the air to re-enter the core at the other end. This reduces the field, because much of the magnetic field path is in air rather than the higher permeability core material and is a source of electromagnetic interference. A higher magnetic field and inductance can be achieved by forming the core in a closed magnetic circuit. The magnetic field lines form closed loops within the core without leaving the core material. The shape often used is a toroidal or doughnut-shaped ferrite core. Because of their symmetry, toroidal cores allow a minimum of the magnetic flux to escape outside the core (called leakage flux), so they radiate less electromagnetic interference than other shapes. Toroidal core coils are manufactured of various materials, primarily ferrite, powdered iron and laminated cores.

Variable inductor

Probably the most common type of variable inductor today is one with a moveable ferrite magnetic core, which can be slid or screwed in or out of the coil. Moving the core farther into the coil increases the permeability, increasing the magnetic field and the inductance. Many inductors used in radio applications (usually less than 100 MHz) use adjustable cores in order to tune such inductors to their desired value, since manufacturing processes have certain tolerances (inaccuracy). Sometimes such cores for frequencies above 100 MHz are made from highly conductive non-magnetic material such as aluminum. They decrease the inductance because the magnetic field must bypass them.

Air core inductors can use sliding contacts or multiple taps to increase or decrease the number of turns included in the circuit, to change the inductance. A type much used in the past but mostly obsolete today has a spring contact that can slide along the bare surface of the windings. The disadvantage of this type is that the contact usually short-circuits one or more turns. These turns act like a single-turn short-circuited transformer secondary winding; the large currents induced in them cause power losses.

A type of continuously variable air core inductor is the variometer. This consists of two coils with the same number of turns connected in series, one inside the other. The inner coil is mounted on a shaft so its axis can be turned with respect to the outer coil. When the two coils' axes are collinear, with the magnetic fields pointing in the same direction, the fields add and the inductance is maximum. When the inner coil is turned so its axis is at an angle with the outer, the mutual inductance between them is smaller so the total inductance is less. When the inner coil is turned 180° so the coils are collinear with their magnetic fields opposing, the two fields cancel each other and the inductance is very small. This type has the advantage that it is continuously variable over a wide range. It is used in antenna tuners and matching circuits to match low frequency transmitters to their antennas.

Another method to control the inductance without any moving parts requires an additional DC current bias winding which controls the permeability of an easily saturable core material. See Magnetic amplifier.

Choke

A choke is an inductor designed specifically for blocking high-frequency alternating current (AC) in an electrical circuit, while allowing DC or low-frequency signals to pass. Because the inductor restricts or "chokes" the changes in current, this type of inductor is called a choke. It usually consists of a coil of insulated wire wound on a magnetic core, although some consist of a donut-shaped "bead" of ferrite material strung on a wire. Like other inductors, chokes resist changes in current passing through them increasingly with frequency. The difference between chokes and other inductors is that chokes do not require the high Q factor construction techniques that are used to reduce the resistance in inductors used in tuned circuits.

Circuit analysis

The effect of an inductor in a circuit is to oppose changes in current through it by developing a voltage across it proportional to the rate of change of the current. An ideal inductor would offer no resistance to a constant direct current; however, only superconducting inductors have truly zero electrical resistance.

The relationship between the time-varying voltage v(t) across an inductor with inductance L and the time-varying current i(t) passing through it is described by the differential equation:

${\displaystyle v(t)=L{\frac {di(t)}{dt}}}$

When there is a sinusoidal alternating current (AC) through an inductor, a sinusoidal voltage is induced. The amplitude of the voltage is proportional to the product of the amplitude (${\displaystyle I_{P}}$) of the current and the angular frequency (${\displaystyle \omega }$) of the current.

${\displaystyle {\begin{aligned}i(t)&=I_{\mathrm {P} }\sin(\omega t)\\{\frac {di(t)}{dt}}&=I_{\mathrm {P} }\omega \cos(\omega t)\\v(t)&=LI_{\mathrm {P} }\omega \cos(\omega t)\end{aligned}}}$

In this situation, the phase of the current lags that of the voltage by π/2 (90°). For sinusoids, as the voltage across the inductor goes to its maximum value, the current goes to zero, and as the voltage across the inductor goes to zero, the current through it goes to its maximum value.

If an inductor is connected to a direct current source with value I via a resistance R (at least the DCR of the inductor), and then the current source is short-circuited, the differential relationship above shows that the current through the inductor will discharge with an exponential decay:

${\displaystyle i(t)=Ie^{-{\frac {R}{L}}t}}$

Reactance

The ratio of the peak voltage to the peak current in an inductor energised from an AC source is called the reactance and is denoted X_L.

${\displaystyle X_{\mathrm {L} }={\frac {V_{\mathrm {P} }}{I_{\mathrm {P} }}}={\frac {\omega LI_{\mathrm {P} }}{I_{\mathrm {P} }}}}$

Thus,

${\displaystyle X_{\mathrm {L} }=\omega L}$

where ω is the angular frequency.

Reactance is measured in ohms but referred to as impedance rather than resistance; energy is stored in the magnetic field as current rises and discharged as current falls. Inductive reactance is proportional to frequency. At low frequency the reactance falls; at DC, the inductor behaves as a short circuit. As frequency increases the reactance increases and at a sufficiently high frequency the reactance approaches that of an open circuit.

Corner frequency

In filtering applications, with respect to a particular load impedance, an inductor has a corner frequency defined as:

${\displaystyle f_{\mathrm {3\,dB} }={\frac {R}{2\pi L}}}$

Laplace circuit analysis (s-domain)

When using the Laplace transform in circuit analysis, the impedance of an ideal inductor with no initial current is represented in the s domain by:

${\displaystyle Z(s)=Ls\,}$

where

${\displaystyle L}$ is the inductance, and

${\displaystyle s}$ is the complex frequency.

If the inductor does have initial current, it can be represented by:

• adding a voltage source in series with the inductor, having the value:

  ${\displaystyle LI_{0}\,}$

  where

  ${\displaystyle L}$ is the inductance, and

  ${\displaystyle I_{0}}$ is the initial current in the inductor.

  (The source should have a polarity that is aligned with the initial current.)
• or by adding a current source in parallel with the inductor, having the value:

  ${\displaystyle {\frac {I_{0}}{s}}}$

  where

  ${\displaystyle I_{0}}$ is the initial current in the inductor.

  ${\displaystyle s}$ is the complex frequency.

Inductor networks

Inductors in a parallel configuration each have the same potential difference (voltage). To find their total equivalent inductance (L_eq):

${\displaystyle L_{\mathrm {eq} }=\left(\sum _{i=1}^{n}{1 \over L_{i}}\right)^{-1}=\left({1 \over L_{1}}+{1 \over L_{2}}+\dots +{1 \over L_{n}}\right)^{-1}.}$

The current through inductors in series stays the same, but the voltage across each inductor can be different. The sum of the potential differences (voltage) is equal to the total voltage. To find their total inductance:

${\displaystyle L_{\mathrm {eq} }=\sum _{i=1}^{n}L_{i}=L_{1}+L_{2}+\cdots +L_{n}.\,\!}$

These simple relationships hold true only when there is no mutual coupling of magnetic fields between individual inductors.

Mutual inductance

Mutual inductance occurs when the magnetic field of an inductor induces a magnetic field in an adjacent inductor. Mutual induction is the basis of transformer construction.

${\displaystyle M={\sqrt {L_{1}L_{2}}}}$

where M is the maximum mutual inductance possible between 2 inductors and L₁ and L₂ are the two inductors. In general

${\displaystyle M\leq {\sqrt {L_{1}L_{2}}}}$

as only a fraction of self flux is linked with the other. This fraction is called "Coefficient of flux linkage (K)" or "Coefficient of coupling".

${\displaystyle M=K{\sqrt {L_{1}L_{2}}}}$

Inductance formulas

The table below lists some common simplified formulas for calculating the approximate inductance of several inductor constructions.

Construction	Formula	Notes
Cylindrical air-core coil	${\displaystyle L=\mu _{0}KN^{2}{\frac {A}{\ell }}}$ L = inductance in henries (H) μ0 = permeability of free space = 4${\displaystyle \pi }$ × 10 H/m K = Nagaoka coefficient N = number of turns A = area of cross-section of the coil in square metres (m) ℓ = length of coil in metres (m)	${\displaystyle K\approx 1}$ Calculation of Nagaoka's coefficient (K) is complicated; normally it must be looked up from a table.
Straight wire conductor	${\displaystyle L={\frac {\mu _{0}}{2\pi }}\ \ell \left(A\;-\;B\right)+C}$, where: ${\displaystyle {\begin{aligned}A&=\ln \left({\frac {\ell }{r}}+{\sqrt {\left({\frac {\ell }{r}}\right)^{2}+1}}\right)\\B&={\frac {1}{{\frac {r}{\ell }}+{\sqrt {1+\left({\frac {r}{\ell }}\right)^{2}}}}}\\C&={\text{Im}}\left({\frac {n\rho J_{0}(nr)}{2\pi \omega \mu rJ_{1}(nr)}}\right)\end{aligned}}}$ L = inductance ℓ = cylinder length r = cylinder radius μ0 = permeability of free space = 4${\displaystyle \pi }$ × 10 H/m μ = conductor permeability ρ = resistivity ω = angular frequency ${\displaystyle n={\sqrt {-i{\frac {\omega \mu }{\rho }}}}=(-1+i){\sqrt {\frac {\omega \mu }{2\rho }}}}$ ${\displaystyle J_{0},J_{1}}$ are Bessel functions. ${\displaystyle {\tfrac {\mu _{0}}{2\pi }}}$ = 0.2 μH/m, exactly.	The term C gives the internal inductance of the wire with skin-effect correction (the imaginary part of the internal impedance of the wire). If ω = 0 (DC) then ${\displaystyle C={\frac {\mu }{8\pi }},}$ and as ω approaches ∞, C approaches 0. The term B subtracts rather than adds.
	${\displaystyle L={\frac {\mu _{0}}{2\pi }}\ \ell \left}$ (when d² f ≫ 1 mm² MHz) ${\displaystyle L={\frac {\mu _{0}}{2\pi }}\ \ell \left}$ (when d² f ≪ 1 mm² MHz) L = inductance (nH) ℓ = length of conductor (mm) d = diameter of conductor (mm) f = frequency ${\displaystyle {\tfrac {\mu _{0}}{2\pi }}}$ = 0.2 μH/m, exactly.	Requires ℓ > 100 d For relative permeability μr = 1 (e.g., Cu or Al).
Small loop or very short coil	${\displaystyle L\approx {\frac {\mu _{0}}{2\pi }}N^{2}\pi D\left+{\sqrt {\frac {\mu _{0}}{2\pi }}}\;{\frac {ND}{d}}{\sqrt {\frac {\mu _{\text{r}}}{2f\sigma }}}}$ L = inductance in the same units as μ0. D = Diameter of the coil (conductor center-to-center) d = diameter of the conductor N = number of turns f = operating frequency (regular f, not ω) σ = specific conductivity of the coil conductor μr = relative permeability of the conductor Total conductor length ${\displaystyle \ell _{\text{c}}\approx N\pi D}$ should be roughly 1⁄10 wavelength or smaller. Proximity effects are not included: edge-to-edge gap between turns should be 2×d or larger. ${\displaystyle {\tfrac {\mu _{0}}{2\pi }}}$ = 0.2 μH/m, exactly.	Conductor μr should be as close to 1 as possible – copper or aluminum rather than a magnetic or paramagnetic metal.
Medium or long air-core cylindrical coil	${\displaystyle L={\frac {r^{2}N^{2}}{23r+25\ell }}}$ L = inductance (μH) r = outer radius of coil (cm) ℓ = length of coil (cm) N = number of turns	Requires cylinder length ℓ > 0.4 r: Length must be at least 1⁄5 of the diameter. Not applicable to single-loop antennas or very short, stubby coils.
Multilayer air-core coil	${\displaystyle L={\frac {r^{2}N^{2}}{19r+29\ell +32d}}}$ L = inductance (μH) r = mean radius of coil (cm) ℓ = physical length of coil winding (cm) N = number of turns d = depth of coil (outer radius minus inner radius) (cm)
Flat spiral air-core coil	${\displaystyle L={\frac {r^{2}N^{2}}{20r+28d}}}$ L = inductance (μH) r = mean radius of coil (cm) N = number of turns d = depth of coil (outer radius minus inner radius) (cm)
	${\displaystyle L={\frac {r^{2}N^{2}}{8r+11d}}}$ L = inductance (μH) r = mean radius of coil (in) N = number of turns d = depth of coil (outer radius minus inner radius) (in)	Accurate to within 5 percent for d > 0.2 r.
Toroidal air-core (circular cross-section)	${\displaystyle L=2\pi N^{2}\left(D-{\sqrt {D^{2}-d^{2}}}\right)}$ L = inductance (nH) d = diameter of coil winding (cm) N = number of turns D = 2 * radius of revolution (cm)
	${\displaystyle L\approx \pi {d^{2}N^{2} \over D}}$ L = inductance (nH) d = diameter of coil winding (cm) N = number of turns D = 2 * radius of revolution (cm)	Approximation when d < 0.1 D
Toroidal air-core (rectangular cross-section)	${\displaystyle L=2N^{2}h\ln \left({\frac {d_{2}}{d_{1}}}\right)}$ L = inductance (nH) d1 = inside diameter of toroid (cm) d2 = outside diameter of toroid (cm) N = number of turns h = height of toroid (cm)

See also

• Bellini–Tosi direction finder (radio goniometer)
• Hanna curve
• Induction coil
• Induction cooking
• Induction loop
• LC circuit
• RLC circuit
• Saturable reactor – a type of adjustable inductor
• Solenoid
• Accumulator (energy)

Notes

1. Nagaoka's coefficient (K) is approximately 1 for a coil which is much longer than its diameter and is tightly wound using small gauge wire (so that it approximates a current sheet).

References

1. Alexander, Charles K.; Sadiku, Matthew N. O. (2013). Fundamentals of Electric Circuits (5 ed.). McGraw-Hill. p. 226. ISBN 978-0-07-338057-5.
2. Urbanitzky, Alfred Ritter von (1886). Electricity in the Service of Man. Macmillan and Company. p. 195.
3. Singh, Yaduvir (2011). Electro Magnetic Field Theory. Pearson India. p. 65. ISBN 978-8131760611.
4. Wadhwa, C. L. (2005). Electrical Power Systems. New Age International. p. 18. ISBN 978-8122417227.
5. Pelcovits, Robert A.; Josh Farkas (2007). Barron's AP Physics C. Barron's Educational Series. p. 646. ISBN 978-0764137105.
6. ^ Purcell, Edward M.; David J. Morin (2013). Electricity and Magnetism. Cambridge Univ. Press. p. 364. ISBN 978-1107014022.
7. Shamos, Morris H. (2012-10-16). Great Experiments in Physics: Firsthand Accounts from Galileo to Einstein. Courier Corporation. ISBN 9780486139623.
8. Schmitt, Ron (2002). Electromagnetics Explained: A Handbook for Wireless/ RF, EMC, and High-Speed Electronics. Elsevier. pp. 75–77. ISBN 978-0080505237.
9. Jaffe, Robert L.; Taylor, Washington (2018). The Physics of Energy. Cambridge Univ. Press. p. 51. ISBN 978-1108547895.
10. Lerner, Lawrence S. (1997). Physics for Scientists and Engineers, Vol. 2. Jones and Bartlet Learning. p. 856. ISBN 978-0763704605.
11. Bowick, Christopher (2011). RF Circuit Design, 2nd Ed. Newnes. pp. 7–8. ISBN 978-0080553429.
12. Kaiser, Kenneth L. (2004). Electromagnetic Compatibility Handbook. CRC Press. pp. 6.4 – 6.5. ISBN 978-0849320873.
13. "What is an inductor? What is the definition of an inductor? Overview of inductor characteristics, parameters, and types". GOTREND Technology. Retrieved 2010-09-24.
14. Ott, Henry W. (2011). Electromagnetic Compatibility Engineering. John Wiley and Sons. p. 203. ISBN 978-1118210659.
15. Violette, Norman (2013). Electromagnetic Compatibility Handbook. Springer. pp. 515–516. ISBN 978-9401771443.
16. "An Unassuming Antenna – The Ferrite Loopstick". Radio Time Traveller. January 23, 2011. Retrieved March 5, 2014.
17. Frost, Phil (December 23, 2013). "What's an appropriate core material for a loopstick antenna?". Amateur Radio beta. Stack Exchange, Inc. Retrieved March 5, 2014.
18. Poisel, Richard (2011). Antenna Systems and Electronic Warfare Applications. Artech House. p. 280. ISBN 978-1608074846.
19. Yadava, R. L. (2011). Antenna and Wave Propagation. PHI Learning Pvt. Ltd. p. 261. ISBN 978-8120342910.
20. Zurek, Stan (2023). "Skin effect". Encyclopedia Magnetica website. Retrieved 21 May 2024.
21. ^ Kazimierczuk, Marian K. (2011). High-Frequency Magnetic Components. John Wiley and Sons. ISBN 978-1-119-96491-9.
22. Zurek, Stan (2023). "Proximity effect". Encyclopedia Magnetica website. Retrieved 21 May 2024.
23. "Inductors 101" (PDF). vishay. Retrieved 2010-09-24.
24. "Inductor and Magnetic Product Terminology" (PDF). Vishay Dale. Retrieved 2012-09-24.
25. "page with aluminum cores" (PDF). Coilcraft catalog. Retrieved 10 July 2015.
26. ^ Nagaoka, Hantaro (1909-05-06). "The Inductance Coefficients of Solenoids" (PDF). Journal of the College of Science, Imperial University, Tokyo, Japan. 27: 18. Retrieved 2011-11-10.
27. Kenneth L. Kaiser, Electromagnetic Compatibility Handbook, p. 30.64, CRC Press, 2004 ISBN 0849320879.
28. Rosa, Edward B. (1908). "The Self and Mutual Inductances of Linear Conductors" (PDF). Bulletin of the Bureau of Standards. 4 (2): 301–344. doi:10.6028/bulletin.088.
29. Skilling, Hugh Hildreth (1951). Electric transmission lines : distributed constants, theory, and application. Mcgraw-Hill. pp. 153–159.
30. Rosa 1908, equation (11a), subst. radius ρ = d/2 and cgs units
31. Terman 1943, pp. 48–49, convert to natural logarithms and inches to mm.
32. Terman (1943, p. 48) states for ℓ < 100 d, include d/2ℓ within the parentheses.
33. Burger, O. & Dvorský, M. (2015). Magnetic Loop Antenna. Ostrava, Czech Republic: EDUCA TV o.p.s.
34. Values of ${\displaystyle \pi D}$ up to 1⁄3 wavelength are feasible antennas, but for windings that long, this formula will be inaccurate.
35. ARRL Handbook, 66th Ed. American Radio Relay League (1989).
36. "Helical coil calculator". Kaizer Power Electronics. 2014-07-09. Retrieved 2020-12-29.
37. Wheeler, H.A. (October 1928). "Simple Inductance Formulas for Radio Coils". Proceedings of the Institute of Radio Engineers. 16 (10): 1398. doi:10.1109/JRPROC.1928.221309. S2CID 51638679.
38. For the second formula, Terman (1943, p. 58) which cites to Wheeler 1928.
39. "A Magnetic Elevator for Neutral Atoms into a 2D State-dependent Optical Lattice Experiment". Uni-Bonn. Retrieved 2017-08-15.
40. "Spiral coil calculator". Kaizer Power Electronics. 2014-07-10. Retrieved 2020-12-29.
41. ^ Terman 1943, p. 58
42. Terman 1943, p. 57

Source

• Terman, Frederick (1943). Radio Engineers' Handbook. McGraw-Hill.

External links

• Electromagnetic components
• Energy storage
• English inventions