| Revision as of 16:33, 7 March 2006 editDoug Pardee (talk | contribs)115 edits Clarification of the two meanings; added acceptable sharpness section← Previous edit | Latest revision as of 12:40, 29 November 2024 edit undoCitation bot (talk | contribs)Bots5,436,714 edits Added publisher. Removed parameters. | Use this bot. Report bugs. | Suggested by Abductive | Category:Science of photography | #UCB_Category 32/96 | ||
| (146 intermediate revisions by 88 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Distance beyond which all objects can be brought into an acceptable focus}} | |||
| '''Hyperfocal distance''' is a distance used in ] and ]. The precise value is slightly different between the two disciplines. | |||
| ] | |||
| ] 28mm {{f/|2.8}} lens with markings for the depth of field. The lens is set at the hyperfocal distance for {{f/|22}}. The orange mark corresponding to {{f/|22}} is at the infinity mark ({{math|∞}}). Focus is acceptable from under {{val|0.7|u=m}} to infinity.]] | |||
| ] 100–300 mm zoom lens. The depth of field, and thus hyperfocal distance, changes with the focal length as well as the f-stop. This lens is set to the hyperfocal distance for {{f/|32}} at a focal length of {{val|100|u=mm}}.]] | |||
| In ] and ], '''hyperfocal distance''' is a distance from a lens beyond which all objects can be brought into an "acceptable" ]. As the hyperfocal distance is the focus distance giving the maximum ], it is the most desirable distance to set the focus of a ].<ref name="Kingslake1951">{{cite book|title=Lenses in Photography: The Practical Guide to Optics for Photographers|last=Kingslake|first=Rudolf|publisher=Garden City Press|year=1951|location=Garden City, NY}}</ref> The hyperfocal distance is entirely dependent upon what level of sharpness is considered to be acceptable. | |||
| In optics, when a ] is focused at infinity, objects at the hyperfocal distance and beyond are acceptably sharp. | |||
| The hyperfocal distance has a property called "consecutive depths of field", where a lens focused at an object whose distance from the lens is at the hyperfocal distance {{mvar|H}} will hold a depth of field from {{math|''H''/2}} to infinity, if the lens is focused to {{math|''H''/2}}, the depth of field will be from {{math|''H''/3}} to {{mvar|H}}; if the lens is then focused to {{math|''H''/3}}, the depth of field will be from {{math|''H''/4}} to {{math|''H''/2}}, etc. | |||
| ] and George Dawson first wrote about hyperfocal distance (or "focal range") in 1867.<ref name=":0">{{cite book |first1=Thomas |last1=Sutton |first2=George |last2=Dawson |title=A Dictionary of Photography |url=https://archive.org/details/dictionaryofphot00sutt |location=London |publisher=Sampson Low, Son & Marston |year=1867 }}</ref> Louis Derr in 1906 may have been the first to derive a formula for hyperfocal distance. ] wrote in 1951 about the two methods of measuring hyperfocal distance. | |||
| The distinction between the two meanings is rarely made; context is usually used to determine which meaning is intended. Since no accepted terminology exists for distinguishing between the two meanings, this article invents the terms "optical" and "photographic" hyperfocal distance. The modifiers are shown in quotes to emphasize that the terms are invented and not generally accepted. | |||
| Some cameras have their hyperfocal distance marked on the focus dial. For example, on the ] LX focusing dial there is a red dot between {{val|2|u=m}} and infinity; when the lens is set at the red dot, that is, focused at the hyperfocal distance, the depth of field stretches from {{val|2|u=m}} to infinity. Some lenses have markings indicating the hyperfocal range for specific ]s, also called a ''depth-of-field scale''.<ref>{{Cite book |last=Minolta |url=http://archive.org/details/md_zoom_images |title=Minolta MD Zoom Lenses owner's manual |year=1985 |pages=9}}</ref> | |||
| The "photographic" hyperfocal distance is slightly greater than the "optical" hyperfocal distance. The difference between the two is the same as the focal length of the lens. | |||
| == Two methods == | |||
| ==Acceptable Sharpness== | |||
| There are two common methods of defining and measuring ''hyperfocal distance'', leading to values that differ only slightly. The distinction between the two meanings is rarely made, since they have almost identical values. The value computed according to the first definition exceeds that from the second by just one ]. | |||
| ; Definition 1 | |||
| The hyperfocal distances are entirely dependent upon what level of sharpness is considered to be acceptable. The criterion for the desired acceptable sharpness is specified through the ]. The circle of confusion is the largest acceptable spot size that an infinitesimal point is to spread out to on the imaging medium (film, digital sensor, etc.). | |||
| : The hyperfocal distance is the closest distance at which a ] can be focused while keeping ] acceptably sharp. When the lens is focused at this distance, all objects at distances from half of the hyperfocal distance out to infinity will be acceptably sharp. | |||
| ; Definition 2 | |||
| : The hyperfocal distance is the distance beyond which all objects are acceptably sharp, for a lens focused at infinity. | |||
| ==Acceptable sharpness== | |||
| ==Formulae== | |||
| The hyperfocal distance is entirely dependent upon what level of sharpness is considered to be acceptable. The criterion for the desired acceptable sharpness is specified through the ] (CoC) diameter limit. This criterion is the largest acceptable spot size diameter that an infinitesimal point is allowed to spread out to on the imaging medium (film, digital sensor, etc.). | |||
| ==Formula== | |||
| The "optical" hyperfocal distance is the product of the square of the ] divided by both the ] and the ] limit chosen. | |||
| For the first definition, | |||
| <math display="block">H = \frac{f^2}{N c} + f</math> | |||
| where |
where | ||
| * {{mvar|H}} is the hyperfocal distance; | |||
| * {{mvar|f}} is the ] of the lens; | |||
| * {{mvar|N}} is ] ({{mvar|f/D}} for aperture diameter {{mvar|D}}); and | |||
| * {{mvar|c}} is the ] limit. | |||
| For any practical f-number, the added focal length is insignificant in comparison with the first term, so that | |||
| :''F'' is focal length | |||
| <math display="block">H \approx \frac{f^2}{N c}\,.</math> | |||
| :''f'' is f-stop | |||
| This formula is exact for the second definition, if {{mvar|H}} is measured from a thin lens, or from the front principal plane of a complex lens; it is also exact for the first definition if {{mvar|H}} is measured from a point that is one focal length in front of the front principal plane. For practical purposes, there is little difference between the first and second definitions. | |||
| :''Cc'' is the circle of confusion limit | |||
| ===Derivation using geometric optics=== | |||
| The "photographic" hyperfocal distance is: | |||
| ] | |||
| The following derivations refer to the accompanying figures. For clarity, half the aperture and circle of confusion are indicated.<ref>{{cite book|title=Optics in Photography - Google Books|isbn = 9780819407634|url=https://books.google.com/books?id=hcq_40I_7egC|access-date=24 September 2014|last1 = Kingslake|first1 = Rudolf|year = 1992| publisher=SPIE Press }}</ref> | |||
| :<math>D = H+F \,</math> | |||
| ====Definition 1==== | |||
| where | |||
| An object at distance {{mvar|H}} forms a sharp image at distance {{mvar|x}} (blue line). Here, objects at infinity have images with a circle of confusion indicated by the brown ellipse where the upper red ray through the focal point intersects the blue line. | |||
| First using similar triangles hatched in green, | |||
| :''D'' is "photographic" hyperfocal distance | |||
| <math display="block">\begin{array}{crcl} | |||
| & \dfrac{x-f}{c/2} & = & \dfrac{f}{D/2} \\ | |||
| \therefore & x-f & = & \dfrac{cf}{D} \\ | |||
| \therefore & x & = & f+\dfrac{cf}{D} | |||
| \end{array}</math> | |||
| Then using similar triangles dotted in purple, | |||
| :''H'' is "optical" hyperfocal distance computed as above | |||
| <math display="block">\begin{array}{crclcl} | |||
| & \dfrac{H}{D/2} & = & \dfrac{x}{c/2} \\ | |||
| \therefore & H & = & \dfrac{Dx}{c} & = & \dfrac{D}{c}\Big(f+\dfrac{cf}{D}\Big) \\ | |||
| & & = & \dfrac{Df}{c}+f & = & \dfrac{f^2}{Nc}+f | |||
| \end{array}</math> | |||
| as found above. | |||
| :''F'' is focal length | |||
| ====Definition 2==== | |||
| ==Examples== | |||
| Objects at infinity form sharp images at the focal length {{mvar|f}} (blue line). Here, an object at {{mvar|H}} forms an image with a circle of confusion indicated by the brown ellipse where the lower red ray converging to its sharp image intersects the blue line. | |||
| Using similar triangles shaded in yellow, | |||
| As an example, let's compute the hyperfocal distances for a 50 mm lens at f/16 using a circle of confusion of 0.02 mm (which might be acceptable for some amount of enlargement). In the formula above, we make F = 50 mm, f = 16, and Cc = 0.02 mm; then we compute H: | |||
| <math display="block">\begin{array}{crclcl} | |||
| & \dfrac{H}{D/2} & = & \dfrac{f}{c/2} \\ | |||
| \therefore & H & = & \dfrac{Df}{c} & = & \dfrac{f^2}{Nc} | |||
| \end{array}</math> | |||
| ==Example== | |||
| :<math>H = \frac{(50 \mbox{ mm})^2}{(16)(0.02 \mbox{ mm})}</math> | |||
| {{Image frame|content=<timeline> | |||
| ImageSize = width:512 height:512 | |||
| PlotArea = left:88 right:0 top:0 bottom:20 | |||
| Period = from:0 till:13799 | |||
| TimeAxis = orientation:horizontal | |||
| AlignBars = late | |||
| Colors = | |||
| id:grid_major value:gray(0.5) | |||
| id:grid_minor value:gray(0.8) | |||
| ScaleMajor = unit:year increment:2000 start:0 gridcolor:grid_major | |||
| ScaleMinor = unit:year increment:500 start:0 gridcolor:grid_minor | |||
| BarData = | |||
| bar:title0 text:] | |||
| bar:data00 text:focus at infinity | |||
| bar:data10 text:focus at H₁ | |||
| bar:data20 text:focus at H₁/2 | |||
| bar:data30 text:focus at H₁/3 | |||
| bar:data40 text:focus at H₁/4 | |||
| bar:title1 text:] | |||
| bar:data01 text:focus at infinity | |||
| bar:data11 text:focus at H₂ | |||
| bar:data21 text:focus at H₂/2 | |||
| bar:data31 text:focus at H₂/3 | |||
| bar:data41 text:focus at H₁/4 | |||
| bar:title2 text:] | |||
| bar:data02 text:focus at infinity | |||
| bar:data12 text:focus at H₃ | |||
| bar:data22 text:focus at H₃/2 | |||
| bar:data32 text:focus at H₃/3 | |||
| bar:data42 text:focus at H₁/4 | |||
| PlotData = | |||
| fontsize:M | |||
| bar:data00 from:10417 till:end color:pink | |||
| bar:data00 at:13500 text:∞ | |||
| bar:data00 at:10467 text:\nH₁−f₁=10417 mm | |||
| bar:data10 from:5233 till:end color:pink | |||
| bar:data10 at:13500 text:\n∞ | |||
| bar:data10 at:10467 text:H₁ = 10467 mm mark:(line,white) | |||
| bar:data10 at:5233 text:\nH₁/2 | |||
| bar:data20 from:3489 till:10467 color:pink | |||
| bar:data20 at:10467 text:\nH₁ | |||
| bar:data20 at:5233 text:H₁/2 mark:(line,white) | |||
| bar:data20 at:3489 text:\nH₁/3 | |||
| bar:data30 from:2617 till:5233 color:pink | |||
| bar:data30 at:5233 text:\nH₁/2 | |||
| bar:data30 at:3489 text:H₁/3 mark:(line,white) | |||
| bar:data30 at:2617 text:\nH₁/4 | |||
| bar:data40 from:2093 till:3489 color:coral | |||
| bar:data40 at:3489 text:\nH₁/3 | |||
| bar:data40 at:2617 text:H₁/4 mark:(line,white) | |||
| bar:data40 at:2093 text:\nH₁/5 | |||
| bar:data01 from:5208 till:end color:limegreen | |||
| :<math>H = \frac{(50 \mbox{ mm})(50 \mbox{ mm})}{(16)(0.02 \mbox{ mm})}</math> | |||
| bar:data01 at:13500 text:∞ | |||
| bar:data01 at:5258 text:\nH₂ − f₂ = 5208 mm | |||
| bar:data11 from:2629 till:end color:limegreen | |||
| bar:data11 at:13500 text:\n∞ | |||
| bar:data11 at:5258 text:H₂ = 5258 mm mark:(line,white) | |||
| bar:data11 at:2629 text:\nH₂/2 | |||
| bar:data21 from:1753 till:5258 color:yellowgreen | |||
| bar:data21 at:5258 text:\nH₂ | |||
| bar:data21 at:2629 text:H₂/2 mark:(line,white) | |||
| bar:data21 at:1753 text:\nH₂/3 | |||
| bar:data31 from:1315 till:2629 color:limegreen | |||
| bar:data31 at:2629 text:\nH₂/2 | |||
| bar:data31 at:1753 text:H₂/3 mark:(line,white) | |||
| bar:data31 at:1315 text:\nH₂/4 | |||
| bar:data41 from:1052 till:1753 color:limegreen | |||
| bar:data41 at:1753 text:\nH₂/3 | |||
| bar:data41 at:1315 text:H₂/4 mark:(line,white) | |||
| bar:data41 at:500 text:\nH₂/5 | |||
| bar:data02 from:2629 till:end color:skyblue | |||
| :<math>H = 7812.5 \mbox{ mm} \,</math> | |||
| bar:data02 at:13500 text:∞ | |||
| bar:data02 at:2604 text:\nH₃ − f₃ = 2604 mm | |||
| bar:data12 from:1315 till:end color:powderblue2 | |||
| bar:data12 at:13500 text:\n∞ | |||
| bar:data12 at:2629 text:H₃ = 2629 mm mark:(line,white) | |||
| bar:data12 at:1315 text:\nH₃/2 | |||
| bar:data22 from:876 till:2629 color:skyblue | |||
| bar:data22 at:2629 text:\nH₃ | |||
| bar:data22 at:1315 text:H₃/2 mark:(line,white) | |||
| bar:data22 at:876 text:\nH₃/3 | |||
| bar:data32 from:657 till:1315 color:skyblue | |||
| bar:data32 at:1315 text:\nH₃/2 | |||
| bar:data32 at:876 text:H₃/3 mark:(line,white) | |||
| bar:data32 at:0 text:\nH₃/4 | |||
| bar:data42 from:526 till:876 color:skyblue | |||
| bar:data42 at:876 text:\nH₃/3 | |||
| bar:data42 at:657 text:H₂/4 mark:(line,white) | |||
| bar:data42 at:0 text:\nH₃/5 | |||
| LineData = | |||
| at:2629 width:1 color:brightblue layer:back | |||
| TextData = | |||
| pos:(170,500) text:] | |||
| pos:(170,490) text:] | |||
| pos:(10,10) text:Distance of | |||
| pos:(10,0) text:object in mm | |||
| fontsize:L | |||
| pos:(475,0) text:→ ∞ | |||
| </timeline>|width=520|caption=] of 3 ideal ]es of ]s, {{math|''f''{{sub|1}}}}, {{math|''f''{{sub|2}}}} and {{math|''f''{{sub|3}}}}, and ]s {{math|''N''{{sub|1}}}}, {{math|''N''{{sub|2}}}}, and {{math|''N''{{sub|3}}}} when focused at objects at different distances. {{math|''H''{{sub|1}}}}, {{math|''H''{{sub|2}}}}, and {{math|''H''{{sub|#}}}} denote their respective hyperfocal distances (using ''Definition 1'' in that article) with a ] of {{val|0.03|u=mm}} diameter. The darker bars show how that, for fixed subject distance, the depth of field is increased by using a shorter focal length or smaller aperture. The second topmost bar of each set illustrates the configuration for a ] ] with the focus permanently set at the hyperfocal distance to maximise the depth of field. }} | |||
| As an example, for a {{val|50|u=mm}} lens at {{f/|8}} using a circle of confusion of {{val|0.03|u=mm}}, which is a value typically used in {{val|35|u=mm}} photography, the hyperfocal distance according to ''Definition 1'' is | |||
| The "optical" hyperfocal distance is about 7.8 m. To determine the "photographic" hyperfocal distance, we then compute D: | |||
| <math display="block">H = \frac{(50)^2}{(8)(0.03)} + (50) = 10467 \mbox{ mm}</math> | |||
| If the lens is focused at a distance of {{val|10.5|u=m}}, then everything from half that distance ({{val|5.2|u=m}}) to infinity will be acceptably sharp in our photograph. With the formula for the ''Definition 2'', the result is {{val|10417|u=mm}}, a difference of 0.5%. | |||
| :<math>D = 7862.5 \mbox{ mm} \,</math> | |||
| == Consecutive depths of field == | |||
| If we focus the lens at a distance of 7.9 m, then everything from half that distance (4 m) to infinity will be acceptably sharp in our photograph. | |||
| The hyperfocal distance has a curious property: while a lens focused at {{mvar|H}} will hold a depth of field from {{math|''H''/2}} to infinity, if the lens is focused to {{math|''H''/2}}, the depth of field will extend from {{math|''H''/3}} to {{mvar|H}}; if the lens is then focused to {{math|''H''/3}}, the depth of field will extend from {{math|''H''/4}} to {{math|''H''/2}}. This continues on through all successive neighboring terms in the ] ({{math|1/''x''}}) values of the hyperfocal distance. That is, focusing at {{math|''H''/''n''}} will cause the depth of field to extend from {{math|''H''/(''n'' + 1)}} to {{math|''H''/(''n'' − 1)}}. | |||
| C. Welborne Piper calls this phenomenon "consecutive depths of field" and shows how to test the idea easily. This is also among the earliest of publications to use the word ''hyperfocal''.<ref name="Piper1901" /> | |||
| ==Alternate usage== | |||
| ==History== | |||
| In informal usage, the focus point that allows a particular range of distances to be acceptably in focus at a particular aperture also is frequently called the hyperfocal distance. This is an extension of the concept of "photographic" hyperfocal distance to include depth of field ranges that do not extend to infinity. | |||
| ] | |||
| The concepts of the two definitions of hyperfocal distance have a long history, tied up with the terminology for depth of field, depth of focus, circle of confusion, etc. Here are some selected early quotations and interpretations on the topic. | |||
| ===Sutton and Dawson 1867=== | |||
| Thomas Sutton and George Dawson define ''focal range'' for what we now call ''hyperfocal distance'':<ref name=":0" /> | |||
| {{blockquote|Focal Range. In every lens there is, corresponding to a given apertal ratio (that is, the ratio of the diameter of the stop to the focal length), a certain distance of a near object from it, between which and infinity all objects are in equally good focus. For instance, in a single view lens of 6 inch focus, with a 1/4 in. stop (apertal ratio one-twenty-fourth), all objects situated at distances lying between 20 feet from the lens and an infinite distance from it (a fixed star, for instance) are in equally good focus. Twenty feet is therefore called the "focal range" of the lens when this stop is used. The focal range is consequently the distance of the nearest object, which will be in good focus when the ground glass is adjusted for an extremely distant object. In the same lens, the focal range will depend upon the size of the diaphragm used, while in different lenses having the same apertal ratio the focal ranges will be greater as the focal length of the lens is increased. | |||
| The terms 'apertal ratio' and 'focal range' have not come into general use, but it is very desirable that they should, in order to prevent ambiguity and circumlocution when treating of the properties of photographic lenses. 'Focal range' is a good term, because it expresses the range within which it is necessary to adjust the focus of the lens to objects at different distances from it – in other words, the range within which focusing becomes necessary.}} | |||
| Their focal range is about 1000 times their aperture diameter, so it makes sense as a hyperfocal distance with CoC value of {{f/|1000}}, or image format diagonal times 1/1000 assuming the lens is a "normal" lens. What is not clear, however, is whether the focal range they cite was computed, or empirical. | |||
| ===Abney 1881=== | |||
| Sir William de Wivelesley Abney says:<ref>{{cite book |first=W. de W. |last=Abney |title=A Treatise on Photography |edition=First |location=London |publisher=Longmans, Green, and Co. |year=1881 }}</ref> | |||
| {{blockquote|1=The annexed formula will approximately give the nearest point {{mvar|p}} which will appear in focus when the distance is accurately focussed, supposing the admissible disc of confusion to be {{val|0.025|u=cm}}: | |||
| <math display="block">p = 0.41 \cdot f^2 \cdot a</math> | |||
| when | |||
| * {{math|1=''f'' =}} the focal length of the lens in cm | |||
| * {{math|1=''a'' =}} the ratio of the aperture to the focal length}} | |||
| That is, {{mvar|a}} is the reciprocal of what we now call the f-number, and the answer is evidently in meters. His 0.41 should obviously be 0.40. Based on his formulae, and on the notion that the ''aperture ratio'' should be kept fixed in comparisons across formats, Abney says: | |||
| {{blockquote|It can be shown that an enlargement from a small negative is better than a picture of the same size taken direct as regards sharpness of detail. ... Care must be taken to distinguish between the advantages to be gained in enlargement by the use of a smaller lens, with the disadvantages that ensue from the deterioration in the relative values of light and shade.}} | |||
| ===Taylor 1892=== | |||
| John Traill Taylor recalls this word formula for a sort of hyperfocal distance:<ref>{{cite book |first=J. Traill |last=Taylor |url=https://archive.org/details/opticsofphotogra00taylrich |title=The Optics of Photography and Photographic Lenses |location=London |publisher=Whittaker & Co |year=1892 }}</ref> | |||
| {{blockquote|We have seen it laid down as an approximative rule by some writers on optics (Thomas Sutton, if we remember aright), that if the diameter of the stop be a fortieth part of the focus of the lens, the depth of focus will range between infinity and a distance equal to four times as many feet as there are inches in the focus of the lens.}} | |||
| This formula implies a stricter CoC criterion than we typically use today. | |||
| ===Hodges 1895=== | |||
| John Hodges discusses depth of field without formulas but with some of these relationships:<ref>{{cite book |first=John |last=Hodges |title=Photographic Lenses: How to Choose, and How to Use |location=Bradford |publisher=Percy Lund & Co |year=1895 }}</ref> | |||
| {{blockquote|There is a point, however, beyond which everything will be in pictorially good definition, but the longer the focus of the lens used, the further will the point beyond which everything is in sharp focus be removed from the camera. Mathematically speaking, the amount of depth possessed by a lens varies inversely as the square of its focus.}} | |||
| This "mathematically" observed relationship implies that he had a formula at hand, and a parameterization with the f-number or "intensity ratio" in it. To get an inverse-square relation to focal length, you have to assume that the CoC limit is fixed and the aperture diameter scales with the focal length, giving a constant f-number. | |||
| ===Piper 1901=== | |||
| C. Welborne Piper may be the first to have published a clear distinction between ''Depth of Field'' in the modern sense and ''Depth of Definition'' in the focal plane, and implies that ''Depth of Focus'' and ''Depth of Distance'' are sometimes used for the former (in modern usage, ''Depth of Focus'' is usually reserved for the latter).<ref name="Piper1901">{{cite book |first=C. Welborne |last=Piper |title=A First Book of the Lens: An Elementary Treatise on the Action and Use of the Photographic Lens |location=London |publisher=Hazell, Watson, and Viney |year=1901 }}</ref> He uses the term ''Depth Constant'' for {{mvar|H}}, and measures it from the front principal focus (i. e., he counts one focal length less than the distance from the lens to get the simpler formula), and even introduces the modern term: | |||
| {{blockquote|This is the maximum depth of field possible, and {{math|''H'' + ''f''}} may be styled the distance of maximum depth of field. If we measure this distance extra-focally it is equal to {{mvar|H}}, and is sometimes called the hyperfocal distance. The depth constant and the hyperfocal distance are quite distinct, though of the same value.}} | |||
| It is unclear what distinction he means. Adjacent to Table I in his appendix, he further notes: | |||
| {{blockquote|If we focus on infinity, the constant is the focal distance of the nearest object in focus. If we focus on an extra-focal distance equal to the constant, we obtain a maximum depth of field from approximately half the constant distance up to infinity. The constant is then the hyper-focal distance.}} | |||
| At this point we do not have evidence of the term ''hyperfocal'' before Piper, nor the hyphenated ''hyper-focal'' which he also used, but he obviously did not claim to coin this descriptor himself. | |||
| ===Derr 1906=== | |||
| Louis Derr may be the first to clearly specify the first definition,<ref>{{cite book |first=Louis |last=Derr |title=Photography for students of physics and chemistry |url=https://archive.org/details/cu31924031218674 |location=London |publisher=Macmillan |year=1906 }}</ref> which is considered to be the strictly correct one in modern times, and to derive the formula corresponding to it. Using {{mvar|p}} for hyperfocal distance, {{mvar|D}} for aperture diameter, {{mvar|d}} for the diameter that a circle of confusion shall not exceed, and {{mvar|f}} for focal length, he derives:<ref>{{Cite book |last=Derr |first=Louis |url=https://books.google.com/books?id=AN6d4zTjquwC&pg=PA78 |title=Photography for students of physics and chemistry |date=1906 |publisher=Macmillan Company; London, Macmillan & Company, Limited |language=en}}</ref> | |||
| <math display="block>p = \frac{(D + d) f}{d}\,.</math> | |||
| As the aperture diameter, {{mvar|D}} is the ratio of the focal length {{mvar|f}} to the numerical aperture {{mvar|N}} ({{math|1=''D'' = ''f''/''N''}}); and the diameter of the circle of confusion, {{math|1=''c'' = ''d''}}, this gives the equation for the first definition above. | |||
| <math display="block">p = \frac{\left(\tfrac{f}{N} + c\right) f}{c} = \frac{f^2}{N c} + f</math> | |||
| ===Johnson 1909=== | |||
| George Lindsay Johnson uses the term ''Depth of Field'' for what Abney called ''Depth of Focus,'' and ''Depth of Focus'' in the modern sense (possibly for the first time),<ref>{{cite book |first=George Lindsay |last=Johnson |title=Photographic Optics and Colour Photography |url=https://archive.org/details/photographicopt00johngoog |location=London |publisher=Ward & Co |year=1909 }}</ref> as the allowable distance error in the focal plane. His definitions include hyperfocal distance: | |||
| {{blockquote|1=Depth of Focus is a convenient, but not strictly accurate term, used to describe the amount of racking movement (forwards or backwards) which can be given to the screen without the image becoming sensibly blurred, i.e. without any blurring in the image exceeding 1/100 in., or in the case of negatives to be enlarged or scientific work, the 1/10 or 1/100 mm. Then the breadth of a point of light, which, of course, causes blurring on both sides, i.e. {{nowrap|1/50 in = 2{{mvar|e}}}} (or {{nowrap|1/100 in = {{mvar|e}}}}).}} | |||
| His drawing makes it clear that his {{mvar|e}} is the radius of the circle of confusion. He has clearly anticipated the need to tie it to format size or enlargement, but has not given a general scheme for choosing it. | |||
| {{blockquote|Depth of Field is precisely the same as depth of focus, only in the former case the depth is measured by the movement of the plate, the object being fixed, while in the latter case the depth is measured by the distance through which the object can be moved without the circle of confusion exceeding 2{{mvar|e}}. | |||
| Thus if a lens which is focused for infinity still gives a sharp image for an object at 6 yards, its depth of field is from infinity to 6 yards, every object beyond 6 yards being in focus. | |||
| This distance (6 yards) is termed the ''hyperfocal distance'' of the lens, and any allowable confusion disc depends on the focal length of the lens and on the stop used. | |||
| If the limit of confusion of half of the disc (i.e. {{mvar|e}}) be taken as 1/100 in., then the hyperfocal distance | |||
| <math display="block">H = \frac{F d}{e}\,,</math> | |||
| {{mvar|d}} being the diameter of the stop, ...}} | |||
| Johnson's use of ''former'' and ''latter'' seem to be swapped; perhaps ''former'' was here meant to refer to the immediately preceding section title ''Depth of Focus'', and ''latter'' to the current section title ''Depth of Field''. Except for an obvious factor-of-2 error in using the ratio of stop diameter to CoC radius, this definition is the same as Abney's hyperfocal distance. | |||
| ===Others, early twentieth century=== | |||
| The term ''hyperfocal distance'' also appears in Cassell's ''Cyclopaedia'' of 1911, ''The Sinclair Handbook of Photography'' of 1913, and Bayley's ''The Complete Photographer'' of 1914. | |||
| ===Kingslake 1951=== | |||
| ] is explicit about the two meanings:<ref name="Kingslake1951" /> | |||
| {{blockquote|if the camera is focused on a distance {{mvar|s}} equal to 1000 times the diameter of the lens aperture, then the far depth {{math|''D''{{sub|1}}}} becomes infinite. This critical object distance "{{mvar|h}}" is known as the ''Hyperfocal Distance''. For a camera focused on this distance, {{math|1=''D''{{sub|1}} = ∞}} and {{math|1=''D''{{sub|2}} = ''h''/2}}, and we see that the range of distances acceptably in focus will run from just half the hyperfocal distance to infinity. The hyperfocal distance is, therefore, the most desirable distance on which to pre-set the focus of a fixed-focus camera. It is worth noting, too, that if a camera is focused on {{math|1=''s'' = ∞}}, the closest acceptable object is at {{math|1=''L''{{sub|2}} = ''sh''/(''h'' + ''s'') = ''h''/(''h''/''s'' + 1) = ''h''}} (by equation 21). This is a second important meaning of the hyperfocal distance.}} | |||
| Kingslake uses the simplest formulae for DOF near and far distances, which has the effect of making the two different definitions of hyperfocal distance give identical values. | |||
| ==See also== | |||
| * ] | |||
| * ] | |||
| ==References== | |||
| {{reflist}} | |||
| ==External links== | ==External links== | ||
| *http://www.dofmaster.com/dofjs.html to calculate |
* http://www.dofmaster.com/dofjs.html to calculate hyperfocal distance and ] | ||
| *: real-world use for photographers, including its shortcomings and a hyperfocal chart calculator | |||
| {{Photography subject}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| <!-- Other languages --> | |||
| ] | |||
| ] | |||
Latest revision as of 12:40, 29 November 2024
Distance beyond which all objects can be brought into an acceptable focus


In optics and photography, hyperfocal distance is a distance from a lens beyond which all objects can be brought into an "acceptable" focus. As the hyperfocal distance is the focus distance giving the maximum depth of field, it is the most desirable distance to set the focus of a fixed-focus camera. The hyperfocal distance is entirely dependent upon what level of sharpness is considered to be acceptable.
The hyperfocal distance has a property called "consecutive depths of field", where a lens focused at an object whose distance from the lens is at the hyperfocal distance H will hold a depth of field from H/2 to infinity, if the lens is focused to H/2, the depth of field will be from H/3 to H; if the lens is then focused to H/3, the depth of field will be from H/4 to H/2, etc.
Thomas Sutton and George Dawson first wrote about hyperfocal distance (or "focal range") in 1867. Louis Derr in 1906 may have been the first to derive a formula for hyperfocal distance. Rudolf Kingslake wrote in 1951 about the two methods of measuring hyperfocal distance.
Some cameras have their hyperfocal distance marked on the focus dial. For example, on the Minox LX focusing dial there is a red dot between 2 m and infinity; when the lens is set at the red dot, that is, focused at the hyperfocal distance, the depth of field stretches from 2 m to infinity. Some lenses have markings indicating the hyperfocal range for specific f-stops, also called a depth-of-field scale.
Two methods
There are two common methods of defining and measuring hyperfocal distance, leading to values that differ only slightly. The distinction between the two meanings is rarely made, since they have almost identical values. The value computed according to the first definition exceeds that from the second by just one focal length.
- Definition 1
- The hyperfocal distance is the closest distance at which a lens can be focused while keeping objects at infinity acceptably sharp. When the lens is focused at this distance, all objects at distances from half of the hyperfocal distance out to infinity will be acceptably sharp.
- Definition 2
- The hyperfocal distance is the distance beyond which all objects are acceptably sharp, for a lens focused at infinity.
Acceptable sharpness
The hyperfocal distance is entirely dependent upon what level of sharpness is considered to be acceptable. The criterion for the desired acceptable sharpness is specified through the circle of confusion (CoC) diameter limit. This criterion is the largest acceptable spot size diameter that an infinitesimal point is allowed to spread out to on the imaging medium (film, digital sensor, etc.).
Formula
For the first definition,
where
- H is the hyperfocal distance;
- f is the focal length of the lens;
- N is f-number (f/D for aperture diameter D); and
- c is the circle of confusion limit.
For any practical f-number, the added focal length is insignificant in comparison with the first term, so that
This formula is exact for the second definition, if H is measured from a thin lens, or from the front principal plane of a complex lens; it is also exact for the first definition if H is measured from a point that is one focal length in front of the front principal plane. For practical purposes, there is little difference between the first and second definitions.
Derivation using geometric optics

The following derivations refer to the accompanying figures. For clarity, half the aperture and circle of confusion are indicated.
Definition 1
An object at distance H forms a sharp image at distance x (blue line). Here, objects at infinity have images with a circle of confusion indicated by the brown ellipse where the upper red ray through the focal point intersects the blue line.
First using similar triangles hatched in green,
Then using similar triangles dotted in purple,
as found above.
Definition 2
Objects at infinity form sharp images at the focal length f (blue line). Here, an object at H forms an image with a circle of confusion indicated by the brown ellipse where the lower red ray converging to its sharp image intersects the blue line.
Using similar triangles shaded in yellow,
Example
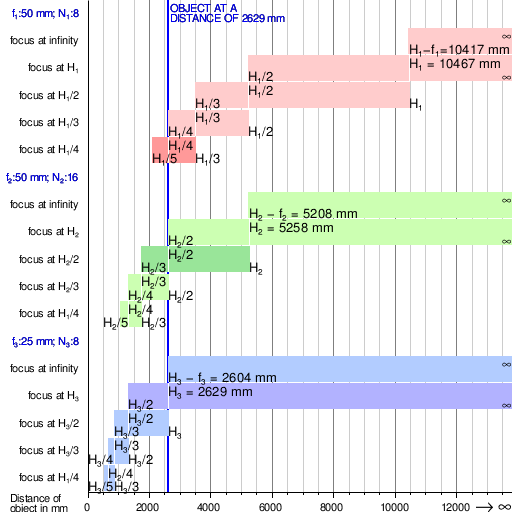 Depths of field of 3 ideal lenses of focal lengths, f1, f2 and f3, and f-numbers N1, N2, and N3 when focused at objects at different distances. H1, H2, and H# denote their respective hyperfocal distances (using Definition 1 in that article) with a circle of confusion of 0.03 mm diameter. The darker bars show how that, for fixed subject distance, the depth of field is increased by using a shorter focal length or smaller aperture. The second topmost bar of each set illustrates the configuration for a fixed focus camera with the focus permanently set at the hyperfocal distance to maximise the depth of field.
Depths of field of 3 ideal lenses of focal lengths, f1, f2 and f3, and f-numbers N1, N2, and N3 when focused at objects at different distances. H1, H2, and H# denote their respective hyperfocal distances (using Definition 1 in that article) with a circle of confusion of 0.03 mm diameter. The darker bars show how that, for fixed subject distance, the depth of field is increased by using a shorter focal length or smaller aperture. The second topmost bar of each set illustrates the configuration for a fixed focus camera with the focus permanently set at the hyperfocal distance to maximise the depth of field.
As an example, for a 50 mm lens at f/8 using a circle of confusion of 0.03 mm, which is a value typically used in 35 mm photography, the hyperfocal distance according to Definition 1 is
If the lens is focused at a distance of 10.5 m, then everything from half that distance (5.2 m) to infinity will be acceptably sharp in our photograph. With the formula for the Definition 2, the result is 10417 mm, a difference of 0.5%.
Consecutive depths of field
The hyperfocal distance has a curious property: while a lens focused at H will hold a depth of field from H/2 to infinity, if the lens is focused to H/2, the depth of field will extend from H/3 to H; if the lens is then focused to H/3, the depth of field will extend from H/4 to H/2. This continues on through all successive neighboring terms in the harmonic series (1/x) values of the hyperfocal distance. That is, focusing at H/n will cause the depth of field to extend from H/(n + 1) to H/(n − 1).
C. Welborne Piper calls this phenomenon "consecutive depths of field" and shows how to test the idea easily. This is also among the earliest of publications to use the word hyperfocal.
History

The concepts of the two definitions of hyperfocal distance have a long history, tied up with the terminology for depth of field, depth of focus, circle of confusion, etc. Here are some selected early quotations and interpretations on the topic.
Sutton and Dawson 1867
Thomas Sutton and George Dawson define focal range for what we now call hyperfocal distance:
Focal Range. In every lens there is, corresponding to a given apertal ratio (that is, the ratio of the diameter of the stop to the focal length), a certain distance of a near object from it, between which and infinity all objects are in equally good focus. For instance, in a single view lens of 6 inch focus, with a 1/4 in. stop (apertal ratio one-twenty-fourth), all objects situated at distances lying between 20 feet from the lens and an infinite distance from it (a fixed star, for instance) are in equally good focus. Twenty feet is therefore called the "focal range" of the lens when this stop is used. The focal range is consequently the distance of the nearest object, which will be in good focus when the ground glass is adjusted for an extremely distant object. In the same lens, the focal range will depend upon the size of the diaphragm used, while in different lenses having the same apertal ratio the focal ranges will be greater as the focal length of the lens is increased. The terms 'apertal ratio' and 'focal range' have not come into general use, but it is very desirable that they should, in order to prevent ambiguity and circumlocution when treating of the properties of photographic lenses. 'Focal range' is a good term, because it expresses the range within which it is necessary to adjust the focus of the lens to objects at different distances from it – in other words, the range within which focusing becomes necessary.
Their focal range is about 1000 times their aperture diameter, so it makes sense as a hyperfocal distance with CoC value of f/1000, or image format diagonal times 1/1000 assuming the lens is a "normal" lens. What is not clear, however, is whether the focal range they cite was computed, or empirical.
Abney 1881
Sir William de Wivelesley Abney says:
The annexed formula will approximately give the nearest point p which will appear in focus when the distance is accurately focussed, supposing the admissible disc of confusion to be 0.025 cm:
when
- f = the focal length of the lens in cm
- a = the ratio of the aperture to the focal length
That is, a is the reciprocal of what we now call the f-number, and the answer is evidently in meters. His 0.41 should obviously be 0.40. Based on his formulae, and on the notion that the aperture ratio should be kept fixed in comparisons across formats, Abney says:
It can be shown that an enlargement from a small negative is better than a picture of the same size taken direct as regards sharpness of detail. ... Care must be taken to distinguish between the advantages to be gained in enlargement by the use of a smaller lens, with the disadvantages that ensue from the deterioration in the relative values of light and shade.
Taylor 1892
John Traill Taylor recalls this word formula for a sort of hyperfocal distance:
We have seen it laid down as an approximative rule by some writers on optics (Thomas Sutton, if we remember aright), that if the diameter of the stop be a fortieth part of the focus of the lens, the depth of focus will range between infinity and a distance equal to four times as many feet as there are inches in the focus of the lens.
This formula implies a stricter CoC criterion than we typically use today.
Hodges 1895
John Hodges discusses depth of field without formulas but with some of these relationships:
There is a point, however, beyond which everything will be in pictorially good definition, but the longer the focus of the lens used, the further will the point beyond which everything is in sharp focus be removed from the camera. Mathematically speaking, the amount of depth possessed by a lens varies inversely as the square of its focus.
This "mathematically" observed relationship implies that he had a formula at hand, and a parameterization with the f-number or "intensity ratio" in it. To get an inverse-square relation to focal length, you have to assume that the CoC limit is fixed and the aperture diameter scales with the focal length, giving a constant f-number.
Piper 1901
C. Welborne Piper may be the first to have published a clear distinction between Depth of Field in the modern sense and Depth of Definition in the focal plane, and implies that Depth of Focus and Depth of Distance are sometimes used for the former (in modern usage, Depth of Focus is usually reserved for the latter). He uses the term Depth Constant for H, and measures it from the front principal focus (i. e., he counts one focal length less than the distance from the lens to get the simpler formula), and even introduces the modern term:
This is the maximum depth of field possible, and H + f may be styled the distance of maximum depth of field. If we measure this distance extra-focally it is equal to H, and is sometimes called the hyperfocal distance. The depth constant and the hyperfocal distance are quite distinct, though of the same value.
It is unclear what distinction he means. Adjacent to Table I in his appendix, he further notes:
If we focus on infinity, the constant is the focal distance of the nearest object in focus. If we focus on an extra-focal distance equal to the constant, we obtain a maximum depth of field from approximately half the constant distance up to infinity. The constant is then the hyper-focal distance.
At this point we do not have evidence of the term hyperfocal before Piper, nor the hyphenated hyper-focal which he also used, but he obviously did not claim to coin this descriptor himself.
Derr 1906
Louis Derr may be the first to clearly specify the first definition, which is considered to be the strictly correct one in modern times, and to derive the formula corresponding to it. Using p for hyperfocal distance, D for aperture diameter, d for the diameter that a circle of confusion shall not exceed, and f for focal length, he derives:
As the aperture diameter, D is the ratio of the focal length f to the numerical aperture N (D = f/N); and the diameter of the circle of confusion, c = d, this gives the equation for the first definition above.
Johnson 1909
George Lindsay Johnson uses the term Depth of Field for what Abney called Depth of Focus, and Depth of Focus in the modern sense (possibly for the first time), as the allowable distance error in the focal plane. His definitions include hyperfocal distance:
Depth of Focus is a convenient, but not strictly accurate term, used to describe the amount of racking movement (forwards or backwards) which can be given to the screen without the image becoming sensibly blurred, i.e. without any blurring in the image exceeding 1/100 in., or in the case of negatives to be enlarged or scientific work, the 1/10 or 1/100 mm. Then the breadth of a point of light, which, of course, causes blurring on both sides, i.e. {{{1}}} (or {{{1}}}).
His drawing makes it clear that his e is the radius of the circle of confusion. He has clearly anticipated the need to tie it to format size or enlargement, but has not given a general scheme for choosing it.
Depth of Field is precisely the same as depth of focus, only in the former case the depth is measured by the movement of the plate, the object being fixed, while in the latter case the depth is measured by the distance through which the object can be moved without the circle of confusion exceeding 2e.
Thus if a lens which is focused for infinity still gives a sharp image for an object at 6 yards, its depth of field is from infinity to 6 yards, every object beyond 6 yards being in focus.
This distance (6 yards) is termed the hyperfocal distance of the lens, and any allowable confusion disc depends on the focal length of the lens and on the stop used.
If the limit of confusion of half of the disc (i.e. e) be taken as 1/100 in., then the hyperfocal distance
d being the diameter of the stop, ...
Johnson's use of former and latter seem to be swapped; perhaps former was here meant to refer to the immediately preceding section title Depth of Focus, and latter to the current section title Depth of Field. Except for an obvious factor-of-2 error in using the ratio of stop diameter to CoC radius, this definition is the same as Abney's hyperfocal distance.
Others, early twentieth century
The term hyperfocal distance also appears in Cassell's Cyclopaedia of 1911, The Sinclair Handbook of Photography of 1913, and Bayley's The Complete Photographer of 1914.
Kingslake 1951
Rudolf Kingslake is explicit about the two meanings:
if the camera is focused on a distance s equal to 1000 times the diameter of the lens aperture, then the far depth D1 becomes infinite. This critical object distance "h" is known as the Hyperfocal Distance. For a camera focused on this distance, D1 = ∞ and D2 = h/2, and we see that the range of distances acceptably in focus will run from just half the hyperfocal distance to infinity. The hyperfocal distance is, therefore, the most desirable distance on which to pre-set the focus of a fixed-focus camera. It is worth noting, too, that if a camera is focused on s = ∞, the closest acceptable object is at L2 = sh/(h + s) = h/(h/s + 1) = h (by equation 21). This is a second important meaning of the hyperfocal distance.
Kingslake uses the simplest formulae for DOF near and far distances, which has the effect of making the two different definitions of hyperfocal distance give identical values.
See also
References
- ^ Kingslake, Rudolf (1951). Lenses in Photography: The Practical Guide to Optics for Photographers. Garden City, NY: Garden City Press.
- ^ Sutton, Thomas; Dawson, George (1867). A Dictionary of Photography. London: Sampson Low, Son & Marston.
- Minolta (1985). Minolta MD Zoom Lenses owner's manual. p. 9.
- Kingslake, Rudolf (1992). Optics in Photography - Google Books. SPIE Press. ISBN 9780819407634. Retrieved 24 September 2014.
- ^ Piper, C. Welborne (1901). A First Book of the Lens: An Elementary Treatise on the Action and Use of the Photographic Lens. London: Hazell, Watson, and Viney.
- Abney, W. de W. (1881). A Treatise on Photography (First ed.). London: Longmans, Green, and Co.
- Taylor, J. Traill (1892). The Optics of Photography and Photographic Lenses. London: Whittaker & Co.
- Hodges, John (1895). Photographic Lenses: How to Choose, and How to Use. Bradford: Percy Lund & Co.
- Derr, Louis (1906). Photography for students of physics and chemistry. London: Macmillan.
- Derr, Louis (1906). Photography for students of physics and chemistry. Macmillan Company; London, Macmillan & Company, Limited.
- Johnson, George Lindsay (1909). Photographic Optics and Colour Photography. London: Ward & Co.
External links
- http://www.dofmaster.com/dofjs.html to calculate hyperfocal distance and depth of field






 when
when


