| Revision as of 09:45, 8 March 2006 view sourceTawkerbot2 (talk | contribs)131,306 editsm vandalism from User talk:83.104.72.246 (42786879) - reverted to User talk:Dogears (42212581)← Previous edit | Latest revision as of 15:07, 15 November 2024 view source Constant314 (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers13,419 edits Reverted good faith edits by Goodphy (talk): Already in the articleTags: Twinkle Undo | ||
| Line 1: | Line 1: | ||
| {{short description|Flow of electric charge}} | |||
| {{backlink|Electricity}} | |||
| {{pp-vandalism|small=yes}} | |||
| {{TOCright}} | |||
| {{Infobox physical quantity | |||
| '''Electric current''' is the flow of ]. Natural examples include ] and the ], the source of the ]. The most familiar artificial form of electric current is the flow of ] ]s in metal ]s, such as the overhead power lines that deliver ] across long distances and the smaller wires within electrical and electronic equipment. In ], other forms of electric current include the flow of electrons through ]s or through the vacuum in a ], the flow of ]s inside a ], and the flow of ] within a ]. | |||
| | name = Electric current | |||
| | image = Ohm's Law with Voltage source TeX.svg | |||
| | caption = A simple electric circuit, where current is represented by the letter ''i''. The relationship between the voltage (''V''), resistance (''R''), and current (''i'' or ''I'') is ''V=IR''; this is known as ]. | |||
| | unit = ] | |||
| | otherunits = | |||
| | symbols = ''I'' | |||
| | baseunits = | |||
| | dimension = <math>\mathsf I</math> | |||
| | extensive = | |||
| | intensive = | |||
| | conserved = | |||
| | transformsas = | |||
| | derivations = <math>I = {V \over R} , I = {Q \over t} </math> | |||
| }}{{Electromagnetism|Network}} | |||
| An '''electric current''' is a flow of ]s, such as ]s or ]s, moving through an ] or space. It is defined as the net rate of flow of ] through a surface.<ref name="horowitz">{{cite book|last1=Horowitz|first1=Paul|title=The art of electronics|last2=Hill|first2=Winfield|date=2015|publisher=]|isbn=978-0-521-80926-9|edition=3rd|author-link1=Paul Horowitz (scientist)|author-link2=Winfield Hill}}</ref>{{rp|2}}<ref name="Walker">{{Cite book|last1=Walker|first1=Jearl|title=Fundamentals of physics|last2=Halliday|first2=David|last3=Resnick|first3=Robert|date=2014|publisher=Wiley|isbn=978-1118230732|edition=10th|location=Hoboken, NJ|oclc=950235056}}</ref>{{rp|622}} The moving particles are called ]s, which may be one of several types of particles, depending on the ]. In ]s the charge carriers are often ]s moving through a ]. In ]s they can be electrons or ]. In an ] the charge carriers are ]s, while in ], an ] gas, they are ions and electrons.<ref>{{cite book | |||
| == Relation between current and charge == | |||
| | title = The electronics companion | |||
| | author = Anthony C. Fischer-Cripps | |||
| | publisher = CRC Press | |||
| | year = 2004 | |||
| | isbn = 978-0-7503-1012-3 | |||
| | page = 13 | |||
| | url = https://books.google.com/books?id=3SsYctmvZkoC&pg=PA13 | |||
| }}</ref> | |||
| In the ] (SI), electric current is expressed in ] of ] (sometimes called an "amp", symbol A), which is equivalent to one ] per second. The ampere is an ] and electric current is a ] in the ] (ISQ).<ref name="SI">{{SIbrochure9th}}</ref>{{rp|15}} Electric current is also known as '''amperage''' and is measured using a device called an '']''.<ref name=Walker/>{{rp|788}} | |||
| The symbol typically used for the amount of current (the amount of charge ''Q'' flowing per unit of time ''t'') is '''''I''''', from the German word ''Intensität'', which means 'intensity'. | |||
| Electric currents create ], which are used in motors, generators, ]s, and ]s. In ordinary conductors, they cause ], which creates ] in ]. Time-varying currents emit ], which are used in ] to broadcast information. | |||
| :<math>I = {dQ \over dt}</math> | |||
| ==Symbol== | |||
| Formally this is written as | |||
| The conventional symbol for current is {{math|''I''}}, which originates from the French phrase {{lang|fr|intensité du courant}}, (current intensity).<ref>{{cite book|first1=T. L.|last1=Lowe|first2=John|last2=Rounce|title=Calculations for A-level Physics|page=2|publisher=Nelson Thornes|year=2002|isbn=0748767487}}</ref><ref>{{cite book|first1=Howard M.|last1=Berlin|first2=Frank C.|last2=Getz|title=Principles of Electronic Instrumentation and Measurement|page=37|publisher=Merrill Pub. Co.|year=1988|isbn=0675204496}}</ref> Current intensity is often referred to simply as ''current''.<ref>{{cite book|first1=K. S. Suresh|last1=Kumar|title=Electric Circuit Analysis|publisher=Pearson Education India|year=2013|isbn=978-9332514102|chapter=Section 1.2.3|quote='Current intensity' is usually referred to as 'current' itself.}}</ref> The {{math|''I''}} symbol was used by ], after whom the unit of electric current is named, in formulating ] (1820).<ref>{{cite web|first=A-M|last=Ampère|url=http://www.ampere.cnrs.fr/textes/recueil/pdf/recueilobservationsd.pdf |archive-url=https://web.archive.org/web/20110724083412/http://www.ampere.cnrs.fr/textes/recueil/pdf/recueilobservationsd.pdf |archive-date=2011-07-24 |url-status=live|title=Recueil d'Observations Électro-dynamiques|page=56|location=Paris: Chez Crochard Libraire|year=1822|language=French}}</ref> The notation travelled from France to Great Britain, where it became standard, although at least one journal did not change from using {{math|''C''}} to {{math|''I''}} until 1896.<ref>{{cite book|url=https://books.google.com/books?id=BCZLAAAAYAAJ|title=Electric Power|year=1894 |volume=6|pages=411, 1894}}</ref> | |||
| =={{anchor|Current}}Conventions==<!-- This section is linked from ] and ] --> | |||
| :<math>i(t) = {dq(t) \over dt}</math> or inversely as <math>q(t_0) = \int_{-\infty}^{t_0} i(t)\, dt</math> | |||
| ]s, the ]s in an electrical circuit, flow in the opposite direction of the conventional electric current.]] | |||
| ] for a battery in a ].]] | |||
| The conventional direction of current, also known as ''conventional current'',<ref name="Avison">{{cite book | |||
| == Conventional current == | |||
| | last1 = Avison | |||
| | first1 = John | |||
| | title = The World of Physics | |||
| | publisher = Thomas Nelson and Sons | |||
| | date = 2014 | |||
| | pages = 221 | |||
| | url = https://books.google.com/books?id=DojwZzKAvN8C&dq=%22conventional+current%22+positive+charge&pg=PA221 | |||
| | doi = | |||
| | id = | |||
| | isbn = 9780174387336 | |||
| }}</ref><ref name="McComb">{{cite book | |||
| | last1 = McComb | |||
| | first1 = Gordon | |||
| | last2 = Boysen | |||
| | first2 = Earl | |||
| | title = Electronics For Dummies | |||
| | publisher = Wiley | |||
| | date = 2005 | |||
| | pages = 12 | |||
| | url = https://books.google.com/books?id=CvLkgK8PBJkC&dq=%22conventional+current%22&pg=PA12 | |||
| | doi = | |||
| | id = | |||
| | isbn = 9780764597190 | |||
| }}</ref> is arbitrarily defined as the direction in which {{em|positive}} charges flow. In a ], the moving charged particles that constitute the electric current are called ]s. In metals, which make up the wires and other conductors in most ]s, the positively charged ] of the atoms are held in a fixed position, and the negatively charged ]s are the charge carriers, free to move about in the metal. In other materials, notably the ]s, the charge carriers can be positive ''or'' negative, depending on the ] used. Positive and negative charge carriers may even be present at the same time, as happens in an ] in an ]. | |||
| A flow of positive charges gives the same electric current, and has the same effect in a circuit, as an equal flow of negative charges in the opposite direction. Since current can be the flow of either positive or negative charges, or both, a convention is needed for the direction of current that is independent of the type of ]s. Negatively charged carriers, such as the electrons (the charge carriers in metal wires and many other electronic circuit components), therefore flow in the opposite direction of conventional current flow in an electrical circuit.<ref name="Avison" /><ref name="McComb" /> | |||
| '''Conventional current''' was defined early in the history of electrical science as a flow of positive charge. In solid metals, like wires, the positive charges are immobile, and only the negatively charged ]s flow in the direction opposite conventional current, but this is not the case in most non-metallic conductors. In other materials, charged particles flow in both directions at the same time. Electric currents in ] are flows of electrically charged atoms (]s), which exist in both positive and negative varieties. For example, an ] cell may be constructed with salt water (a solution of ]) on one side of a membrane and pure water on the other. The membrane lets the positive sodium ions pass, but not the negative chlorine ions, so a net current results. Electric currents in ] are flows of electrons as well as positive and negative ions. In ice and in certain solid electrolytes, flowing ]s constitute the electric current. To simplify this situation, the original definition of conventional current still stands. | |||
| ===Reference direction=== | |||
| There are also instances where the electrons are the charge that is physically moving, but where it makes more sense to think of the current as the movement of positive "]" (the spots that should have an electron to make the conductor neutral). This is the case in a p-type ]. | |||
| A current in a wire or ] can flow in either of two directions. When defining a ] <math>I</math> to represent the current, the direction representing positive current must be specified, usually by an arrow on the ] ].<ref name="Kumar">{{cite book | |||
| | last = Kumar | |||
| | first = K. S. Suresh | |||
| | title = Electric Circuits & Networks | |||
| | publisher = Pearson Education India | |||
| | year = 2008 | |||
| | location = | |||
| | pages = 26–28 | |||
| | url = https://books.google.com/books?id=ZzeXM-IQnIUC&pg=PA278 | |||
| | doi = | |||
| | id = | |||
| | isbn = 978-8131713907}}</ref><ref name="Hayt5">{{Cite book |last=Hayt |first= William |year= 1989 |title= Engineering Electromagnetics |edition= 5th |publisher= McGraw-Hill |isbn= 0070274061}}</ref>{{rp|13}} This is called the ''reference direction'' of the current <math>I</math>. When ], the actual direction of current through a specific circuit element is usually unknown until the analysis is completed. Consequently, the reference directions of currents are often assigned arbitrarily. When the circuit is solved, a negative value for the current implies the actual direction of current through that circuit element is opposite that of the chosen reference direction.{{efn| Our first step in the analysis is the assumption of reference directions for the unknown currents.<ref name="Hayt5"></ref>}}{{rp|29}} | |||
| ==Ohm's law== | |||
| The ] unit of electrical current is the ]. Electric current is therefore sometimes informally referred to as '''''amperage''''' or '''''ampage''''', by analogy with the term '']''. Though this is a valid term, some engineers frown on it. | |||
| {{Main|Ohm's law}} | |||
| Ohm's law states that the current through a conductor between two points is directly ] to the ] across the two points. Introducing the constant of proportionality, the ],<ref>{{cite book | |||
| == The drift speed of an electric current == | |||
| | title = Automotive ignition systems | |||
| The mobile charged particles within a conductor move constantly in random directions. In order for a net flow of charge to exist, the particles must also move together with an average drift rate. For example, during currents in ]s the particles follow an erratic path, bouncing from atom to atom, but generally drifting in the direction of the ]. The speed at which they drift can be calculated from the equation: | |||
| |author1=Consoliver, Earl L. |author2=Mitchell, Grover I. | |||
| :<math>I=nAvQ \!\ </math> | |||
| | publisher = McGraw-Hill | |||
| where | |||
| | year = 1920 | |||
| :''I'' is the current | |||
| | page = | |||
| :''n'' is number of charged particles '''per unit volume''' | |||
| | url = https://archive.org/details/automotiveignit03divigoog | |||
| :''A'' is the cross-sectional area of the conductor | |||
| | quote = ohm's law current proportional voltage resistance. | |||
| :''v'' is the drift velocity, and | |||
| }}</ref> one arrives at the usual mathematical equation that describes this relationship:<ref name=Millikan>{{cite book | |||
| :''Q'' is the charge on each particle. | |||
| | title = Elements of Electricity | |||
| Electric currents in solid matter are typically very slow flows. For example, in a ] ] of cross-section 0.5 mm², carrying a current of 5 A, the '']'' of the electrons is of the order of a millimetre per second. To take a different example, in the near-vacuum inside a ], the electrons travel in near-straight lines ("ballistically") at about a tenth of the ]. | |||
| | author = ] and E. S. Bishop | |||
| | publisher = American Technical Society | |||
| | year = 1917 | |||
| | page = | |||
| | url = https://archive.org/details/elementselectri00bishgoog | |||
| | quote = Ohm's law current directly proportional. | |||
| }}</ref> | |||
| <math display=block>I = \frac{V}{R},</math> | |||
| where ''I'' is the current through the conductor in units of ]s, ''V'' is the potential difference measured ''across'' the conductor in units of ]s, and ''R'' is the ] of the conductor in units of ]s. More specifically, Ohm's law states that the ''R'' in this relation is constant, independent of the current.<ref>{{cite book | |||
| However, we know that electric current ] are waves which propagate at very high speed. As with any wave, the speed of the waves in a medium have little relation to the speed of that medium as it moves. For example, in ], the waves of current propagate rapidly from a source to a distant ], while the charges themselves only move back and forth over a tiny distance. The velocity of flowing charges can be quite low. Yet, any changes in electric current can travel at the speed of light, though it might be slower in certain media. The percentage of speed in a medium compared to the speed of light in vacuum is called ], and is proportional to ]. | |||
| | title = Electrical papers | |||
| | volume = 1 | |||
| | author = Oliver Heaviside | |||
| | publisher = Macmillan and Co | |||
| | year = 1894 | |||
| | page = 283 | |||
| | url = https://books.google.com/books?id=lKV-AAAAMAAJ&q=ohm's%20law%20constant%20ratio&pg=PA284 | |||
| | isbn = 978-0-8218-2840-3 | |||
| }}</ref> | |||
| ==Alternating and direct current== | |||
| == Current density == | |||
| {{Anchor|AC and DC}} | |||
| {{See also|War of the currents}} | |||
| In ] (AC) systems, the movement of ] periodically reverses direction. AC is the form of ] most commonly delivered to businesses and residences. The usual ] of an ] circuit is a ], though certain applications use alternative waveforms, such as ] or ]s. ] and ] signals carried on electrical wires are also examples of alternating current. An important goal in these applications is recovery of information encoded (or '']'') onto the AC signal. | |||
| In contrast, ] (DC) refers to a system in which the movement of electric charge in only one direction (sometimes called unidirectional flow). Direct current is produced by sources such as ], ]s, ]s, and ]-type electric machines of the ] type. Alternating current can also be converted to direct current through use of a ]. Direct current may flow in a ] such as a wire, but can also flow through ]s, ], or even through a ] as in ]. An ] for direct current was ''galvanic current''.<ref>{{cite book |title=Clinical Electrophysiology: Electrotherapy and Electrophysiologic Testing |author1=Andrew J. Robinson |author2=Lynn Snyder-Mackler |edition=3rd|year=2007 |publisher= Lippincott Williams & Wilkins|isbn= 978-0-7817-4484-3|page=10|url=https://books.google.com/books?id=C2-9bcIjPBsC&q=%22galvanic+current%22+%22direct+current%22&pg=PA10}}</ref> | |||
| '''Current density''' is the current per unit (cross-sectional) area. | |||
| ==Occurrences== | |||
| Mathematically, current is defined as the net flux through an area. Thus: | |||
| Natural observable examples of electric current include ], ], and the ], the source of the ]s. | |||
| Man-made occurrences of electric current include the flow of conduction electrons in metal wires such as the overhead power lines that deliver ] across long distances and the smaller wires within electrical and electronic equipment. ]s are electric currents that occur in conductors exposed to changing magnetic fields. Similarly, electric currents occur, particularly in the surface, of conductors exposed to ]s. When oscillating electric currents flow at the correct voltages within ]s, ]s are generated. | |||
| :<math> | |||
| I = j \cdot A | |||
| </math> | |||
| In ], other forms of electric current include the flow of electrons through ]s or through the vacuum in a ], the flow of ions inside a ], and the flow of ] within metals and ]s. | |||
| where, in the MKS or ] system of measurement, | |||
| A biological example of current is the flow of ions in ] and nerves, responsible for both thought and sensory perception. | |||
| :''I'' is the current, measured in ]s | |||
| :''j'' is the "current density" measured in amperes per ] | |||
| :''A'' is the area through which the current is flowing, measured in ]s | |||
| ==Measurement== | |||
| The current density is defined as: | |||
| Current can be measured using an ]. | |||
| Electric current can be directly measured with a ], but this method involves breaking the ], which is sometimes inconvenient. | |||
| :<math> | |||
| j=\int_i n_i \cdot x_i \cdot \mathbf{u_i} | |||
| </math> | |||
| Current can also be measured without breaking the circuit by detecting the magnetic field associated with the current. | |||
| where | |||
| Devices, at the circuit level, use various ] to measure current: | |||
| * ]s<ref>{{cite web|url=http://www.ti.com/analog/docs/microsite.tsp?sectionId=560&tabId=2180µsiteId=7|title=What is a Current Sensor and How is it Used?|access-date=2011-12-22}}</ref> | |||
| * ] current sensor transducers | |||
| * ] (however DC cannot be measured) | |||
| * ] field sensors<ref>{{cite news|first1=Andreas P.|last1=Friedrich|first2=Helmuth|last2=Lemme|url=http://www.sensorsmag.com/sensors/electric-magnetic/the-universal-current-sensor-1029|title=The Universal Current Sensor|archive-url=https://web.archive.org/web/20160304051430/http://www.sensorsmag.com/sensors/electric-magnetic/the-universal-current-sensor-1029 |archive-date=2016-03-04|newspaper=Fierce Electronics|date=2000-05-01|access-date=2011-12-22}}</ref> | |||
| * ]s | |||
| * ]s | |||
| ==Resistive heating== | |||
| :''n'' is the particle density (number of particles per unit volume) | |||
| {{Main|Joule heating}} | |||
| :''x'' is the mass, charge, or any other characteristic whose flow one would like to measure. | |||
| Joule heating, also known as ''ohmic heating'' and ''resistive heating'', is the process of ]<ref name="JaffeTaylor">{{cite book |last1=Jaffe |first1=Robert L. |last2=Taylor |first2=Washington |title=The physics of energy |date=2018 |publisher=Cambridge University Press }}</ref>{{rp|36}} by which the passage of an electric current through a ] increases the ] of the conductor,<ref name="SerwayJewett2004">{{cite book|last=Serway|first=Raymond A.|url=https://archive.org/details/physicssciengv2p00serw|title=Physics for Scientists and Engineers|author2=Jewett, John W.|publisher=Thomson Brooks/Cole|year=2004|isbn=0-534-40842-7|edition=6th|url-access=registration}}</ref>{{rp|846}} converting ] into ].<ref name="SerwayJewett2004"/>{{rp|846, fn. 5}} The phenomenon was first studied by ] in 1841. Joule immersed a length of wire in a fixed ] of ] and measured the ] rise due to a known current through the wire for a 30 ] period. By varying the current and the length of the wire he deduced that the heat produced was ] to the ] of the current multiplied by the ] of the wire. | |||
| :''u'' is the average velocity of the particles in each volume | |||
| <math display=block>P \propto I^2 R. </math> | |||
| Current density is an important consideration in the design of electrical and electronic systems. Most electrical conductors have a finite, positive resistance, making them dissipate power in the form of heat. The current density must be kept sufficiently low to prevent the conductor from melting or burning up, or the insulating material failing. In ], excessive current density may generate a strong enough magnetic field to cause spontaneous loss of the superconductive property. | |||
| This relationship is known as ].<ref name="JaffeTaylor"/>{{rp|36}} The ] of ] was subsequently named the ] and given the symbol ''J''.<ref name="SI"/>{{rp|20}} The commonly known SI unit of power, the ] (symbol: W), is equivalent to one joule per second.<ref name="SI"/>{{rp|20}} | |||
| == Electromagnetism == | |||
| ==Electromagnetism== | |||
| Every electric current produces a ]. The magnetic field can be visualized as a pattern of circular field lines surrounding the wire. | |||
| {{Main|Electromagnetism}} | |||
| ===Electromagnet=== | |||
| {{Main|Electromagnet}} | |||
| ].]] | |||
| In an electromagnet a coil of wires behaves like a ] when an electric current flows through it. When the current is switched off, the coil loses its magnetism immediately. | |||
| Electric current produces a ]. The magnetic field can be visualized as a pattern of circular field lines surrounding the wire that persists as long as there is current. | |||
| ===Electromagnetic induction=== | |||
| Electric current can be directly measured with a ], but this method involves breaking the circuit, which is sometimes inconvenient. Current can also be measured without breaking the circuit by detecting the ] it creates. Devices used for this include ] ]s, ]s and ]s. | |||
| {{Main|Electromagnetic induction}} | |||
| ].]] | |||
| Magnetic fields can also be used to make electric currents. When a changing magnetic field is applied to a conductor, an ] (EMF) is induced,<ref name="SerwayJewett2004" />{{rp|1004}} which starts an electric current, when there is a suitable path. | |||
| == |
===Radio waves=== | ||
| {{Main|Radio waves}} | |||
| {{Further|Radio-frequency current}} | |||
| When an electric current flows in a ] at ], ] can be generated. These travel at the ] and can cause electric currents in distant conductors. | |||
| {{clear}} | |||
| ] predicts the current in an (ideal) ] (or other ]) to be the quotient of applied ] over ]: | |||
| ==Conduction mechanisms in various media== | |||
| :<math> | |||
| {{Main|Electrical conductivity|Charge transport mechanisms}} | |||
| I = \frac{V}{R} | |||
| In metallic solids, electric charge flows by means of ]s, from lower to higher ]. In other media, any stream of charged objects (ions, for example) may constitute an electric current. To provide a definition of current independent of the type of charge carriers, ''conventional current'' is defined as moving in the same direction as the positive charge flow. So, in metals where the charge carriers (electrons) are negative, conventional current is in the opposite direction to the overall electron movement. In conductors where the charge carriers are positive, conventional current is in the same direction as the charge carriers. | |||
| </math> | |||
| In a ], a beam of ions or electrons may be formed. In other conductive materials, the electric current is due to the flow of both positively and negatively charged particles at the same time. In still others, the current is entirely due to ]. For example, the electric currents in ]s are flows of positively and negatively charged ions. In a common lead-acid ] cell, electric currents are composed of positive ] ions flowing in one direction, and negative sulfate ions flowing in the other. Electric currents in ] or ] are flows of electrons as well as positive and negative ions. In ice and in certain solid electrolytes, the electric current is entirely composed of flowing ions. | |||
| where | |||
| === Metals === | |||
| :''I'' is the current, measured in ]s | |||
| :''V'' is the ] measured in ]s | |||
| :''R'' is the ] measured in ]s | |||
| In a ], some of the outer electrons in each atom are not bound to the individual molecules as they are in ]s, or in full bands as they are in insulating materials, but are free to move within the ]. These ]s can serve as ]s, carrying a current. Metals are particularly conductive because there are many of these free electrons. With no external ] applied, these electrons move about randomly due to ] but, on average, there is zero net current within the metal. At room temperature, the average speed of these random motions is 10<sup>6</sup> metres per second.<ref>{{cite web|url=http://library.thinkquest.org/C0111709/English/DC-Circuts/mechanism.html|title=The Mechanism Of Conduction In Metals|archive-url=https://web.archive.org/web/20121025004809/http://library.thinkquest.org/C0111709/English/DC-Circuts/mechanism.html|archive-date=2012-10-25|website=Think Quest}}</ref> Given a surface through which a metal wire passes, electrons move in both directions across the surface at an equal rate. As ] wrote in his ] book, '']'' (1947), "The metallic substances differ from all other materials by the fact that the outer shells of their atoms are bound rather loosely, and often let one of their electrons go free. Thus the interior of a metal is filled up with a large number of unattached electrons that travel aimlessly around like a crowd of displaced persons. When a metal wire is subjected to electric force applied on its opposite ends, these free electrons rush in the direction of the force, thus forming what we call an electric current." | |||
| == Electrical safety == | |||
| When a metal wire is connected across the two terminals of a ] ] such as a ], the source places an electric field across the conductor. The moment contact is made, the free electrons of the conductor are forced to drift toward the ] terminal under the influence of this field. The free electrons are therefore the ] in a typical solid conductor. | |||
| The most obvious hazard is electric shock, where a current through part of the body can cause effects from a slight tingle to cardiac arrest or severe burns. It is the current that passes that determines the effect, and this depends on the nature of the contact, the condition of the body part, the current path through the body and the voltage of the source. The effect also varies considerably from individual to individual. (For approximate figures see '''Shock Effects''' under ].) Because of this and because in practical situations the current that may pass cannot be predicted any supply of over 24 volts should be considered a possible source of dangerous electric shock. In particular note that 110 volts can certainly be lethal. | |||
| For a steady flow of charge through a surface, the current ''I'' (in amperes) can be calculated with the following equation: | |||
| Electric arcs, which can occur with supplies of any voltage (for example, a typical ] machine has a voltage between the electrodes of just a few volts), are very hot and emit ultra-violet and infra-red radiation. Proximity to an electric arc can therefore cause severe burns while UV is damaging to the unprotected eye. | |||
| <math display=block>I = {Q \over t} \, ,</math> | |||
| where ''Q'' is the electric charge transferred through the surface over a ] ''t''. If ''Q'' and ''t'' are measured in ]s and seconds respectively, ''I'' is in amperes. | |||
| More generally, electric current can be represented as the rate at which charge flows through a given surface as: | |||
| Accidental electric heating can also be dangerous. An overloaded power cable is a frequent cause of fire. A battery as small as an AA cell placed in a pocket with change can lead to a short circuit heating the battery and the coins which may inflict burns. NiCad and NiMh cells are particularly risky because they can deliver a very high current due to their low internal resistance. | |||
| <math display=block>I = \frac{\mathrm{d}Q}{\mathrm{d}t} \, .</math> | |||
| == |
===Electrolytes=== | ||
| {{Main|Conductivity (electrolytic)}} | |||
| ] in a static ].]] | |||
| Electric currents in ]s are flows of electrically charged particles (]s). For example, if an electric field is placed across a solution of ]<sup>+</sup> and ]<sup>−</sup> (and conditions are right) the sodium ions move towards the negative electrode (cathode), while the chloride ions move towards the positive electrode (anode). Reactions take place at both electrode surfaces, neutralizing each ion. | |||
| *] | |||
| *] | |||
| *] for more information on the physical mechanism of current flow in materials | |||
| *] | |||
| Water-ice and certain solid electrolytes called ]s contain positive hydrogen ions ("]s") that are mobile. In these materials, electric currents are composed of moving protons, as opposed to the moving electrons in metals. | |||
| ==External links== | |||
| In certain electrolyte mixtures, brightly coloured ions are the moving electric charges. The slow progress of the colour makes the current visible.<ref>{{cite book|first=Rudolf|last=Holze|url=https://books.google.com/books?id=TbcDvDcDFB0C&pg=PA44|title=Experimental Electrochemistry: A Laboratory Textbook|page=44|publisher=John Wiley & Sons|year=2009|isbn=978-3527310982}}</ref> | |||
| ===Gases and plasmas=== | |||
| In air and other ordinary ]es below the breakdown field, the dominant source of electrical conduction is via relatively few mobile ions produced by radioactive gases, ultraviolet light, or cosmic rays. Since the electrical conductivity is low, gases are ]s or ]. However, once the applied ] approaches the ] value, free electrons become sufficiently accelerated by the electric field to create additional free electrons by colliding, and ], neutral gas atoms or molecules in a process called ]. The breakdown process forms a ] that contains enough mobile electrons and positive ions to make it an electrical conductor. In the process, it forms a light emitting conductive path, such as a ], ] or ]. | |||
| ] is the state of matter where some of the electrons in a gas are stripped or "ionized" from their ]s or atoms. A plasma can be formed by high ], or by application of a high electric or alternating magnetic field as noted above. Due to their lower mass, the electrons in a plasma accelerate more quickly in response to an electric field than the heavier positive ions, and hence carry the bulk of the current. The free ions recombine to create new chemical compounds (for example, breaking atmospheric oxygen into single oxygen , which then recombine creating ] ).<ref>{{cite web | title = Lab Note #106 ''Environmental Impact of Arc Suppression'' | publisher = Arc Suppression Technologies | date = April 2011 | url = http://www.arcsuppressiontechnologies.com/arc-suppression-facts/lab-app-notes/ | access-date = March 15, 2012}}</ref> | |||
| ===Vacuum=== | |||
| Since a "]" contains no charged particles, it normally behaves as a perfect insulator. However, metal electrode surfaces can cause a region of the vacuum to become conductive by injecting free electrons or ]s through either ] or ]. Thermionic emission occurs when the thermal energy exceeds the metal's ], while ] occurs when the electric field at the surface of the metal is high enough to cause ], which results in the ejection of free electrons from the metal into the vacuum. Externally heated electrodes are often used to generate an ] as in the ] or indirectly ] of ]s. ] can also spontaneously produce electron clouds via thermionic emission when small incandescent regions (called ''cathode spots'' or ''anode spots'') are formed. These are incandescent regions of the electrode surface that are created by a localized high current. These regions may be initiated by ], but are then sustained by localized thermionic emission once a ] forms. These small electron-emitting regions can form quite rapidly, even explosively, on a metal surface subjected to a high electrical field. ]s and ] are some of the electronic switching and amplifying devices based on vacuum conductivity. | |||
| ===Superconductivity=== | |||
| {{Main|Superconductivity}} | |||
| Superconductivity is a phenomenon of exactly zero ] and expulsion of ]s occurring in certain materials when ] below a characteristic ]. It was discovered by ] on April 8, 1911 in ]. Like ] and ]s, superconductivity is a ] phenomenon. It is characterized by the ], the complete ejection of ] from the interior of the superconductor as it transitions into the superconducting state. The occurrence of the Meissner effect indicates that superconductivity cannot be understood simply as the idealization of '']'' in ]. | |||
| ===Semiconductor=== | |||
| {{Main|Semiconductor}} | |||
| In a ] it is sometimes useful to think of the current as due to the flow of positive "]" (the mobile positive charge carriers that are places where the semiconductor crystal is missing a valence electron). This is the case in a p-type semiconductor. A semiconductor has ] intermediate in magnitude between that of a ] and an ]. This means a conductivity roughly in the range of 10<sup>−2</sup> to 10<sup>4</sup> ] per centimeter (S⋅cm<sup>−1</sup>). | |||
| In the classic crystalline semiconductors, electrons can have energies only within certain bands (i.e. ranges of levels of energy). Energetically, these bands are located between the energy of the ground state, the state in which electrons are tightly bound to the atomic nuclei of the material, and the free electron energy, the latter describing the energy required for an electron to escape entirely from the material. The energy bands each correspond to many discrete ]s of the electrons, and most of the states with low energy (closer to the nucleus) are occupied, up to a particular band called the '']''. Semiconductors and insulators are distinguished from ] because the valence band in any given metal is nearly filled with electrons under usual operating conditions, while very few (semiconductor) or virtually none (insulator) of them are available in the ''conduction band'', the band immediately above the valence band. | |||
| The ease of exciting electrons in the semiconductor from the valence band to the conduction band depends on the ] between the bands. The size of this energy band gap serves as an arbitrary dividing line (roughly 4 ]) between semiconductors and ]. | |||
| With covalent bonds, an electron moves by hopping to a neighboring bond. The ] requires that the electron be lifted into the higher anti-bonding state of that bond. For delocalized states, for example in one dimension{{snd}}that is in a ], for every energy there is a state with electrons flowing in one direction and another state with the electrons flowing in the other. For a net current to flow, more states for one direction than for the other direction must be occupied. For this to occur, energy is required, as in the semiconductor the next higher states lie above the band gap. Often this is stated as: full bands do not contribute to the ]. However, as a semiconductor's temperature rises above ], there is more energy in the semiconductor to spend on lattice vibration and on exciting electrons into the conduction band. The current-carrying electrons in the conduction band are known as ''free electrons'', though they are often simply called ''electrons'' if that is clear in context. | |||
| ==Current density and Ohm's law== | |||
| {{Main|Current density}} | |||
| Current density is the rate at which charge passes through a chosen unit area.<ref name="Zangwill2013">{{cite book|first=Andrew |last=Zangwill|title=Modern Electrodynamics|year=2013|publisher=Cambridge University Press|isbn=978-0-521-89697-9}}</ref>{{rp|31}} It is defined as a ] whose magnitude is the current per unit cross-sectional area.<ref name=Walker/>{{rp|749}} As discussed in ], the direction is arbitrary. Conventionally, if the moving charges are positive, then the current density has the same sign as the velocity of the charges. For negative charges, the sign of the current density is opposite to the velocity of the charges.<ref name=Walker/>{{rp|749}} In ], current density (symbol: j) is expressed in the SI base units of amperes per square metre.<ref name="SI"/>{{rp|22}} | |||
| In linear materials such as metals, and under low frequencies, the current density across the conductor surface is uniform. In such conditions, ] states that the current is directly proportional to the potential difference between two ends (across) of that metal (ideal) ] (or other ]): | |||
| <math display=block>I = {V \over R} \, ,</math> | |||
| where <math>I</math> is the current, measured in amperes; <math>V</math> is the ], measured in ]s; and <math>R</math> is the ], measured in ]s. For ]s, especially at higher frequencies, ] causes the current to spread unevenly across the conductor cross-section, with higher density near the surface, thus increasing the apparent resistance. | |||
| ==Drift speed== | |||
| The mobile charged particles within a conductor move constantly in random directions, like the particles of a ]. (More accurately, a ].) To create a net flow of charge, the particles must also move together with an average drift rate. Electrons are the charge carriers in most ]s and they follow an erratic path, bouncing from atom to atom, but generally drifting in the opposite direction of the electric field. The speed they drift at can be calculated from the equation: | |||
| <math display=block>I=nAvQ \, ,</math> | |||
| where | |||
| * <math>I</math> is the electric current | |||
| * <math>n</math> is number of charged particles per unit volume (or charge carrier density) | |||
| * <math>A</math> is the cross-sectional area of the conductor | |||
| * <math>v</math> is the ], and | |||
| * <math>Q</math> is the charge on each particle. | |||
| Typically, electric charges in solids flow slowly. For example, in a ] wire of cross-section 0.5 mm<sup>2</sup>, carrying a current of 5 A, the ] of the electrons is on the order of a millimetre per second. To take a different example, in the near-vacuum inside a ], the electrons travel in near-straight lines at about a tenth of the ]. | |||
| Any accelerating electric charge, and therefore any changing electric current, gives rise to an ] wave that propagates at very high speed outside the surface of the conductor. This speed is usually a significant fraction of the speed of light, as can be deduced from ], and is therefore many times faster than the drift velocity of the electrons. For example, in ], the waves of electromagnetic energy propagate through the space between the wires, moving from a source to a distant ], even though the electrons in the wires only move back and forth over a tiny distance. | |||
| The ratio of the speed of the electromagnetic wave to the speed of light in free space is called the ], and depends on the electromagnetic properties of the conductor and the insulating materials surrounding it, and on their shape and size. | |||
| The magnitudes (not the natures) of these three velocities can be illustrated by an analogy with the three similar velocities associated with gases. (See also ].) | |||
| * The low drift velocity of charge carriers is analogous to air motion; in other words, winds. | |||
| * The high speed of electromagnetic waves is roughly analogous to the speed of sound in a gas (sound waves move through air much faster than large-scale motions such as ]) | |||
| * The random motion of charges is analogous to heat{{snd}}the thermal velocity of randomly vibrating gas particles. | |||
| ==See also== | |||
| {{Portal|Electronics}} | |||
| {{Wiktionary|amperage}} | |||
| {{div col}} | |||
| * ] | |||
| * ] (electric) and {{slink|Magnetic_current|Magnetic_displacement_current}} | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| {{div col end}} | |||
| ==Notes== | |||
| {{notelist}} | |||
| ==References== | |||
| * - convert selected unit to all other units of current | |||
| {{Reflist|30em}} | |||
| {{SI base quantities}} | |||
| * | |||
| {{Authority control}} | |||
| * - a useful site introducing electricity and electronics, as well as some mathematics involved with circuit calculations. | |||
| ] | |||
| ] | |||
| ] | |||
| {{DEFAULTSORT:Electric Current}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 15:07, 15 November 2024
Flow of electric charge
| Electric current | |
|---|---|
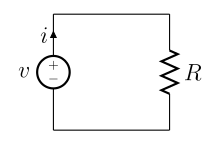 A simple electric circuit, where current is represented by the letter i. The relationship between the voltage (V), resistance (R), and current (i or I) is V=IR; this is known as Ohm's law. A simple electric circuit, where current is represented by the letter i. The relationship between the voltage (V), resistance (R), and current (i or I) is V=IR; this is known as Ohm's law. | |
| Common symbols | I |
| SI unit | ampere |
| Derivations from other quantities | |
| Dimension | |
An electric current is a flow of charged particles, such as electrons or ions, moving through an electrical conductor or space. It is defined as the net rate of flow of electric charge through a surface. The moving particles are called charge carriers, which may be one of several types of particles, depending on the conductor. In electric circuits the charge carriers are often electrons moving through a wire. In semiconductors they can be electrons or holes. In an electrolyte the charge carriers are ions, while in plasma, an ionized gas, they are ions and electrons.
In the International System of Units (SI), electric current is expressed in units of ampere (sometimes called an "amp", symbol A), which is equivalent to one coulomb per second. The ampere is an SI base unit and electric current is a base quantity in the International System of Quantities (ISQ). Electric current is also known as amperage and is measured using a device called an ammeter.
Electric currents create magnetic fields, which are used in motors, generators, inductors, and transformers. In ordinary conductors, they cause Joule heating, which creates light in incandescent light bulbs. Time-varying currents emit electromagnetic waves, which are used in telecommunications to broadcast information.
Symbol
The conventional symbol for current is I, which originates from the French phrase intensité du courant, (current intensity). Current intensity is often referred to simply as current. The I symbol was used by André-Marie Ampère, after whom the unit of electric current is named, in formulating Ampère's force law (1820). The notation travelled from France to Great Britain, where it became standard, although at least one journal did not change from using C to I until 1896.
Conventions


The conventional direction of current, also known as conventional current, is arbitrarily defined as the direction in which positive charges flow. In a conductive material, the moving charged particles that constitute the electric current are called charge carriers. In metals, which make up the wires and other conductors in most electrical circuits, the positively charged atomic nuclei of the atoms are held in a fixed position, and the negatively charged electrons are the charge carriers, free to move about in the metal. In other materials, notably the semiconductors, the charge carriers can be positive or negative, depending on the dopant used. Positive and negative charge carriers may even be present at the same time, as happens in an electrolyte in an electrochemical cell.
A flow of positive charges gives the same electric current, and has the same effect in a circuit, as an equal flow of negative charges in the opposite direction. Since current can be the flow of either positive or negative charges, or both, a convention is needed for the direction of current that is independent of the type of charge carriers. Negatively charged carriers, such as the electrons (the charge carriers in metal wires and many other electronic circuit components), therefore flow in the opposite direction of conventional current flow in an electrical circuit.
Reference direction
A current in a wire or circuit element can flow in either of two directions. When defining a variable to represent the current, the direction representing positive current must be specified, usually by an arrow on the circuit schematic diagram. This is called the reference direction of the current . When analyzing electrical circuits, the actual direction of current through a specific circuit element is usually unknown until the analysis is completed. Consequently, the reference directions of currents are often assigned arbitrarily. When the circuit is solved, a negative value for the current implies the actual direction of current through that circuit element is opposite that of the chosen reference direction.
Ohm's law
Main article: Ohm's lawOhm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points. Introducing the constant of proportionality, the resistance, one arrives at the usual mathematical equation that describes this relationship:
where I is the current through the conductor in units of amperes, V is the potential difference measured across the conductor in units of volts, and R is the resistance of the conductor in units of ohms. More specifically, Ohm's law states that the R in this relation is constant, independent of the current.
Alternating and direct current
See also: War of the currents
In alternating current (AC) systems, the movement of electric charge periodically reverses direction. AC is the form of electric power most commonly delivered to businesses and residences. The usual waveform of an AC power circuit is a sine wave, though certain applications use alternative waveforms, such as triangular or square waves. Audio and radio signals carried on electrical wires are also examples of alternating current. An important goal in these applications is recovery of information encoded (or modulated) onto the AC signal.
In contrast, direct current (DC) refers to a system in which the movement of electric charge in only one direction (sometimes called unidirectional flow). Direct current is produced by sources such as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Alternating current can also be converted to direct current through use of a rectifier. Direct current may flow in a conductor such as a wire, but can also flow through semiconductors, insulators, or even through a vacuum as in electron or ion beams. An old name for direct current was galvanic current.
Occurrences
Natural observable examples of electric current include lightning, static electric discharge, and the solar wind, the source of the polar auroras.
Man-made occurrences of electric current include the flow of conduction electrons in metal wires such as the overhead power lines that deliver electrical energy across long distances and the smaller wires within electrical and electronic equipment. Eddy currents are electric currents that occur in conductors exposed to changing magnetic fields. Similarly, electric currents occur, particularly in the surface, of conductors exposed to electromagnetic waves. When oscillating electric currents flow at the correct voltages within radio antennas, radio waves are generated.
In electronics, other forms of electric current include the flow of electrons through resistors or through the vacuum in a vacuum tube, the flow of ions inside a battery, and the flow of holes within metals and semiconductors.
A biological example of current is the flow of ions in neurons and nerves, responsible for both thought and sensory perception.
Measurement
Current can be measured using an ammeter.
Electric current can be directly measured with a galvanometer, but this method involves breaking the electrical circuit, which is sometimes inconvenient.
Current can also be measured without breaking the circuit by detecting the magnetic field associated with the current. Devices, at the circuit level, use various techniques to measure current:
- Shunt resistors
- Hall effect current sensor transducers
- Transformers (however DC cannot be measured)
- Magnetoresistive field sensors
- Rogowski coils
- Current clamps
Resistive heating
Main article: Joule heatingJoule heating, also known as ohmic heating and resistive heating, is the process of power dissipation by which the passage of an electric current through a conductor increases the internal energy of the conductor, converting thermodynamic work into heat. The phenomenon was first studied by James Prescott Joule in 1841. Joule immersed a length of wire in a fixed mass of water and measured the temperature rise due to a known current through the wire for a 30 minute period. By varying the current and the length of the wire he deduced that the heat produced was proportional to the square of the current multiplied by the electrical resistance of the wire.
This relationship is known as Joule's Law. The SI unit of energy was subsequently named the joule and given the symbol J. The commonly known SI unit of power, the watt (symbol: W), is equivalent to one joule per second.
Electromagnetism
Main article: ElectromagnetismElectromagnet
Main article: Electromagnet
In an electromagnet a coil of wires behaves like a magnet when an electric current flows through it. When the current is switched off, the coil loses its magnetism immediately. Electric current produces a magnetic field. The magnetic field can be visualized as a pattern of circular field lines surrounding the wire that persists as long as there is current.
Electromagnetic induction
Main article: Electromagnetic induction
Magnetic fields can also be used to make electric currents. When a changing magnetic field is applied to a conductor, an electromotive force (EMF) is induced, which starts an electric current, when there is a suitable path.
Radio waves
Main article: Radio waves Further information: Radio-frequency currentWhen an electric current flows in a suitably shaped conductor at radio frequencies, radio waves can be generated. These travel at the speed of light and can cause electric currents in distant conductors.
Conduction mechanisms in various media
Main articles: Electrical conductivity and Charge transport mechanismsIn metallic solids, electric charge flows by means of electrons, from lower to higher electrical potential. In other media, any stream of charged objects (ions, for example) may constitute an electric current. To provide a definition of current independent of the type of charge carriers, conventional current is defined as moving in the same direction as the positive charge flow. So, in metals where the charge carriers (electrons) are negative, conventional current is in the opposite direction to the overall electron movement. In conductors where the charge carriers are positive, conventional current is in the same direction as the charge carriers.
In a vacuum, a beam of ions or electrons may be formed. In other conductive materials, the electric current is due to the flow of both positively and negatively charged particles at the same time. In still others, the current is entirely due to positive charge flow. For example, the electric currents in electrolytes are flows of positively and negatively charged ions. In a common lead-acid electrochemical cell, electric currents are composed of positive hydronium ions flowing in one direction, and negative sulfate ions flowing in the other. Electric currents in sparks or plasma are flows of electrons as well as positive and negative ions. In ice and in certain solid electrolytes, the electric current is entirely composed of flowing ions.
Metals
In a metal, some of the outer electrons in each atom are not bound to the individual molecules as they are in molecular solids, or in full bands as they are in insulating materials, but are free to move within the metal lattice. These conduction electrons can serve as charge carriers, carrying a current. Metals are particularly conductive because there are many of these free electrons. With no external electric field applied, these electrons move about randomly due to thermal energy but, on average, there is zero net current within the metal. At room temperature, the average speed of these random motions is 10 metres per second. Given a surface through which a metal wire passes, electrons move in both directions across the surface at an equal rate. As George Gamow wrote in his popular science book, One, Two, Three...Infinity (1947), "The metallic substances differ from all other materials by the fact that the outer shells of their atoms are bound rather loosely, and often let one of their electrons go free. Thus the interior of a metal is filled up with a large number of unattached electrons that travel aimlessly around like a crowd of displaced persons. When a metal wire is subjected to electric force applied on its opposite ends, these free electrons rush in the direction of the force, thus forming what we call an electric current."
When a metal wire is connected across the two terminals of a DC voltage source such as a battery, the source places an electric field across the conductor. The moment contact is made, the free electrons of the conductor are forced to drift toward the positive terminal under the influence of this field. The free electrons are therefore the charge carrier in a typical solid conductor.
For a steady flow of charge through a surface, the current I (in amperes) can be calculated with the following equation: where Q is the electric charge transferred through the surface over a time t. If Q and t are measured in coulombs and seconds respectively, I is in amperes.
More generally, electric current can be represented as the rate at which charge flows through a given surface as:
Electrolytes
Main article: Conductivity (electrolytic)
Electric currents in electrolytes are flows of electrically charged particles (ions). For example, if an electric field is placed across a solution of Na and Cl (and conditions are right) the sodium ions move towards the negative electrode (cathode), while the chloride ions move towards the positive electrode (anode). Reactions take place at both electrode surfaces, neutralizing each ion.
Water-ice and certain solid electrolytes called proton conductors contain positive hydrogen ions ("protons") that are mobile. In these materials, electric currents are composed of moving protons, as opposed to the moving electrons in metals.
In certain electrolyte mixtures, brightly coloured ions are the moving electric charges. The slow progress of the colour makes the current visible.
Gases and plasmas
In air and other ordinary gases below the breakdown field, the dominant source of electrical conduction is via relatively few mobile ions produced by radioactive gases, ultraviolet light, or cosmic rays. Since the electrical conductivity is low, gases are dielectrics or insulators. However, once the applied electric field approaches the breakdown value, free electrons become sufficiently accelerated by the electric field to create additional free electrons by colliding, and ionizing, neutral gas atoms or molecules in a process called avalanche breakdown. The breakdown process forms a plasma that contains enough mobile electrons and positive ions to make it an electrical conductor. In the process, it forms a light emitting conductive path, such as a spark, arc or lightning.
Plasma is the state of matter where some of the electrons in a gas are stripped or "ionized" from their molecules or atoms. A plasma can be formed by high temperature, or by application of a high electric or alternating magnetic field as noted above. Due to their lower mass, the electrons in a plasma accelerate more quickly in response to an electric field than the heavier positive ions, and hence carry the bulk of the current. The free ions recombine to create new chemical compounds (for example, breaking atmospheric oxygen into single oxygen , which then recombine creating ozone ).
Vacuum
Since a "perfect vacuum" contains no charged particles, it normally behaves as a perfect insulator. However, metal electrode surfaces can cause a region of the vacuum to become conductive by injecting free electrons or ions through either field electron emission or thermionic emission. Thermionic emission occurs when the thermal energy exceeds the metal's work function, while field electron emission occurs when the electric field at the surface of the metal is high enough to cause tunneling, which results in the ejection of free electrons from the metal into the vacuum. Externally heated electrodes are often used to generate an electron cloud as in the filament or indirectly heated cathode of vacuum tubes. Cold electrodes can also spontaneously produce electron clouds via thermionic emission when small incandescent regions (called cathode spots or anode spots) are formed. These are incandescent regions of the electrode surface that are created by a localized high current. These regions may be initiated by field electron emission, but are then sustained by localized thermionic emission once a vacuum arc forms. These small electron-emitting regions can form quite rapidly, even explosively, on a metal surface subjected to a high electrical field. Vacuum tubes and sprytrons are some of the electronic switching and amplifying devices based on vacuum conductivity.
Superconductivity
Main article: SuperconductivitySuperconductivity is a phenomenon of exactly zero electrical resistance and expulsion of magnetic fields occurring in certain materials when cooled below a characteristic critical temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum mechanical phenomenon. It is characterized by the Meissner effect, the complete ejection of magnetic field lines from the interior of the superconductor as it transitions into the superconducting state. The occurrence of the Meissner effect indicates that superconductivity cannot be understood simply as the idealization of perfect conductivity in classical physics.
Semiconductor
Main article: SemiconductorIn a semiconductor it is sometimes useful to think of the current as due to the flow of positive "holes" (the mobile positive charge carriers that are places where the semiconductor crystal is missing a valence electron). This is the case in a p-type semiconductor. A semiconductor has electrical conductivity intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 10 to 10 siemens per centimeter (S⋅cm).
In the classic crystalline semiconductors, electrons can have energies only within certain bands (i.e. ranges of levels of energy). Energetically, these bands are located between the energy of the ground state, the state in which electrons are tightly bound to the atomic nuclei of the material, and the free electron energy, the latter describing the energy required for an electron to escape entirely from the material. The energy bands each correspond to many discrete quantum states of the electrons, and most of the states with low energy (closer to the nucleus) are occupied, up to a particular band called the valence band. Semiconductors and insulators are distinguished from metals because the valence band in any given metal is nearly filled with electrons under usual operating conditions, while very few (semiconductor) or virtually none (insulator) of them are available in the conduction band, the band immediately above the valence band.
The ease of exciting electrons in the semiconductor from the valence band to the conduction band depends on the band gap between the bands. The size of this energy band gap serves as an arbitrary dividing line (roughly 4 eV) between semiconductors and insulators.
With covalent bonds, an electron moves by hopping to a neighboring bond. The Pauli exclusion principle requires that the electron be lifted into the higher anti-bonding state of that bond. For delocalized states, for example in one dimension – that is in a nanowire, for every energy there is a state with electrons flowing in one direction and another state with the electrons flowing in the other. For a net current to flow, more states for one direction than for the other direction must be occupied. For this to occur, energy is required, as in the semiconductor the next higher states lie above the band gap. Often this is stated as: full bands do not contribute to the electrical conductivity. However, as a semiconductor's temperature rises above absolute zero, there is more energy in the semiconductor to spend on lattice vibration and on exciting electrons into the conduction band. The current-carrying electrons in the conduction band are known as free electrons, though they are often simply called electrons if that is clear in context.
Current density and Ohm's law
Main article: Current densityCurrent density is the rate at which charge passes through a chosen unit area. It is defined as a vector whose magnitude is the current per unit cross-sectional area. As discussed in Reference direction, the direction is arbitrary. Conventionally, if the moving charges are positive, then the current density has the same sign as the velocity of the charges. For negative charges, the sign of the current density is opposite to the velocity of the charges. In SI units, current density (symbol: j) is expressed in the SI base units of amperes per square metre.
In linear materials such as metals, and under low frequencies, the current density across the conductor surface is uniform. In such conditions, Ohm's law states that the current is directly proportional to the potential difference between two ends (across) of that metal (ideal) resistor (or other ohmic device):
where is the current, measured in amperes; is the potential difference, measured in volts; and is the resistance, measured in ohms. For alternating currents, especially at higher frequencies, skin effect causes the current to spread unevenly across the conductor cross-section, with higher density near the surface, thus increasing the apparent resistance.
Drift speed
The mobile charged particles within a conductor move constantly in random directions, like the particles of a gas. (More accurately, a Fermi gas.) To create a net flow of charge, the particles must also move together with an average drift rate. Electrons are the charge carriers in most metals and they follow an erratic path, bouncing from atom to atom, but generally drifting in the opposite direction of the electric field. The speed they drift at can be calculated from the equation: where
- is the electric current
- is number of charged particles per unit volume (or charge carrier density)
- is the cross-sectional area of the conductor
- is the drift velocity, and
- is the charge on each particle.
Typically, electric charges in solids flow slowly. For example, in a copper wire of cross-section 0.5 mm, carrying a current of 5 A, the drift velocity of the electrons is on the order of a millimetre per second. To take a different example, in the near-vacuum inside a cathode-ray tube, the electrons travel in near-straight lines at about a tenth of the speed of light.
Any accelerating electric charge, and therefore any changing electric current, gives rise to an electromagnetic wave that propagates at very high speed outside the surface of the conductor. This speed is usually a significant fraction of the speed of light, as can be deduced from Maxwell's equations, and is therefore many times faster than the drift velocity of the electrons. For example, in AC power lines, the waves of electromagnetic energy propagate through the space between the wires, moving from a source to a distant load, even though the electrons in the wires only move back and forth over a tiny distance.
The ratio of the speed of the electromagnetic wave to the speed of light in free space is called the velocity factor, and depends on the electromagnetic properties of the conductor and the insulating materials surrounding it, and on their shape and size.
The magnitudes (not the natures) of these three velocities can be illustrated by an analogy with the three similar velocities associated with gases. (See also hydraulic analogy.)
- The low drift velocity of charge carriers is analogous to air motion; in other words, winds.
- The high speed of electromagnetic waves is roughly analogous to the speed of sound in a gas (sound waves move through air much faster than large-scale motions such as convection)
- The random motion of charges is analogous to heat – the thermal velocity of randomly vibrating gas particles.
See also
- Current density
- Displacement current (electric) and Magnetic current § Magnetic displacement current
- Electric shock
- Electrical measurements
- History of electrical engineering
- Polarity symbols
- International System of Quantities
- SI electromagnetism units
- Single-phase electric power
- Static electricity
- Three-phase electric power
- Two-phase electric power
Notes
- Our first step in the analysis is the assumption of reference directions for the unknown currents.
References
- Horowitz, Paul; Hill, Winfield (2015). The art of electronics (3rd ed.). Cambridge University Press. ISBN 978-0-521-80926-9.
- ^ Walker, Jearl; Halliday, David; Resnick, Robert (2014). Fundamentals of physics (10th ed.). Hoboken, NJ: Wiley. ISBN 978-1118230732. OCLC 950235056.
- Anthony C. Fischer-Cripps (2004). The electronics companion. CRC Press. p. 13. ISBN 978-0-7503-1012-3.
- ^ The International System of Units (PDF) (9th ed.), International Bureau of Weights and Measures, Dec 2022, ISBN 978-92-822-2272-0
- Lowe, T. L.; Rounce, John (2002). Calculations for A-level Physics. Nelson Thornes. p. 2. ISBN 0748767487.
- Berlin, Howard M.; Getz, Frank C. (1988). Principles of Electronic Instrumentation and Measurement. Merrill Pub. Co. p. 37. ISBN 0675204496.
- Kumar, K. S. Suresh (2013). "Section 1.2.3". Electric Circuit Analysis. Pearson Education India. ISBN 978-9332514102.
'Current intensity' is usually referred to as 'current' itself.
- Ampère, A-M (1822). "Recueil d'Observations Électro-dynamiques" (PDF) (in French). Paris: Chez Crochard Libraire. p. 56. Archived (PDF) from the original on 2011-07-24.
- Electric Power. Vol. 6. 1894. pp. 411, 1894.
- ^ Avison, John (2014). The World of Physics. Thomas Nelson and Sons. p. 221. ISBN 9780174387336.
- ^ McComb, Gordon; Boysen, Earl (2005). Electronics For Dummies. Wiley. p. 12. ISBN 9780764597190.
- Kumar, K. S. Suresh (2008). Electric Circuits & Networks. Pearson Education India. pp. 26–28. ISBN 978-8131713907.
- ^ Hayt, William (1989). Engineering Electromagnetics (5th ed.). McGraw-Hill. ISBN 0070274061.
- Consoliver, Earl L.; Mitchell, Grover I. (1920). Automotive ignition systems. McGraw-Hill. p. 4.
ohm's law current proportional voltage resistance.
- Robert A. Millikan and E. S. Bishop (1917). Elements of Electricity. American Technical Society. p. 54.
Ohm's law current directly proportional.
- Oliver Heaviside (1894). Electrical papers. Vol. 1. Macmillan and Co. p. 283. ISBN 978-0-8218-2840-3.
- Andrew J. Robinson; Lynn Snyder-Mackler (2007). Clinical Electrophysiology: Electrotherapy and Electrophysiologic Testing (3rd ed.). Lippincott Williams & Wilkins. p. 10. ISBN 978-0-7817-4484-3.
- "What is a Current Sensor and How is it Used?". Retrieved 2011-12-22.
- Friedrich, Andreas P.; Lemme, Helmuth (2000-05-01). "The Universal Current Sensor". Fierce Electronics. Archived from the original on 2016-03-04. Retrieved 2011-12-22.
- ^ Jaffe, Robert L.; Taylor, Washington (2018). The physics of energy. Cambridge University Press.
- ^ Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Thomson Brooks/Cole. ISBN 0-534-40842-7.
- "The Mechanism Of Conduction In Metals". Think Quest. Archived from the original on 2012-10-25.
- Holze, Rudolf (2009). Experimental Electrochemistry: A Laboratory Textbook. John Wiley & Sons. p. 44. ISBN 978-3527310982.
- "Lab Note #106 Environmental Impact of Arc Suppression". Arc Suppression Technologies. April 2011. Retrieved March 15, 2012.
- Zangwill, Andrew (2013). Modern Electrodynamics. Cambridge University Press. ISBN 978-0-521-89697-9.
| SI base quantities | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base quantities |
|  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| See also | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 to represent the current, the direction representing positive current must be specified, usually by an arrow on the
to represent the current, the direction representing positive current must be specified, usually by an arrow on the 

 where Q is the electric charge transferred through the surface over a
where Q is the electric charge transferred through the surface over a 

 is the
is the  is the
is the  where
where
 is number of charged particles per unit volume (or charge carrier density)
is number of charged particles per unit volume (or charge carrier density) is the cross-sectional area of the conductor
is the cross-sectional area of the conductor is the
is the  is the charge on each particle.
is the charge on each particle.