| Revision as of 13:10, 11 July 2013 editJNrgbKLM (talk | contribs)47 edits →The relation of colour charge to electric charge for fermions← Previous edit | Latest revision as of 02:49, 20 January 2025 edit undoOAbot (talk | contribs)Bots442,978 editsm Open access bot: arxiv updated in citation with #oabot. | ||
| (858 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Theory of forces and subatomic particles}} | |||
| {{about|the Standard Model of particle physics|other uses|Standard model (disambiguation)}} | |||
| {{About|a non-mathematical general overview of the Standard Model of particle physics|a mathematical description|Mathematical formulation of the Standard Model|other uses|Standard model (disambiguation)}} | |||
| {{Use dmy dates|date=September 2020}} | |||
| ]s, with the three ], ]s in the fourth column and the ] in the fifth.]] | |||
| {{Standard model of particle physics}} | {{Standard model of particle physics}} | ||
| The '''Standard Model''' of ] is the ] describing three of the four known ]s (], ] and ]s – excluding ]) in the ] and classifying all known ]s. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide,<ref> | |||
| The '''Standard Model''' of ] is a theory concerning the ], ], and ] nuclear interactions, which mediate the dynamics of the known subatomic ]s. It was developed throughout the latter half of the 20th century, as a collaborative effort of scientists around the world.<ref>Oerter, Robert (2006-09-26). The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics (p. 2). Penguin Group. Kindle Edition.</ref> The current formulation was finalized in the mid-1970s upon experimental confirmation of the existence of ]s. Since then, discoveries of the ] (1977), the ] (1995), and the ] (2000) have given further credence to the Standard Model. More recently (2011–2012), the possible detection of the ] would complete the set of predicted particles upon its verification. Because of its success in explaining a wide variety of experimental results, the Standard Model is sometimes regarded as a "theory of almost everything". | |||
| {{cite book |author=R. Oerter |url=https://archive.org/details/theoryofalmostev0000oert |title=The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics |publisher=] |year=2006 |isbn=978-0-13-236678-6 |edition=Kindle |page= |access-date=28 March 2022 |url-access=registration}} {{Dead link |date=March 2022}}</ref> with the current formulation being finalized in the mid-1970s upon ] of the existence of ]s. Since then, proof of the ] (1995), the ] (2000), and the ] (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of ]s and the ] with great accuracy. | |||
| Although the Standard Model is believed to be theoretically self-consistent{{notetag|There are mathematical issues regarding quantum field theories still under debate (see e.g. ]), but the predictions extracted from the Standard Model by current methods applicable to current experiments are all self-consistent.<ref>{{cite book|chapter=25 |author=R. Mann |title=An Introduction to Particle Physics and the Standard Model |publisher=] |year=2010 |isbn=978-1-4200-8298-2}}</ref>}} and has demonstrated some success in providing ]s, it leaves some ] and so falls short of being a ].<ref name="NYT-20230911">{{cite news |last=Overbye |first=Dennis |author-link=Dennis Overbye |date=11 September 2023 |title=Don't Expect a 'Theory of Everything' to Explain It All |url=https://www.nytimes.com/2023/09/11/science/space/astronomy-universe-simulations.html |url-access=limited |url-status=live |archiveurl=https://archive.today/20230911043212/https://www.nytimes.com/2023/09/11/science/space/astronomy-universe-simulations.html |archivedate=11 September 2023 |accessdate=11 September 2023 |work=]}}</ref> For example, it does not fully explain ], incorporate the full ]<ref>{{Cite book|isbn=978-1-59803-350-2 |oclc=288435552 |last1=Carroll |first1=Sean M. |url=https://www.worldcat.org/oclc/288435552 |title=Dark Matter, Dark Energy: The Dark Side of the Universe |last2=Rhoades |first2=Zachary H. |last3=Leven |first3=Jon |publisher=] |year=2007 |series=Guidebook Part 2 |location=Chantilly, VA |pages=59 |quote=...Standard Model of Particle Physics: The modern theory of elementary particles and their interactions ... It does not, strictly speaking, include gravity, although it's often convenient to include gravitons among the known particles of nature... |access-date=28 March 2022}}</ref> as described by ], or account for the ] as possibly described by ]. The model does not contain any viable ] particle that possesses all of the required properties deduced from observational ]. It also does not incorporate ]s and their non-zero masses. | |||
| The Standard Model falls short of being a ] because it makes certain simplifying ]. It does not incorporate the full theory of ] as described by ], or predict the accelerating expansion of the universe (as possibly described by ]). The theory does not contain any viable ] particle that possesses all of the required properties deduced from observational ]. It also does not correctly account for ]s (and their non-zero masses). Although the Standard Model is believed to be theoretically self-consistent<ref>In fact, there are mathematical issues regarding quantum field theories still under debate (see e.g. ]), but the predictions extracted from the Standard Model by current methods are all self-consistent. For a further discussion see e.g. Chapter 25 of ''An Introduction to Particle Physics and the Standard Model'', by R. Mann (CRC Press, 2010) ISBN 978-1420082982</ref> and has demonstrated huge and continued successes in providing experimental predictions, it does leave some ]. | |||
| The development of the Standard Model was driven by ] and ] particle physicists alike. |
The development of the Standard Model was driven by ] and ] particle physicists alike. The Standard Model is a paradigm of a ] for theorists, exhibiting a wide range of phenomena, including ], ], and non-perturbative behavior. It is used as a basis for building more exotic models that incorporate ]s, ], and elaborate symmetries (such as ]) to explain experimental results at variance with the Standard Model, such as the existence of dark matter and neutrino oscillations. | ||
| ==Historical background== | == Historical background == | ||
| {{See also|History of quantum field theory|History of subatomic physics|Julian Schwinger|John Clive Ward}} | |||
| The first step towards the Standard Model was ]'s discovery in 1960 of a way to combine the ] and ]s.<ref> | |||
| In 1928, ] introduced the ], which implied the existence of ]. | |||
| In 1954, ] and ] extended the concept of ] for ]s, e.g. ], to ]s to provide an explanation for ]s.<ref name="YM">{{cite journal |author-link1=Chen-Ning Yang |first1=C. N. |last1=Yang |author-link2=Robert Mills (physicist) |first2=R. |last2=Mills |title=Conservation of Isotopic Spin and Isotopic Gauge Invariance |journal=] |volume=96 |issue=1 |pages=191–195 |year=1954 |doi=10.1103/PhysRev.96.191|bibcode = 1954PhRv...96..191Y |doi-access=free }}</ref> In 1957, ] demonstrated ] was not conserved in the ].<ref>{{cite web|last=Cho|first=Adrian|title=Postage stamp to honor female physicist who many say should have won the Nobel Prize|date=5 February 2021|url=https://www.science.org/content/article/postage-stamp-honor-female-physicist-who-many-say-should-have-won-nobel-prize}}</ref> | |||
| In 1961, ] combined the ] and ]s.<ref> | |||
| {{cite journal | {{cite journal | ||
| | |
|author=S.L. Glashow | ||
| | |
|year=1961 | ||
| | |
|title=Partial-symmetries of weak interactions | ||
| | |
|journal=] | ||
| | |
|volume=22 |issue=4 |pages=579–588 | ||
| |bibcode=1961NucPh..22..579G | |||
| | doi=10.1016/0029-5582(61)90469-2 | |||
| |doi=10.1016/0029-5582(61)90469-2 | |||
| |bibcode = 1961NucPh..22..579G | |||
| }}</ref> In 1964, Murray Gell-Mann and George Zweig introduced quarks and that same year ] implicitly introduced color charge of quarks.<ref>{{Citation |last=Greenberg |first=Oscar Wallace |title=Color Charge Degree of Freedom in Particle Physics |date=2009 |work=Compendium of Quantum Physics |pages=109–111 |editor-last=Greenberger |editor-first=Daniel |url=https://link.springer.com/chapter/10.1007/978-3-540-70626-7_32 |access-date=2024-09-17 |place=Berlin, Heidelberg |publisher=Springer |language=en |doi=10.1007/978-3-540-70626-7_32 |isbn=978-3-540-70626-7 |editor2-last=Hentschel |editor2-first=Klaus |editor3-last=Weinert |editor3-first=Friedel}}</ref> In 1967 ]<ref> | |||
| | issue=4 }}</ref> In 1967 ]<ref> | |||
| {{cite journal | {{cite journal | ||
| | |
|author=S. Weinberg | ||
| | |
|year=1967 | ||
| | |
|title=A Model of Leptons | ||
| | |
|journal=] | ||
| | |
|volume=19 |issue=21 |pages=1264–1266 | ||
| |bibcode=1967PhRvL..19.1264W | |||
| | doi=10.1103/PhysRevLett.19.1264 | |||
| |doi=10.1103/PhysRevLett.19.1264 | |||
| | bibcode=1967PhRvL..19.1264W | |||
| |doi-access=free | |||
| | issue=21 | |||
| }}</ref> and ]<ref> | }}</ref> and ]<ref> | ||
| {{cite conference | {{cite conference | ||
| | |
|author=A. Salam | ||
| | |
|editor=N. Svartholm | ||
| | |
|year=1968 | ||
| | |
|book-title=Elementary Particle Physics: Relativistic Groups and Analyticity | ||
| | |
|pages=367 | ||
| | |
|conference=Eighth Nobel Symposium | ||
| | |
|publisher=Almquvist and Wiksell | ||
| | |
|location=Stockholm | ||
| }}</ref> incorporated the ]<ref> | }}</ref> incorporated the ]<ref name="Englert1964"> | ||
| {{cite journal | {{cite journal | ||
| | |
|author1=F. Englert |author2=R. Brout |year=1964 | ||
| |title=Broken Symmetry and the Mass of Gauge Vector Mesons | |||
| | year=1964 | |||
| |journal=] | |||
| | title=Broken Symmetry and the Mass of Gauge Vector Mesons | |||
| |volume=13 |issue=9 |pages=321–323 | |||
| | journal=] | |||
| |bibcode=1964PhRvL..13..321E | |||
| | volume=13 | pages=321–323 | |||
| | |
|doi=10.1103/PhysRevLett.13.321 | ||
| |doi-access=free}}</ref><ref name="Peter W. Higgs 1964 508–509"> | |||
| | bibcode=1964PhRvL..13..321E | |||
| {{cite journal |author=P.W. Higgs |year=1964 |title=Broken Symmetries and the Masses of Gauge Bosons |journal=] |volume=13 |issue=16 |pages=508–509 |bibcode=1964PhRvL..13..508H |doi=10.1103/PhysRevLett.13.508 |doi-access=free}}</ref><ref name="G.S. Guralnik, C.R. Hagen, T.W.B. Kibble 1964 585–587"> | |||
| | issue=9 | |||
| }}</ref><ref> | |||
| {{cite journal | |||
| | author=P.W. Higgs | |||
| | year=1964 | |||
| | title=Broken Symmetries and the Masses of Gauge Bosons | |||
| | journal=] | |||
| | volume=13 | pages=508–509 | |||
| | doi=10.1103/PhysRevLett.13.508 | |||
| | bibcode=1964PhRvL..13..508H | |||
| | issue=16 | |||
| }}</ref><ref> | |||
| {{cite journal | {{cite journal | ||
| | |
|author1=G.S. Guralnik |author2=C.R. Hagen |author3=T.W.B. Kibble |year=1964 | ||
| |title=Global Conservation Laws and Massless Particles | |||
| | year=1964 | |||
| |journal=] | |||
| | title=Global Conservation Laws and Massless Particles | |||
| |volume=13 |issue=20 |pages=585–587 | |||
| | journal=] | |||
| |bibcode=1964PhRvL..13..585G | |||
| | volume=13 | pages=585–587 | |||
| | |
|doi=10.1103/PhysRevLett.13.585 | ||
| |doi-access=free}}</ref> into Glashow's ], giving it its modern form. | |||
| | bibcode=1964PhRvL..13..585G | |||
| | issue=20 | |||
| In 1970, Sheldon Glashow, John Iliopoulos, and Luciano Maiani introduced the ], predicting the ].<ref name=":2">{{Cite journal |last=Weinberg |first=S. |date=2004-05-01 |title=The making of the Standard Model |url=https://link.springer.com/article/10.1140/epjc/s2004-01761-1 |journal=European Physical Journal C |language=en |volume=34 |issue=1 |pages=5–13 |doi=10.1140/epjc/s2004-01761-1 |arxiv=hep-ph/0401010 |bibcode=2004EPJC...34....5W |issn=1434-6052}}</ref> In 1973 Gross and Wilczek and Politzer independently discovered that non-Abelian gauge theories, like the color theory of the strong force, have ].<ref name=":2" /> In 1976, Martin Perl discovered the ] at the ].<ref>{{Cite web |title=The Nobel Prize in Physics 1995 |url=https://www.nobelprize.org/prizes/physics/1995/perl/facts/#:~:text=In%20a%20series%20of%20experiments,alongside%20two%20previously%20known%20families. |access-date=2024-09-17 |website=NobelPrize.org |language=en-US}}</ref><ref>{{Cite web |last=magazine |first=STANFORD |date=2015-01-01 |title=In Memoriam |url=https://stanfordmag.org/contents/in-memoriam |access-date=2024-09-17 |website=stanfordmag.org |language=en}}</ref> In 1977, a team led by Leon Lederman at Fermilab discovered the bottom quark.<ref>{{Cite web |title=Inquiring Minds {{!}} Discoveries at Fermilab - The Bottom Quark |url=https://www.fnal.gov/pub/inquiring/physics/discoveries/bottom_quark.html |access-date=2024-09-17 |website=www.fnal.gov}}</ref> | |||
| }}</ref> into Glashow's ], giving it its modern form. | |||
| The Higgs mechanism is believed to give rise to the ]es of all the ]s in the Standard Model. This includes |
The Higgs mechanism is believed to give rise to the ]es of all the ]s in the Standard Model. This includes the masses of the ], and the masses of the ]s, i.e. the ]s and ]s. | ||
| After the ] caused by ] |
After the ] caused by ] exchange ] at ] in 1973,<ref> | ||
| {{cite journal | {{cite journal | ||
| |author=F.J. Hasert |
|author=F.J. Hasert |display-authors=etal | ||
| |year=1973 | |year=1973 | ||
| |title=Search for elastic muon-neutrino electron scattering | |title=Search for elastic muon-neutrino electron scattering | ||
| |journal=] | |journal=] | ||
| |volume=46 |page=121 | |volume=46 |issue=1 |page=121 | ||
| |bibcode=1973PhLB...46..121H | |||
| |doi=10.1016/0370-2693(73)90494-2 | |doi=10.1016/0370-2693(73)90494-2 | ||
| }}</ref><ref> | |||
| |bibcode = 1973PhLB...46..121H | |||
| |last2=Faissner | |||
| |first2=H. | |||
| |last3=Krenz | |||
| |first3=W. | |||
| |last4=Von Krogh | |||
| |first4=J. | |||
| |last5=Lanske | |||
| |first5=D. | |||
| |last6=Morfin | |||
| |first6=J. | |||
| |last7=Schultze | |||
| |first7=K. | |||
| |last8=Weerts | |||
| |first8=H. | |||
| |last9=Bertrand-Coremans | |||
| |first9=G.H. }}</ref><ref> | |||
| {{cite journal | {{cite journal | ||
| |author=F.J. Hasert |
|author=F.J. Hasert |display-authors=etal | ||
| |year=1973 | |year=1973 | ||
| |title=Observation of neutrino-like interactions without muon or electron in the |
|title=Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment | ||
| |journal=] | |journal=] | ||
| |volume=46 |page=138 | |volume=46 |issue=1 |page=138 | ||
| |bibcode=1973PhLB...46..138H | |||
| |doi=10.1016/0370-2693(73)90499-1 | |doi=10.1016/0370-2693(73)90499-1 | ||
| }}</ref><ref> | |||
| |bibcode = 1973PhLB...46..138H | |||
| |last2=Kabe | |||
| |first2=S. | |||
| |last3=Krenz | |||
| |first3=W. | |||
| |last4=Von Krogh | |||
| |first4=J. | |||
| |last5=Lanske | |||
| |first5=D. | |||
| |last6=Morfin | |||
| |first6=J. | |||
| |last7=Schultze | |||
| |first7=K. | |||
| |last8=Weerts | |||
| |first8=H. | |||
| |last9=Bertrand-Coremans | |||
| |first9=G.H. }}</ref><ref> | |||
| {{cite journal | {{cite journal | ||
| |author=F.J. Hasert |
|author=F.J. Hasert | ||
| |year=1974 | |year=1974 | ||
| |title=Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment | |title=Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment | ||
| |journal=] | |journal=] | ||
| |volume=73 |page=1 | |volume=73 |issue=1 |page=1 | ||
| |bibcode=1974NuPhB..73....1H | |||
| |doi=10.1016/0550-3213(74)90038-8 | |doi=10.1016/0550-3213(74)90038-8 | ||
| |display-authors=etal}}</ref><ref>{{cite web | |||
| |bibcode = 1974NuPhB..73....1H | |||
| |last2=Kabe | |||
| |first2=S. | |||
| |last3=Krenz | |||
| |first3=W. | |||
| |last4=Von Krogh | |||
| |first4=J. | |||
| |last5=Lanske | |||
| |first5=D. | |||
| |last6=Morfin | |||
| |first6=J. | |||
| |last7=Schultze | |||
| |first7=K. | |||
| |last8=Weerts | |||
| |first8=H. | |||
| |last9=Bertrand-Coremans | |||
| |first9=G. }}</ref><ref> | |||
| {{cite web | |||
| |author=D. Haidt | |author=D. Haidt | ||
| |date=4 October 2004 | |date=4 October 2004 | ||
| Line 153: | Line 102: | ||
| |url=http://cerncourier.com/cws/article/cern/29168 | |url=http://cerncourier.com/cws/article/cern/29168 | ||
| |work=] | |work=] | ||
| | |
|access-date=8 May 2008 | ||
| |archive-date=20 May 2011 | |||
| }}</ref> the electroweak theory became widely accepted and Glashow, Salam, and Weinberg shared the 1979 ] for discovering it. The W and Z ]s were discovered experimentally in 1981, and their masses were found to be as the Standard Model predicted. | |||
| |archive-url=https://web.archive.org/web/20110520115858/http://cerncourier.com/cws/article/cern/29168 | |||
| |url-status=dead | |||
| }}</ref> the electroweak theory became widely accepted and Glashow, Salam, and Weinberg shared the 1979 ] for discovering it. The W<sup>±</sup> and Z<sup>0</sup> ]s were discovered experimentally in 1983; and the ratio of their masses was found to be as the Standard Model predicted.<ref>{{cite journal|last1=Gaillard|first1=Mary K.|author-link1=Mary K. Gaillard|last2=Grannis|first2= Paul D. |last3=Sciulli|first3=Frank J.|title=The Standard Model of Particle Physics|date=January 1999|journal=Reviews of Modern Physics|doi=10.1103/RevModPhys.71.S96|volume=71|issue=2 |pages=S96–S111|arxiv=hep-ph/9812285|bibcode=1999RvMPS..71...96G|s2cid=119012610}}</ref> | |||
| The theory of the ], to which many contributed, acquired its modern form |
The theory of the ] (i.e. ], QCD), to which many contributed, acquired its modern form in 1973–74 when ] was proposed<ref> | ||
| {{cite journal | |||
| |author1=D.J. Gross |author2=F. Wilczek |year=1973 | |||
| |title=Ultraviolet behavior of non-abelian gauge theories | |||
| |journal=] | |||
| |volume=30 |issue= 26|pages= 1343–1346 | |||
| |bibcode=1973PhRvL..30.1343G | |||
| |doi=10.1103/PhysRevLett.30.1343 | |||
| |doi-access=free}}</ref><ref> | |||
| {{cite journal | |||
| |author=H.D. Politzer | |||
| |year=1973 | |||
| |title=Reliable perturbative results for strong interactions | |||
| |journal=] | |||
| |volume=30 |issue=26 |pages=1346–1349 | |||
| |bibcode=1973PhRvL..30.1346P | |||
| |doi=10.1103/PhysRevLett.30.1346 | |||
| |url=https://authors.library.caltech.edu/6668/1/POLprl73.pdf |archive-url=https://web.archive.org/web/20180719010018/https://authors.library.caltech.edu/6668/1/POLprl73.pdf |archive-date=2018-07-19 |url-status=live | |||
| |doi-access=free | |||
| }}</ref> (a development that made QCD the main focus of theoretical research)<ref>] (2014). ''A Brief History of String Theory: From Dual Models to M-Theory''. Springer, p. 11 n. 22.</ref> and experiments confirmed that the ]s were composed of fractionally charged quarks.<ref> | |||
| {{cite journal | |||
| |last1=Aubert |first1=J. | |||
| |year=1974 | |||
| |title=Experimental Observation of a Heavy Particle J | |||
| |journal=] | |||
| |volume=33 |issue=23 |pages=1404–1406 | |||
| |bibcode = 1974PhRvL..33.1404A | |||
| |doi=10.1103/PhysRevLett.33.1404 | |||
| |display-authors=etal|doi-access=free | |||
| }}</ref><ref> | |||
| {{cite journal | |||
| |last1=Augustin |first1=J. | |||
| |year=1974 | |||
| |title=Discovery of a Narrow Resonance in e<sup>+</sup>e<sup>−</sup> Annihilation | |||
| |journal=] | |||
| |volume=33 |issue=23 |pages=1406–1408 | |||
| |bibcode = 1974PhRvL..33.1406A | |||
| |doi=10.1103/PhysRevLett.33.1406 | |||
| |display-authors=etal|doi-access=free | |||
| }}</ref> | |||
| The term "Standard Model" was introduced by ] and ] in 1975,<ref> | |||
| ==Overview== | |||
| {{cite journal |last1=Pais |first1=A. |last2=Treiman |first2=S. B. |year=1975 |title=How Many Charm Quantum Numbers are There? |journal=] |volume=35 |issue=23 |pages=1556–1559 |doi=10.1103/PhysRevLett.35.1556 |bibcode=1975PhRvL..35.1556P |doi-access=}}</ref> with reference to the electroweak theory with four quarks.<ref>{{Cite book |last=Cao |first=Tian Yu |url=http://dx.doi.org/10.1017/9781108566926 |title=Conceptual Developments of 20th Century Field Theories |date=1 October 2019 |publisher=Cambridge University Press |isbn=978-1-108-56692-6 |publication-date=1998 |page=320|doi=10.1017/9781108566926 |bibcode=2019code.book.....C |s2cid=243686857 }}</ref> ], has since claimed priority, explaining that he chose the term Standard ] out of a sense of modesty<ref>A ] is a representation of reality, whereas a ] is an explanation of reality; this Misplaced Pages article and some of the literature refers to the Standard Model as a theory.</ref><ref>{{Cite web |last=Weinberg |first=Steven |title=This World and the Universe |url=https://www.youtube.com/watch?v=Gnk0rnBQrR0&t=1080s |access-date=29 March 2022 |website=] |date=20 April 2010 |publisher=Talks at Google}}</ref><ref>{{Cite web |year=2015 |title=World Science Festival |url=https://www.youtube.com/watch?v=g-y3DPJRVhE&t=435s |access-date=29 March 2022 |website=]}}</ref>{{Better source needed|reason=The current source is insufficiently reliable (]).|date=March 2022}} and used it in 1973 during a talk in Aix-en-Provence in France.<ref>{{cite web| url = https://www.aps.org/publications/apsnews/201902/weinberg.cfm| title = Q&A with Standard Bearer Steven Weinberg}}</ref> | |||
| At present, ] and ] are best understood in terms of the ] and ] of elementary particles. To date, physics has reduced the ] governing the behavior and interaction of all known forms of matter and energy to a small set of fundamental laws and theories. A major goal of physics is to find the "common ground" that would unite all of these theories into one integrated ], of which all the other known laws would be special cases, and from which the behavior of all matter and energy could be derived (at least in principle).<ref>"Details can be worked out if the situation is simple enough for us to make an approximation, which is almost never, but often we can understand more or less what is happening." from '']'', Vol 1. pp. 2–7</ref> | |||
| ==Particle content== | == Particle content == | ||
| The Standard Model |
The Standard Model includes members of several classes of elementary particles, which in turn can be distinguished by other characteristics, such as ]. | ||
| {{cite book | |||
| |author=S. Braibant, G. Giacomelli, M. Spurio | |||
| |year=2009 | |||
| |title=Particles and Fundamental Interactions: An Introduction to Particle Physics | |||
| |url=http://books.google.com/?id=0Pp-f0G9_9sC&pg=PA314&lpg=PA314&dq=61+fundamental+particles#v=onepage&q=61%20fundamental%20particles&f=false | |||
| |pages=313–314 | |||
| |publisher=] | |||
| |isbn=978-94-007-2463-1 | |||
| }}</ref> | |||
| All particles can be summarized as follows: | |||
| ]s are ]s and ]s; and ]s are hadrons and ]s).]] | |||
| {{Elementary particles|SM=yes}} | |||
| === Fermions === | |||
| {| class="wikitable" style="text-align:left;" | |||
| <!-- | |||
| |+ Elementary Particles | |||
| ], T<sub>3</sub>, ], Y<sub>W</sub>, and ] of all known elementary particles, rotated by the ] to show electric charge, Q, roughly along the vertical. The neutral ] (gray square) breaks the ] and interacts with other particles to give them mass.]] | |||
| |- | |||
| --> | |||
| | | |||
| ! scope="col" | ] | |||
| ! scope="col" | ] | |||
| ! scope="col" | ] | |||
| ! scope="col" | ] | |||
| ! scope="col" | Total | |||
| |- | |||
| ! scope="row" | ]s | |||
| |2 | |||
| |3 | |||
| |Pair | |||
| |3 | |||
| |36 | |||
| |- | |||
| ! scope="row" | ]s | |||
| |2 | |||
| |3 | |||
| |Pair | |||
| |None | |||
| |12 | |||
| |- | |||
| ! scope="row" | ]s | |||
| |1 | |||
| |1 | |||
| |Own | |||
| |] | |||
| |8 | |||
| |- | |||
| ! scope="row" | ] | |||
| |1 | |||
| |1 | |||
| |Pair | |||
| |None | |||
| |2 | |||
| |- | |||
| ! scope="row" | ] | |||
| |1 | |||
| |1 | |||
| |Own | |||
| |None | |||
| |1 | |||
| |- | |||
| ! scope="row" | ] | |||
| |1 | |||
| |1 | |||
| |Own | |||
| |None | |||
| |1 | |||
| |- | |||
| ! scope="row" | ] | |||
| |1 | |||
| |1 | |||
| |Own | |||
| |None | |||
| |1 | |||
| |- | |||
| !colspan="5" !scope="row"| Total | |||
| |'''61''' | |||
| |} | |||
| The Standard Model includes 12 ]s of ] {{1/2}}, known as ]s.<ref name=":0">{{Cite web |title=The Standard Model |url=https://www-project.slac.stanford.edu/e158/StandardModel.html |url-status=live |archive-url=https://web.archive.org/web/20060620190613/http://www-project.slac.stanford.edu/e158/StandardModel.html |archive-date=June 20, 2006 |access-date=January 18, 2024 |website=]}}</ref> Fermions respect the ], meaning that two ] cannot simultaneously occupy the same quantum state in the same atom.<ref>{{Cite journal |last=Eisert |first=Jens |date=January 22, 2013 |title=Pauli Principle, Reloaded |url=https://physics.aps.org/articles/v6/8 |journal=Physics |language=en |volume=6 |issue=4 |pages=8 |doi=10.1103/PhysRevLett.110.040404|pmid=25166142 |arxiv=1210.5531 }}</ref> Each fermion has a corresponding ], which are particles that have corresponding properties with the exception of ] ].<ref>{{Cite web |date=January 24, 2002 |title=What is antimatter? |url=https://www.scientificamerican.com/article/what-is-antimatter-2002-01-24/ |url-status=live |archive-url=https://web.archive.org/web/20140331153524/http://www.scientificamerican.com/article/what-is-antimatter-2002-01-24 |archive-date=March 31, 2014 |access-date=January 19, 2024 |website=]}}</ref> Fermions are classified based on how they interact, which is determined by the charges they carry, into two groups: ] and ]. Within each group, pairs of particles that exhibit similar physical behaviors are then grouped into ] (see the table). Each member of a generation has a greater mass than the corresponding particle of generations prior. Thus, there are three generations of quarks and leptons.<ref name=":1">{{cite web |title=Standard Model - ATLAS Physics Cheat Sheet |url=https://cds.cern.ch/record/2759492/files/Standard%20Model%20-%20ATLAS%20Physics%20Cheat%20Sheet.pdf |access-date=2024-01-19 |website=] |publisher=]}}</ref> As first-generation particles do not decay, they comprise all of ordinary (]ic) matter. Specifically, all atoms consist of electrons orbiting around the ], ultimately constituted of up and down quarks. On the other hand, second- and third-generation charged particles decay with very short ] and can only be observed in high-energy environments. Neutrinos of all generations also do not decay, and pervade the universe, but rarely interact with baryonic matter. | |||
| ===Fermions=== | |||
| There are six quarks: ], ], ], ], ], and ].<ref name=":0" /><ref name=":1" /> Quarks carry ], and hence interact via the ]. The ] phenomenon results in quarks being strongly bound together such that they form color-neutral composite particles called ]s; quarks cannot individually exist and must always bind with other quarks. Hadrons can contain either a quark-antiquark pair (]s) or three quarks (]s).<ref>{{cite web |title=Color Charge and Confinement |url=https://fafnir.phyast.pitt.edu/particles/color.html |url-status=live |archive-url=https://web.archive.org/web/20020322100232/http://fafnir.phyast.pitt.edu/particles/color.html |archive-date=March 22, 2002 |access-date=January 8, 2024 |website=]}}</ref> The lightest baryons are the ]: the ] and ]. Quarks also carry ] and ], and thus interact with other fermions through ] and ]. The six leptons consist of the ], ], ], ], ], and ]. The leptons do not carry color charge, and do not respond to strong interaction. The charged leptons carry an ] of −1 '']'', while the three ]s carry zero electric charge. Thus, the neutrinos' motions are influenced by only the ] and ], making them difficult to observe. | |||
| ], T<sub>3</sub>, ], Y<sub>W</sub>, and ] of all known elementary particles, rotated by the ] to show electric charge, Q, roughly along the vertical. The neutral ] (gray square) breaks the ] and interacts with other particles to give them mass.]] | |||
| === Gauge bosons === | |||
| The Standard Model includes 12 ]s of ] known as ]s. According to the ], fermions respect the ]. Each fermion has a corresponding ]. | |||
| [[File:Standard Model – All Feynman diagram vertices.svg|upright=1.5|thumb|right|class=skin-invert-image|Interactions in the Standard Model. All Feynman diagrams in the model are built from combinations of these vertices. ''q'' is any quark, ''g'' is a gluon, | |||
| ''X'' is any charged particle, γ is a photon, ''f'' is any fermion, ''m'' is any particle with mass (with the possible exception of the neutrinos), ''m''<sub>B</sub> is any boson with mass. | |||
| The fermions of the Standard Model are classified according to how they interact (or equivalently, by what ] they carry). There are six ]s (], ], ], ], ], ]), and six ]s (], ], ], ], ], ]). Pairs from each classification are grouped together to form a ], with corresponding particles exhibiting similar physical behavior (see table). | |||
| In diagrams with multiple particle labels separated by '/', one particle label is chosen. In diagrams with particle labels separated by '<nowiki>|</nowiki>', the labels must be chosen in the same order. For example, in the four boson electroweak case the valid diagrams are WWWW, WWZZ, WWγγ, WWZγ. The conjugate of each listed vertex (reversing the direction of arrows) is also allowed.<ref>{{cite thesis |type=PhD |last=Lindon |first=Jack |date=2020 |title=Particle Collider Probes of Dark Energy, Dark Matter and Generic Beyond Standard Model Signatures in Events With an Energetic Jet and Large Missing Transverse Momentum Using the ATLAS Detector at the LHC |publisher=CERN |url=https://cds.cern.ch/record/2746537/ }}</ref>]] | |||
| The defining property of the quarks is that they carry ], and hence, interact via the ]. A phenomenon called ] results in quarks being perpetually (or at least since very soon after the start of the ]) bound to one another, forming color-neutral composite particles (]s) containing either a quark and an antiquark (]s) or three quarks (]s). The familiar ] and the ] are the two baryons having the smallest mass. Quarks also carry ] and ]. Hence they interact with other fermions both ] and via the ]. | |||
| The Standard Model includes 4 kinds of ]s of ] 1,<ref name=":0" /> with bosons being quantum particles containing an integer spin. The gauge bosons are defined as ]s, as they are responsible for mediating the ]s. The Standard Model explains the four fundamental forces as arising from the interactions, with fermions ] ] force carrier particles, thus mediating the forces. At a macroscopic scale, this manifests as a ].<ref>{{cite journal |last1=Jaeger |first1=Gregg |year=2021 |title=Exchange Forces in Particle Physics |journal=Foundations of Physics |volume=51 |issue=1 |page=13 |bibcode=2021FoPh...51...13J |doi=10.1007/s10701-021-00425-0 |s2cid=231811425}}</ref> As a result, they do not follow the Pauli exclusion principle that constrains fermions; bosons do not have a theoretical limit on their ]. The types of gauge bosons are described below. | |||
| The remaining six fermions do not carry colour charge and are called leptons. The three ]s do not carry electric charge either, so their motion is directly influenced only by the ], which makes them notoriously difficult to detect. However, by virtue of carrying an electric charge, the electron, muon, and tau all interact electromagnetically. | |||
| * ]: ]s mediate the electromagnetic force, responsible for interactions between electrically charged particles. The photon is massless and is described by the theory of ] (QED). | |||
| * ]: ]s mediate the strong interactions, which binds quarks to each other by influencing the ], with the interactions being described in the theory of ] (QCD). They have no mass, and there are eight distinct gluons, with each being denoted through a color-anticolor charge combination (e.g. red–antigreen).{{NoteTag|Although nine color–anticolor combinations mathematically exist, gluons form color octet particles. As one color-symmetric combination is linear and forms a color singlet particles, there are eight possible gluons.<ref>{{Cite book |last1=Cahn |first1=Robert N. |title=The Experimental Foundations of Particle Physics |last2=Goldbaher |first2=Gerson |publisher=] |year=2010 |isbn=978-0521521475 |edition=2nd |publication-date=August 31, 2009 |pages=306 |chapter=Quarks, gluons, and jets |chapter-url=http://hitoshi.berkeley.edu/129A/Cahn-Goldhaber/chapter10.pdf |chapter-format=] |archive-url=https://web.archive.org/web/20120714015451/http://hitoshi.berkeley.edu/129A/Cahn-Goldhaber/chapter10.pdf |archive-date=July 14, 2012 |url-status=live}}</ref>}} As gluons have an effective color charge, they can also interact amongst themselves. | |||
| * ]: The ] gauge bosons mediate the weak interactions between all fermions, being responsible for ]. They contain mass, with the {{SubatomicParticle|Z boson}} having more mass than the {{SubatomicParticle|W boson+-}}. The weak interactions involving the {{SubatomicParticle|W boson+-}} act only on ]. The {{SubatomicParticle|W boson+-}} carries an electric charge of +1 and −1 and couples to the electromagnetic interaction. The electrically neutral {{SubatomicParticle|Z boson}} boson interacts with both left-handed particles and right-handed antiparticles. These three gauge bosons along with the photons are grouped together, as collectively mediating the ] interaction. | |||
| * ]: It is currently unexplained in the Standard Model, as the hypothetical mediating particle ] has been proposed, but not observed.<ref>{{Cite web |last=Hooper |first=Dan |date=2022-05-19 |title=What is the Standard Model of particle physics, and why are scientists looking beyond it? |url=https://www.astronomy.com/science/what-is-the-standard-model-of-particle-physics-and-why-are-scientists-looking-beyond-it/ |access-date=2024-01-20 |website=] |language=en-US}}</ref> This is due to the incompatibility of quantum mechanics and ], regarded as being the best explanation for gravity. In general relativity, gravity is explained as being the geometric curving of spacetime.<ref>{{Cite news |last=Butterworth |first=Jon |date=2014-06-01 |title=Gravity versus the Standard Model |url=https://www.theguardian.com/science/life-and-physics/2014/jun/01/gravity-versus-the-standard-model |access-date=2024-01-20 |work=] |language=en-GB |issn=0261-3077}}</ref> | |||
| The ] calculations, which are a graphical representation of the ] approximation, invoke "force mediating particles", and when applied to analyze ] are in reasonable agreement with the data. However, perturbation theory (and with it the concept of a "force-mediating particle") fails in other situations. These include low-energy quantum chromodynamics, ]s, and ]s. The interactions between all the particles described by the Standard Model are summarized by the diagrams on the right of this section. | |||
| === Higgs boson === | |||
| Each member of a generation has greater mass than the corresponding particles of lower generations. The first generation charged particles do not decay; hence all ordinary (baryonic) matter is made of such particles. Specifically, all atoms consist of electrons orbiting ] ultimately constituted of up and down quarks. Second and third generations charged particles, on the other hand, decay with very short half lives, and are observed only in very high-energy environments. Neutrinos of all generations also do not decay, and pervade the universe, but rarely interact with baryonic matter. | |||
| {{Main|Higgs boson}} | |||
| The Higgs particle is a massive ] elementary particle theorized by ] (]) in 1964, when he showed that Goldstone's 1962 theorem (generic continuous symmetry, which is spontaneously broken) provides a third polarisation of a massive vector field. Hence, Goldstone's original scalar doublet, the massive spin-zero particle, was ], and is a key building block in the Standard Model.<ref> | |||
| ===Gauge bosons=== | |||
| {{cite journal | |||
| ] | |||
| |author=G.S. Guralnik | |||
| |year=2009 | |||
| |title=The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles | |||
| |journal=] | |||
| |volume=24 |issue=14 |pages=2601–2627 | |||
| |arxiv=0907.3466 | |||
| |bibcode=2009IJMPA..24.2601G | |||
| |doi=10.1142/S0217751X09045431 | |||
| |s2cid=16298371 | |||
| }}</ref> It has no intrinsic ], and for that reason is classified as a ] with spin-0.<ref name=":0" /> | |||
| The Higgs boson plays a unique role in the Standard Model, by explaining why the other elementary particles, except the ] and ], are massive. In particular, the Higgs boson explains why the photon has no mass, while the ] are very heavy. Elementary-particle masses and the differences between ] (mediated by the photon) and the ] (mediated by the W and Z bosons) are critical to many aspects of the structure of microscopic (and hence macroscopic) matter. In ], the Higgs boson generates the masses of the leptons (electron, muon, and tau) and quarks. As the Higgs boson is massive, it must interact with itself. | |||
| ] | |||
| Because the Higgs boson is a very massive particle and also decays almost immediately when created, only a very high-energy ] can observe and record it. Experiments to confirm and determine the nature of the Higgs boson using the ] (LHC) at ] began in early 2010 and were performed at ]'s ] until its closure in late 2011. Mathematical consistency of the Standard Model requires that any mechanism capable of generating the masses of elementary particles must become visible{{clarify|reason=Isn't "apparent" or "manifest" needed here instead of "visible"?|date=July 2013}} at energies above {{val|1.4|ul=TeV}};<ref> | |||
| In the Standard Model, ]s are defined as ]s that mediate the strong, weak, and electromagnetic ]s. | |||
| Interactions in physics are the ways that particles influence other particles. At a ], electromagnetism allows particles to interact with one another via ] and ] fields, and gravitation allows particles with mass to attract one another in accordance with Einstein's theory of ]. The Standard Model explains such forces as resulting from matter particles ], known as ''force mediating particles'' (strictly speaking, this is only so if interpreting literally what is actually an ''approximation method'' known as ]){{Citation needed|date=August 2010}}. When a force-mediating particle is exchanged, at a macroscopic level the effect is equivalent to a force influencing both of them, and the particle is therefore said to have ''mediated'' (i.e., been the agent of) that force. The ] calculations, which are a graphical representation of the perturbation theory approximation, invoke "force mediating particles", and when applied to analyze ] are in reasonable agreement with the data. However, perturbation theory (and with it the concept of a "force-mediating particle") fails in other situations. These include low-energy ], ]s, and ]s. | |||
| The gauge bosons of the Standard Model all have ] (as do matter particles). The value of the spin is 1, making them ]s. As a result, they do not follow the ] that constrains ]s: thus bosons (e.g. photons) do not have a theoretical limit on their spatial density (number per volume). The different types of gauge bosons are described below. | |||
| *]s mediate the electromagnetic force between electrically charged particles. The photon is massless and is well-described by the theory of ]. | |||
| *The ] gauge bosons mediate the ]s between particles of different flavors (all ]s and leptons). They are massive, with the {{SubatomicParticle|Z boson}} being more massive than the {{SubatomicParticle|W boson+-}}. The weak interactions involving the {{SubatomicParticle|W boson+-}} exclusively act on ''left-handed'' particles and ''right-handed'' antiparticles only. Furthermore, the {{SubatomicParticle|W boson+-}} carries an electric charge of +1 and −1 and couples to the electromagnetic interaction. The electrically neutral {{SubatomicParticle|Z boson}} boson interacts with both left-handed particles and antiparticles. These three gauge bosons along with the photons are grouped together, as collectively mediating the ] interaction. | |||
| *The eight ]s mediate the ]s between ]d particles (the quarks). Gluons are massless. The eightfold multiplicity of gluons is labeled by a combination of color and anticolor charge (e.g. red–antigreen).<ref group="nb">Technically, there are nine such color–anticolor combinations. However, there is one color-symmetric combination that can be constructed out of a linear superposition of the nine combinations, reducing the count to eight.</ref> Because the gluons have an effective color charge, they can also interact among themselves. The gluons and their interactions are described by the theory of quantum chromodynamics. | |||
| The interactions between all the particles described by the Standard Model are summarized by the diagrams on the right of this section. | |||
| ===Higgs boson=== | |||
| {{Main|Higgs boson}} | |||
| The Higgs particle is a massive ] elementary particle theorized by ], ], ], ], ], and ] in 1964 (see ]) and is a key building block in the Standard Model.<ref> | |||
| {{cite journal | {{cite journal | ||
| |author1=B.W. Lee |author2=C. Quigg |author3=H.B. Thacker |year=1977 | |||
| | author=F. Englert, R. Brout | |||
| | title=Broken Symmetry and the Mass of Gauge Vector Mesons | |||
| | journal=] | |||
| | volume=13 | year=1964 | pages=321–323 | |||
| | doi=10.1103/PhysRevLett.13.321 | |||
| | bibcode=1964PhRvL..13..321E | |||
| | issue=9 | |||
| }}</ref><ref name="Peter W. Higgs 1964 508-509"> | |||
| {{cite journal | |||
| | author=P.W. Higgs | |||
| | title=Broken Symmetries and the Masses of Gauge Bosons | |||
| | journal=] | |||
| | volume=13 | year=1964 | pages=508–509 | |||
| | doi=10.1103/PhysRevLett.13.508 | |||
| | bibcode=1964PhRvL..13..508H | |||
| | issue=16 | |||
| }}</ref><ref> | |||
| {{cite journal | |||
| | author=G.S. Guralnik, C.R. Hagen, T.W.B. Kibble | |||
| | title=Global Conservation Laws and Massless Particles | |||
| | journal=] | |||
| | volume=13 | year=1964 | |||
| | pages=585–587 | |||
| | doi=10.1103/PhysRevLett.13.585 | |||
| | bibcode=1964PhRvL..13..585G | |||
| | issue=20 | |||
| }}</ref><ref> | |||
| {{cite journal | |||
| | author=G.S. Guralnik | |||
| | year=2009 | |||
| | title=The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles | |||
| | journal=] | |||
| | volume=24 | pages=2601–2627 | |||
| | doi=10.1142/S0217751X09045431 | |||
| | arxiv = 0907.3466 | |||
| |bibcode = 2009IJMPA..24.2601G | |||
| | issue=14 }}</ref> It has no intrinsic ], and for that reason is classified as a ] (like the gauge bosons, which have ] spin). | |||
| The Higgs boson plays a unique role in the Standard Model, by explaining why the other elementary particles, except the ] and ], are massive. In particular, the Higgs boson would explain why the photon has no mass, while the ] are very heavy. Elementary particle masses, and the differences between ] (mediated by the photon) and the ] (mediated by the W and Z bosons), are critical to many aspects of the structure of microscopic (and hence macroscopic) matter. In ], the Higgs boson generates the masses of the leptons (electron, muon, and tau) and quarks. As the Higgs boson is massive, it must interact with itself. | |||
| Because the Higgs boson is a very massive particle and also decays almost immediately when created, only a very high energy ] can observe and record it. Experiments to confirm and determine the nature of the Higgs boson using the ] (LHC) at ] began in early 2010, and were performed at ]'s ] until its closure in late 2011. Mathematical consistency of the Standard Model requires that any mechanism capable of generating the masses of elementary particles become visible at energies above {{val|1.4|ul=TeV}};<ref>{{cite journal | |||
| |last=Lee |first=Benjamin W. | |||
| |last2=Quigg |first2=C. | |||
| |last3=Thacker |first3=H. B. | |||
| |year=1977 | |||
| |title=Weak interactions at very high energies: The role of the Higgs-boson mass | |title=Weak interactions at very high energies: The role of the Higgs-boson mass | ||
| |journal=] | |journal=] | ||
| |volume=16 |issue=5 |pages=1519–1531 | |volume=16 |issue=5 |pages=1519–1531 | ||
| |bibcode=1977PhRvD..16.1519L | |||
| |doi=10.1103/PhysRevD.16.1519 | |doi=10.1103/PhysRevD.16.1519 | ||
| }}</ref> therefore, the LHC (designed to collide two {{val|7|u=TeV}} proton beams) was built to answer the question of whether the Higgs boson actually exists.<ref> | |||
| {{cite news | {{cite news | ||
| |url=http://www.cnn.com/2009/TECH/11/11/lhc.large.hadron.collider.beam/index.html | |||
| |work=CNN | |||
| |title=Huge $10 billion collider resumes hunt for 'God particle' - CNN.com | |||
| |accessdate=4 May 2010 | |||
| |date=11 November 2009 | |date=11 November 2009 | ||
| |title=Huge $10 billion collider resumes hunt for 'God particle' | |||
| |url=http://www.cnn.com/2009/TECH/11/11/lhc.large.hadron.collider.beam/index.html | |||
| |publisher=CNN | |||
| |access-date=2010-05-04 | |||
| }}</ref> | }}</ref> | ||
| On 4 July 2012, two of the experiments at the LHC (] and ]) both reported independently that they had found a new particle with a mass of about {{val|125|ul=GeV/c2}} (about 133 proton masses, on the order of {{val|e=-25|u=kg}}), which is "consistent with the Higgs boson".<ref> | |||
| On 4 July 2012, the two main experiments at the LHC (] and ]) both reported independently that they found a new particle with a mass of about {{val|125|ul=GeV/c2}} (about 133 proton masses, on the order of 10<sup>−25</sup> kg), which is "consistent with the Higgs boson." Although it has several properties similar to the predicted "simplest" Higgs,<ref>http://profmattstrassler.com/articles-and-posts/the-higgs-particle/the-discovery-of-the-higgs/higgs-discovery-is-it-a-higgs</ref> they acknowledged that further work would be needed to conclude that it is indeed the Higgs boson, and exactly which version of the Standard Model Higgs is best supported if confirmed.<ref name=cern1207>{{cite news|url=http://press.web.cern.ch/press/PressReleases/Releases2012/PR17.12E.html |title=CERN experiments observe particle consistent with long-sought Higgs boson |publisher=CERN |date=4 July 2012 |accessdate=4 July 2012}}</ref><ref>{{cite web|url=http://cms.web.cern.ch/news/observation-new-particle-mass-125-gev |title=Observation of a New Particle with a Mass of 125 GeV |publisher=Cms.web.cern.ch |date= |accessdate=2012-07-05}}</ref><ref>{{cite web|url=http://www.atlas.ch/news/2012/latest-results-from-higgs-search.html |title=ATLAS Experiment |publisher=Atlas.ch |date=2006-01-01 |accessdate=2012-07-05}}</ref><ref> - ] Announcement (4 July 2012) Of Higgs Boson Discovery.</ref><ref name="NYT-20120704">{{cite news |last=Overbye |first=Dennis |title=A New Particle Could Be Physics’ Holy Grail |url=http://www.nytimes.com/2012/07/05/science/cern-physicists-may-have-discovered-higgs-boson-particle.html |date=July 4, 2012 |newspaper=] |accessdate=July 4, 2012 }}</ref> | |||
| {{cite web | |||
| |date=4 July 2012 | |||
| |title=Observation of a New Particle with a Mass of 125 GeV | |||
| |url=http://cms.web.cern.ch/news/observation-new-particle-mass-125-gev | |||
| |publisher=CERN | |||
| |access-date=2012-07-05 | |||
| }}</ref><ref name="NYT-20120704"> | |||
| {{cite news | |||
| |author=D. Overbye | |||
| |date=4 July 2012 | |||
| |title=A New Particle Could Be Physics' Holy Grail | |||
| |url=https://www.nytimes.com/2012/07/05/science/cern-physicists-may-have-discovered-higgs-boson-particle.html | |||
| |newspaper=The New York Times | |||
| |access-date=2012-07-04 | |||
| }}</ref> On 13 March 2013, it was confirmed to be the searched-for Higgs boson.<ref name="CERN_20130314"> | |||
| {{cite web | |||
| |url=https://home.cern/news/press-release/cern/new-results-indicate-particle-discovered-cern-higgs-boson | |||
| |title=New results indicate that particle discovered at CERN is a Higgs boson | |||
| |date=14 March 2013 | |||
| |publisher=CERN | |||
| |access-date=2020-06-14 | |||
| }}</ref><ref name="CERN_EPS2017"> | |||
| {{cite web | |||
| |url=https://press.cern/update/2017/07/lhc-experiments-delve-deeper-precision | |||
| |title=LHC experiments delve deeper into precision | |||
| |date=11 July 2017 | |||
| |publisher=CERN | |||
| |access-date=2017-07-23 | |||
| |archive-date=14 July 2017 | |||
| |archive-url=https://web.archive.org/web/20170714090456/http://press.cern/update/2017/07/lhc-experiments-delve-deeper-precision | |||
| |url-status=dead | |||
| }}</ref> | |||
| == Theoretical aspects == | |||
| On March 14th, 2013 the Higgs Boson was tentatively confirmed to exist. <ref>http://home.web.cern.ch/about/updates/2013/03/new-results-indicate-new-particle-higgs-boson</ref> | |||
| {{Main|Mathematical formulation of the Standard Model}} | |||
| === Construction of the Standard Model Lagrangian === | |||
| ==Theoretical aspects== | |||
| {{main|Standard Model (mathematical formulation)}} | |||
| ===Construction of the Standard Model Lagrangian=== | |||
| {| class="wikitable collapsible collapsed" | {| class="wikitable collapsible collapsed" | ||
| !colspan=" |
!colspan="6"|Parameters of the Standard Model | ||
| |- | |- | ||
| ! # | |||
| ! Symbol | ! Symbol | ||
| ! Description | ! Description | ||
| Line 349: | Line 263: | ||
| ! Value | ! Value | ||
| |- | |- | ||
| |1 | |||
| |''m''<sub>e</sub> | |''m''<sub>e</sub> | ||
| |Electron mass | |Electron mass | ||
| | | | | ||
| |511 |
|0.511 MeV | ||
| |- | |- | ||
| |2 | |||
| |''m''<sub>μ</sub> | |''m''<sub>μ</sub> | ||
| |Muon mass | |Muon mass | ||
| Line 359: | Line 275: | ||
| |105.7 MeV | |105.7 MeV | ||
| |- | |- | ||
| |3 | |||
| |''m''<sub>τ</sub> | |''m''<sub>τ</sub> | ||
| |Tau mass | |Tau mass | ||
| Line 364: | Line 281: | ||
| |1.78 GeV | |1.78 GeV | ||
| |- | |- | ||
| |4 | |||
| |''m''<sub>u</sub> | |''m''<sub>u</sub> | ||
| |Up quark mass | |Up quark mass | ||
| |''μ''<sub> |
|''μ''<sub>{{overline|MS}}</sub> = 2 GeV | ||
| |1.9 MeV | |1.9 MeV | ||
| |- | |- | ||
| |5 | |||
| |''m''<sub>d</sub> | |''m''<sub>d</sub> | ||
| |Down quark mass | |Down quark mass | ||
| Line 374: | Line 293: | ||
| |4.4 MeV | |4.4 MeV | ||
| |- | |- | ||
| |6 | |||
| |''m''<sub>s</sub> | |''m''<sub>s</sub> | ||
| |Strange quark mass | |Strange quark mass | ||
| Line 379: | Line 299: | ||
| |87 MeV | |87 MeV | ||
| |- | |- | ||
| |7 | |||
| |''m''<sub>c</sub> | |''m''<sub>c</sub> | ||
| |Charm quark mass | |Charm quark mass | ||
| Line 384: | Line 305: | ||
| |1.32 GeV | |1.32 GeV | ||
| |- | |- | ||
| |8 | |||
| |''m''<sub>b</sub> | |''m''<sub>b</sub> | ||
| |Bottom quark mass | |Bottom quark mass | ||
| Line 389: | Line 311: | ||
| |4.24 GeV | |4.24 GeV | ||
| |- | |- | ||
| |9 | |||
| |''m''<sub>t</sub> | |''m''<sub>t</sub> | ||
| |Top quark mass | |Top quark mass | ||
| | |
| On shell scheme | ||
| | |
|173.5 GeV | ||
| |- | |- | ||
| |10 | |||
| |''θ''<sub>12</sub> | |''θ''<sub>12</sub> | ||
| |CKM 12-mixing angle | |CKM 12-mixing angle | ||
| Line 399: | Line 323: | ||
| |13.1° | |13.1° | ||
| |- | |- | ||
| |11 | |||
| |''θ''<sub>23</sub> | |''θ''<sub>23</sub> | ||
| |CKM 23-mixing angle | |CKM 23-mixing angle | ||
| Line 404: | Line 329: | ||
| |2.4° | |2.4° | ||
| |- | |- | ||
| |12 | |||
| |''θ''<sub>13</sub> | |''θ''<sub>13</sub> | ||
| |CKM 13-mixing angle | |CKM 13-mixing angle | ||
| Line 409: | Line 335: | ||
| |0.2° | |0.2° | ||
| |- | |- | ||
| |13 | |||
| |''δ'' | |''δ'' | ||
| |CKM |
|CKM CP violation Phase | ||
| | | | | ||
| |0.995 | |0.995 | ||
| |- | |- | ||
| |14 | |||
| |''g''<sub>1</sub> or ''g''' | |||
| |''g''<sub>1</sub> or ''g''{{'}} | |||
| |U(1) gauge coupling | |U(1) gauge coupling | ||
| |''μ''<sub>{{overline|MS}}</sub> = ''m''<sub>Z</sub> | |''μ''<sub>{{overline|MS}}</sub> = ''m''<sub>Z</sub> | ||
| |0.357 | |0.357 | ||
| |- | |- | ||
| |15 | |||
| |''g''<sub>2</sub> or ''g'' | |''g''<sub>2</sub> or ''g'' | ||
| |SU(2) gauge coupling | |SU(2) gauge coupling | ||
| Line 424: | Line 353: | ||
| |0.652 | |0.652 | ||
| |- | |- | ||
| |16 | |||
| |''g''<sub>3</sub> or ''g''<sub>s</sub> | |''g''<sub>3</sub> or ''g''<sub>s</sub> | ||
| |SU(3) gauge coupling | |SU(3) gauge coupling | ||
| Line 429: | Line 359: | ||
| |1.221 | |1.221 | ||
| |- | |- | ||
| |17 | |||
| |''θ''<sub>QCD</sub> | |''θ''<sub>QCD</sub> | ||
| |QCD |
|QCD vacuum angle | ||
| | | | | ||
| |~0 | |~0 | ||
| |- | |- | ||
| |18 | |||
| |''v'' | |''v'' | ||
| |Higgs vacuum expectation value | |Higgs vacuum expectation value | ||
| Line 439: | Line 371: | ||
| |246 GeV | |246 GeV | ||
| |- | |- | ||
| |19 | |||
| |''m''<sub>H</sub> | |''m''<sub>H</sub> | ||
| |Higgs mass | |Higgs mass | ||
| | | | | ||
| |{{val|125.09|0.24|u=GeV}} | |||
| |~ 125 GeV (tentative) | |||
| |} | |} | ||
| Technically, ] provides the mathematical framework for the Standard Model, in which a ] controls the dynamics and kinematics of the theory. Each kind of particle is described in terms of a dynamical ] that pervades ]. The construction of the Standard Model proceeds following the modern method of constructing most field theories: by first postulating a set of symmetries of the system, and then by writing down the most general ] Lagrangian from its particle (field) content that observes these symmetries. | |||
| Technically, ] provides the mathematical framework for the Standard Model, in which a ] controls the dynamics and kinematics of the theory. Each kind of particle is described in terms of a dynamical ] that pervades ].<ref>{{cite journal | author=Gregg Jaeger | year=2021 | title=The Elementary Particles of Quantum Fields | journal=] | volume=23 | issue=11 | pages=1416 | doi=10.3390/e23111416 | pmid=34828114 | pmc=8623095 | bibcode=2021Entrp..23.1416J | doi-access=free }}</ref> | |||
| The ] ] is postulated for all relativistic quantum field theories. It consists of the familiar ], ] and the inertial reference frame invariance central to the theory of ]. The ] SU(3)×SU(2)×U(1) gauge symmetry is an ] that essentially defines the Standard Model. Roughly, the three factors of the gauge symmetry give rise to the three fundamental interactions. The fields fall into different ] of the various symmetry groups of the Standard Model (see table). Upon writing the most general Lagrangian, one finds that the dynamics depend on 19 parameters, whose numerical values are established by experiment. The parameters are summarized in the table above (note: with the Higgs mass is at 125 GeV, the Higgs self-coupling strength ''λ'' ~ 1/8). | |||
| The construction of the Standard Model proceeds following the modern method of constructing most field theories: by first postulating a set of symmetries of the system, and then by writing down the most general ] Lagrangian from its particle (field) content that observes these symmetries. | |||
| The ] ] is postulated for all relativistic quantum field theories. It consists of the familiar ], ] and the inertial reference frame invariance central to the theory of ]. The ] SU(3) × SU(2) × U(1) ] is an ] that essentially defines the Standard Model. Roughly, the three factors of the gauge symmetry give rise to the three fundamental interactions. The fields fall into different ] of the various symmetry groups of the Standard Model (see table). Upon writing the most general Lagrangian, one finds that the dynamics depends on 19 parameters, whose numerical values are established by experiment. The parameters are summarized in the table (made visible by clicking "show") above. | |||
| ====Quantum chromodynamics sector==== | |||
| ==== Quantum chromodynamics sector ==== | |||
| {{Main|Quantum chromodynamics}} | {{Main|Quantum chromodynamics}} | ||
| The quantum chromodynamics (QCD) sector defines the interactions between quarks and gluons, with SU(3) symmetry, generated by |
The quantum chromodynamics (QCD) sector defines the interactions between quarks and gluons, which is a ] with SU(3) symmetry, generated by <math>T^a = \lambda^a/2</math>. Since leptons do not interact with gluons, they are not affected by this sector. The Dirac Lagrangian of the quarks coupled to the gluon fields is given by | ||
| <math display="block">\mathcal{L}_\text{QCD} = \overline{\psi} i\gamma^\mu D_{\mu} \psi - \frac{1}{4} G^a_{\mu\nu} G^{\mu\nu}_a,</math> | |||
| where <math>\psi</math> is a three component column vector of ]s, each element of which refers to a quark field with a specific ] (i.e. red, blue, and green) and summation over ] (i.e. up, down, strange, etc.) is implied. | |||
| <math>G_\mu^a</math> is the SU(3) gauge field containing the gluons, <math>\gamma^\mu</math> are the Dirac matrices, D and U are the Dirac spinors associated with up- and down-type ]s, and g<sub>s</sub> is the strong coupling constant. | |||
| The gauge covariant derivative of QCD is defined by <math>D_{\mu} \equiv \partial_\mu - i g_\text{s}\frac{1}{2}\lambda^a G_\mu^a</math>, where | |||
| ====Electroweak sector==== | |||
| * {{math|''γ''{{isup|''μ''}}}} are the ], | |||
| * {{math|''G''{{su|lh=0.9|b=''μ''|p=''a''}}}} is the 8-component (<math>a = 1, 2, \dots, 8</math>) SU(3) gauge field, | |||
| * {{math|''λ''{{su|lh=0.9|p=''a''}}}} are the 3 × 3 ], generators of the SU(3) color group, | |||
| * {{math|''G''{{su|lh=0.9|b=''μν''|p=''a''}}}} represents the ], and | |||
| * {{math|''g''<sub>s</sub>}} is the strong coupling constant. | |||
| The QCD Lagrangian is invariant under local SU(3) gauge transformations; i.e., transformations of the form <math>\psi \rightarrow \psi' = U\psi</math>, where <math>U = e^{-i g_\text{s}\lambda^a \phi^{a}(x)}</math> is 3 × 3 unitary matrix with determinant 1, making it a member of the group SU(3), and <math>\phi^{a}(x)</math> is an arbitrary function of spacetime. | |||
| ==== Electroweak sector ==== | |||
| {{Main|Electroweak interaction}} | {{Main|Electroweak interaction}} | ||
| The electroweak sector is a ] with the |
The electroweak sector is a ] with the symmetry group {{nowrap|U(1) × SU(2)<sub>L</sub>}}, | ||
| <math display="block">\mathcal{L}_\text{EW} = \overline{Q}_{\text{L}j} i\gamma^\mu D_{\mu} Q_{\text{L}j} + \overline{u}_{\text{R}j} i\gamma^\mu D_{\mu} u_{\text{R}j} + \overline{d}_{\text{R}j} i\gamma^\mu D_{\mu} d_{\text{R}j} + \overline{\ell}_{\text{L}j} i\gamma^\mu D_{\mu} \ell_{\text{L}j} + \overline{e}_{\text{R}j} i\gamma^\mu D_{\mu} e_{\text{R}j} - \tfrac{1}{4} W_a^{\mu\nu} W_{\mu\nu}^a - \tfrac{1}{4} B^{\mu\nu} B_{\mu\nu}, </math> | |||
| :<math> | |||
| where the subscript <math>j</math> sums over the three generations of fermions; <math>Q_\text{L}, u_\text{R}</math>, and <math>d_\text{R}</math> are the left-handed doublet, right-handed singlet up type, and right handed singlet down type quark fields; and <math>\ell_\text{L}</math> and <math>e_\text{R}</math> are the left-handed doublet and right-handed singlet lepton fields. | |||
| \mathcal{L}_\mathrm{EW} = | |||
| \sum_\psi\bar\psi\gamma^\mu | |||
| \ |
The electroweak ] is defined as <math>D_\mu \equiv \partial_\mu - ig' \tfrac12 Y_\text{W} B_\mu - ig \tfrac{1}{2} \vec\tau_\text{L} \vec W_\mu</math>, where | ||
| * {{mvar|B<sub>μ</sub>}} is the U(1) gauge field, | |||
| * {{math|''Y''<sub>W</sub>}} is the ] – the generator of the U(1) group, | |||
| * {{math|{{vec|''W''}}<sub>''μ''</sub>}} is the 3-component SU(2) gauge field, | |||
| * {{math|{{overset|lh=0.5|→|''τ''}}<sub>L</sub>}} are the ] – infinitesimal generators of the SU(2) group – with subscript L to indicate that they only act on ''left''-chiral fermions, | |||
| * {{mvar|g'}} and {{mvar|g}} are the U(1) and SU(2) coupling constants respectively, | |||
| * <math>W^{a\mu\nu}</math> (<math>a = 1, 2, 3</math>) and <math>B^{\mu\nu}</math> are the ]s for the weak isospin and weak hypercharge fields. | |||
| Notice that the addition of fermion mass terms into the electroweak Lagrangian is forbidden, since terms of the form <math>m\overline\psi\psi</math> do not respect {{nowrap|U(1) × SU(2)<sub>L</sub>}} gauge invariance. Neither is it possible to add explicit mass terms for the U(1) and SU(2) gauge fields. The Higgs mechanism is responsible for the generation of the gauge boson masses, and the fermion masses result from Yukawa-type interactions with the Higgs field. | |||
| where ''B''<sub>''μ''</sub> is the U(1) gauge field; ''Y''<sub>W</sub> is the ]—the generator of the U(1) group; <math>\vec{W}_\mu</math> is the | |||
| three-component SU(2) gauge field; <math>\vec{\tau}_\mathrm{L}</math> are the ]—infinitesimal generators of the SU(2) group. The subscript L indicates that they only act on left fermions; ''g''′ and ''g'' are coupling constants. | |||
| ====Higgs sector==== | ==== Higgs sector ==== | ||
| {{Main|Higgs mechanism}} | {{Main|Higgs mechanism}} | ||
| In the Standard Model, the ] is |
In the Standard Model, the ] is an SU(2){{sub|L}} doublet of complex ] fields with four degrees of freedom: | ||
| <math display="block"> | |||
| \varphi={ |
\varphi = \begin{pmatrix} \varphi^+ \\ \varphi^0 \end{pmatrix} | ||
| = \frac{1}{\sqrt{2}} \begin{pmatrix} \varphi_1 + i\varphi_2 \\ \varphi_3 + i\varphi_4 \end{pmatrix}, | |||
| \left( | |||
| \begin{array}{c} | |||
| \varphi^+ \\ \varphi^0 | |||
| \end{array} | |||
| \right)\;, | |||
| </math> | </math> | ||
| where the |
where the superscripts + and 0 indicate the electric charge <math>Q</math> of the components. The weak hypercharge <math>Y_\text{W}</math> of both components is 1. Before symmetry breaking, the Higgs Lagrangian is | ||
| <math display="block"> \mathcal{L}_\text{H} = \left(D_{\mu}\varphi\right)^{\dagger} \left(D^{\mu}\varphi \right) - V(\varphi),</math> | |||
| where <math>D_{\mu}</math> is the electroweak gauge covariant derivative defined above and <math>V(\varphi)</math> is the potential of the Higgs field. The square of the covariant derivative leads to three and four point interactions between the electroweak gauge fields <math>W^{a}_{\mu}</math> and <math>B_{\mu}</math> and the scalar field <math>\varphi</math>. The scalar potential is given by | |||
| <math display="block"> V(\varphi) = -\mu^2\varphi^{\dagger}\varphi + \lambda \left( \varphi^{\dagger}\varphi \right)^2, </math> | |||
| where <math>\mu^2>0</math>, so that <math>\varphi</math> acquires a non-zero ], which generates masses for the Electroweak gauge fields (the Higgs mechanism), and <math>\lambda>0</math>, so that the potential is bounded from below. The quartic term describes self-interactions of the scalar field <math>\varphi</math>. | |||
| The minimum of the potential is degenerate with an infinite number of equivalent ] solutions, which occurs when <math>\varphi^{\dagger}\varphi = \tfrac{\mu^2}{2\lambda}</math>. It is possible to perform a ] on <math>\varphi</math> such that the ground state is transformed to a basis where <math>\varphi_1 = \varphi_2 = \varphi_4 = 0</math> and <math>\varphi_3 = \tfrac{\mu}{\sqrt{\lambda}} \equiv v </math>. This breaks the symmetry of the ground state. The expectation value of <math>\varphi</math> now becomes | |||
| Before symmetry breaking, the Higgs Lagrangian is: | |||
| <math display="block"> \langle \varphi \rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 0 \\ v \end{pmatrix},</math> | |||
| :<math>\mathcal{L}_\mathrm{H} = \varphi^\dagger | |||
| where <math>v</math> has units of mass and sets the scale of electroweak physics. This is the only dimensional parameter of the Standard Model and has a measured value of ~{{val|246|u=GeV/c2}}. | |||
| \left({\partial^\mu}- | |||
| {i\over2} \left( g'Y_\mathrm{W}B^\mu + g\vec\tau\vec W^\mu \right)\right) | |||
| \left(\partial_\mu + {i\over2} \left( g'Y_\mathrm{W}B_\mu | |||
| +g\vec\tau\vec W_\mu \right)\right)\varphi \ - \ {\lambda^2\over4}\left(\varphi^\dagger\varphi-v^2\right)^2\;,</math> | |||
| After symmetry breaking, the masses of the W and Z are given by <math>m_\text{W}=\frac{1}{2}gv</math> and <math> m_\text{Z}=\frac{1}{2}\sqrt{g^2+g'^2}v</math>, which can be viewed as predictions of the theory. The photon remains massless. The mass of the ] is <math>m_\text{H}=\sqrt{2\mu^2}=\sqrt{2\lambda}v</math>. Since <math>\mu</math> and <math>\lambda</math> are free parameters, the Higgs's mass could not be predicted beforehand and had to be determined experimentally. | |||
| which can also be written as: | |||
| :<math>\mathcal{L}_\mathrm{H} = \left| | |||
| \left(\partial_\mu + {i\over2} \left( g'Y_\mathrm{W}B_\mu | |||
| +g\vec\tau\vec W_\mu \right)\right)\varphi\right|^2 \ - \ {\lambda^2\over4}\left(\varphi^\dagger\varphi-v^2\right)^2\;.</math> | |||
| ==== Yukawa sector ==== | |||
| ===The relation of colour charge to electric charge for fermions=== | |||
| The ] terms are: | |||
| <math display="block">\mathcal{L}_\text{Yukawa} = (Y_\text{u})_{mn}(\bar{Q}_\text{L})_m \tilde{\varphi}(u_\text{R})_n + (Y_\text{d})_{mn}(\bar{Q}_\text{L})_m \varphi(d_\text{R})_n + (Y_\text{e})_{mn}(\bar{\ell}_\text{L})_m {\varphi}(e_\text{R})_n + \mathrm{h.c.} </math> | |||
| where <math>Y_\text{u}</math>, <math>Y_\text{d}</math>, and <math>Y_\text{e}</math> are {{math|3 × 3}} matrices of Yukawa couplings, with the {{mvar|mn}} term giving the coupling of the generations {{mvar|m}} and {{mvar|n}}, and h.c. means Hermitian conjugate of preceding terms. The fields <math>Q_\text{L}</math> and <math>\ell_\text{L}</math> are left-handed quark and lepton doublets. Likewise, <math>u_\text{R}, d_\text{R}</math> and <math>e_\text{R}</math> are right-handed up-type quark, down-type quark, and lepton singlets. Finally <math>\varphi</math> is the Higgs doublet and <math>\tilde{\varphi} = i\tau_2\varphi^{*}</math> is its charge conjugate state. | |||
| The Yukawa terms are invariant under the SU(2){{sub|L}} × U(1){{sub|Y}} gauge symmetry of the Standard Model and generate masses for all fermions after spontaneous symmetry breaking. | |||
| Dirac has shown how Einstein's expression for the relation of energy to momentum in Special Relativity can be factored into two linear parts using 4x4 Dirac matrices.<ref>Dirac, P.A.M., The Principles of Quantum Mechanics, 4th edition (Oxford University Press) ISBN 0-19-852011-5</ref> | |||
| == Fundamental interactions == | |||
| This can also be done using 2x2 Pauli matrices (labelled K,L,M) because two inertial observers agree on the component of momentum Q orthogonal to the component of momentum P in the direction of a Lorentz boost. | |||
| {{Main|Fundamental interaction}} | |||
| The Standard Model describes three of the four fundamental interactions in nature; only gravity remains unexplained. In the Standard Model, such an interaction is described as an exchange of ]s between the objects affected, such as a ] for the electromagnetic force and a ] for the strong interaction. Those particles are called ]s or messenger ].<ref>{{Cite web|url=https://home.cern/science/physics/standard-model|title=The Standard Model|website=CERN|date=15 December 2023 }}</ref> | |||
| {| style="margin: 1em auto 1em auto;" class="wikitable floatcenter" | |||
| :<math>(E/c)^2 - P^2 - Q^2 - (mc)^2I = (E/c + rKP + gLQ + mcbM)(E/c - rKP - gLQ - mcbM)</math> | |||
| |+ The four fundamental interactions of nature<ref>{{cite web|url=http://www.pha.jhu.edu/~dfehling/particle.gif |title=Standard Model of Particles and Interactions |author=<!--Staff writer(s); no by-line.--> |website=jhu.edu |publisher=] |access-date=18 August 2016 |url-status=dead |archive-url=https://web.archive.org/web/20160304133522/https://www.pha.jhu.edu/~dfehling/particle.gif |archive-date=4 March 2016 }}</ref> | |||
| ! style="" rowspan="2" | Property/Interaction | |||
| ! style="background-color:#8080BF" rowspan="2" |Gravitation | |||
| ! style="background-color:#BFA080" colspan="2" |Electroweak | |||
| ! style="background-color:#80BF80" colspan="2" |Strong | |||
| |- | |||
| ! style="background-color:#BFBF80" |Weak | |||
| ! style="background-color:#BF8080" |Electromagnetic | |||
| ! style="background-color:#AAD4AA" |<small>Fundamental</small> | |||
| ! style="background-color:#D5EAD5" |<small>Residual</small> | |||
| |- | |||
| |Mediating particles | |||
| | align="center" {{Not yet}} observed<br /><small>(] hypothesised)</small> | |||
| | align="center" |] | |||
| | align="center" |] (photon) | |||
| | align="center" |Gluons | |||
| | align="center" |], ] and ] ]s | |||
| |- | |||
| |Affected particles | |||
| | align="center" |All particles | |||
| | align="center" |Left-handed ] | |||
| | align="center" |Electrically charged | |||
| | align="center" |Quarks, ]s | |||
| | align="center" |]s | |||
| |- | |||
| |Acts on | |||
| | align="center" | ] | |||
| | align="center" |] | |||
| | align="center" |Electric charge | |||
| | align="center" |] | |||
| | align="center" | | |||
| |- | |||
| |Bound states formed | |||
| | align="center" |Planets, stars, galaxies, galaxy groups | |||
| | align="center" {{n/a}} | |||
| | align="center" |Atoms, molecules | |||
| | align="center" |Hadrons | |||
| | align="center" |Atomic nuclei | |||
| |- | |||
| |Strength at the scale of quarks<br /> (relative to electromagnetism) | |||
| | align="center" |{{val||e=-41}} <small>(predicted)</small> | |||
| | align="center" |{{val||e=-4}} | |||
| | align="center" |1 | |||
| | align="center" |60 | |||
| | align="center" {{No|Not applicable <br />to quarks}} | |||
| |- | |||
| |Strength at the scale of <br />protons/neutrons <br /> (relative to electromagnetism) | |||
| | align="center" |{{val||e=-36}} <small>(predicted)</small> | |||
| | align="center" |{{val||e=-7}} | |||
| | align="center" |1 | |||
| | align="center" {{No|Not applicable <br />to hadrons}} | |||
| | align="center" |20 | |||
| |} | |||
| {{Unreferenced section|date=June 2021}} | |||
| This is true for all 3! = 6 permutations of K,L,M where r,g,b equal +1 or -1. | |||
| The set {I,K,L,M} forms the basis of a 4-dimensional vector space. | |||
| === Gravity === | |||
| For leptons r,g,b all equal -1 and for quarks two of r,g,b are equal to +1 and the third equals -1. | |||
| {{See also|Quantum gravity|Gravity}} | |||
| The signs are all negated for anti-particles as in the equation above. | |||
| ] | |||
| The 3 cyclic permutations KLM = MKL = LMK count the number of plus signs (say) for r,g,b which is 0 for leptons and 2 for quarks. | |||
| Despite being perhaps the most familiar fundamental interaction, gravity is not described by the Standard Model, due to contradictions that arise when combining general relativity, the modern theory of gravity, and quantum mechanics<ref>{{Cite journal |last=Ashtekar |first=Abhay |date=2005-09-29 |title=Gravity and the quantum |url=https://iopscience.iop.org/article/10.1088/1367-2630/7/1/198 |journal=New Journal of Physics |volume=7 |pages=198–198 |doi=10.1088/1367-2630/7/1/198 |issn=1367-2630|arxiv=gr-qc/0410054 }}</ref><ref>{{Cite journal |last=Kuchař |first=Karel V. |date=2011-07-31 |title=TIME AND INTERPRETATIONS OF QUANTUM GRAVITY |url=https://www.worldscientific.com/doi/abs/10.1142/S0218271811019347 |journal=International Journal of Modern Physics D |language=en |volume=20 |issue=supp01 |pages=3–86 |doi=10.1142/S0218271811019347 |issn=0218-2718}}</ref>. However, gravity is so weak at microscopic scales, that it is essentially unmeasurable. The ] is postulated to be the mediating particle, but has not yet been proved to exist<ref>{{Cite journal |last=Carney |first=Daniel |date=2024 |title=Graviton detection and the quantization of gravity |url=https://journals.aps.org/prd/abstract/10.1103/PhysRevD.109.044009 |journal=Physical Review D |volume=109 |issue=4 |doi=10.1103/PhysRevD.109.044009|arxiv=2308.12988 }}</ref>. | |||
| The 3 cyclic permutations MLK = LKM = KML count the number of minus signs (say) for r,g,b which is 3 for leptons and 1 for quarks. | |||
| === Electromagnetism === | |||
| For material particles r,g,b all equal -1 which is always true for leptons and true for three distinct quarks with r,g,b equal to -1 separately or a quark and an appropriate anti-quark. | |||
| {{See also|Electromagnetism|Quantum electrodynamics}} | |||
| Electromagnetism is the only long-range force in the Standard Model. It is mediated by photons and couples to electric charge.<ref>{{Cite web |date=2023-12-04 |title=The Standard Model |url=https://home.cern/science/physics/standard-model |access-date=2023-12-17 |website=CERN |language=en}}</ref> Electromagnetism is responsible for a wide range of phenomena including ], ], ]s and ]. Electromagnetic interactions in the Standard Model are described by quantum electrodynamics. | |||
| === Weak nuclear force === | |||
| This mathematical symmetry implies the existence of a complementary anti-Universe composed of anti-matter. | |||
| {{See also|Weak interaction|Electroweak interaction}} | |||
| The weak interaction is responsible for various forms of ], such as ]. It is weak and short-range, due to the fact that the weak mediating particles, W and Z bosons, have mass. W bosons have electric charge and mediate interactions that change the particle type (referred to as flavor) and charge. Interactions mediated by W bosons are ]s. Z bosons are neutral and mediate neutral current interactions, which do not change particle flavor. Thus Z bosons are similar to the photon, aside from them being massive and interacting with the neutrino. The weak interaction is also the only interaction to violate ] and ]. Parity violation is maximal for charged current interactions, since the W boson interacts exclusively with left-handed fermions and right-handed antifermions. | |||
| In the Standard Model, the weak force is understood in terms of the electroweak theory, which states that the weak and electromagnetic interactions become united into a single ''electroweak'' interaction at high energies. | |||
| ==Tests and predictions== | |||
| {{Refimprove section|date=April 2008}} | |||
| The Standard Model (SM) predicted the existence of the ], ], and the ] and ]s before these particles were observed. Their predicted properties were experimentally confirmed with good precision. To give an idea of the success of the SM, the following table compares the measured masses of the W and Z bosons with the masses predicted by the SM: | |||
| === Strong nuclear force === | |||
| {| class="wikitable" | |||
| {{See also|Strong interaction|Nuclear force|Quantum chromodynamics}} | |||
| |- | |||
| The strong nuclear force is responsible for hadronic and ]. It is mediated by gluons, which couple to color charge. Since gluons themselves have color charge, the strong force exhibits ] and ]. Confinement means that only color-neutral particles can exist in isolation, therefore quarks can only exist in hadrons and never in isolation, at low energies. Asymptotic freedom means that the strong force becomes weaker, as the energy scale increases. The strong force overpowers the ] repulsion of protons and quarks in nuclei and hadrons respectively, at their respective scales. | |||
| ! Quantity !! Measured (GeV) !! SM prediction (GeV) | |||
| |- | |||
| | Mass of W boson || 80.387 ± 0.019 ||80.390 ± 0.018 | |||
| |- | |||
| | Mass of Z boson || 91.1876 ± 0.0021 || 91.1874 ± 0.0021 | |||
| |} | |||
| The SM also makes several predictions about the decay of Z bosons, which have been experimentally confirmed by the ] at ]. | |||
| While quarks are bound in hadrons by the fundamental strong interaction, which is mediated by gluons, nucleons are bound by an emergent phenomenon termed the ''residual strong force'' or '']''. This interaction is mediated by mesons, such as the ]. The color charges inside the nucleon cancel out, meaning most of the gluon and quark fields cancel out outside of the nucleon. However, some residue is "leaked", which appears as the exchange of virtual mesons, that causes the attractive force between nucleons. The (fundamental) strong interaction is described by quantum chromodynamics, which is a component of the Standard Model. | |||
| In May 2012 ] reported that their recently analyzed data may suggest possible flaws in the Standard Model of particle physics.<ref>.</ref><ref>BaBar Collaboration, ''Evidence for an excess of B -> D(*) Tau Nu decays'', .</ref> These data show that a particular type of particle decay called "B to D-star-tau-nu" happens more often than the Standard Model says it should. In this type of decay, a particle called the B-bar meson decays into a D meson, an antineutrino and a tau-lepton. | |||
| While the level of certainty of the excess (3.4 sigma) is not enough to claim a break from the Standard Model, the results are a potential sign of something amiss and are likely to impact existing theories, including those attempting to deduce the properties of ]s.<ref>.</ref> | |||
| == Tests and predictions == | |||
| On December 13, 2012, ] reported the constancy, over space and time, of a basic ] of nature that supports the ''standard model of physics''. The scientists, studying ] molecules in a distant ], found the change (∆μ/μ) in the ] μ to be equal to "(0.0 ± 1.0) × 10<sup>−7</sup> at ] z = 0.89" and consistent with "a ]".<ref name="Science-20121213">{{cite journal |last1=Bagdonaitel |first1=Julija |last2=Jensen |first2=Paul |last3=Henkel |first3=Christian |last4=Bethlem |first4=Hendrick L. |last5=Menten |first5=Karl M. |last6=Ubachs |first6=Wim |title=A Stringent Limit on a Drifting Proton-to-Electron Mass Ratio from Alcohol in the Early Universe |url=http://www.sciencemag.org/content/early/2012/12/12/science.1224898.abstract |date=December 13, 2012 |journal=] |doi=10.1126/science.1224898 |accessdate=December 14, 2012 |volume=339 |issue=6115 |pages=46 }}</ref><ref name="Space-20121213">{{cite web |last=Moskowitz |first=Clara |title=Phew! Universe's Constant Has Stayed Constant |url=http://www.space.com/18894-galaxy-alcohol-fundamental-constant.html |date=December 13, 2012 |publisher=] |accessdate=December 14, 2012 }}</ref> | |||
| The Standard Model predicted the existence of the ], ], ] and ], and predicted many of their properties before these particles were observed. The predictions were experimentally confirmed with good precision.<ref> | |||
| {{cite journal |last1=Woithe |first1=Julia |last2=Wiener |first2=Gerfried |last3=Van der Veken |first3=Frederik |title=Let's have a coffee with the Standard Model of particle physics! |journal=Phys. Educ. |volume=52 |issue= 3|pages=034001 |doi=10.1088/1361-6552/aa5b25 |year=2017 |bibcode=2017PhyEd..52c4001W |doi-access=free |url=http://cds.cern.ch/record/2807969/files/Woithe_2017_Phys._Educ._52_034001.pdf }}</ref> | |||
| The Standard Model also predicted the existence of the ], which was found in 2012 at the ], the final fundamental particle predicted by the Standard Model to be experimentally confirmed.<ref> | |||
| ==Challenges== | |||
| {{cite arXiv|eprint=1407.2122|last1=Altarelli|first1=Guido|title=The Higgs and the Excessive Success of the Standard Model|class=hep-ph|year=2014}}</ref> | |||
| == Challenges == | |||
| {{See also|Physics beyond the Standard Model}} | {{See also|Physics beyond the Standard Model}} | ||
| {{unsolved|physics| | {{unsolved|physics| | ||
| *What gives rise to the Standard Model of particle physics? | * What gives rise to the Standard Model of particle physics? | ||
| *Why do particle masses and ]s have the values that we measure? | * Why do particle masses and ]s have the values that we measure? | ||
| *Why are there three ] of particles? | * Why are there three ] of particles? | ||
| *Why is there more matter than ] in the universe? | * Why is there more matter than ] in the universe? | ||
| *Where does ] fit into the model? |
* Where does ] fit into the model? Does it even consist of one or more new particles? | ||
| }} | }} | ||
| Self-consistency of the Standard Model (currently formulated as a non-abelian gauge theory quantized through path-integrals) has not been mathematically proven. While regularized versions useful for approximate computations (for example ]) exist, it is not known whether they converge (in the sense of S-matrix elements) in the limit that the regulator is removed. A key question related to the consistency is the ] problem. | |||
| Self-consistency of the Standard Model (currently formulated as a non-] gauge theory quantized through path-integrals) has not been mathematically proved. While regularized versions useful for approximate computations (for example ]) exist, it is not known whether they converge (in the sense of S-matrix elements) in the limit that the regulator is removed. A key question related to the consistency is the ] problem. | |||
| Experiments indicate that ] have ], which the classic Standard Model did not allow.<ref>{{cite web|url=http://press.web.cern.ch/press/PressReleases/Releases2010/PR08.10E.html |title=CERN Press Release |publisher=Press.web.cern.ch |date=2010-05-31 |accessdate=2012-07-05}}</ref> To accommodate this finding, the classic Standard Model can be modified to include neutrino mass. | |||
| Experiments indicate that ] have ], which the classic Standard Model did not allow.<ref> | |||
| {{cite web | |||
| |date=31 May 2010 | |||
| |title=Particle chameleon caught in the act of changing | |||
| |url = http://press.cern/press-releases/2010/05/particle-chameleon-caught-act-changing | |||
| |publisher=] | |||
| |access-date=2016-11-12 | |||
| }}</ref> To accommodate this finding, the classic Standard Model can be modified to include neutrino mass, although it is not obvious exactly how this should be done. | |||
| If one insists on using only Standard Model particles, this can be achieved by adding a non-renormalizable interaction of leptons with the Higgs boson.<ref> | If one insists on using only Standard Model particles, this can be achieved by adding a non-renormalizable interaction of leptons with the Higgs boson.<ref> | ||
| {{cite journal | {{cite journal | ||
| |author= |
|author=S. Weinberg | ||
| |year= |
|year=1979 | ||
| |title= |
|title=Baryon and Lepton Nonconserving Processes | ||
| |journal=] | |||
| |volume=43 |issue=21 |pages=1566–1570 | |||
| |bibcode=1979PhRvL..43.1566W | |||
| |doi=10.1103/PhysRevLett.43.1566 | |||
| }}</ref> On a fundamental level, such an interaction emerges in the ] where heavy right-handed neutrinos are added to the theory. | |||
| This is natural in the ] extension of the Standard Model<ref name="Minkowski1977"> | |||
| {{cite journal | |||
| |author=P. Minkowski | |||
| |year=1977 | |||
| |title=μ → e γ at a Rate of One Out of 10<sup>9</sup> Muon Decays? | |||
| |journal=] | |||
| |volume=67 |issue=4 |pages=421–428 | |||
| |bibcode=1977PhLB...67..421M | |||
| |doi=10.1016/0370-2693(77)90435-X | |||
| }}</ref><ref name="MohapatraSenjanovic1980"> | |||
| {{cite journal | |||
| |author1=R.N. Mohapatra |author2=G. Senjanovic |year=1980 | |||
| |title=Neutrino Mass and Spontaneous Parity Nonconservation | |||
| |journal=] | |journal=] | ||
| |volume= |
|volume=44|issue=14|pages=912–915 | ||
| |bibcode = 1980PhRvL..44..912M | |||
| |doi= 10.1103/PhysRevLett.43.1566 | |||
| |doi=10.1103/PhysRevLett.44.912 | |||
| |issue= 21 | |||
| }}</ref> and in certain ].<ref name="Gell-Mann1979"> | |||
| }}</ref> On a fundamental level, such an interaction emerges in the ] where heavy right-handed neutrinos are added to the theory. | |||
| {{cite book | |||
| This is natural in the ] extension of the Standard Model <ref name="Minkowski1977">{{cite journal|author=P. Minkowski|doi=10.1016/0370-2693(77)90435-X|title=mu --> e gamma at a Rate of One Out of 1-Billion Muon Decays?|bibcode = 1977PhLB...67..421M|year=1977|journal=Physics Letters B|volume=67|issue=4|pages=421 }}</ref><ref name="MohapatraSenjanovic1980" >{{cite journal|journal=Phys. Rev. Lett.|volume=44|issue=14|pages=912–915|year=1980|author=R. N. Mohapatra, G. Senjanovic|doi=10.1103/PhysRevLett.44.912|title=Neutrino Mass and Spontaneous Parity Nonconservation|bibcode = 1980PhRvL..44..912M }}</ref> and in certain ].<ref name="Gell-Mann1979">M. Gell-Mann, P. Ramond and R. Slansky, in Supergravity, ed. by D. Freedman et al., North Holland (1979).</ref> As long as new physics appears below or around 10<sup>14</sup> ], the neutrino masses can be of the right order of magnitude. | |||
| |author1=M. Gell-Mann, P. Ramond |author2=R. Slansky | |||
| |name-list-style=amp |year=1979 | |||
| |pages=315–321 | |||
| |title=Supergravity | |||
| |editor1=F. van Nieuwenhuizen |editor2=D.Z. Freedman |publisher=] | |||
| |isbn=978-0-444-85438-4 | |||
| }}</ref> As long as new physics appears below or around 10<sup>14</sup> ], the neutrino masses can be of the right order of magnitude. | |||
| Theoretical and experimental research has attempted to extend the |
Theoretical and experimental research has attempted to extend the Standard Model into a ] or a ], a complete theory explaining all physical phenomena including constants. Inadequacies of the Standard Model that motivate such research include: | ||
| * |
* The model does not explain ], although physical confirmation of a theoretical particle known as a ] would account for it to a degree. Though it addresses strong and electroweak interactions, the Standard Model does not consistently explain the canonical theory of gravitation, ], in terms of ]. The reason for this is, among other things, that quantum field theories of gravity generally break down before reaching the ]. As a consequence, we have no reliable theory for the very early universe. | ||
| * Some consider it to be ''ad |
* Some physicists consider it to be ''ad hoc'' and inelegant, requiring 19 numerical constants whose values are unrelated and arbitrary.<ref name="BlumhoferHutter1997"> | ||
| {{cite journal | |||
| * The Higgs mechanism gives rise to the ] if any new physics (such as quantum gravity) is present at high energy scales. In order for the weak scale to be much smaller than the ], severe fine tuning of Standard Model parameters is required; | |||
| |author1=A. Blumhofer |author2=M. Hutter |year = 1997 | |||
| * It should be modified so as to be consistent with the emerging "Standard Model of ]." In particular, the Standard Model cannot explain the observed amount of ] (CDM) and gives contributions to ] which are many orders of magnitude too large. It is also difficult to accommodate the observed predominance of matter over antimatter (]/] ]). The ] and ] of the visible universe over large distances seems to require a mechanism like cosmic ], which would also constitute an extension of the Standard Model. | |||
| |title = Family Structure from Periodic Solutions of an Improved Gap Equation | |||
| |journal = Nuclear Physics | |||
| |volume = B484 | |||
| |issue=1 |pages = 80–96 | |||
| |doi = 10.1016/S0550-3213(96)00644-X | |||
| |bibcode = 1997NuPhB.484...80B | |||
| |arxiv = hep-ph/9605393 | |||
| }}</ref> Although the Standard Model, as it now stands, can explain why neutrinos have masses, the specifics of neutrino mass are still unclear. It is believed that explaining neutrino mass will require an additional 7 or 8 constants, which are also arbitrary parameters.<ref> | |||
| {{cite arXiv|eprint=hep-ph/0606054|last1=Strumia|first1=Alessandro|title=Neutrino masses and mixings and...|year=2006}}</ref> | |||
| * The Higgs mechanism gives rise to the ] if some new physics (coupled to the Higgs) is present at high energy scales. In these cases, in order for the weak scale to be much smaller than the ], severe fine tuning of the parameters is required; there are, however, other scenarios that include ] in which such fine tuning can be avoided.<ref> | |||
| {{cite journal |title=Agravity |journal=Journal of High Energy Physics|volume=2014 |issue=6 |page = 080 |url = http://inspirehep.net/record/1286134 |arxiv = 1403.4226 |bibcode = 2014JHEP...06..080S |doi=10.1007/JHEP06(2014)080|pmid = 31258400|pmc = 6560704|last1 = Salvio|first1 = Alberto|last2 = Strumia|first2 = Alessandro|year = 2018}}</ref> There are also issues of ], which suggests that it may not be possible to create a consistent quantum field theory involving elementary scalar particles.<ref name="TrivPurs"> | |||
| {{cite journal |author=D.J.E. Callaway |year=1988 | |||
| |title=Triviality Pursuit: Can Elementary Scalar Particles Exist? |journal=] | |||
| |volume=167 |issue=5 |pages=241–320 |doi=10.1016/0370-1573(88)90008-7 | |||
| |bibcode = 1988PhR...167..241C |author-link=David J E Callaway | |||
| }}</ref> | |||
| * The model is inconsistent with the emerging ] of cosmology. Contentions include the absence of an explanation in the Standard Model of particle physics for the observed amount of ] (CDM) and its contributions to ], which are many orders of magnitude too large. It is also difficult to accommodate the observed predominance of matter over antimatter (]/] ]). The ] and ] of the visible universe over large distances seems to require a mechanism like cosmic ], which would also constitute an extension of the Standard Model. | |||
| Currently, no proposed ] has been widely accepted or verified. | Currently, no proposed ] has been widely accepted or verified. | ||
| ==See also== | == See also == | ||
| {{ |
{{cols|colwidth=27em}} | ||
| * ] | |||
| {{Misplaced Pages books|Particles of the Standard Model}} | |||
| * ]: | |||
| ** ] | |||
| ** ]: ], ], ] | |||
| ** ]: ], ], ], ] | |||
| * ]: ] | |||
| * ] | |||
| * ]: ], ] | |||
| * ] | |||
| * Open questions: ], ]es, ], ] | |||
| * ] | |||
| * Standard Model: ], ] | |||
| * ] | |||
| {{colend}} | |||
| == Notes == | |||
| *]: | |||
| {{NoteFoot}} | |||
| **] | |||
| **]: ], ], ] | |||
| **]: ], ], ], ] | |||
| *]: ] | |||
| *] | |||
| *]: ], ] | |||
| *] | |||
| *] | |||
| *] | |||
| *Open questions: ], ], ]es, ] | |||
| *] | |||
| *] | |||
| *Standard Model: ], ] | |||
| *] | |||
| == References == | |||
| ==Notes and references== | |||
| {{reflist}} | |||
| {{Reflist|group=nb}} | |||
| == Further reading == | |||
| ==References== | |||
| * {{cite book | |||
| | last=Oerter | |||
| {{Reflist|colwidth=35em}} | |||
| | first=Robert | |||
| ==Further reading== | |||
| *{{cite book | |||
| | author=R. Oerter | |||
| | year=2006 | | year=2006 | ||
| | title=The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics | | title=The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics | ||
| | isbn=978-0-452-28786-0 | |||
| | publisher=] | |||
| | |
| publisher=Plume | ||
| }} | }} | ||
| *{{cite book | * {{cite book | ||
| | |
| last=Schumm | ||
| | first=Bruce A. | |||
| | year=2004 | | year=2004 | ||
| | title=Deep Down Things: |
| title=Deep Down Things: The Breathtaking Beauty of Particle Physics | ||
| | publisher= |
| publisher=Johns Hopkins University Press | ||
| | isbn=0-8018-7971- |
| isbn=978-0-8018-7971-5 | ||
| | url-access=registration | |||
| | url=https://archive.org/details/deepdownthingsbr00schu | |||
| }} | |||
| * {{cite web | |||
| |url = http://www.symmetrymagazine.org/standard-model/ | |||
| |title = The Standard Model of Particle Physics Interactive Graphic | |||
| }} | }} | ||
| === Introductory textbooks === | |||
| *{{cite book | * {{cite book | ||
| | |
| author1=I. Aitchison | ||
| | author2=A. Hey | |||
| | year=2003 | | year=2003 | ||
| | title=Gauge Theories in Particle Physics: A Practical Introduction. | | title=Gauge Theories in Particle Physics: A Practical Introduction. | ||
| | publisher= |
| publisher=Institute of Physics | ||
| | isbn=978-0-585-44550-2 | | isbn=978-0-585-44550-2 | ||
| }} | }} | ||
| *{{cite book | * {{cite book | ||
| | |
| author1=W. Greiner | ||
| | author2=B. Müller | |||
| | year=2000 | | year=2000 | ||
| | title=Gauge Theory of Weak Interactions | | title=Gauge Theory of Weak Interactions | ||
| | publisher= |
| publisher=Springer | ||
| | isbn=3-540-67672- |
| isbn=978-3-540-67672-0 | ||
| }} | |||
| *{{cite book | |||
| | author=G.D. Coughlan, J.E. Dodd, B.M. Gripaios | |||
| | year=2006 | |||
| | title=The Ideas of Particle Physics: An Introduction for Scientists | |||
| | publisher=] | |||
| | isbn= | |||
| }} | }} | ||
| *{{cite book | * {{cite book | ||
| | author1=J.E. Dodd | |||
| | author2=B.M. Gripaios | |||
| | year=2020 | |||
| | title=The Ideas of Particle Physics: An Introduction for Scientists | |||
| | publisher=Cambridge University Press | |||
| | isbn=978-1-108-72740-2}} | |||
| * {{cite book | |||
| | author=D.J. Griffiths | | author=D.J. Griffiths | ||
| | year=1987 | | year=1987 | ||
| | title=Introduction to Elementary Particles | | title=Introduction to Elementary Particles | ||
| | publisher= |
| publisher=John Wiley & Sons | ||
| | isbn=0-471-60386- |
| isbn=978-0-471-60386-3 | ||
| }} | }} | ||
| *{{cite book | * {{cite book | ||
| | author=G.L. Kane | | author=G.L. Kane | ||
| | year=1987 | | year=1987 | ||
| | title=Modern Elementary Particle Physics | | title=Modern Elementary Particle Physics | ||
| | publisher= |
| publisher=Perseus Books | ||
| | isbn=0-201-11749- |
| isbn=978-0-201-11749-3 | ||
| }} | }} | ||
| === Advanced textbooks === | |||
| *{{cite book | * {{cite book | ||
| | |
| author1=T.P. Cheng | ||
| | author2=L.F. Li | |||
| | year=2006 | | year=2006 | ||
| | title=Gauge theory of elementary particle physics | | title=Gauge theory of elementary particle physics | ||
| | publisher= |
| publisher=Oxford University Press | ||
| | isbn=0-19-851961- |
| isbn=978-0-19-851961-4 | ||
| }} Highlights the ] aspects of the Standard Model. | }} Highlights the ] aspects of the Standard Model. | ||
| *{{cite book | * {{cite book | ||
| | |
| author1=J.F. Donoghue | ||
| | author2=E. Golowich | |||
| | author3=B.R. Holstein | |||
| | year=1994 | | year=1994 | ||
| | title=Dynamics of the Standard Model | | title=Dynamics of the Standard Model | ||
| | publisher= |
| publisher=Cambridge University Press | ||
| | isbn=978-0-521-47652-2 | | isbn=978-0-521-47652-2 | ||
| }} Highlights dynamical and ] aspects of the Standard Model. | }} Highlights dynamical and ] aspects of the Standard Model. | ||
| *{{cite book | * {{cite book | ||
| | author=L. O'Raifeartaigh | | author=L. O'Raifeartaigh | ||
| | year=1988 | | year=1988 | ||
| | title=Group structure of gauge theories | | title=Group structure of gauge theories | ||
| | publisher= |
| publisher=Cambridge University Press | ||
| | isbn=0-521-34785- |
| isbn=978-0-521-34785-3 | ||
| }} | |||
| }} Highlights ] aspects of the Standard Model. | |||
| * {{cite book |url = https://books.google.com/books?id=QYlX6AL4CtwC |title=Elementary Particle Physics: Foundations of the Standard Model, Volume 2 |isbn=978-3-527-64890-0 |last1=Nagashima|first1=Yorikiyo|year=2013|publisher=Wiley}} 920 pages. | |||
| * {{cite book |url= https://books.google.com/books?id=HbdEAgAAQBAJ |title=Quantum Field Theory and the Standard Model |isbn=978-1-107-03473-0|last=Schwartz|first=Matthew D.|year=2014|publisher=Cambridge University}} 952 pages. | |||
| * {{cite book |url= https://books.google.com/books?id=dpANo3e_pS8C |title=The Standard Model and Beyond |isbn=978-1-4200-7907-4|last=Langacker|first=Paul|year=2009|publisher=CRC Press}} 670 pages. Highlights ] aspects of the Standard Model. | |||
| === Journal articles === | |||
| *{{cite journal | * {{cite journal | ||
| | |
|author1=E.S. Abers | ||
| |author2=B.W. Lee | |||
| |year=1973 | |year=1973 | ||
| |title=Gauge theories | |title=Gauge theories | ||
| |journal=] | |journal=] | ||
| |volume=9 |pages=1–141 | |volume=9 |issue=1 | ||
| |pages=1–141 | |||
| |doi=10.1016/0370-1573(73)90027-6 | |doi=10.1016/0370-1573(73)90027-6 | ||
| |bibcode = 1973PhR.....9....1A |
|bibcode = 1973PhR.....9....1A | ||
| }} | |||
| *{{cite |
* {{cite journal | ||
| |author=M. Baak |
|author=M. Baak |display-authors=etal | ||
| |year=2012 | |year=2012 | ||
| |title=The Electroweak Fit of the Standard Model after the Discovery of a New Boson at the LHC | |title=The Electroweak Fit of the Standard Model after the Discovery of a New Boson at the LHC | ||
| |journal=] | |||
| |class=hep-ph | |||
| |volume=72 |issue=11 |pages=2205 | |||
| |eprint=1209.2716v2 | |||
| |arxiv=1209.2716 | |||
| |last2=Goebel | |||
| |doi=10.1140/epjc/s10052-012-2205-9 | |||
| |first2=M. | |||
| |bibcode = 2012EPJC...72.2205B | |||
| |last3=Haller | |||
| |s2cid=15052448 | |||
| |first3=J. | |||
| |last4=Hoecker | |||
| |first4=A. | |||
| |last5=Kennedy | |||
| |first5=D. | |||
| |last6=Kogler | |||
| |first6=R. | |||
| |last7=Moenig | |||
| |first7=K. | |||
| |last8=Schott | |||
| |first8=M. | |||
| |last9=Stelzer | |||
| |first9=J. | |||
| }} | }} | ||
| *{{cite journal | * {{cite journal | ||
| |author=Y. Hayato |
|author=Y. Hayato |display-authors=etal | ||
| |year=1999 | |year=1999 | ||
| |title=Search for Proton Decay through ''p'' → ''νK''<sup>+</sup> in a Large Water Cherenkov Detector | |title=Search for Proton Decay through ''p'' → ''νK''<sup>+</sup> in a Large Water Cherenkov Detector | ||
| |journal=] | |journal=] | ||
| |volume=83 | |
|volume=83 |issue=8 |pages=1529–1533 | ||
| |arxiv = hep-ex/9904020 | |||
| |bibcode=1999PhRvL..83.1529H | |||
| |doi=10.1103/PhysRevLett.83.1529 | |doi=10.1103/PhysRevLett.83.1529 | ||
| |s2cid = 118326409}} | |||
| |bibcode=1999PhRvL..83.1529H | |||
| * {{cite arXiv | |||
| |arxiv = hep-ex/9904020 | |||
| |issue=8 | |||
| |last2=Earl | |||
| |first2=M. | |||
| |last3=Fukuda | |||
| |first3=Y. | |||
| |last4=Hayakawa | |||
| |first4=T. | |||
| |last5=Inoue | |||
| |first5=K. | |||
| |last6=Ishihara | |||
| |first6=K. | |||
| |last7=Ishino | |||
| |first7=H. | |||
| |last8=Itow | |||
| |first8=Y. | |||
| |last9=Kajita | |||
| |first9=T. }} | |||
| *{{cite arxiv | |||
| |author=S.F. Novaes | |author=S.F. Novaes | ||
| |year=2000 | |year=2000 | ||
| |title=Standard Model: An Introduction | |title=Standard Model: An Introduction | ||
| |class=hep-ph | |||
| |eprint=hep-ph/0001283 | |eprint=hep-ph/0001283 | ||
| }} | }} | ||
| *{{cite |
* {{cite arXiv | ||
| |author=D.P. Roy | |author=D.P. Roy | ||
| |year=1999 | |year=1999 | ||
| |title=Basic Constituents of Matter and their Interactions |
|title=Basic Constituents of Matter and their Interactions – A Progress Report | ||
| |class=hep-ph | |||
| |eprint=hep-ph/9912523 | |eprint=hep-ph/9912523 | ||
| }} | }} | ||
| *{{cite journal | * {{cite journal | ||
| |author=F. Wilczek | |author=F. Wilczek | ||
| |year=2004 | |year=2004 | ||
| |title=The Universe Is A Strange Place | |title=The Universe Is A Strange Place | ||
| |doi=10.1016/j.nuclphysbps.2004.08.001 | |doi=10.1016/j.nuclphysbps.2004.08.001 | ||
| |journal=Nuclear Physics B |
|journal=Nuclear Physics B: Proceedings Supplements | ||
| |volume=134 | |volume=134 | ||
| |page=3 | |page=3 | ||
| |arxiv=astro-ph/0401347 | |arxiv=astro-ph/0401347 | ||
| |bibcode = 2004NuPhS.134....3W |
|bibcode = 2004NuPhS.134....3W | ||
| |s2cid=28234516 | |||
| }} | |||
| ==External links== | == External links == | ||
| {{Commons}} | |||
| *"" omega tau podcast. | |||
| {{Wikiquote}} | |||
| *"" "]". | |||
| *"" |
* "" omega tau podcast. | ||
| * on the CERN website explains how the basic building blocks of matter interact, governed by four fundamental forces. | |||
| *"" at ]. | |||
| * , ] lectures (2010). | |||
| *"" After electroweak ], with no explicit ]. | |||
| *"" with explicit Higgs terms. PDF, PostScript, and LaTeX versions. | |||
| *"" Web tutorial. | |||
| *Nobes, Matthew (2002) "Introduction to the Standard Model of Particle Physics" on ]: | |||
| *"" The Standard Model on the CERN web site explains how the basic building blocks of matter interact, governed by four fundamental forces. | |||
| {{Clear}} | |||
| {{Standard model of physics}} | |||
| {{particles}} | {{particles}} | ||
| {{Quantum field theories}} | |||
| {{Physics-footer}} | {{Physics-footer}} | ||
| {{Portal bar|Mathematics|Physics}} | |||
| {{Use dmy dates|date=March 2011}} | |||
| {{Authority control}} | |||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
Latest revision as of 02:49, 20 January 2025
Theory of forces and subatomic particles This article is about a non-mathematical general overview of the Standard Model of particle physics. For a mathematical description, see Mathematical formulation of the Standard Model. For other uses, see Standard model (disambiguation).
The Standard Model of particle physics is the theory describing three of the four known fundamental forces (electromagnetic, weak and strong interactions – excluding gravity) in the universe and classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.
Although the Standard Model is believed to be theoretically self-consistent and has demonstrated some success in providing experimental predictions, it leaves some physical phenomena unexplained and so falls short of being a complete theory of fundamental interactions. For example, it does not fully explain why there is more matter than anti-matter, incorporate the full theory of gravitation as described by general relativity, or account for the universe's accelerating expansion as possibly described by dark energy. The model does not contain any viable dark matter particle that possesses all of the required properties deduced from observational cosmology. It also does not incorporate neutrino oscillations and their non-zero masses.
The development of the Standard Model was driven by theoretical and experimental particle physicists alike. The Standard Model is a paradigm of a quantum field theory for theorists, exhibiting a wide range of phenomena, including spontaneous symmetry breaking, anomalies, and non-perturbative behavior. It is used as a basis for building more exotic models that incorporate hypothetical particles, extra dimensions, and elaborate symmetries (such as supersymmetry) to explain experimental results at variance with the Standard Model, such as the existence of dark matter and neutrino oscillations.
Historical background
See also: History of quantum field theory, History of subatomic physics, Julian Schwinger, and John Clive WardIn 1928, Paul Dirac introduced the Dirac equation, which implied the existence of antimatter.
In 1954, Yang Chen-Ning and Robert Mills extended the concept of gauge theory for abelian groups, e.g. quantum electrodynamics, to nonabelian groups to provide an explanation for strong interactions. In 1957, Chien-Shiung Wu demonstrated parity was not conserved in the weak interaction.
In 1961, Sheldon Glashow combined the electromagnetic and weak interactions. In 1964, Murray Gell-Mann and George Zweig introduced quarks and that same year Oscar W. Greenberg implicitly introduced color charge of quarks. In 1967 Steven Weinberg and Abdus Salam incorporated the Higgs mechanism into Glashow's electroweak interaction, giving it its modern form.
In 1970, Sheldon Glashow, John Iliopoulos, and Luciano Maiani introduced the GIM mechanism, predicting the charm quark. In 1973 Gross and Wilczek and Politzer independently discovered that non-Abelian gauge theories, like the color theory of the strong force, have asymptotic freedom. In 1976, Martin Perl discovered the tau lepton at the SLAC. In 1977, a team led by Leon Lederman at Fermilab discovered the bottom quark.
The Higgs mechanism is believed to give rise to the masses of all the elementary particles in the Standard Model. This includes the masses of the W and Z bosons, and the masses of the fermions, i.e. the quarks and leptons.
After the neutral weak currents caused by Z boson exchange were discovered at CERN in 1973, the electroweak theory became widely accepted and Glashow, Salam, and Weinberg shared the 1979 Nobel Prize in Physics for discovering it. The W and Z bosons were discovered experimentally in 1983; and the ratio of their masses was found to be as the Standard Model predicted.
The theory of the strong interaction (i.e. quantum chromodynamics, QCD), to which many contributed, acquired its modern form in 1973–74 when asymptotic freedom was proposed (a development that made QCD the main focus of theoretical research) and experiments confirmed that the hadrons were composed of fractionally charged quarks.
The term "Standard Model" was introduced by Abraham Pais and Sam Treiman in 1975, with reference to the electroweak theory with four quarks. Steven Weinberg, has since claimed priority, explaining that he chose the term Standard Model out of a sense of modesty and used it in 1973 during a talk in Aix-en-Provence in France.
Particle content
The Standard Model includes members of several classes of elementary particles, which in turn can be distinguished by other characteristics, such as color charge.
All particles can be summarized as follows:
| Elementary particles | |||||||||||||||||||||||||||||
| Elementary fermionsHalf-integer spinObey the Fermi–Dirac statistics | Elementary bosonsInteger spinObey the Bose–Einstein statistics | ||||||||||||||||||||||||||||
| Quarks and antiquarksSpin = 1/2Have color chargeParticipate in strong interactions and electroweak interactions | Leptons and antileptonsSpin = 1/2No color chargeElectroweak interactions | Gauge bosonsSpin = 1Force carriers | Scalar bosonsSpin = 0 | ||||||||||||||||||||||||||
| Three generations | Three generations
| Three kinds
| One kind Higgs boson ( H ) | ||||||||||||||||||||||||||
Notes:
An anti-electron (
e
) is conventionally called a "positron".
Fermions
The Standard Model includes 12 elementary particles of spin 1⁄2, known as fermions. Fermions respect the Pauli exclusion principle, meaning that two identical fermions cannot simultaneously occupy the same quantum state in the same atom. Each fermion has a corresponding antiparticle, which are particles that have corresponding properties with the exception of opposite charges. Fermions are classified based on how they interact, which is determined by the charges they carry, into two groups: quarks and leptons. Within each group, pairs of particles that exhibit similar physical behaviors are then grouped into generations (see the table). Each member of a generation has a greater mass than the corresponding particle of generations prior. Thus, there are three generations of quarks and leptons. As first-generation particles do not decay, they comprise all of ordinary (baryonic) matter. Specifically, all atoms consist of electrons orbiting around the atomic nucleus, ultimately constituted of up and down quarks. On the other hand, second- and third-generation charged particles decay with very short half-lives and can only be observed in high-energy environments. Neutrinos of all generations also do not decay, and pervade the universe, but rarely interact with baryonic matter.
There are six quarks: up, down, charm, strange, top, and bottom. Quarks carry color charge, and hence interact via the strong interaction. The color confinement phenomenon results in quarks being strongly bound together such that they form color-neutral composite particles called hadrons; quarks cannot individually exist and must always bind with other quarks. Hadrons can contain either a quark-antiquark pair (mesons) or three quarks (baryons). The lightest baryons are the nucleons: the proton and neutron. Quarks also carry electric charge and weak isospin, and thus interact with other fermions through electromagnetism and weak interaction. The six leptons consist of the electron, electron neutrino, muon, muon neutrino, tau, and tau neutrino. The leptons do not carry color charge, and do not respond to strong interaction. The charged leptons carry an electric charge of −1 e, while the three neutrinos carry zero electric charge. Thus, the neutrinos' motions are influenced by only the weak interaction and gravity, making them difficult to observe.
Gauge bosons

The Standard Model includes 4 kinds of gauge bosons of spin 1, with bosons being quantum particles containing an integer spin. The gauge bosons are defined as force carriers, as they are responsible for mediating the fundamental interactions. The Standard Model explains the four fundamental forces as arising from the interactions, with fermions exchanging virtual force carrier particles, thus mediating the forces. At a macroscopic scale, this manifests as a force. As a result, they do not follow the Pauli exclusion principle that constrains fermions; bosons do not have a theoretical limit on their spatial density. The types of gauge bosons are described below.
- Electromagnetism: Photons mediate the electromagnetic force, responsible for interactions between electrically charged particles. The photon is massless and is described by the theory of quantum electrodynamics (QED).
- Strong Interactions: Gluons mediate the strong interactions, which binds quarks to each other by influencing the color charge, with the interactions being described in the theory of quantum chromodynamics (QCD). They have no mass, and there are eight distinct gluons, with each being denoted through a color-anticolor charge combination (e.g. red–antigreen). As gluons have an effective color charge, they can also interact amongst themselves.
- Weak Interactions: The
W
,
W
, and
Z
gauge bosons mediate the weak interactions between all fermions, being responsible for radioactivity. They contain mass, with the
Z
having more mass than the
W
. The weak interactions involving the
W
act only on left-handed particles and right-handed antiparticles. The
W
carries an electric charge of +1 and −1 and couples to the electromagnetic interaction. The electrically neutral
Z
boson interacts with both left-handed particles and right-handed antiparticles. These three gauge bosons along with the photons are grouped together, as collectively mediating the electroweak interaction. - Gravity: It is currently unexplained in the Standard Model, as the hypothetical mediating particle graviton has been proposed, but not observed. This is due to the incompatibility of quantum mechanics and Einstein's theory of general relativity, regarded as being the best explanation for gravity. In general relativity, gravity is explained as being the geometric curving of spacetime.
The Feynman diagram calculations, which are a graphical representation of the perturbation theory approximation, invoke "force mediating particles", and when applied to analyze high-energy scattering experiments are in reasonable agreement with the data. However, perturbation theory (and with it the concept of a "force-mediating particle") fails in other situations. These include low-energy quantum chromodynamics, bound states, and solitons. The interactions between all the particles described by the Standard Model are summarized by the diagrams on the right of this section.
Higgs boson
Main article: Higgs bosonThe Higgs particle is a massive scalar elementary particle theorized by Peter Higgs (and others) in 1964, when he showed that Goldstone's 1962 theorem (generic continuous symmetry, which is spontaneously broken) provides a third polarisation of a massive vector field. Hence, Goldstone's original scalar doublet, the massive spin-zero particle, was proposed as the Higgs boson, and is a key building block in the Standard Model. It has no intrinsic spin, and for that reason is classified as a boson with spin-0.
The Higgs boson plays a unique role in the Standard Model, by explaining why the other elementary particles, except the photon and gluon, are massive. In particular, the Higgs boson explains why the photon has no mass, while the W and Z bosons are very heavy. Elementary-particle masses and the differences between electromagnetism (mediated by the photon) and the weak force (mediated by the W and Z bosons) are critical to many aspects of the structure of microscopic (and hence macroscopic) matter. In electroweak theory, the Higgs boson generates the masses of the leptons (electron, muon, and tau) and quarks. As the Higgs boson is massive, it must interact with itself.
Because the Higgs boson is a very massive particle and also decays almost immediately when created, only a very high-energy particle accelerator can observe and record it. Experiments to confirm and determine the nature of the Higgs boson using the Large Hadron Collider (LHC) at CERN began in early 2010 and were performed at Fermilab's Tevatron until its closure in late 2011. Mathematical consistency of the Standard Model requires that any mechanism capable of generating the masses of elementary particles must become visible at energies above 1.4 TeV; therefore, the LHC (designed to collide two 7 TeV proton beams) was built to answer the question of whether the Higgs boson actually exists.
On 4 July 2012, two of the experiments at the LHC (ATLAS and CMS) both reported independently that they had found a new particle with a mass of about 125 GeV/c (about 133 proton masses, on the order of 10 kg), which is "consistent with the Higgs boson". On 13 March 2013, it was confirmed to be the searched-for Higgs boson.
Theoretical aspects
Main article: Mathematical formulation of the Standard ModelConstruction of the Standard Model Lagrangian
| Parameters of the Standard Model | |||||
|---|---|---|---|---|---|
| # | Symbol | Description | Renormalization scheme (point) |
Value | |
| 1 | me | Electron mass | 0.511 MeV | ||
| 2 | mμ | Muon mass | 105.7 MeV | ||
| 3 | mτ | Tau mass | 1.78 GeV | ||
| 4 | mu | Up quark mass | μMS = 2 GeV | 1.9 MeV | |
| 5 | md | Down quark mass | μMS = 2 GeV | 4.4 MeV | |
| 6 | ms | Strange quark mass | μMS = 2 GeV | 87 MeV | |
| 7 | mc | Charm quark mass | μMS = mc | 1.32 GeV | |
| 8 | mb | Bottom quark mass | μMS = mb | 4.24 GeV | |
| 9 | mt | Top quark mass | On shell scheme | 173.5 GeV | |
| 10 | θ12 | CKM 12-mixing angle | 13.1° | ||
| 11 | θ23 | CKM 23-mixing angle | 2.4° | ||
| 12 | θ13 | CKM 13-mixing angle | 0.2° | ||
| 13 | δ | CKM CP violation Phase | 0.995 | ||
| 14 | g1 or g' | U(1) gauge coupling | μMS = mZ | 0.357 | |
| 15 | g2 or g | SU(2) gauge coupling | μMS = mZ | 0.652 | |
| 16 | g3 or gs | SU(3) gauge coupling | μMS = mZ | 1.221 | |
| 17 | θQCD | QCD vacuum angle | ~0 | ||
| 18 | v | Higgs vacuum expectation value | 246 GeV | ||
| 19 | mH | Higgs mass | 125.09±0.24 GeV | ||
Technically, quantum field theory provides the mathematical framework for the Standard Model, in which a Lagrangian controls the dynamics and kinematics of the theory. Each kind of particle is described in terms of a dynamical field that pervades space-time. The construction of the Standard Model proceeds following the modern method of constructing most field theories: by first postulating a set of symmetries of the system, and then by writing down the most general renormalizable Lagrangian from its particle (field) content that observes these symmetries.
The global Poincaré symmetry is postulated for all relativistic quantum field theories. It consists of the familiar translational symmetry, rotational symmetry and the inertial reference frame invariance central to the theory of special relativity. The local SU(3) × SU(2) × U(1) gauge symmetry is an internal symmetry that essentially defines the Standard Model. Roughly, the three factors of the gauge symmetry give rise to the three fundamental interactions. The fields fall into different representations of the various symmetry groups of the Standard Model (see table). Upon writing the most general Lagrangian, one finds that the dynamics depends on 19 parameters, whose numerical values are established by experiment. The parameters are summarized in the table (made visible by clicking "show") above.
Quantum chromodynamics sector
Main article: Quantum chromodynamicsThe quantum chromodynamics (QCD) sector defines the interactions between quarks and gluons, which is a Yang–Mills gauge theory with SU(3) symmetry, generated by . Since leptons do not interact with gluons, they are not affected by this sector. The Dirac Lagrangian of the quarks coupled to the gluon fields is given by where is a three component column vector of Dirac spinors, each element of which refers to a quark field with a specific color charge (i.e. red, blue, and green) and summation over flavor (i.e. up, down, strange, etc.) is implied.
The gauge covariant derivative of QCD is defined by , where
- γ are the Dirac matrices,
- G
μ is the 8-component () SU(3) gauge field, - λ
are the 3 × 3 Gell-Mann matrices, generators of the SU(3) color group, - G
μν represents the gluon field strength tensor, and - gs is the strong coupling constant.
The QCD Lagrangian is invariant under local SU(3) gauge transformations; i.e., transformations of the form , where is 3 × 3 unitary matrix with determinant 1, making it a member of the group SU(3), and is an arbitrary function of spacetime.
Electroweak sector
Main article: Electroweak interactionThe electroweak sector is a Yang–Mills gauge theory with the symmetry group U(1) × SU(2)L, where the subscript sums over the three generations of fermions; , and are the left-handed doublet, right-handed singlet up type, and right handed singlet down type quark fields; and and are the left-handed doublet and right-handed singlet lepton fields.
The electroweak gauge covariant derivative is defined as , where
- Bμ is the U(1) gauge field,
- YW is the weak hypercharge – the generator of the U(1) group,
- W→μ is the 3-component SU(2) gauge field,
- →τL are the Pauli matrices – infinitesimal generators of the SU(2) group – with subscript L to indicate that they only act on left-chiral fermions,
- g' and g are the U(1) and SU(2) coupling constants respectively,
- () and are the field strength tensors for the weak isospin and weak hypercharge fields.
Notice that the addition of fermion mass terms into the electroweak Lagrangian is forbidden, since terms of the form do not respect U(1) × SU(2)L gauge invariance. Neither is it possible to add explicit mass terms for the U(1) and SU(2) gauge fields. The Higgs mechanism is responsible for the generation of the gauge boson masses, and the fermion masses result from Yukawa-type interactions with the Higgs field.
Higgs sector
Main article: Higgs mechanismIn the Standard Model, the Higgs field is an SU(2)L doublet of complex scalar fields with four degrees of freedom: where the superscripts + and 0 indicate the electric charge of the components. The weak hypercharge of both components is 1. Before symmetry breaking, the Higgs Lagrangian is where is the electroweak gauge covariant derivative defined above and is the potential of the Higgs field. The square of the covariant derivative leads to three and four point interactions between the electroweak gauge fields and and the scalar field . The scalar potential is given by where , so that acquires a non-zero Vacuum expectation value, which generates masses for the Electroweak gauge fields (the Higgs mechanism), and , so that the potential is bounded from below. The quartic term describes self-interactions of the scalar field .
The minimum of the potential is degenerate with an infinite number of equivalent ground state solutions, which occurs when . It is possible to perform a gauge transformation on such that the ground state is transformed to a basis where and . This breaks the symmetry of the ground state. The expectation value of now becomes where has units of mass and sets the scale of electroweak physics. This is the only dimensional parameter of the Standard Model and has a measured value of ~246 GeV/c.
After symmetry breaking, the masses of the W and Z are given by and , which can be viewed as predictions of the theory. The photon remains massless. The mass of the Higgs boson is . Since and are free parameters, the Higgs's mass could not be predicted beforehand and had to be determined experimentally.
Yukawa sector
The Yukawa interaction terms are: where , , and are 3 × 3 matrices of Yukawa couplings, with the mn term giving the coupling of the generations m and n, and h.c. means Hermitian conjugate of preceding terms. The fields and are left-handed quark and lepton doublets. Likewise, and are right-handed up-type quark, down-type quark, and lepton singlets. Finally is the Higgs doublet and is its charge conjugate state.
The Yukawa terms are invariant under the SU(2)L × U(1)Y gauge symmetry of the Standard Model and generate masses for all fermions after spontaneous symmetry breaking.
Fundamental interactions
Main article: Fundamental interactionThe Standard Model describes three of the four fundamental interactions in nature; only gravity remains unexplained. In the Standard Model, such an interaction is described as an exchange of bosons between the objects affected, such as a photon for the electromagnetic force and a gluon for the strong interaction. Those particles are called force carriers or messenger particles.
| Property/Interaction | Gravitation | Electroweak | Strong | ||
|---|---|---|---|---|---|
| Weak | Electromagnetic | Fundamental | Residual | ||
| Mediating particles | Not yet observed (Graviton hypothesised) |
W, W and Z | γ (photon) | Gluons | π, ρ and ω mesons |
| Affected particles | All particles | Left-handed fermions | Electrically charged | Quarks, gluons | Hadrons |
| Acts on | Stress–energy tensor | Flavor | Electric charge | Color charge | |
| Bound states formed | Planets, stars, galaxies, galaxy groups | — | Atoms, molecules | Hadrons | Atomic nuclei |
| Strength at the scale of quarks (relative to electromagnetism) |
10 (predicted) | 10 | 1 | 60 | Not applicable to quarks |
| Strength at the scale of protons/neutrons (relative to electromagnetism) |
10 (predicted) | 10 | 1 | Not applicable to hadrons |
20 |
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2021) (Learn how and when to remove this message) |
Gravity
See also: Quantum gravity and Gravity
Despite being perhaps the most familiar fundamental interaction, gravity is not described by the Standard Model, due to contradictions that arise when combining general relativity, the modern theory of gravity, and quantum mechanics. However, gravity is so weak at microscopic scales, that it is essentially unmeasurable. The graviton is postulated to be the mediating particle, but has not yet been proved to exist.
Electromagnetism
See also: Electromagnetism and Quantum electrodynamicsElectromagnetism is the only long-range force in the Standard Model. It is mediated by photons and couples to electric charge. Electromagnetism is responsible for a wide range of phenomena including atomic electron shell structure, chemical bonds, electric circuits and electronics. Electromagnetic interactions in the Standard Model are described by quantum electrodynamics.
Weak nuclear force
See also: Weak interaction and Electroweak interactionThe weak interaction is responsible for various forms of particle decay, such as beta decay. It is weak and short-range, due to the fact that the weak mediating particles, W and Z bosons, have mass. W bosons have electric charge and mediate interactions that change the particle type (referred to as flavor) and charge. Interactions mediated by W bosons are charged current interactions. Z bosons are neutral and mediate neutral current interactions, which do not change particle flavor. Thus Z bosons are similar to the photon, aside from them being massive and interacting with the neutrino. The weak interaction is also the only interaction to violate parity and CP. Parity violation is maximal for charged current interactions, since the W boson interacts exclusively with left-handed fermions and right-handed antifermions.
In the Standard Model, the weak force is understood in terms of the electroweak theory, which states that the weak and electromagnetic interactions become united into a single electroweak interaction at high energies.
Strong nuclear force
See also: Strong interaction, Nuclear force, and Quantum chromodynamicsThe strong nuclear force is responsible for hadronic and nuclear binding. It is mediated by gluons, which couple to color charge. Since gluons themselves have color charge, the strong force exhibits confinement and asymptotic freedom. Confinement means that only color-neutral particles can exist in isolation, therefore quarks can only exist in hadrons and never in isolation, at low energies. Asymptotic freedom means that the strong force becomes weaker, as the energy scale increases. The strong force overpowers the electrostatic repulsion of protons and quarks in nuclei and hadrons respectively, at their respective scales.
While quarks are bound in hadrons by the fundamental strong interaction, which is mediated by gluons, nucleons are bound by an emergent phenomenon termed the residual strong force or nuclear force. This interaction is mediated by mesons, such as the pion. The color charges inside the nucleon cancel out, meaning most of the gluon and quark fields cancel out outside of the nucleon. However, some residue is "leaked", which appears as the exchange of virtual mesons, that causes the attractive force between nucleons. The (fundamental) strong interaction is described by quantum chromodynamics, which is a component of the Standard Model.
Tests and predictions
The Standard Model predicted the existence of the W and Z bosons, gluon, top quark and charm quark, and predicted many of their properties before these particles were observed. The predictions were experimentally confirmed with good precision.
The Standard Model also predicted the existence of the Higgs boson, which was found in 2012 at the Large Hadron Collider, the final fundamental particle predicted by the Standard Model to be experimentally confirmed.
Challenges
See also: Physics beyond the Standard Model Unsolved problem in physics:- What gives rise to the Standard Model of particle physics?
- Why do particle masses and coupling constants have the values that we measure?
- Why are there three generations of particles?
- Why is there more matter than antimatter in the universe?
- Where does dark matter fit into the model? Does it even consist of one or more new particles?
Self-consistency of the Standard Model (currently formulated as a non-abelian gauge theory quantized through path-integrals) has not been mathematically proved. While regularized versions useful for approximate computations (for example lattice gauge theory) exist, it is not known whether they converge (in the sense of S-matrix elements) in the limit that the regulator is removed. A key question related to the consistency is the Yang–Mills existence and mass gap problem.
Experiments indicate that neutrinos have mass, which the classic Standard Model did not allow. To accommodate this finding, the classic Standard Model can be modified to include neutrino mass, although it is not obvious exactly how this should be done.
If one insists on using only Standard Model particles, this can be achieved by adding a non-renormalizable interaction of leptons with the Higgs boson. On a fundamental level, such an interaction emerges in the seesaw mechanism where heavy right-handed neutrinos are added to the theory. This is natural in the left-right symmetric extension of the Standard Model and in certain grand unified theories. As long as new physics appears below or around 10 GeV, the neutrino masses can be of the right order of magnitude.
Theoretical and experimental research has attempted to extend the Standard Model into a unified field theory or a theory of everything, a complete theory explaining all physical phenomena including constants. Inadequacies of the Standard Model that motivate such research include:
- The model does not explain gravitation, although physical confirmation of a theoretical particle known as a graviton would account for it to a degree. Though it addresses strong and electroweak interactions, the Standard Model does not consistently explain the canonical theory of gravitation, general relativity, in terms of quantum field theory. The reason for this is, among other things, that quantum field theories of gravity generally break down before reaching the Planck scale. As a consequence, we have no reliable theory for the very early universe.
- Some physicists consider it to be ad hoc and inelegant, requiring 19 numerical constants whose values are unrelated and arbitrary. Although the Standard Model, as it now stands, can explain why neutrinos have masses, the specifics of neutrino mass are still unclear. It is believed that explaining neutrino mass will require an additional 7 or 8 constants, which are also arbitrary parameters.
- The Higgs mechanism gives rise to the hierarchy problem if some new physics (coupled to the Higgs) is present at high energy scales. In these cases, in order for the weak scale to be much smaller than the Planck scale, severe fine tuning of the parameters is required; there are, however, other scenarios that include quantum gravity in which such fine tuning can be avoided. There are also issues of quantum triviality, which suggests that it may not be possible to create a consistent quantum field theory involving elementary scalar particles.
- The model is inconsistent with the emerging Lambda-CDM model of cosmology. Contentions include the absence of an explanation in the Standard Model of particle physics for the observed amount of cold dark matter (CDM) and its contributions to dark energy, which are many orders of magnitude too large. It is also difficult to accommodate the observed predominance of matter over antimatter (matter/antimatter asymmetry). The isotropy and homogeneity of the visible universe over large distances seems to require a mechanism like cosmic inflation, which would also constitute an extension of the Standard Model.
Currently, no proposed theory of everything has been widely accepted or verified.
See also
- Yang–Mills theory
- Fundamental interaction:
- Gauge theory: Introduction to gauge theory
- Generation
- Higgs mechanism: Higgs boson, Alternatives to the Standard Higgs Model
- Lagrangian
- Open questions: CP violation, Neutrino masses, QCD matter, Quantum triviality
- Quantum field theory
- Standard Model: Mathematical formulation of, Physics beyond the Standard Model
- Electron electric dipole moment
Notes
- There are mathematical issues regarding quantum field theories still under debate (see e.g. Landau pole), but the predictions extracted from the Standard Model by current methods applicable to current experiments are all self-consistent.
- Although nine color–anticolor combinations mathematically exist, gluons form color octet particles. As one color-symmetric combination is linear and forms a color singlet particles, there are eight possible gluons.
References
- R. Oerter (2006). The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics (Kindle ed.). Penguin Group. p. 2. ISBN 978-0-13-236678-6. Retrieved 28 March 2022.
- R. Mann (2010). "25". An Introduction to Particle Physics and the Standard Model. CRC Press. ISBN 978-1-4200-8298-2.
- Overbye, Dennis (11 September 2023). "Don't Expect a 'Theory of Everything' to Explain It All". The New York Times. Archived from the original on 11 September 2023. Retrieved 11 September 2023.
- Carroll, Sean M.; Rhoades, Zachary H.; Leven, Jon (2007). Dark Matter, Dark Energy: The Dark Side of the Universe. Guidebook Part 2. Chantilly, VA: The Teaching Company. p. 59. ISBN 978-1-59803-350-2. OCLC 288435552. Retrieved 28 March 2022.
...Standard Model of Particle Physics: The modern theory of elementary particles and their interactions ... It does not, strictly speaking, include gravity, although it's often convenient to include gravitons among the known particles of nature...
- Yang, C. N.; Mills, R. (1954). "Conservation of Isotopic Spin and Isotopic Gauge Invariance". Physical Review. 96 (1): 191–195. Bibcode:1954PhRv...96..191Y. doi:10.1103/PhysRev.96.191.
- Cho, Adrian (5 February 2021). "Postage stamp to honor female physicist who many say should have won the Nobel Prize".
- S.L. Glashow (1961). "Partial-symmetries of weak interactions". Nuclear Physics. 22 (4): 579–588. Bibcode:1961NucPh..22..579G. doi:10.1016/0029-5582(61)90469-2.
- Greenberg, Oscar Wallace (2009), Greenberger, Daniel; Hentschel, Klaus; Weinert, Friedel (eds.), "Color Charge Degree of Freedom in Particle Physics", Compendium of Quantum Physics, Berlin, Heidelberg: Springer, pp. 109–111, doi:10.1007/978-3-540-70626-7_32, ISBN 978-3-540-70626-7, retrieved 17 September 2024
- S. Weinberg (1967). "A Model of Leptons". Physical Review Letters. 19 (21): 1264–1266. Bibcode:1967PhRvL..19.1264W. doi:10.1103/PhysRevLett.19.1264.
- A. Salam (1968). N. Svartholm (ed.). Elementary Particle Physics: Relativistic Groups and Analyticity. Eighth Nobel Symposium. Stockholm: Almquvist and Wiksell. p. 367.
- F. Englert; R. Brout (1964). "Broken Symmetry and the Mass of Gauge Vector Mesons". Physical Review Letters. 13 (9): 321–323. Bibcode:1964PhRvL..13..321E. doi:10.1103/PhysRevLett.13.321.
- P.W. Higgs (1964). "Broken Symmetries and the Masses of Gauge Bosons". Physical Review Letters. 13 (16): 508–509. Bibcode:1964PhRvL..13..508H. doi:10.1103/PhysRevLett.13.508.
- G.S. Guralnik; C.R. Hagen; T.W.B. Kibble (1964). "Global Conservation Laws and Massless Particles". Physical Review Letters. 13 (20): 585–587. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.
- ^ Weinberg, S. (1 May 2004). "The making of the Standard Model". European Physical Journal C. 34 (1): 5–13. arXiv:hep-ph/0401010. Bibcode:2004EPJC...34....5W. doi:10.1140/epjc/s2004-01761-1. ISSN 1434-6052.
- "The Nobel Prize in Physics 1995". NobelPrize.org. Retrieved 17 September 2024.
- magazine, STANFORD (1 January 2015). "In Memoriam". stanfordmag.org. Retrieved 17 September 2024.
- "Inquiring Minds | Discoveries at Fermilab - The Bottom Quark". www.fnal.gov. Retrieved 17 September 2024.
- F.J. Hasert; et al. (1973). "Search for elastic muon-neutrino electron scattering". Physics Letters B. 46 (1): 121. Bibcode:1973PhLB...46..121H. doi:10.1016/0370-2693(73)90494-2.
- F.J. Hasert; et al. (1973). "Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment". Physics Letters B. 46 (1): 138. Bibcode:1973PhLB...46..138H. doi:10.1016/0370-2693(73)90499-1.
- F.J. Hasert; et al. (1974). "Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment". Nuclear Physics B. 73 (1): 1. Bibcode:1974NuPhB..73....1H. doi:10.1016/0550-3213(74)90038-8.
- D. Haidt (4 October 2004). "The discovery of the weak neutral currents". CERN Courier. Archived from the original on 20 May 2011. Retrieved 8 May 2008.
- Gaillard, Mary K.; Grannis, Paul D.; Sciulli, Frank J. (January 1999). "The Standard Model of Particle Physics". Reviews of Modern Physics. 71 (2): S96 – S111. arXiv:hep-ph/9812285. Bibcode:1999RvMPS..71...96G. doi:10.1103/RevModPhys.71.S96. S2CID 119012610.
- D.J. Gross; F. Wilczek (1973). "Ultraviolet behavior of non-abelian gauge theories". Physical Review Letters. 30 (26): 1343–1346. Bibcode:1973PhRvL..30.1343G. doi:10.1103/PhysRevLett.30.1343.
- H.D. Politzer (1973). "Reliable perturbative results for strong interactions" (PDF). Physical Review Letters. 30 (26): 1346–1349. Bibcode:1973PhRvL..30.1346P. doi:10.1103/PhysRevLett.30.1346. Archived (PDF) from the original on 19 July 2018.
- Dean Rickles (2014). A Brief History of String Theory: From Dual Models to M-Theory. Springer, p. 11 n. 22.
- Aubert, J.; et al. (1974). "Experimental Observation of a Heavy Particle J". Physical Review Letters. 33 (23): 1404–1406. Bibcode:1974PhRvL..33.1404A. doi:10.1103/PhysRevLett.33.1404.
- Augustin, J.; et al. (1974). "Discovery of a Narrow Resonance in ee Annihilation". Physical Review Letters. 33 (23): 1406–1408. Bibcode:1974PhRvL..33.1406A. doi:10.1103/PhysRevLett.33.1406.
- Pais, A.; Treiman, S. B. (1975). "How Many Charm Quantum Numbers are There?". Physical Review Letters. 35 (23): 1556–1559. Bibcode:1975PhRvL..35.1556P. doi:10.1103/PhysRevLett.35.1556.
- Cao, Tian Yu (1 October 2019). Conceptual Developments of 20th Century Field Theories. Cambridge University Press (published 1998). p. 320. Bibcode:2019code.book.....C. doi:10.1017/9781108566926. ISBN 978-1-108-56692-6. S2CID 243686857.
- A model is a representation of reality, whereas a theory is an explanation of reality; this Misplaced Pages article and some of the literature refers to the Standard Model as a theory.
- Weinberg, Steven (20 April 2010). "This World and the Universe". YouTube. Talks at Google. Retrieved 29 March 2022.
- "World Science Festival". YouTube. 2015. Retrieved 29 March 2022.
- "Q&A with Standard Bearer Steven Weinberg".
- ^ "The Standard Model". SLAC National Accelerator Laboratory. Archived from the original on 20 June 2006. Retrieved 18 January 2024.
- Eisert, Jens (22 January 2013). "Pauli Principle, Reloaded". Physics. 6 (4): 8. arXiv:1210.5531. doi:10.1103/PhysRevLett.110.040404. PMID 25166142.
- "What is antimatter?". Scientific American. 24 January 2002. Archived from the original on 31 March 2014. Retrieved 19 January 2024.
- ^ "Standard Model - ATLAS Physics Cheat Sheet" (PDF). ATLAS. CERN. Retrieved 19 January 2024.
- "Color Charge and Confinement". University of Pittsburgh. Archived from the original on 22 March 2002. Retrieved 8 January 2024.
- Lindon, Jack (2020). Particle Collider Probes of Dark Energy, Dark Matter and Generic Beyond Standard Model Signatures in Events With an Energetic Jet and Large Missing Transverse Momentum Using the ATLAS Detector at the LHC (PhD). CERN.
- Jaeger, Gregg (2021). "Exchange Forces in Particle Physics". Foundations of Physics. 51 (1): 13. Bibcode:2021FoPh...51...13J. doi:10.1007/s10701-021-00425-0. S2CID 231811425.
- Cahn, Robert N.; Goldbaher, Gerson (2010). "Quarks, gluons, and jets" (PDF). The Experimental Foundations of Particle Physics (2nd ed.). Cambridge University Press (published 31 August 2009). p. 306. ISBN 978-0521521475. Archived (PDF) from the original on 14 July 2012.
- Hooper, Dan (19 May 2022). "What is the Standard Model of particle physics, and why are scientists looking beyond it?". Astronomy Magazine. Retrieved 20 January 2024.
- Butterworth, Jon (1 June 2014). "Gravity versus the Standard Model". The Guardian. ISSN 0261-3077. Retrieved 20 January 2024.
- G.S. Guralnik (2009). "The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles". International Journal of Modern Physics A. 24 (14): 2601–2627. arXiv:0907.3466. Bibcode:2009IJMPA..24.2601G. doi:10.1142/S0217751X09045431. S2CID 16298371.
- B.W. Lee; C. Quigg; H.B. Thacker (1977). "Weak interactions at very high energies: The role of the Higgs-boson mass". Physical Review D. 16 (5): 1519–1531. Bibcode:1977PhRvD..16.1519L. doi:10.1103/PhysRevD.16.1519.
- "Huge $10 billion collider resumes hunt for 'God particle'". CNN. 11 November 2009. Retrieved 4 May 2010.
- "Observation of a New Particle with a Mass of 125 GeV". CERN. 4 July 2012. Retrieved 5 July 2012.
- D. Overbye (4 July 2012). "A New Particle Could Be Physics' Holy Grail". The New York Times. Retrieved 4 July 2012.
- "New results indicate that particle discovered at CERN is a Higgs boson". CERN. 14 March 2013. Retrieved 14 June 2020.
- "LHC experiments delve deeper into precision". CERN. 11 July 2017. Archived from the original on 14 July 2017. Retrieved 23 July 2017.
- Gregg Jaeger (2021). "The Elementary Particles of Quantum Fields". Entropy. 23 (11): 1416. Bibcode:2021Entrp..23.1416J. doi:10.3390/e23111416. PMC 8623095. PMID 34828114.
- "The Standard Model". CERN. 15 December 2023.
- "Standard Model of Particles and Interactions". jhu.edu. Johns Hopkins University. Archived from the original on 4 March 2016. Retrieved 18 August 2016.
- Ashtekar, Abhay (29 September 2005). "Gravity and the quantum". New Journal of Physics. 7: 198–198. arXiv:gr-qc/0410054. doi:10.1088/1367-2630/7/1/198. ISSN 1367-2630.
- Kuchař, Karel V. (31 July 2011). "TIME AND INTERPRETATIONS OF QUANTUM GRAVITY". International Journal of Modern Physics D. 20 (supp01): 3–86. doi:10.1142/S0218271811019347. ISSN 0218-2718.
- Carney, Daniel (2024). "Graviton detection and the quantization of gravity". Physical Review D. 109 (4). arXiv:2308.12988. doi:10.1103/PhysRevD.109.044009.
- "The Standard Model". CERN. 4 December 2023. Retrieved 17 December 2023.
- Woithe, Julia; Wiener, Gerfried; Van der Veken, Frederik (2017). "Let's have a coffee with the Standard Model of particle physics!" (PDF). Phys. Educ. 52 (3): 034001. Bibcode:2017PhyEd..52c4001W. doi:10.1088/1361-6552/aa5b25.
- Altarelli, Guido (2014). "The Higgs and the Excessive Success of the Standard Model". arXiv:1407.2122 .
- "Particle chameleon caught in the act of changing". CERN. 31 May 2010. Retrieved 12 November 2016.
- S. Weinberg (1979). "Baryon and Lepton Nonconserving Processes". Physical Review Letters. 43 (21): 1566–1570. Bibcode:1979PhRvL..43.1566W. doi:10.1103/PhysRevLett.43.1566.
- P. Minkowski (1977). "μ → e γ at a Rate of One Out of 10 Muon Decays?". Physics Letters B. 67 (4): 421–428. Bibcode:1977PhLB...67..421M. doi:10.1016/0370-2693(77)90435-X.
- R.N. Mohapatra; G. Senjanovic (1980). "Neutrino Mass and Spontaneous Parity Nonconservation". Physical Review Letters. 44 (14): 912–915. Bibcode:1980PhRvL..44..912M. doi:10.1103/PhysRevLett.44.912.
- M. Gell-Mann, P. Ramond & R. Slansky (1979). F. van Nieuwenhuizen & D.Z. Freedman (eds.). Supergravity. North Holland. pp. 315–321. ISBN 978-0-444-85438-4.
- A. Blumhofer; M. Hutter (1997). "Family Structure from Periodic Solutions of an Improved Gap Equation". Nuclear Physics. B484 (1): 80–96. arXiv:hep-ph/9605393. Bibcode:1997NuPhB.484...80B. doi:10.1016/S0550-3213(96)00644-X.
- Strumia, Alessandro (2006). "Neutrino masses and mixings and...". arXiv:hep-ph/0606054.
- Salvio, Alberto; Strumia, Alessandro (2018). "Agravity". Journal of High Energy Physics. 2014 (6): 080. arXiv:1403.4226. Bibcode:2014JHEP...06..080S. doi:10.1007/JHEP06(2014)080. PMC 6560704. PMID 31258400.
- D.J.E. Callaway (1988). "Triviality Pursuit: Can Elementary Scalar Particles Exist?". Physics Reports. 167 (5): 241–320. Bibcode:1988PhR...167..241C. doi:10.1016/0370-1573(88)90008-7.
Further reading
- Oerter, Robert (2006). The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics. Plume. ISBN 978-0-452-28786-0.
- Schumm, Bruce A. (2004). Deep Down Things: The Breathtaking Beauty of Particle Physics. Johns Hopkins University Press. ISBN 978-0-8018-7971-5.
- "The Standard Model of Particle Physics Interactive Graphic".
Introductory textbooks
- I. Aitchison; A. Hey (2003). Gauge Theories in Particle Physics: A Practical Introduction. Institute of Physics. ISBN 978-0-585-44550-2.
- W. Greiner; B. Müller (2000). Gauge Theory of Weak Interactions. Springer. ISBN 978-3-540-67672-0.
- J.E. Dodd; B.M. Gripaios (2020). The Ideas of Particle Physics: An Introduction for Scientists. Cambridge University Press. ISBN 978-1-108-72740-2.
- D.J. Griffiths (1987). Introduction to Elementary Particles. John Wiley & Sons. ISBN 978-0-471-60386-3.
- G.L. Kane (1987). Modern Elementary Particle Physics. Perseus Books. ISBN 978-0-201-11749-3.
Advanced textbooks
- T.P. Cheng; L.F. Li (2006). Gauge theory of elementary particle physics. Oxford University Press. ISBN 978-0-19-851961-4. Highlights the gauge theory aspects of the Standard Model.
- J.F. Donoghue; E. Golowich; B.R. Holstein (1994). Dynamics of the Standard Model. Cambridge University Press. ISBN 978-0-521-47652-2. Highlights dynamical and phenomenological aspects of the Standard Model.
- L. O'Raifeartaigh (1988). Group structure of gauge theories. Cambridge University Press. ISBN 978-0-521-34785-3.
- Nagashima, Yorikiyo (2013). Elementary Particle Physics: Foundations of the Standard Model, Volume 2. Wiley. ISBN 978-3-527-64890-0. 920 pages.
- Schwartz, Matthew D. (2014). Quantum Field Theory and the Standard Model. Cambridge University. ISBN 978-1-107-03473-0. 952 pages.
- Langacker, Paul (2009). The Standard Model and Beyond. CRC Press. ISBN 978-1-4200-7907-4. 670 pages. Highlights group-theoretical aspects of the Standard Model.
Journal articles
- E.S. Abers; B.W. Lee (1973). "Gauge theories". Physics Reports. 9 (1): 1–141. Bibcode:1973PhR.....9....1A. doi:10.1016/0370-1573(73)90027-6.
- M. Baak; et al. (2012). "The Electroweak Fit of the Standard Model after the Discovery of a New Boson at the LHC". The European Physical Journal C. 72 (11): 2205. arXiv:1209.2716. Bibcode:2012EPJC...72.2205B. doi:10.1140/epjc/s10052-012-2205-9. S2CID 15052448.
- Y. Hayato; et al. (1999). "Search for Proton Decay through p → νK in a Large Water Cherenkov Detector". Physical Review Letters. 83 (8): 1529–1533. arXiv:hep-ex/9904020. Bibcode:1999PhRvL..83.1529H. doi:10.1103/PhysRevLett.83.1529. S2CID 118326409.
- S.F. Novaes (2000). "Standard Model: An Introduction". arXiv:hep-ph/0001283.
- D.P. Roy (1999). "Basic Constituents of Matter and their Interactions – A Progress Report". arXiv:hep-ph/9912523.
- F. Wilczek (2004). "The Universe Is A Strange Place". Nuclear Physics B: Proceedings Supplements. 134: 3. arXiv:astro-ph/0401347. Bibcode:2004NuPhS.134....3W. doi:10.1016/j.nuclphysbps.2004.08.001. S2CID 28234516.
External links
- "The Standard Model explained in Detail by CERN's John Ellis" omega tau podcast.
- The Standard Model on the CERN website explains how the basic building blocks of matter interact, governed by four fundamental forces.
- Particle Physics: Standard Model, Leonard Susskind lectures (2010).
| Standard Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Background | 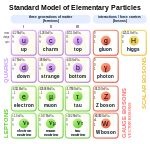 | ||||||||
| Constituents | |||||||||
| Beyond the Standard Model |
| ||||||||
| Experiments | |||||||||
| Particles in physics | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Elementary |
| ||||||||||||||||||||||||
| Composite |
| ||||||||||||||||||||||||
| Quasiparticles | |||||||||||||||||||||||||
| Lists | |||||||||||||||||||||||||
| Related | |||||||||||||||||||||||||
| Quantum field theories | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Theories | |||||||||||||||||
| Models |
| ||||||||||||||||
| Related |
| ||||||||||||||||
| See also: | |||||||||||||||||
| Major branches of physics | |
|---|---|
| Divisions | |
| Approaches | |
| Classical | |
| Modern | |
| Interdisciplinary | |
| Related | |

 . Since leptons do not interact with gluons, they are not affected by this sector. The Dirac Lagrangian of the quarks coupled to the gluon fields is given by
. Since leptons do not interact with gluons, they are not affected by this sector. The Dirac Lagrangian of the quarks coupled to the gluon fields is given by
 where
where  is a three component column vector of
is a three component column vector of  , where
, where
 ) SU(3) gauge field,
) SU(3) gauge field, , where
, where  is 3 × 3 unitary matrix with determinant 1, making it a member of the group SU(3), and
is 3 × 3 unitary matrix with determinant 1, making it a member of the group SU(3), and  is an arbitrary function of spacetime.
is an arbitrary function of spacetime.
 where the subscript
where the subscript  sums over the three generations of fermions;
sums over the three generations of fermions;  , and
, and  are the left-handed doublet, right-handed singlet up type, and right handed singlet down type quark fields; and
are the left-handed doublet, right-handed singlet up type, and right handed singlet down type quark fields; and  and
and  are the left-handed doublet and right-handed singlet lepton fields.
are the left-handed doublet and right-handed singlet lepton fields.
 , where
, where
 (
( ) and
) and  are the
are the  do not respect U(1) × SU(2)L gauge invariance. Neither is it possible to add explicit mass terms for the U(1) and SU(2) gauge fields. The Higgs mechanism is responsible for the generation of the gauge boson masses, and the fermion masses result from Yukawa-type interactions with the Higgs field.
do not respect U(1) × SU(2)L gauge invariance. Neither is it possible to add explicit mass terms for the U(1) and SU(2) gauge fields. The Higgs mechanism is responsible for the generation of the gauge boson masses, and the fermion masses result from Yukawa-type interactions with the Higgs field.
 where the superscripts + and 0 indicate the electric charge
where the superscripts + and 0 indicate the electric charge  of the components. The weak hypercharge
of the components. The weak hypercharge  of both components is 1. Before symmetry breaking, the Higgs Lagrangian is
of both components is 1. Before symmetry breaking, the Higgs Lagrangian is
 where
where  is the electroweak gauge covariant derivative defined above and
is the electroweak gauge covariant derivative defined above and  is the potential of the Higgs field. The square of the covariant derivative leads to three and four point interactions between the electroweak gauge fields
is the potential of the Higgs field. The square of the covariant derivative leads to three and four point interactions between the electroweak gauge fields  and
and  and the scalar field
and the scalar field  . The scalar potential is given by
. The scalar potential is given by
 where
where  , so that
, so that  , so that the potential is bounded from below. The quartic term describes self-interactions of the scalar field
, so that the potential is bounded from below. The quartic term describes self-interactions of the scalar field  . It is possible to perform a
. It is possible to perform a  and
and  . This breaks the symmetry of the ground state. The expectation value of
. This breaks the symmetry of the ground state. The expectation value of  where
where  has units of mass and sets the scale of electroweak physics. This is the only dimensional parameter of the Standard Model and has a measured value of ~246 GeV/c.
has units of mass and sets the scale of electroweak physics. This is the only dimensional parameter of the Standard Model and has a measured value of ~246 GeV/c.
 and
and  , which can be viewed as predictions of the theory. The photon remains massless. The mass of the
, which can be viewed as predictions of the theory. The photon remains massless. The mass of the  . Since
. Since  and
and  are free parameters, the Higgs's mass could not be predicted beforehand and had to be determined experimentally.
are free parameters, the Higgs's mass could not be predicted beforehand and had to be determined experimentally.
 where
where  ,
,  , and
, and  are 3 × 3 matrices of Yukawa couplings, with the mn term giving the coupling of the generations m and n, and h.c. means Hermitian conjugate of preceding terms. The fields
are 3 × 3 matrices of Yukawa couplings, with the mn term giving the coupling of the generations m and n, and h.c. means Hermitian conjugate of preceding terms. The fields  and
and  and
and  is its charge conjugate state.
is its charge conjugate state.