| Revision as of 22:37, 8 April 2014 editMpc755 (talk | contribs)231 edits Undid revision 603368136 by FyzixFighter (talk) - It is different than de Broglie-Bohm theory as de Broglie-Bohm theory is Bohmian mechanics which de Broglie was not a fan of. See Talk.← Previous edit | Latest revision as of 15:54, 8 December 2024 edit undoCitation bot (talk | contribs)Bots5,435,875 edits Added bibcode. | Use this bot. Report bugs. | Suggested by Dominic3203 | Linked from User:Chetvorno | #UCB_webform_linked 63/240 | ||
| (805 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{Short description|Physics experiment, showing light and matter can be modelled by both waves and particles}} | |||
| {{Redirect|Slit experiment||Diffraction}} | |||
| {{Redirect|Slit experiment||Slit experiment (disambiguation)}} | |||
| {{Use dmy dates|date=July 2013}} | |||
| {{Use dmy dates|date=November 2023}} | |||
| {{Quantum mechanics|cTopic=Experiments}} | |||
| {{multiple image | |||
| The '''double-slit experiment''' is a demonstration that light and matter can ] of both ] defined ]s and ]s; moreover, it displays the fundamentally probabilistic nature of ] phenomena. The experiment belongs to a general class of "double path" experiments, in which a wave is split into two separate waves that later combine back into a single wave. Changes in the path lengths of both waves result in a phase shift, creating an ]. Another version is the ], which splits the beam with a mirror. | |||
| | direction = vertical | |||
| | width = 251 | |||
| | image1 = Double-slit.svg | |||
| | caption1 = Photons or matter (like electrons) produce an interference pattern when two slits are used | |||
| | image2 = Young's slits.jpg | |||
| | caption2 = Light from a green laser passing through two slits 0.4 mm wide and 0.1 mm apart | |||
| }} | |||
| In ], the '''double-slit experiment''' demonstrates that light and matter can exhibit behavior of both classical ] and classical ]. This type of experiment was first performed by ] in 1801, as a demonstration of the wave behavior of visible light.<ref name="The Bakerian lecture">{{cite journal |last= Young |first= Thomas |title= The Bakerian lecture. Experiments and calculation relative to physical optics. |journal= Philosophical Transactions of the Royal Society of London |year= 1804 |volume= 94 |pages= 1–16 |doi= 10.1098/rstl.1804.0001 |s2cid= 110408369 |doi-access= free }}</ref> In 1927, ] and, independently, ] and his research student Alexander Reid<ref>{{Cite journal |last=Navarro |first=Jaume |date=2010 |title=Electron diffraction chez Thomson: early responses to quantum physics in Britain |url=https://www.cambridge.org/core/product/identifier/S0007087410000026/type/journal_article |journal=The British Journal for the History of Science |language=en |volume=43 |issue=2 |pages=245–275 |doi=10.1017/S0007087410000026 |issn=0007-0874 |s2cid=171025814}}</ref> demonstrated that electrons show the same behavior, which was later extended to atoms and molecules.<ref>{{Cite journal |last1=Thomson |first1=G. P. |last2=Reid |first2=A. |date=1927 |title=Diffraction of Cathode Rays by a Thin Film |journal=Nature |language=en |volume=119 |issue=3007 |page=890 |bibcode=1927Natur.119Q.890T |doi=10.1038/119890a0 |issn=0028-0836 |s2cid=4122313 |doi-access=free}}</ref><ref name="medium.com" /><ref name="Eibenberger 2013 pp. 14696–14700" /> Thomas Young's experiment with light was part of ] long before the development of quantum mechanics and the concept of ]. He believed it demonstrated that the ] ] was correct, and his experiment is sometimes referred to as ]<ref>While there is no doubt that Young's demonstration of optical interference, using sunlight, pinholes and cards, played a vital part in the acceptance of the wave theory of light, there is some question as to whether he ever actually performed a double-slit interference experiment. | |||
| *{{cite book |last= Robinson |first= Andrew |title= The Last Man Who Knew Everything |year= 2006 |publisher= Pi Press |location= New York, NY |isbn= 978-0-13-134304-7 |pages= |url= https://archive.org/details/lastmanwhoknewev00robi/page/123 }}</ref> or Young's slits.<ref>{{cite book|last=Kipnis|first=Naum S.|title= History of the Principle of Interference of Light|date=1991|publisher=Springer|page=65|isbn=978-0-8176-2316-6 |url=https://books.google.com/books?id=e7fvAAAAMAAJ}}</ref> | |||
| This experiment is sometimes referred to as ] and while there is no doubt that Young's demonstration of optical interference, using sunlight, pinholes and cards, played a vital part in the acceptance of the wave theory of light, there is some question as to whether he ever actually performed a double-slit interference experiment.<ref name=Robinson2006>{{cite book|last=Robinson|first=Andrew|title=The Last Man Who Knew Everything|year=2006|publisher=Pi Press|location=New York, NY|isbn=0-13-134304-1|pages=123–124}}</ref> | |||
| The experiment belongs to a general class of "double path" experiments, in which a wave is split into two separate waves (the wave is typically made of many photons and better referred to as a wave front, not to be confused with the wave properties of the individual photon) that later combine into a single wave. Changes in the path-lengths of both waves result in a ], creating an ]. Another version is the ], which splits the beam with a ].{{Quantum mechanics |cTopic=Experiments}} | |||
| In the basic version of this experiment, a ] such as a ] beam illuminates a plate pierced by two parallel slits, and the light passing through the slits is observed on a screen behind the plate.<ref name="Lederman">{{cite book | |||
| | last = Lederman | |||
| | first = Leon M. | |||
| | coauthors = Christopher T. Hill | |||
| | title = Quantum Physics for Poets | |||
| | publisher = Prometheus Books | |||
| | year = 2011 | |||
| | location = US | |||
| | pages = 102–111 | |||
| | url = http://books.google.com/books?id=qY_yOwHg_WYC&pg=PA102 | |||
| | doi = | |||
| | id = | |||
| | isbn = 1616142812}}</ref><ref name="Feynman">{{cite book | |||
| | last = Feynman | |||
| | first = Richard P. | |||
| | authorlink = | |||
| | coauthors = Robert B. Leighton, Matthew Sands | |||
| | title = The Feynman Lectures on Physics, Vol. 3 | |||
| | publisher = Addison-Wesley | |||
| | year = 1965 | |||
| | location = US | |||
| | pages = 1.1-1.8 | |||
| | url = | |||
| | doi = | |||
| | id = | |||
| | isbn = 0201021188}}</ref> The wave nature of light causes the light waves passing through the two slits to ], producing bright and dark bands on the screen—a result that would not be expected if light consisted of classical particles.<ref name="Lederman" /><ref>Feynman, 1965, p. 1.5</ref> However, the light is always found to be absorbed at the screen at discrete points, as individual particles (not waves), the interference pattern appearing via the varying density of these particle hits on the screen.<ref>{{cite web | |||
| | last = Darling | |||
| | first = David | |||
| | authorlink = David Darling (astronomer) | |||
| | title = Wave–Particle Duality | |||
| | work = The Internet Encyclopedia of Science | |||
| | publisher = The Worlds of David Darling | |||
| | year = 2007 | |||
| | url = http://www.daviddarling.info/encyclopedia/W/wave-particle_duality.html | |||
| | doi = | |||
| | accessdate = 2008-10-18}}</ref> Furthermore, versions of the experiment that include detectors at the slits find that each detected ] passes through one slit (as would a classical particle), but not through both slits (as would a wave).<ref>Feynman, 1965, p. 1.7</ref><ref></ref><ref name=" Müller-Kirsten">"''...if in a double-slit experiment, the detectors which register outcoming photons are placed immediately behind the diaphragm with two slits: A photon is registered in one detector, not in both...''" {{cite book | |||
| | last = Müller-Kirsten | |||
| | first = H. J. W. | |||
| | title = Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral | |||
| | publisher = World Scientific | |||
| | year = 2006 | |||
| | location = US | |||
| | pages = 14 | |||
| | url = http://books.google.com/books?id=p1_Z81Le58MC&pg=PA14 | |||
| | doi = | |||
| | id = | |||
| | isbn = 9812566910}}</ref><ref name="Plotnitsky">{{cite book | |||
| | last = Plotnitsky | |||
| | first = Arkady | |||
| | title = Niels Bohr and Complementarity: An Introduction | |||
| | publisher = Springer | |||
| | year = 2012 | |||
| | location = US | |||
| | pages = 75–76 | |||
| | url = http://books.google.com/books?id=dmdUp97S4AYC&pg=PA75 | |||
| | doi = | |||
| | id = | |||
| | isbn = 1461445175}}</ref><ref name="Rae">"''It seems that light passes through one slit or the other in the form of photons if we set up an experiment to detect which slit the photon passes, but passes through both slits in the form of a wave if we perform an interference experiment.''" {{cite book | |||
| | last = Rae | |||
| | first = Alastair I. M. | |||
| | title = Quantum Physics: Illusion Or Reality? | |||
| | publisher = Cambridge University Press | |||
| | year = 2004 | |||
| | location = UK | |||
| | pages = 9–10 | |||
| | url = http://books.google.com/books?id=FVtMqukQ6g4C&pg=PA9 | |||
| | doi = | |||
| | id = | |||
| | isbn = 1139455273}}</ref> These results demonstrate the principle of ]. | |||
| In the basic version of this experiment, a ], such as a ] beam, illuminates a plate pierced by two parallel slits, and the light passing through the slits is observed on a screen behind the plate.<ref name="Lederman">{{cite book |last= Lederman |first= Leon M. |author2=Christopher T. Hill |title= Quantum Physics for Poets |publisher= Prometheus Books |year= 2011 |location= US |pages= 102–111 |url= https://books.google.com/books?id=qY_yOwHg_WYC&pg=PA102 |isbn= 978-1-61614-281-0}}</ref><ref name="Feynman">{{cite book |last= Feynman |first= Richard P. |author2=Robert B. Leighton |author3= Matthew Sands |title= The Feynman Lectures on Physics, Vol. 3 | |||
| Other atomic-scale entities such as ] are found to exhibit the same behavior when fired toward a double slit.<ref name="Feynman" /> Additionally, the detection of individual discrete impacts is observed to be inherently probabilistic, which is inexplicable using ].<ref name="Feynman" /> | |||
| |publisher= Addison-Wesley |year= 1965 |pages= 1.1–1.8 |isbn= 978-0-201-02118-9|title-link= The Feynman Lectures on Physics }}</ref> The wave nature of light causes the light waves passing through the two slits to ], producing bright and dark bands on the screen – a result that would not be expected if light consisted of classical particles.<ref name="Lederman" /><ref>Feynman, 1965, p. 1.5</ref> However, the light is always found to be absorbed at the screen at discrete points, as individual particles (not waves); the interference pattern appears via the varying density of these particle hits on the screen.<ref>{{cite encyclopedia |last= Darling |first= David |author-link= David Darling (astronomer) |title= Wave–Particle Duality |encyclopedia= The Internet Encyclopedia of Science | |||
| |publisher= The Worlds of David Darling | year= 2007 |url= http://www.daviddarling.info/encyclopedia/W/wave-particle_duality.html |access-date= 18 October 2008}}</ref> Furthermore, versions of the experiment that include detectors at the slits find that each detected ] passes through one slit (as would a classical particle), and not through both slits (as would a wave).<ref>Feynman, 1965, p. 1.7</ref><ref>{{cite book|author1=Leon Lederman|author2=Christopher T. Hill|title=Quantum Physics for Poets|url=https://books.google.com/books?id=qY_yOwHg_WYC&pg=PA109|publisher=Prometheus Books, Publishers|isbn=978-1-61614-281-0|page=109|date=27 September 2011}}</ref><ref name="Müller-Kirsten">"''...if in a double-slit experiment, the detectors which register outcoming photons are placed immediately behind the diaphragm with two slits: A photon is registered in one detector, not in both...''" {{cite book |last= Müller-Kirsten |first= H. J. W. |title= Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral |publisher= World Scientific |year= 2006 |location= US |page=14 |url= https://books.google.com/books?id=p1_Z81Le58MC&pg=PA14 |isbn= 978-981-2566911}}</ref><ref name="Plotnitsky">{{cite book |last= Plotnitsky |first= Arkady |title= Niels Bohr and Complementarity: An Introduction |publisher= Springer |year= 2012 |location= US |pages= 75–76 |url= https://books.google.com/books?id=dmdUp97S4AYC&pg=PA75 |isbn= 978-1-4614-4517-3}}</ref><ref name="Rae">"''It seems that light passes through one slit or the other in the form of photons if we set up an experiment to detect which slit the photon passes, but passes through both slits in the form of a wave if we perform an interference experiment.''" {{cite book |last=Rae |first= Alastair I.M. |title= Quantum Physics: Illusion Or Reality? |publisher= Cambridge University Press |year= 2004 |location= UK |pages = 9–10 |url= https://books.google.com/books?id=FVtMqukQ6g4C&pg=PA9 |isbn= 978-1-139-45527-5}}</ref> However, ] demonstrate that particles do not form the interference pattern if one detects which slit they pass through. These results demonstrate the principle of ].<ref>Feynman, '']'', '''3''':Quantum Mechanics p.1-1 "There is one lucky break, however— electrons behave just like light".</ref><ref>See: ] {{cite journal |year= 1928 |title= The diffraction of electrons by a crystal of nickel |journal= ] |volume=7 |pages= 90–105 |doi= 10.1002/j.1538-7305.1928.tb00342.x|last1= Davisson |first1= C. J }}</ref> | |||
| Other atomic-scale entities, such as ], are found to exhibit the same behavior when fired towards a double slit.<ref name="Feynman" /> Additionally, the detection of individual discrete impacts is observed to be inherently probabilistic, which is inexplicable using ].<ref name="Feynman" /> | |||
| The experiment can be done with entities much larger than electrons and photons, although it becomes more difficult as size increases. The largest entities for which the double-slit experiment has been performed were molecules that each comprised 810 atoms (whose total mass was over 10,000 ]).<ref name="medium.com">""</ref><ref name="Eibenberger 2013 pp. 14696–14700">{{cite journal | |||
| | last =Eibenberger | |||
| The experiment can be done with entities much larger than electrons and photons, although it becomes more difficult as size increases. The largest entities for which the double-slit experiment has been performed were ]s that each comprised 2000 atoms (whose total mass was 25,000 ]).<ref name="Yaakov Y. Fein 1242–1245">{{cite journal |title=Quantum superposition of molecules beyond 25 kDa |author=Yaakov Y. Fein |author2=Philipp Geyer |author3=Patrick Zwick |author4=Filip Kiałka |author5=Sebastian Pedalino |author6=Marcel Mayor |author7=Stefan Gerlich |author8=Markus Arndt |journal=Nature Physics |volume=15 |pages=1242–1245 |date=September 2019 |issue=12 |doi=10.1038/s41567-019-0663-9|bibcode=2019NatPh..15.1242F |s2cid=203638258 }}</ref> | |||
| | first =Sandra | |||
| | coauthors =et al. | |||
| The double-slit experiment (and its variations) has become a classic for its clarity in expressing the central puzzles of quantum mechanics. ] called it "a phenomenon which is impossible to explain in any ], and which has in it the heart of quantum mechanics. In reality, it contains the only mystery ."<ref name="Feynman" /> | |||
| | title =Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu | |||
| | journal =] | |||
| | volume =15 | |||
| | pages =pp. 14696–14700 | |||
| | year =2013 | |||
| | url =http://arxiv.org/abs/1310.8343 | |||
| | doi =10.1039/C3CP51500A | |||
| }}</ref> | |||
| ==Overview== | ==Overview== | ||
| ] (the faint spots on either side of the main band) forms due to the nonzero width of the slit. |
] (the faint spots on either side of the main band) forms due to the nonzero width of the slit. This diffraction pattern is also seen in the double-slit image, but with many smaller interference fringes.]] | ||
| If light consisted strictly of ordinary or ] particles, and these particles were fired in a straight line through a slit and allowed to strike a screen on the other side, we would expect to see a pattern corresponding to the size and shape of the slit. However, when this "single-slit experiment" is actually performed, the pattern on the screen is a ] in which the light is spread out. The smaller the slit, the greater the angle of spread. The top portion of the image |
If light consisted strictly of ordinary or ] particles, and these particles were fired in a straight line through a slit and allowed to strike a screen on the other side, we would expect to see a pattern corresponding to the size and shape of the slit. However, when this "single-slit experiment" is actually performed, the pattern on the screen is a ] in which the light is spread out. The smaller the slit, the greater the angle of spread. The top portion of the image shows the central portion of the pattern formed when a red laser illuminates a slit and, if one looks carefully, two faint side bands. More bands can be seen with a more highly refined apparatus. ] explains the pattern as being the result of the interference of light waves from the slit. | ||
| If one illuminates two parallel slits, the light from the two slits again interferes. Here the interference is a more pronounced pattern with a series of alternating light and dark bands. The width of the bands is a property of the frequency of the illuminating light.<ref>] first proposed the use of this effect as an artifact-independent reference standard for ] | |||
| Similarly, if light consisted strictly of classical particles and we illuminated two parallel slits, the expected pattern on the screen would simply be the sum of the two single-slit patterns. In reality, however, the pattern changes to one with a series of light and dark bands (See the bottom photograph to the right.) When ] (1773–1829) first demonstrated this phenomenon, it indicated that light consists of waves, as the distribution of brightness can be explained by the alternately additive and subtractive interference of ]s.<ref name="Feynman" >{{cite book | last = Feynman | first = Richard P. | authorlink = Richard Feynman | coauthors = Robert Leighton, Matthew Sands | title = ], Volume III | publisher = Addison-Wesley | year = 1965 | location = Massachusetts, USA | |||
| *C.S. Peirce (July 1879). "Note on the Progress of Experiments for Comparing a Wave-length with a Meter". ''American Journal of Science'', as referenced by Crease, Robert P. (2011). ''World in the Balance: The historic quest for an absolute system of measurement''. New York: W.W. Norton. p. 317. {{ISBN|978-0-393-07298-3}}. p. 203.</ref> (See the bottom photograph to the right.) | |||
| | pages = 1–1 to 1–9 | isbn = 0-201-02118-8P}}</ref> Young's experiment, performed in the early 1800s, played a vital part in the acceptance of the wave theory of light, vanquishing the ] proposed by ], which had been the accepted model of light propagation in the 17th and 18th centuries. However, the later discovery of the ] demonstrated that under different circumstances, light can behave as if it is composed of discrete particles. These seemingly contradictory discoveries made it necessary to go beyond classical physics and take the ] nature of light into account. | |||
| ] | |||
| The double-slit experiment (and its variations) has become a classic ], for its clarity in expressing the central puzzles of quantum mechanics. Because it demonstrates the fundamental limitation of the ability of the observer to predict experimental results, ] called it "a phenomenon which is impossible to explain in any ], and which has in it the heart of quantum mechanics. In reality, it contains the ''only'' mystery ."<ref name="Feynman" /> Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment.<ref name="Greene_1999">{{cite book|last =Greene|first =Brian|authorlink =Brian Greene|title =] |publisher =W.W. Norton|location =New York|year =1999|pages = 97–109|isbn =0-393-04688-5 }}</ref> ] and ] have succinctly expressed this limitation as follows: | |||
| When ] (1773–1829) first demonstrated this phenomenon, it indicated that light consists of waves, as the distribution of brightness can be explained by the alternately additive and subtractive interference of ]s.<ref name="Feynman" /> Young's experiment, performed in the early 1800s, played a crucial role in the understanding of the wave theory of light, vanquishing the ] proposed by ], which had been the accepted model of light propagation in the 17th and 18th centuries. | |||
| However, the later discovery of the ] demonstrated that under different circumstances, light can behave as if it is composed of discrete particles. These seemingly contradictory discoveries made it necessary to go beyond classical physics and take into account the ] nature of light. | |||
| <blockquote>The observer can decide whether or not to put detectors into the interfering path. That way, by deciding whether or not to determine the path through the two-slit experiment, he can decide which property can become reality. If he chooses not to put the detectors there, then the interference pattern will become reality; if he does put the detectors there, then the beam path will become reality. Yet, most importantly, the observer has no influence on the specific element of the world which becomes reality. Specifically, if he chooses to determine the path, he has no influence whatsoever which of the two paths, the left one or the right one, Nature will tell him is the one where the particle is found. Likewise, if he chooses to observe the interference pattern he has no influence whatsoever where in the observation plane he will observe a specific particle. Both outcomes are completely random.<ref name=Brukner-Zeilinger>{{cite journal | author = Brukner C, Zeilinger A | year = 2002 | title = Young’s experiment and the finiteness of information | journal = Philosophical Transactions of the Royal Society | volume = 360 | pages = 1061–1069 }}</ref></blockquote> | |||
| Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment.<ref name="Greene_1999">{{cite book |last= Greene |first= Brian |author-link= Brian Greene |title= The Elegant Universe: Super Strings, Hidden Dimensions, and the Quest for the Ultimate Theory |publisher= W.W. Norton |location= New York |year= 1999 |pages= |isbn= 978-0-393-04688-5 |url= https://archive.org/details/elegantuniverses0000gree/page/97 }}</ref> He also proposed (as a thought experiment) that if detectors were placed before each slit, the interference pattern would disappear.<ref>Feynman, 1965, chapter 3</ref> | |||
| The ] provides a detailed treatment of the mathematics of double-slit interference in the context of quantum mechanics. | The ] provides a detailed treatment of the mathematics of double-slit interference in the context of quantum mechanics. | ||
| A low-intensity double-slit experiment was first performed by ] in 1909,<ref> |
A low-intensity double-slit experiment was first performed by ] in 1909,<ref>{{cite journal | ||
| | first1=G. I. |last1=Taylor | authorlink1=Geoffrey Ingram Taylor | |||
| | title=Interference Fringes with Feeble Light | |||
| | journal = ] | |||
| | volume=15 | |||
| | page=114 | |||
| | date=1909 | |||
| | url=https://archive.org/details/proceedingsofcam15190810camb/page/114/mode/2up | access-date=7 December 2024}}</ref> by reducing the level of incident light until photon emission/absorption events were mostly non-overlapping. | |||
| {{Anchor|Claus Jönsson}} | {{Anchor|Claus Jönsson}} | ||
| A slit interference experiment was not performed with anything other than light until 1961, when ] of the ] performed it with coherent electron beams and multiple slits.<ref>{{Cite journal|last=Jönsson|first=Claus|date=1 August 1961|title=Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten|journal=Zeitschrift für Physik|language=de|volume=161|issue=4|pages=454–474|doi=10.1007/BF01342460|issn=0044-3328|bibcode = 1961ZPhy..161..454J |s2cid=121659705}}</ref><ref>{{Cite journal|last=Jönsson|first=Claus|date=1 January 1974|title=Electron Diffraction at Multiple Slits|journal=American Journal of Physics|volume=42|issue=1|pages=4–11|doi=10.1119/1.1987592|issn=0002-9505|bibcode = 1974AmJPh..42....4J }}</ref> In 1974, the Italian physicists Pier Giorgio Merli, Gian Franco Missiroli, and ] performed a related experiment using single electrons from a coherent source and a biprism beam splitter, showing the statistical nature of the buildup of the interference pattern, as predicted by quantum theory.<ref>{{cite journal |last1= Merli |first1= P G |last2= Missiroli |first2= G F |last3= Pozzi |first3= G |year= 1976 |title= On the statistical aspect of electron interference phenomena |journal= American Journal of Physics |volume= 44 |issue= 3|pages= 306–307 |doi= 10.1119/1.10184 |bibcode = 1976AmJPh..44..306M}}</ref><ref>{{cite journal |last1= Rosa |first1= R |year= 2012 |title= The Merli–Missiroli–Pozzi Two-Slit Electron-Interference Experiment |journal = Physics in Perspective |volume= 14 |issue= 2| pages= 178–194 |doi= 10.1007/s00016-011-0079-0 |pmid= 26525832 |pmc= 4617474 |bibcode = 2012PhP....14..178R }}</ref> In 2002, the single-electron version of the experiment was voted "the most beautiful experiment" by readers of ''].''<ref>. Physics World 2002 {{Webarchive|url=https://web.archive.org/web/20210524080643/https://physicsworld.com/a/the-double-slit-experiment/ |date=24 May 2021 }}</ref> Since that time a number of related experiments have been published, with a little controversy.<ref>{{Cite journal |last1=Steeds |first1=John |last2=Merli |first2=Pier Giorgio |last3=Pozzi |first3=Giulio |last4=Missiroli |first4=GianFranco |last5=Tonomura |first5=Akira |date=2003 |title=The double-slit experiment with single electrons |url=https://iopscience.iop.org/article/10.1088/2058-7058/16/5/24 |journal=Physics World |volume=16 |issue=5 |pages=20–21 |doi=10.1088/2058-7058/16/5/24 |issn=0953-8585}}</ref> | |||
| A double-slit experiment was not performed with anything other than light until 1961, when ] of the ] performed it with electrons.<ref>Jönsson C,(1961) ''Zeitschrift für Physik'', '''161''':454–474 {{doi|10.1007/BF01342460}}</ref><ref>Jönsson C (1974). Electron diffraction at multiple slits. ''American Journal of Physics'', '''42''':4–11 {{doi|10.1119/1.1987592}}.</ref> In 2002, Jönsson's double-slit experiment was voted "the most beautiful experiment" by readers of ''].''<ref>. Physics World 2002.</ref> | |||
| In 2012, Stefano Frabboni and co-workers sent single electrons onto nanofabricated slits (about 100 nm wide) and, by detecting the transmitted electrons with a single-electron detector, they could show the build-up of a double-slit interference pattern.<ref>{{Cite journal|last1=Frabboni|first1=Stefano|last2=Gabrielli|first2=Alessandro|last3=Carlo Gazzadi|first3=Gian|last4=Giorgi|first4=Filippo|last5=Matteucci|first5=Giorgio|last6=Pozzi|first6=Giulio|last7=Cesari|first7=Nicola Semprini|last8=Villa|first8=Mauro|last9=Zoccoli|first9=Antonio|date=May 2012|title=The Young-Feynman two-slits experiment with single electrons: Build-up of the interference pattern and arrival-time distribution using a fast-readout pixel detector|journal=Ultramicroscopy|volume=116|pages=73–76|doi=10.1016/j.ultramic.2012.03.017|issn=0304-3991}}</ref> Many related experiments involving the coherent interference have been performed; they are the basis of modern electron diffraction, microscopy and high resolution imaging.<ref>{{Cite book |last=Cowley |first=J. M. |title=Diffraction physics |date=1995 |publisher=Elsevier |isbn=978-0-444-82218-5 |edition=3rd |series=North Holland personal library |location=Amsterdam}}</ref><ref>{{Cite book |last=Spence |first=John C. H. |title=High-resolution electron microscopy |date=2017 |publisher=Oxford University Press |isbn=978-0-19-879583-4 |edition=Fourth edition, first published in paperback |location=Oxford}}</ref> | |||
| The appearance of interference built up from individual photons could seemingly be explained by assuming that a single photon has its own associated wavefront that passes through both slits, and that the single photon will show up on the detector screen according to the net probability values resulting from the co-incidence of the two probability waves coming by way of the two slits.<ref>de Broglie, Louis (1953). ''The Revolution in Physics; a Non-Mathematical Survey of Quanta''. Translated by Ralph W. Niemeyer. New York: Noonday Press. pp. 47, 117, 178–186.</ref> However, more complicated systems that involve two or more particles in superposition are not amenable to such a simple, classically intuitive explanation.<ref>Baggott, Jim (2011). ''The Quantum Story: A History in 40 Moments''. New York: Oxford University Press. pp. 76. ("The wavefunction of a system containing ''N'' particles depends on 3''N'' position coordinates and is a function in a 3''N''-dimensional configuration space or 'phase space'. It is difficult to visualize a reality comprising imaginary functions in an abstract, multi-dimensional space. No difficulty arises, however, if the imaginary functions are not to be given a real interpretation.")</ref> | |||
| In 2018, single particle interference was demonstrated for antimatter in the (L-NESS, ]) of Rafael Ferragut<!--Q53261781--> in ] (]), by a group led by Marco Giammarchi.<ref>{{cite journal | doi = 10.1126/sciadv.aav7610 | volume=5 | title=First demonstration of antimatter wave interferometry | year=2019 | journal=Science Advances | page=eaav7610 | last1 = Sala | first1 = S. | last2 = Ariga | first2 = A. | last3 = Ereditato | first3 = A. | last4 = Ferragut | first4 = R. | last5 = Giammarchi | first5 = M. | last6 = Leone | first6 = M. | last7 = Pistillo | first7 = C. | last8 = Scampoli | first8 = P. | issue=5 | pmid = 31058223 | pmc = 6499593 | bibcode = 2019SciA....5.7610S}}</ref> | |||
| ==Variations of the experiment== | ==Variations of the experiment== | ||
| ===Interference |
===Interference from individual particles=== | ||
| An important version of this experiment involves single particle detection. Illuminating the double-slit with a low intensity results in single particles being detected as white dots on the screen. Remarkably, however, an interference pattern emerges when these particles are allowed to build up one by one (see the image below). | |||
| ] | |||
| {{multiple image | |||
| | align = center | |||
| | perrow = 1 | |||
| | total_width = 320 | |||
| | image_style = border:none; | |||
| | image1 = Roger Bach et al 2013 New J. Phys. 15 033018 Figure 3 cropped to top frame.jpg | |||
| | alt1 = Electron diffraction pattern | |||
| | image2 = Electron_buildup_movie_from_"Controlled_double-slit_electron_diffraction"_Roger_Bach_et_al_2013_New_J._Phys._15_033018.gif | |||
| | alt2 = Dots slowly filling an interference pattern. | |||
| | caption2 = Experimental electron double slit diffraction pattern.<ref name="Bach Pope Liou Batelaan 2013 p=033018">{{cite journal | last1=Bach | first1=Roger | last2=Pope | first2=Damian | last3=Liou | first3=Sy-Hwang | last4=Batelaan | first4=Herman | title=Controlled double-slit electron diffraction | journal=New Journal of Physics | publisher=IOP Publishing | volume=15 | issue=3 | date=2013-03-13 | issn=1367-2630 | doi=10.1088/1367-2630/15/3/033018 | page=033018 | arxiv=1210.6243 | bibcode=2013NJPh...15c3018B | s2cid=832961 | url=https://iopscience.iop.org/article/10.1088/1367-2630/15/3/033018}}</ref> Across the middle of the image at the top, the intensity alternates from high to low, showing interference in the signal from the two slits. Bottom: movie of the pattern being built up dot-by-dot. '''Click on the thumbnail to enlarge the movie.''' | |||
| }} | |||
| This demonstrates the ], which states that all matter exhibits both wave and particle properties: The particle is measured as a single pulse at a single position, while the modulus squared of the wave describes the ] of detecting the particle at a specific place on the screen giving a statistical interference pattern.<ref>{{cite book |title=The Fabric of the Cosmos: Space, Time, and the Texture of Reality |first1=Brian |last1=Greene |publisher= Random House LLC |year=2007 |isbn=978-0-307-42853-0 |page=90 |url=https://books.google.com/books?id=DNd2K6mxLpIC&pg=PA90}}</ref> This phenomenon has been shown to occur with photons,<ref name="Ananthaswamy">{{cite book | |||
| | last1 = Ananthaswamy | |||
| | first1 = Anil | |||
| | title = Through Two Doors at Once: The Elegant Experiment That Captures the Enigma of Our Quantum Reality | |||
| | publisher = Penguin | |||
| | date = 2018 | |||
| | page = 63 | |||
| | isbn = 978-1-101-98611-0 | |||
| }}</ref> electrons,<ref>{{cite journal |last1= Donati |first1= O | last2= Missiroli |first2= G F |last3= Pozzi |first3= G |year= 1973 |title= An Experiment on Electron Interference |journal= American Journal of Physics |volume= 41 |issue = 5| pages = 639–644 |doi= 10.1119/1.1987321 |bibcode= 1973AmJPh..41..639D }}</ref> atoms, and even some molecules: with ] ({{chem|C|60}}) in 2001,<ref name="buckyballs" /><ref> {{webarchive |url= https://web.archive.org/web/20120331115055/http://www.quantum.at/research/molecule-interferometry-foundations/wave-particle-duality-of-c60.html |date= 31 March 2012 }}</ref><ref>{{cite journal |last1= Nairz | first1= Olaf |last2= Brezger |first2 = Björn |last3= Arndt |first3= Markus |first4= Anton |last4=Zeilinger |year= 2001 | title= Diffraction of Complex Molecules by Structures Made of Light |journal= Phys. Rev. Lett. |volume = 87 |issue= 16|page= 160401 | doi=10.1103/physrevlett.87.160401|arxiv = quant-ph/0110012 |bibcode = 2001PhRvL..87p0401N | pmid=11690188| s2cid= 21547361 }}</ref><ref>{{cite journal | last1 = Nairz | first1 = O | last2 = Arndt | first2 = M | last3 = Zeilinger | first3 = A | year = 2003 | title = Quantum interference experiments with large molecules | url = https://vcq.quantum.at/fileadmin/Publications/2003-17.pdf | journal = American Journal of Physics | volume = 71 | issue = 4 | pages = 319–325 | doi = 10.1119/1.1531580 | bibcode = 2003AmJPh..71..319N | access-date = 4 June 2015 | archive-url =https://web.archive.org/web/20150604203129/http://vcq.quantum.at/fileadmin/Publications/2003-17.pdf| archive-date = 4 June 2015 }}</ref> with 2 molecules of 430 atoms ({{chem|C|60|(C|12|F|25|)|10}} and {{chem|C|168|H|94|F|152|O|8|N|4|S|4}}) in 2011,<ref>{{cite journal|display-authors=etal |last1=Stefan Gerlich |title=Quantum interference of large organic molecules |journal=Nature Communications |date=5 April 2011 |volume=2 |page=263 |doi=10.1038/ncomms1263 |pmid=21468015 |pmc=3104521 |bibcode=2011NatCo...2..263G }}</ref> and with molecules of up to 2000 atoms in 2019.<ref>{{cite journal |last1=Yaakov Fein |display-authors=etal|title=Quantum superposition of molecules beyond 25kDa |journal=Nature Physics |date=Dec 2019 |volume=15|issue=12|pages=1242–1245|doi=10.1038/s41567-019-0663-9 |bibcode=2019NatPh..15.1242F|s2cid=203638258|url=https://www.nature.com/articles/s41567-019-0663-9.epdf}}</ref> | |||
| In addition to interference patterns built up from single particles, up to 4 ] photons can also show interference patterns.<ref>Hessmo, B., M. W. Mitchell, and P. Walther. CERN Courier (2004): 11.</ref> | |||
| {{anchor|Which way}} | |||
| ===Mach-Zehnder interferometer=== | |||
| {{Main|Mach–Zehnder interferometer}} | |||
| ] | |||
| The Mach–Zehnder interferometer can be seen as a simplified version of the double-slit experiment.<ref>{{Cite journal |last1=Maries |first1=Alexandru |last2=Sayer |first2=Ryan |last3=Singh |first3=Chandralekha |date=2020-07-01 |title=Can students apply the concept of "which-path" information learned in the context of Mach–Zehnder interferometer to the double-slit experiment? |url=https://pubs.aip.org/ajp/article/88/7/542/1044560/Can-students-apply-the-concept-of-which-path |journal=American Journal of Physics |language=en |volume=88 |issue=7 |pages=542–550 |doi=10.1119/10.0001357 |issn=0002-9505|arxiv=2005.07560 |bibcode=2020AmJPh..88..542M }}</ref> Instead of propagating through free space after the two slits, and hitting any position in an extended screen, in the interferometer the photons can only propagate via two paths, and hit two discrete photodetectors. This makes it possible to describe it via simple linear algebra in dimension 2, rather than differential equations. | |||
| An important version of this experiment involves single particles (or waves—for consistency, they are called particles here). Sending particles through a double-slit apparatus one at a time results in single particles appearing on the screen, as expected. Remarkably, however, an interference pattern emerges when these particles are allowed to build up one by one (see the image to the right). For example, when a laboratory apparatus was developed that could reliably fire one electron at a time through the double slit,<ref>Donati, O, Missiroli, G F, Pozzi, G (1973). An Experiment on Electron Interference. ''American Journal of Physics'' '''41''':639–644 {{doi|10.1119/1.1987321}}</ref> the emergence of an interference pattern suggested that ''each electron was interfering with itself'', and therefore in some sense the electron ''had to be going through both slits at once''<ref>Brian Greene, ''The Elegant Universe,'' p. 110</ref>—an idea that contradicts our everyday experience of discrete objects. This phenomenon has also been shown to occur with atoms and even some molecules, including ].<ref name="buckyballs" /><ref></ref><ref>Olaf Nairz, Björn Brezger, Markus Arndt, and Anton Zeilinger, Abstract, "," ''Phys. Rev. Lett.'' 87, 160401 (2001)</ref><ref>Nairz O, Arndt M, and Zeilinger A. . American Journal of Physics, 2003; 71:319–325. {{doi|10.1119/1.1531580}}</ref> So experiments with electrons add confirmatory evidence to the view of Dirac that electrons, protons, neutrons, and even larger entities that are ordinarily called particles nevertheless have their own wave nature and even their own specific frequencies. | |||
| A photon emitted by the laser hits the first beam splitter and is then in a superposition between the two possible paths. In the second beam splitter these paths interfere, causing the photon to hit the photodetector on the right with probability one, and the photodetector on the bottom with probability zero.<ref>{{Cite journal |last1=Marshman |first1=Emily |last2=Singh |first2=Chandralekha |date=2016-03-01 |title=Interactive tutorial to improve student understanding of single photon experiments involving a Mach–Zehnder interferometer |url=https://iopscience.iop.org/article/10.1088/0143-0807/37/2/024001 |journal=European Journal of Physics |volume=37 |issue=2 |pages=024001 |doi=10.1088/0143-0807/37/2/024001 |issn=0143-0807|arxiv=1602.06162 |bibcode=2016EJPh...37b4001M }}</ref> Blocking one of the paths, or equivalently detecting the presence of a photon on a path eliminates interference between the paths: both photodetectors will be hit with probability 1/2. This indicates that after the first beam splitter the photon does not take one path or another, but rather exists in a quantum superposition of the two paths.<ref name="vedral">{{cite book |first=Vlatko |last=Vedral |title=Introduction to Quantum Information Science |date=2006 |publisher=Oxford University Press |isbn=978-0-19-921570-6 |oclc=442351498 |author-link=Vlatko Vedral}}</ref> | |||
| This experimental fact is highly reproducible, and the mathematics of quantum mechanics (]) allows us to predict the exact probability of an electron striking the screen at any particular point. However, the electrons do not arrive at the screen in any predictable order. In other words, knowing where all the previous electrons appeared on the screen and in what order tells us nothing about where any future electron will hit, even though the probabilities at specific points can be calculated.<ref>Brian Greene, ''The Elegant Universe'', p. 104, pp. 109–114</ref> (Note that it is not the ''probabilities'' of photons appearing at various points along the detection screen that add or cancel, but the ''amplitudes''. Probabilities are the squares of amplitudes. Also note that if there is a cancellation of waves at some point, that does not mean that a photon disappears; it only means that the probability of a photon's appearing at that point will decrease, and the probability that it will appear somewhere else increases.) Thus, we have the appearance of a seemingly causeless selection event in a highly orderly and predictable formulation of the interference pattern. Ever since the origination of quantum mechanics, some theorists have searched for ways to incorporate additional determinants or "]" that, were they to become known, would account for the location of each individual impact with the target.<ref name="Greene_2004">{{cite book|last =Greene|first =Brian|authorlink =Brian Greene|title =] |publisher =Knopf|year =2004|pages = 204–213|isbn =0-375-41288-3}}</ref> | |||
| ==="Which-way" experiments and the principle of complementarity=== | ==="Which-way" experiments and the principle of complementarity=== | ||
| A well-known |
A well-known ] predicts that if particle detectors are positioned at the slits, showing through which slit a photon goes, the interference pattern will disappear.<ref name="Feynman" /> This which-way experiment illustrates the ] principle that photons can behave as either particles or waves, but cannot be observed as both at the same time.<ref>{{cite web | ||
| | last = Harrison | | last = Harrison | ||
| | first = David | | first = David | ||
| | coauthors = | |||
| | title = Complementarity and the Copenhagen Interpretation of Quantum Mechanics | | title = Complementarity and the Copenhagen Interpretation of Quantum Mechanics | ||
| | work = UPSCALE | | work = UPSCALE | ||
| Line 129: | Line 102: | ||
| | year = 2002 | | year = 2002 | ||
| | url = http://www.upscale.utoronto.ca/GeneralInterest/Harrison/Complementarity/CompCopen.html | | url = http://www.upscale.utoronto.ca/GeneralInterest/Harrison/Complementarity/CompCopen.html | ||
| | access-date = 21 June 2008}}</ref><ref>{{cite web | |||
| | doi = | |||
| | accessdate = 2008-06-21}}</ref><ref>{{cite web | |||
| | last = Cassidy | | last = Cassidy | ||
| | first = David | | first = David | ||
| | coauthors = | |||
| | title = Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation | | title = Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation | ||
| | work = Werner Heisenberg | | work = Werner Heisenberg | ||
| Line 139: | Line 110: | ||
| | year = 2008 | | year = 2008 | ||
| | url = http://www.aip.org/history/heisenberg/p09.htm | | url = http://www.aip.org/history/heisenberg/p09.htm | ||
| | access-date = 21 June 2008 | |||
| | doi = | |||
| | archive-date = 14 January 2016 | |||
| | accessdate = 2008-06-21}}</ref><ref>{{cite conference | |||
| | archive-url = https://web.archive.org/web/20160114094044/https://www.aip.org/history/heisenberg/p09.htm | |||
| }}</ref><ref>{{cite conference | |||
| | first = María C. | | first = María C. | ||
| | last = Boscá Díaz-Pintado | | last = Boscá Díaz-Pintado | ||
| | title = Updating the wave–particle duality | |||
| | coauthors = | |||
| | title = |
| book-title = 15th UK and European Meeting on the Foundations of Physics | ||
| | booktitle = 15th UK and European Meeting on the Foundations of Physics | |||
| | pages = | |||
| | publisher = | |||
| | date = 29–31 March 2007 | | date = 29–31 March 2007 | ||
| | location = Leeds, UK | | location = Leeds, UK | ||
| | url = http://philsci-archive.pitt.edu/archive/00003568/ | | url = http://philsci-archive.pitt.edu/archive/00003568/ | ||
| | access-date = 21 June 2008}}</ref> | |||
| | doi = | |||
| Despite the importance of this thought experiment in the history of quantum mechanics (for example, see the discussion on ]), technically feasible realizations of this experiment were not proposed until the 1970s.<ref name=Bartell1980>{{Cite journal | last1 = Bartell | first1 = L. | title = Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior | doi = 10.1103/PhysRevD.21.1698 | journal = Physical Review D | volume = 21 | issue = 6 |pages=1698–1699 | year = 1980 |bibcode = 1980PhRvD..21.1698B }}</ref> (Naive implementations of the textbook thought experiment are not possible because photons cannot be detected without absorbing the photon.) Currently, multiple experiments have been performed illustrating various aspects of complementarity.<ref name="Zeilinger1999">{{Cite journal |last1=Zeilinger |first1=A. |author-link=Anton Zeilinger |year=1999 |title=Experiment and the foundations of quantum physics |journal=Reviews of Modern Physics |volume=71 |issue=2 |pages=S288–S297 |bibcode=1999RvMPS..71..288Z |doi=10.1103/RevModPhys.71.S288}}</ref> | |||
| | accessdate = 2008-06-21}}</ref> | |||
| Despite the importance of this ''gedanken'' in the history of quantum mechanics (for example, see the discussion on ]), technically feasible realizations of this experiment were not proposed until the 1970s.<ref name=Bartell1980>{{cite doi|10.1103/PhysRevD.21.1698|noedit}}</ref> (Naive implementations of the textbook ''gedanken'' are not possible because photons cannot be detected without absorbing the photon.) Currently, multiple experiments have been performed illustrating various aspects of complementarity.<ref name=Zeilinger1999>{{cite doi|10.1103/RevModPhys.71.S288}}</ref> | |||
| An experiment performed in 1987 |
An experiment performed in 1987<ref name="Mittelstaedt">{{cite journal | ||
| | author=P. Mittelstaedt | | author=P. Mittelstaedt | ||
| | |
|author2=A. Prieur |author3=R. Schieder | ||
| | title=Unsharp particle-wave duality in a photon split-beam experiment | | title=Unsharp particle-wave duality in a photon split-beam experiment | ||
| | journal=Foundations of Physics | | journal=Foundations of Physics | ||
| | volume=17 | | volume=17 | ||
| Line 165: | Line 134: | ||
| | year=1987 | | year=1987 | ||
| | doi=10.1007/BF00734319 | | doi=10.1007/BF00734319 | ||
| |bibcode = 1987FoPh...17..891M }}</ref><ref>D.M. Greenberger and A. Yasin, "Simultaneous wave and particle knowledge in a neutron interferometer", ''Physics Letters'' '''A 128''', 391–4 (1988).</ref> produced results that demonstrated that information could be obtained regarding which path a particle had taken without destroying the interference altogether. This |
|bibcode = 1987FoPh...17..891M |s2cid=122856271 }}</ref><ref>D.M. Greenberger and A. Yasin, "Simultaneous wave and particle knowledge in a neutron interferometer", ''Physics Letters'' '''A 128''', 391–4 (1988).</ref> produced results that demonstrated that partial information could be obtained regarding which path a particle had taken without destroying the interference altogether. This "wave-particle trade-off" takes the form of an ] relating the visibility of the interference pattern and the distinguishability of the which-way paths.<ref>{{Cite journal |last=Sen |first=D. |date=2014 |title=The uncertainty relations in quantum mechanics |url=https://www.jstor.org/stable/24103129 |journal=Current Science |volume=107 |issue=2 |pages=203–218 |jstor=24103129 |issn=0011-3891 |quote="However, the 'wave-particle trade-off is now expressed in terms of an inequality, known as Englert-Greenberger duality or simply wave-particle duality relation". See also ref 24 in this work.}}</ref> | ||
| ===Delayed choice and quantum eraser variations=== | ===Delayed choice and quantum eraser variations=== | ||
| {{Main|Delayed |
{{Main|Delayed-choice quantum eraser}} | ||
| ] | |||
| ] demonstrate that extracting "which path" information ''after'' a particle passes through the slits can seem to retroactively alter its previous behavior at the slits. | |||
| ]s demonstrate that extracting "which path" information after a particle passes through the slits can seem to retroactively alter its previous behavior at the slits. | |||
| ] experiments demonstrate that wave behavior can be restored by erasing or otherwise making permanently unavailable the "which path" information. | ] experiments demonstrate that wave behavior can be restored by erasing or otherwise making permanently unavailable the "which path" information. | ||
| A simple do-it-at-home |
A simple do-it-at-home illustration of the quantum eraser phenomenon was given in an article in ''Scientific American''.<ref name="Hillmer2007">{{cite magazine|last=Hillmer|first=R.|year=2007|title=A do-it-yourself quantum eraser|url=https://www.scientificamerican.com/slideshow/a-do-it-yourself-quantum-eraser/|magazine=Scientific American|volume=296|issue=5|pages=90–95|doi=10.1038/scientificamerican0507-90|author2-link=Paul Kwiat|author2=Kwiat, P.|access-date=11 January 2016|bibcode = 2007SciAm.296e..90H }}</ref> If one sets polarizers before each slit with their axes orthogonal to each other, the interference pattern will be eliminated. The polarizers can be considered as introducing which-path information to each beam. Introducing a third polarizer in front of the detector with an axis of 45° relative to the other polarizers "erases" this information, allowing the interference pattern to reappear. This can also be accounted for by considering the light to be a classical wave,<ref name=Hillmer2007 />{{rp|91}} and also when using circular polarizers and single photons.<ref name=Chiao1995 />{{rp|6}} Implementations of the polarizers using ] photon pairs have no classical explanation.<ref name=Chiao1995>{{cite journal |last=Chiao |first=R. Y. |author2=P. G. Kwiat |author3=Steinberg, A. M. |title=Quantum non-locality in two-photon experiments at Berkeley|journal=Quantum and Semiclassical Optics: Journal of the European Optical Society Part B |year=1995 |volume=7 |issue=3 |pages=259–278 |doi=10.1088/1355-5111/7/3/006|arxiv = quant-ph/9501016 |bibcode = 1995QuSOp...7..259C |s2cid=118987962 }}</ref> | ||
| ===Weak measurement=== | ===Weak measurement=== | ||
| {{Main|Weak measurement}} | {{Main|Weak measurement}} | ||
| In a highly publicized experiment in 2012, researchers claimed to have identified the path each particle had taken without any adverse effects at all on the interference pattern generated by the particles.<ref>{{cite web|last=Francis|first=Matthew|title=Disentangling the |
In a highly publicized experiment in 2012, researchers claimed to have identified the path each particle had taken without any adverse effects at all on the interference pattern generated by the particles.<ref>{{cite web|last=Francis|first=Matthew|title=Disentangling the wave–particle duality in the double-slit experiment|url=https://arstechnica.com/science/2012/05/disentangling-the-wave-particle-duality-in-the-double-slit-experiment/|website=Ars Technica|date=21 May 2012}}</ref> In order to do this, they used a setup such that particles coming to the screen were not from a point-like source, but from a source with two intensity maxima. However, commentators such as Svensson<ref name=Svensson2013>{{cite journal|last=Svensson|first=Bengt E. Y.|title=Pedagogical Review of Quantum Measurement Theory with an Emphasis on Weak Measurements |journal=Quanta |volume=2 |issue=1 |pages=18–49 |doi=10.12743/quanta.v2i1.12 |year=2013|arxiv=1202.5148 |s2cid=119242577 }}</ref> have pointed out that there is in fact no conflict between the ]s performed in this variant of the double-slit experiment and the ]. Weak measurement followed by post-selection did not allow simultaneous position and momentum measurements for each individual particle, but rather allowed measurement of the average trajectory of the particles that arrived at different positions. In other words, the experimenters were creating a statistical map of the full trajectory landscape.<ref name=Svensson2013/> | ||
| ===Other variations=== | ===Other variations=== | ||
| ] | ] | ||
| ] | |||
| In 1967, Pfleegor and Mandel demonstrated two-source interference using two separate lasers as light sources.<ref>{{cite journal | journal=] | title=Interference of Independent Photon Beams | |
In 1967, Pfleegor and Mandel demonstrated two-source interference using two separate lasers as light sources.<ref>{{cite journal | journal=] | title=Interference of Independent Photon Beams |author1=Pfleegor, R. L. |author2=Mandel, L. | date=July 1967 | volume=159 | issue=5 | pages=1084–1088 | doi=10.1103/PhysRev.159.1084|bibcode = 1967PhRv..159.1084P }}</ref><ref>{{cite web |url=http://scienceblogs.com/principles/2010/11/interference_of_independent_ph.php |title=Interference of Independent Photon Beams: The Pfleegor-Mandel Experiment|access-date=16 June 2011 |archive-url=https://web.archive.org/web/20110103104840/http://scienceblogs.com/principles/2010/11/interference_of_independent_ph.php |archive-date=3 January 2011 }}></ref> | ||
| It was shown experimentally in 1972 that in a double-slit system where only one slit was open at any time, interference was nonetheless observed provided the path difference was such that the detected photon could have come from either slit.<ref>{{cite journal |
It was shown experimentally in 1972 that in a double-slit system where only one slit was open at any time, interference was nonetheless observed provided the path difference was such that the detected photon could have come from either slit.<ref>{{cite journal | title=An interference experiment with light beams modulated in anti-phase by an electro-optic shutter |author1=Sillitto, R.M. |author2=Wykes, Catherine | journal=Physics Letters A | year=1972 | volume=39 | issue=4 | pages=333–334 | doi=10.1016/0375-9601(72)91015-8|bibcode = 1972PhLA...39..333S }}</ref><ref>{{cite web| url = http://www.sillittopages.co.uk/80rms_35.html| title = "To a light particle"}}</ref> The experimental conditions were such that the photon density in the system was much less than 1. | ||
| In 1991, Carnal and Mlynek performed the classic Young's double slit experiment with ] helium atoms passing through micrometer-scale slits in gold foil.<ref>{{cite journal | journal=] | title=Young's Double-Slit Experiment with Atoms: A Simple Atom Interferometer |author1=Carnal, O. |author2=Mlynek, J. | date=May 1991 | volume=66 | number=21 | pages=2689–2694 | doi=10.1103/PhysRevLett.66.2689| pmid=10043591 | bibcode=1991PhRvL..66.2689C | url=http://elib.bsu.by/handle/123456789/154548 }}</ref><ref>{{cite journal |url=https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.66.2689 |title=Young's Double-Slit Experiment with Atoms: A Simple Atom Interferometer|date=1991 |doi=10.1103/PhysRevLett.66.2689 |pmid=10043591 |access-date=20 March 2022 |last1=Carnal |first1=O. |last2=Mlynek |first2=J. |journal=Physical Review Letters |volume=66 |issue=21 |pages=2689–2692 |bibcode=1991PhRvL..66.2689C }}></ref> | |||
| In 1999, a quantum interference experiment (using a diffraction grating, rather than two slits) was successfully performed with buckyball molecules (each of which comprises 60 carbon atoms).<ref name="buckyballs"> (Introduction, subscription needed for full text, quoted in full in {{Webarchive|url=https://web.archive.org/web/20170925163808/http://postbiota.org/pipermail/tt/2010-May/007336.html|date=25 September 2017}})</ref><ref>{{Cite journal |doi = 10.1038/44348|title = Wave–particle duality of C60 molecules|journal = Nature|volume = 401|issue = 6754|pages = 680–682|year = 1999|last1 = Arndt|first1 = Markus|last2 = Nairz|first2 = Olaf|last3 = Vos-Andreae|first3 = Julian|last4 = Keller|first4 = Claudia|last5 = Van Der Zouw|first5 = Gerbrand|last6 = Zeilinger|first6 = Anton|bibcode = 1999Natur.401..680A|pmid = 18494170|s2cid = 4424892}}</ref> A buckyball is large enough (diameter about 0.7 ], nearly half a million times larger than a proton) to be seen in an ]. | |||
| In 2002, an electron field emission source was used to demonstrate the double-slit experiment. In this experiment, a coherent electron wave was emitted from two closely located emission sites on the needle apex, which acted as double slits, splitting the wave into two coherent electron waves in a vacuum. The interference pattern between the two electron waves could then be observed.<ref>{{Cite journal |last1=Oshima |first1=C. |last2=Mastuda |first2=K. |last3=Kona |first3=T. |last4=Mogami |first4=Y. |last5=Komaki |first5=M. |last6=Murata |first6=Y. |last7=Yamashita |first7=T. |last8=Kuzumaki |first8=T. |last9=Horiike |first9=Y. |date=2002-01-04 |title=Young's Interference of Electrons in Field Emission Patterns |url=https://link.aps.org/doi/10.1103/PhysRevLett.88.038301 |journal=Physical Review Letters |language=en |volume=88 |issue=3 |page=038301 |doi=10.1103/PhysRevLett.88.038301 |pmid=11801091 |bibcode=2002PhRvL..88c8301O |issn=0031-9007}}</ref> In 2017, researchers performed the double-slit experiment using light-induced field electron emitters. With this technique, emission sites can be optically selected on a scale of ten nanometers. By selectively deactivating (closing) one of the two emissions (slits), researchers were able to show that the interference pattern disappeared.<ref>{{Cite journal |last1=Yanagisawa |first1=Hirofumi |last2=Ciappina |first2=Marcelo |last3=Hafner |first3=Christian |last4=Schötz |first4=Johannes |last5=Osterwalder |first5=Jürg |last6=Kling |first6=Matthias F. |date=2017-10-04 |title=Optical Control of Young's Type Double-slit Interferometer for Laser-induced Electron Emission from a Nano-tip |journal=Scientific Reports |language=en |volume=7 |issue=1 |page=12661 |doi=10.1038/s41598-017-12832-3 |issn=2045-2322 |pmc=5627254 |pmid=28978914|arxiv=1710.02216 |bibcode=2017NatSR...712661Y }}</ref> | |||
| In 2005, E. R. Eliel presented an experimental and theoretical study of the optical transmission of a thin metal screen perforated by two subwavelength slits, separated by many optical wavelengths. The total intensity of the far-field double-slit pattern is shown to be reduced or enhanced as a function of the wavelength of the incident light beam.<ref>{{cite journal|last1=Schouten|first1=H.F.|last2=Kuzmin|first2=N.|last3=Dubois|first3=G.|last4=Visser|first4=T.D.|last5=Gbur|first5=G.|last6=Alkemade|first6=P.F.A.|last7=Blok|first7=H.|last8=Hooft|first8=G.W.|last9=Lenstra|first9=D.|last10=Eliel|first10=E.R.|title=Plasmon-Assisted Two-Slit Transmission: Young's Experiment Revisited|journal=Phys. Rev. Lett.|date=7 February 2005|volume=94|issue=5|page=053901|doi=10.1103/physrevlett.94.053901|bibcode = 2005PhRvL..94e3901S|pmid=15783641|hdl=1887/71482|s2cid=19197175 |url=http://repository.tudelft.nl/islandora/object/uuid%3Abe5f0a85-ad6e-40ac-a8f3-2028a2c235c8/datastream/OBJ/view|author5-link=Greg Gbur|hdl-access=free}}<!--|access-date=7 February 2007--></ref> | |||
| In 2012, researchers at the ] performed the double-slit experiment with electrons as described by ], using new instruments that allowed control of the transmission of the two slits and the monitoring of single-electron detection events. Electrons were fired by an electron gun and passed through one or two slits of 62 nm wide × 4 μm tall.<ref>{{cite journal | In 2012, researchers at the ] performed the double-slit experiment with electrons as described by ], using new instruments that allowed control of the transmission of the two slits and the monitoring of single-electron detection events. Electrons were fired by an electron gun and passed through one or two slits of 62 nm wide × 4 μm tall.<ref>{{cite journal | ||
| | last =Bach | | last =Bach | ||
| | first =Roger | | first =Roger | ||
| | coauthors =et al. | |||
| | title =Controlled double-slit electron diffraction | | title =Controlled double-slit electron diffraction | ||
| | journal =New Journal of Physics | | journal =New Journal of Physics | ||
| | volume =15 | | volume =15 | ||
| | issue =3 | | issue =3 | ||
| | |
|page=033018 | ||
| | date =March 2013 | | date =March 2013 | ||
| | url =http://arxiv.org/abs/1210.6243 | |||
| | doi =10.1088/1367-2630/15/3/033018 | | doi =10.1088/1367-2630/15/3/033018 | ||
| |arxiv = 1210.6243 |bibcode = 2013NJPh...15c3018B | s2cid =832961 | |||
| }}</ref> | |||
| |display-authors=etal}}</ref> | |||
| In 2013, a quantum interference experiment (using diffraction gratings, rather than two slits) was successfully performed with molecules that each comprised 810 atoms (whose total mass was over 10,000 ]).<ref name="medium.com">""</ref><ref name="Eibenberger 2013 pp. 14696–14700">{{cite journal |last= Eibenberger |first=Sandra |title= Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu |journal= ] |volume=15 |issue=35 |pages= 14696–14700 |year= 2013 |doi= 10.1039/C3CP51500A |arxiv= 1310.8343 |bibcode = 2013PCCP...1514696E |display-authors=etal |pmid= 23900710|s2cid=3944699 }}</ref> The record was raised to 2000 atoms (25,000 amu) in 2019.<ref name="Yaakov Y. Fein 1242–1245"/> | |||
| In 1999, the double-slit experiment was successfully performed with ] ]s (each of which comprises 60 carbon atoms).<ref name="buckyballs"> (Introduction, subscription needed for full text, quoted in full in )</ref><ref>. Abstract, subscription needed for full text</ref> A buckyball is large enough (diameter about 0.7 ], nearly half a million times larger than a proton) to be seen under an ]. | |||
| ====Hydrodynamic pilot wave analogs==== | |||
| In 2013, the double-slit experiment was successfully performed with molecules that each comprised 810 atoms (whose total mass was over 10,000 ]).<ref name="medium.com"/><ref name="Eibenberger 2013 pp. 14696–14700"/> | |||
| ] have been developed that can recreate various aspects of quantum mechanical systems, including single-particle interference through a double-slit.<ref name=Bush2015>{{cite journal|last1=Bush|first1=John WM|title=Pilot-wave hydrodynamics|journal=Annual Review of Fluid Mechanics|date=2015|volume=47|issue=1|pages=269–292|doi=10.1146/annurev-fluid-010814-014506|url=http://math.mit.edu/~bush/wordpress/wp-content/uploads/2015/01/Bush-AnnRev2015.pdf |archive-url=https://web.archive.org/web/20150621172430/http://math.mit.edu/~bush/wordpress/wp-content/uploads/2015/01/Bush-AnnRev2015.pdf |archive-date=2015-06-21 |url-status=live|access-date=21 June 2015|bibcode = 2015AnRFM..47..269B |hdl=1721.1/89790|hdl-access=free}}</ref> A silicone oil droplet, bouncing along the surface of a liquid, self-propels via resonant interactions with its own wave field. The droplet gently sloshes the liquid with every bounce. At the same time, ripples from past bounces affect its course. The droplet's interaction with its own ripples, which form what is known as a ], causes it to exhibit behaviors previously thought to be peculiar to elementary particles – including behaviors customarily taken as evidence that elementary particles are spread through space like waves, without any specific location, until they are measured.<ref name=Bush2010>{{cite journal|last1=Bush|first1=John W. M.|title=Quantum mechanics writ large|journal=PNAS|volume=107|issue=41|pages=17455–17456|doi=10.1073/pnas.1012399107|bibcode = 2010PNAS..10717455B |pmc=2955131|year=2010|doi-access=free}}</ref><ref>{{Cite magazine |url=https://www.wired.com/2014/06/the-new-quantum-reality/ |title=Have We Been Interpreting Quantum Mechanics Wrong This Whole Time?|magazine=Wired |author=Natalie Wolchover |date=30 June 2014}}</ref> | |||
| Behaviors mimicked via this hydrodynamic pilot-wave system include quantum single particle diffraction,<ref name=CouderFort2012>{{cite journal|last1=Couder|first1=Y.|last2=Fort|first2=E.|title=Probabilities and trajectories in a classical wave–particle duality|journal=Journal of Physics: Conference Series|date=2012|volume=361|issue=1|page=012001|doi=10.1088/1742-6596/361/1/012001|bibcode = 2012JPhCS.361a2001C |doi-access=free}}</ref> tunneling, quantized orbits, orbital level splitting, spin, and multimodal statistics. It is also possible to infer uncertainty relations and exclusion principles. Videos are available illustrating various features of this system. ] | |||
| However, more complicated systems that involve two or more particles in superposition are not amenable to such a simple, classically intuitive explanation.<ref name="Baggott, Jim 2011 pp. 76">Baggott, Jim (2011). ''The Quantum Story: A History in 40 Moments''. New York: Oxford University Press. pp. 76. ("The wavefunction of a system containing ''N'' particles depends on 3''N'' position coordinates and is a function in a 3''N''-dimensional configuration space or 'phase space'. It is difficult to visualize a reality comprising imaginary functions in an abstract, multi-dimensional space. No difficulty arises, however, if the imaginary functions are not to be given a real interpretation.")</ref> Accordingly, no hydrodynamic analog of entanglement has been developed.<ref name=Bush2015/> Nevertheless, optical analogs are possible.<ref>{{Cite journal | doi=10.1038/srep18574| pmid=26689679| pmc=4686973| title=Classical hypercorrelation and wave-optics analogy of quantum superdense coding| journal=Scientific Reports| volume=5| page=18574| year=2016| last1=Li| first1=Pengyun| last2=Sun| first2=Yifan| last3=Yang| first3=Zhenwei| last4=Song| first4=Xinbing| last5=Zhang| first5=Xiangdong| bibcode=2015NatSR...518574L}}</ref> | |||
| ==== Double-slit experiment on time ==== | |||
| In 2023, an experiment was reported recreating an interference pattern in time by shining a ] pulse at a screen coated in ] which would alter the properties of the electrons within the material due to the ], changing it from transparent to reflective for around 200 femtoseconds long where a subsequent probe laser beam hitting the ITO screen would then see this temporary change in optical properties as a slit in time and two of them as a double slit with a phase difference adding up destructively or constructively on each frequency component resulting in an interference pattern.<ref name=":0">{{Cite journal |last1=Bacot |first1=Vincent |last2=Labousse |first2=Matthieu |last3=Eddi |first3=Antonin |last4=Fink |first4=Mathias |last5=Fort |first5=Emmanuel |date=November 2016 |title=Time reversal and holography with spacetime transformations |url=https://www.nature.com/articles/nphys3810 |journal=Nature Physics |language=en |volume=12 |issue=10 |pages=972–977 |doi=10.1038/nphys3810 |arxiv=1510.01277 |bibcode=2016NatPh..12..972B |s2cid=53536274 |issn=1745-2481}}</ref><ref>{{Cite journal |last=Rodríguez-Fortuño |first=Francisco J. |date=2023-04-03 |title=An optical double-slit experiment in time |url=https://www.nature.com/articles/s41567-023-02026-2 |journal=Nature Physics |volume=19 |issue=7 |language=en |pages=929–930 |doi=10.1038/s41567-023-02026-2 |bibcode=2023NatPh..19..929R |s2cid=257945438 |issn=1745-2481}}</ref><ref name=":1">{{Cite journal |last=Castelvecchi |first=Davide |date=2023-04-03 |title=Light waves squeezed through 'slits in time' |url=https://www.nature.com/articles/d41586-023-00968-4 |journal=Nature |language=en |volume=616 |issue=7956 |page=230 |doi=10.1038/d41586-023-00968-4|pmid=37012471 |bibcode=2023Natur.616..230C |s2cid=257922697 }}</ref> Similar results have been obtained classically on water waves.<ref name=":0" /><ref name=":1" /> | |||
| ==Classical wave-optics formulation== | ==Classical wave-optics formulation== | ||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| Much of the behaviour of light can be modelled using classical wave theory. The ] is one such model; it states that each point on a wavefront generates a secondary |
Much of the behaviour of light can be modelled using classical wave theory. The ] is one such model; it states that each point on a wavefront generates a secondary wavelet, and that the disturbance at any subsequent point can be found by ] the contributions of the individual wavelets at that point. This summation needs to take into account the ] as well as the ] of the individual wavelets. Only the ] of a light field can be measured—this is proportional to the square of the amplitude. | ||
| In the double-slit experiment, the two slits are illuminated by a single laser |
In the double-slit experiment, the two slits are illuminated by the quasi-monochromatic light of a single laser. If the width of the slits is small enough (much less than the wavelength of the laser light), the slits diffract the light into cylindrical waves. These two cylindrical wavefronts are superimposed, and the amplitude, and therefore the intensity, at any point in the combined wavefronts depends on both the magnitude and the phase of the two wavefronts. The difference in phase between the two waves is determined by the difference in the distance travelled by the two waves. | ||
| If the viewing distance is large compared with the separation of the slits (the ]), the phase difference can be found using the geometry shown in the figure below right. The path difference between two waves travelling at an angle {{math|θ}} is given by: | If the viewing distance is large compared with the separation of the slits (the ]), the phase difference can be found using the geometry shown in the figure below right. The path difference between two waves travelling at an angle {{math|θ}} is given by: | ||
| Line 216: | Line 204: | ||
| :<math>d \sin \theta \approx d \theta</math> | :<math>d \sin \theta \approx d \theta</math> | ||
| When the two waves are in phase, i.e. the path difference is equal to an integral number of wavelengths, the summed amplitude, and therefore the summed intensity is maximum, and when they are in anti-phase, i.e. the path difference is equal to half a wavelength, one and a half wavelengths, etc., then the two waves cancel and the summed intensity is zero. This effect is known as ]. The interference fringe maxima occur at angles | Where d is the distance between the two slits. When the two waves are in phase, i.e. the path difference is equal to an integral number of wavelengths, the summed amplitude, and therefore the summed intensity is maximum, and when they are in anti-phase, i.e. the path difference is equal to half a wavelength, one and a half wavelengths, etc., then the two waves cancel and the summed intensity is zero. This effect is known as ]. The interference fringe maxima occur at angles | ||
| :<math>~ d \theta_n = n \lambda,~ n=0,1,2,\ldots</math> | :<math>~ d \theta_n = n \lambda,~ n=0,1,2,\ldots</math> | ||
| Line 228: | Line 216: | ||
| :<math>~w=z \theta_f = z \lambda /d</math> | :<math>~w=z \theta_f = z \lambda /d</math> | ||
| For example, if two slits are separated by 0. |
For example, if two slits are separated by 0.5 mm ({{math|''d''}}), and are illuminated with a 0.6 μm wavelength laser ({{math|λ}}), then at a distance of 1 m ({{math|''z''}}), the spacing of the fringes will be 1.2 mm. | ||
| If the width of the slits {{math|''b''}} is |
If the width of the slits {{math|''b''}} is appreciable compared to the wavelength, the ] equation is needed to determine the intensity of the diffracted light as follows:<ref>Jenkins FA and White HE, Fundamentals of Optics, 1967, McGraw Hill, New York</ref> | ||
| :<math> | :<math> | ||
| Line 239: | Line 227: | ||
| </math> | </math> | ||
| where the ] is defined as sinc(''x'') = sin(''x'')/''x'' for ''x'' ≠ 0, and sinc(0) = 1. | |||
| This is illustrated in the figure above, where the first pattern is the diffraction pattern of a single slit, given by the {{math|sinc}} function in this equation, and the second figure shows the combined intensity of the light diffracted from the two slits, where the {{math|cos}} function |
This is illustrated in the figure above, where the first pattern is the diffraction pattern of a single slit, given by the {{math|sinc}} function in this equation, and the second figure shows the combined intensity of the light diffracted from the two slits, where the {{math|cos}} function represents the fine structure, and the coarser structure represents diffraction by the individual slits as described by the {{math|sinc}} function. | ||
| Similar calculations for the ] can be |
Similar calculations for the ] can be made by applying the ] equation, which implies that as the plane of observation gets closer to the plane in which the slits are located, the diffraction patterns associated with each slit decrease in size, so that the area in which interference occurs is reduced, and may vanish altogether when there is no overlap in the two diffracted patterns.<ref>Longhurst RS, Physical and Geometrical Optics, 1967, 2nd Edition, Longmans</ref> | ||
| ==Path-integral formulation== | |||
| ==Interpretations of the experiment== | |||
| ])]] | |||
| Like the ] thought experiment, the double-slit experiment is often used to highlight the differences and similarities between the various ]. | |||
| The double-slit experiment can illustrate the ] of quantum mechanics provided by Feynman.<ref>{{cite book|last=Zee |first=Anthony |title=Quantum Field Theory in a Nutshell |author-link=Anthony Zee |title-link=Quantum Field Theory in a Nutshell |publisher=Princeton University Press |edition=2nd |year=2010 |isbn=978-0-691-14034-6 |pages=2–16}}</ref> The path integral formulation replaces the classical notion of a single, unique trajectory for a system, with a sum over all possible trajectories. The trajectories are added together by using ]. | |||
| ===Copenhagen interpretation=== | |||
| {{unreferenced section|date=February 2012}} | |||
| The ] is a consensus among some of the pioneers in the field of quantum mechanics that it is undesirable to posit anything that goes beyond the mathematical formulae and the kinds of physical apparatus and reactions that enable us to gain some knowledge of what goes on at the atomic scale. One of the mathematical constructs that enables experimenters to predict very accurately certain experimental results is sometimes called a probability wave. In its mathematical form it is analogous to the description of a physical wave, but its "crests" and "troughs" indicate levels of probability for the occurrence of certain phenomena (e.g., a spark of light at a certain point on a detector screen) that can be observed in the macro world of ordinary human experience. | |||
| The probability "wave" can be said to "pass through space" because the probability values that one can compute from its mathematical representation are dependent on time. One cannot speak of the location of any particle such as a photon between the time it is emitted and the time it is detected simply because in order to say that something is located somewhere at a certain time one has to detect it. The requirement for the eventual appearance of an interference pattern is that particles be emitted, and that there be a screen with at least two distinct paths for the particle to take from the emitter to the detection screen. Experiments observe nothing whatsoever between the time of emission of the particle and its arrival at the detection screen. If a ray tracing is then made as if a light wave (as understood in classical physics) is wide enough to take both paths, then that ray tracing will accurately predict the appearance of maxima and minima on the detector screen when many particles pass through the apparatus and gradually "paint" the expected interference pattern. | |||
| ===Path-integral formulation=== | |||
| ].)]] | |||
| The Copenhagen interpretation is similar to the ] of quantum mechanics provided by Feynman. The path integral formulation replaces the classical notion of a single, unique trajectory for a system, with a sum over all possible trajectories. The trajectories are added together by using ]. | |||
| Each path is considered equally likely, and thus contributes the same amount. However, the ] of this contribution at any given point along the path is determined by the ] along the path: | Each path is considered equally likely, and thus contributes the same amount. However, the ] of this contribution at any given point along the path is determined by the ] along the path: | ||
| <math display="block">A_{\text{path}}(x,y,z,t) = e^{i S(x,y,z,t)}</math> | |||
| ::<math>A_{\text{path}}(x,y,z,t) = e^{i S(x,y,z,t)}</math> | |||
| All these contributions are then added together, and the ] of the final result is ], to get the probability distribution for the position of a particle: | All these contributions are then added together, and the ] of the final result is ], to get the probability distribution for the position of a particle: | ||
| <math display="block">p(x,y,z,t) \propto \left\vert \int_{\text{all paths}} e^{i S(x,y,z,t)} \right\vert ^2 </math> | |||
| ::<math>p(x,y,z,t) \propto \left\vert \int_{\text{all paths}} e^{i S(x,y,z,t)} \right\vert ^2 </math> | |||
| As is always the case when calculating ], the results must then be ] by imposing: | As is always the case when calculating ], the results must then be ] by imposing: | ||
| <math display="block">\iiint_{\text{all space}}p(x,y,z,t)\,dV = 1</math> | |||
| The probability distribution of the outcome is the normalized square of the norm of the ], over all paths from the point of origin to the final point, of ]s ] ] to the action along each path. The differences in the cumulative action along the different paths (and thus the relative phases of the contributions) produces the ] observed by the double-slit experiment. Feynman stressed that his formulation is merely a mathematical description, not an attempt to describe a real process that we can measure. | |||
| ::<math>\iiint_{\text{all space}}p(x,y,z,t)\,\mathrm{d}V = 1</math> | |||
| ==Interpretations of the experiment== | |||
| To summarize, the probability distribution of the outcome is the normalized square of the norm of the ], over all paths from the point of origin to the final point, of ]s ] ] to the action along each path. The differences in the cumulative action along the different paths (and thus the relative phases of the contributions) produces the ] observed by the double-slit experiment. Feynman stressed that his formulation is merely a mathematical description, not an attempt to describe a real process that we can measure. | |||
| Like the ] ], the double-slit experiment is often used to highlight the differences and similarities between the various ]. | |||
| === |
===Standard quantum physics=== | ||
| The standard interpretation of the double slit experiment is that the pattern is a wave phenomenon, representing interference between two probability amplitudes, one for each slit. Low intensity experiments demonstrate that the pattern is filled in one particle detection at a time. Any change to the apparatus designed to detect a particle at a particular slit alters the probability amplitudes and the interference disappears.<ref name="Zeilinger1999" />{{rp|S298}} This interpretation is independent of any conscious observer.<ref>{{Cite journal |last=Mandel |first=L. |date=1999-03-01 |title=Quantum effects in one-photon and two-photon interference |url=https://link.aps.org/doi/10.1103/RevModPhys.71.S274 |journal=Reviews of Modern Physics |language=en |volume=71 |issue=2 |pages=S274–S282 |doi=10.1103/RevModPhys.71.S274 |bibcode=1999RvMPS..71..274M |issn=0034-6861}}</ref>{{rp|S281|q= | |||
| According to the ], first proposed by ],<ref>{{Cite journal|doi = 10.1007/BF02302261|last = Rovelli|first = Carlo|authorlink = Carlo Rovelli|title = Relational Quantum Mechanics|journal = International Journal of Theoretical Physics|volume = 35|issue = 8|pages = 1637–1678|year = 1996|arxiv = quant-ph/9609002 |bibcode = 1996IJTP...35.1637R }}</ref> observations such as those in the double-slit experiment result specifically from the interaction between the ] (measuring device) and the object being observed (physically interacted with), not any absolute property possessed by the object. In the case of an electron, if it is initially "observed" at a particular slit, then the observer–particle (photon–electron) interaction includes information about the electron's position. This partially constrains the particle's eventual location at the screen. If it is "observed" (measured with a photon) not at a particular slit but rather at the screen, then there is no "which path" information as part of the interaction, so the electron's "observed" position on the screen is determined strictly by its probability function. This makes the resulting pattern on the screen the same as if each individual electron had passed through both slits. It has also been suggested that space and distance themselves are relational, and that an electron can appear to be in "two places at once"—for example, at both slits—because its spatial relations to particular points on the screen remain identical from both slit locations.<ref>{{Cite journal|last = Filk|first = Thomas|title = Relational Interpretation of the Wave Function and a Possible Way Around Bell’s Theorem|journal = International Journal of Theoretical Physics|volume = 45|pages = 1205–1219|year = 2006|url = http://www.springerlink.com/content/v775765467462313/|doi = 10.1007/s10773-006-9125-0|arxiv = quant-ph/0602060 |bibcode = 2006IJTP...45.1166F }}</ref> | |||
| The analysis of some interference experiments confronts us with fundamental questions of interpretation and brings out that the quantum state reflects not what we know about the system, but rather what is knowable in principle. This avoids any reference to consciousness in the interpretation of the state.}} | |||
| ===Complementarity=== | |||
| ===de Broglie's wave mechanics=== | |||
| {{main|Complementarity (physics)}} | |||
| ] interpreted quantum experiments like the double-slit experiment using the concept of complementarity.<ref name="Faye-Stanford">{{Cite book|last=Faye|first=Jan|title=]|publisher=Metaphysics Research Lab, Stanford University|year=2019|editor-last=Zalta|editor-first=Edward N.|chapter=Copenhagen Interpretation of Quantum Mechanics|author-link=Jan Faye|chapter-url=https://plato.stanford.edu/entries/qm-copenhagen/}}</ref> In Bohr's view quantum systems are not classical, but measurements can only give classical results. Certain pairs of classical properties will never be observed in a quantum system simultaneously: the interference pattern of waves in the double slit experiment will disappear if particles are detected at the slits. Modern quantitative versions of the concept allow for a continuous tradeoff between the visibility of the interference fringes and the probability of particle detection at a slit.<ref>{{Cite journal |last1=Wootters |first1=William K. |last2=Zurek |first2=Wojciech H. |date=1979-01-15 |title=Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr's principle |url=https://link.aps.org/doi/10.1103/PhysRevD.19.473 |journal=Physical Review D |language=en |volume=19 |issue=2 |pages=473–484 |doi=10.1103/PhysRevD.19.473 |bibcode=1979PhRvD..19..473W |issn=0556-2821}}</ref><ref>{{Cite journal |last=Bartell |first=L. S. |date=1980-03-15 |title=Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior |url=https://link.aps.org/doi/10.1103/PhysRevD.21.1698 |journal=Physical Review D |language=en |volume=21 |issue=6 |pages=1698–1699 |doi=10.1103/PhysRevD.21.1698 |bibcode=1980PhRvD..21.1698B |issn=0556-2821}}</ref> | |||
| ===Copenhagen interpretation=== | |||
| {{quote | When in 1923–1924 I had my first ideas about Wave Mechanics I was looking for a truly concrete physical image, valid for all particles, of the wave and particle coexistence discovered by Albert Einstein in his "Theory of light quanta". I had no doubt whatsoever about the physical reality of waves and particles.<br> | |||
| {{Main|Copenhagen interpretation}} | |||
| The ] is a collection of views about the meaning of ], stemming from the work of ], ], ], and others. The term "Copenhagen interpretation" was apparently coined by Heisenberg during the 1950s to refer to ideas developed in the 1925–1927 period, glossing over his disagreements with Bohr.<ref name="Faye-Stanford"/><ref name="camilleri2015">{{cite journal|first1=K. |last1=Camilleri |first2=M. |last2=Schlosshauer |title=Niels Bohr as Philosopher of Experiment: Does Decoherence Theory Challenge Bohr's Doctrine of Classical Concepts? |arxiv=1502.06547 |journal=] |volume=49 |pages=73–83 |year=2015 |doi=10.1016/j.shpsb.2015.01.005|bibcode=2015SHPMP..49...73C |s2cid=27697360 }}</ref><ref>{{cite book |last=Scheibe |first=Erhard |title=The Logical Analysis of Quantum Mechanics |publisher=Pergamon Press |year=1973 |isbn=978-0-08-017158-6 |oclc=799397091 |quote=here is no point in looking for ''the'' Copenhagen interpretation as a unified and consistent logical structure. Terms such as "Copenhagen interpretation" or "Copenhagen school" are based on the history of the development of quantum mechanics; they form a simplified and often convenient way of referring to the ideas of a number of physicists who played an important role in the establishment of quantum mechanics, and who were collaborators of Bohr's at his Institute or took part in the discussions during the crucial years. On closer inspection, one sees quite easily that these ideas are divergent in detail and that in particular the views of Bohr, the spiritual leader of the school, form a separate entity which can now be understood only by a thorough study of as many as possible of the relevant publications by Bohr himself. |author-link=Erhard Scheibe}}</ref><ref name="Mermin 2017">{{Cite book |last=Mermin |first=N. David |title=Quantum Speakables II |date=2017-01-01 |publisher=Springer International Publishing |isbn=978-3-319-38985-1 |editor-last=Bertlmann |editor-first=Reinhold |series=The Frontiers Collection |pages=83–93 |language=en |chapter=Why QBism Is Not the Copenhagen Interpretation and What John Bell Might Have Thought of It |doi=10.1007/978-3-319-38987-5_4 |editor2-last=Zeilinger |editor2-first=Anton |editor-link2=Anton Zeilinger |arxiv=1409.2454 |s2cid=118458259}}</ref> Consequently, there is no definitive historical statement of what the interpretation entails. Features common across versions of the Copenhagen interpretation include the idea that quantum mechanics is intrinsically ], with probabilities calculated using the ], and some form of ] principle.<ref name="omnes1999">{{cite book|last=Omnès |first=Roland |author-link=Roland Omnès |chapter=The Copenhagen Interpretation |title=Understanding Quantum Mechanics |publisher=Princeton University Press |year=1999 |doi=10.2307/j.ctv173f2pm.9 |s2cid=203390914 }}</ref>{{rp|41–54}} Moreover, the act of "observing" or "measuring" an object is irreversible, and no truth can be attributed to an object, ]. In the Copenhagen interpretation, complementarity means a particular experiment can demonstrate particle behavior (passing through a definite slit) or wave behavior (interference), but not both at the same time.<ref name="omnes1999"/>{{rp|49|q=We may speak of an electron by using the language of waves when it crosses two slits in an interfering device, and we speak of the same electron as a particle when it is detected, but we cannot use the two modes of speaking at the same time.}}<ref>{{Cite journal |last=Rosenfeld |first=L. |author-link=Léon Rosenfeld |date=1953 |title=Strife about Complementarity |journal=Science Progress (1933– ) |volume=41 |issue=163 |pages=393–410 |issn=0036-8504 |jstor=43414997}}</ref><ref name="peres">{{Cite book|last=Peres|first=Asher|title=]|publisher=Kluwer Academic Publishers|year=1995|isbn=0-7923-2549-4|author-link=Asher Peres |pages=36–39}}</ref> In a Copenhagen-type view, the question of which slit a particle travels through has no meaning when there is no detector.<ref name="omnes">{{cite book|first=R. |last=Omnès |author-link=Roland Omnès |title=The Interpretation of Quantum Mechanics |publisher=Princeton University Press |year=1994 |isbn=978-0-691-03669-4 |oclc=439453957 |page=167}}</ref><ref>{{cite book |last1=Brukner |first1=Časlav |chapter=Quantum Physics as a Science of Information |date=2005 |title=Quo Vadis Quantum Mechanics? |pages=47–61 |editor-last=Elitzur |editor-first=Avshalom C. |place=Berlin, Heidelberg |publisher=Springer |language=en |doi=10.1007/3-540-26669-0_3 |isbn=978-3-540-22188-3 |last2=Zeilinger |first2=Anton |author-link1=Časlav Brukner |author-link2=Anton Zeilinger |editor2-last=Dolev |editor2-first=Shahar |editor3-last=Kolenda |editor3-first=Nancy}}</ref> | |||
| ===Relational interpretation=== | |||
| For me, the particle, precisely located in space at every instant, forms on the ''v'' wave a small region of high energy concentration, which may be likened in a first approximation, to a moving singularity.<ref name=deBroglie>{{cite journal |last=de Broglie |first=Louis |title=Interpretation of quantum mechanics by the double solution theory |url=http://aflb.ensmp.fr/AFLB-classiques/aflb124p001.pdf}}</ref> —]}} | |||
| According to the ], first proposed by ],<ref>{{Cite journal|doi = 10.1007/BF02302261|last = Rovelli|first = Carlo|author-link = Carlo Rovelli|title = Relational Quantum Mechanics|journal = International Journal of Theoretical Physics|volume = 35|issue = 8|pages = 1637–1678|year = 1996|arxiv = quant-ph/9609002 |bibcode = 1996IJTP...35.1637R |s2cid = 16325959}}</ref> observations such as those in the double-slit experiment result specifically from the interaction between the ] (measuring device) and the object being observed (physically interacted with), not any absolute property possessed by the object. In the case of an electron, if it is initially "observed" at a particular slit, then the observer–particle (photon–electron) interaction includes information about the electron's position. This partially constrains the particle's eventual location at the screen. If it is "observed" (measured with a photon) not at a particular slit but rather at the screen, then there is no "which path" information as part of the interaction, so the electron's "observed" position on the screen is determined strictly by its probability function. This makes the resulting pattern on the screen the same as if each individual electron had passed through both slits.{{citation needed|date=September 2023}} | |||
| De Broglie's idea for interpreting particle–wave duality was that a particle is a moving singularity with an associated wave. | |||
| {{quote | Any particle, even isolated, has to be imagined as in continuous 'energetic contact' with a hidden medium<ref>L. de Broglie, p. 22.</ref>}} | |||
| In this interpretation, it is the hidden medium which waves. The "energetic contact" can be assumed to be the particle moving through and displacing the hidden medium, analogous to the ] of a boat. The hidden medium is analogous to a ] as the particle does not slow down and what ] describes as a piece of window glass, "Subsequent studies with large particle accelerators have now led us to understand that space is more like a piece of window glass than ideal Newtonian emptiness."<ref>Robert B. Laughlin, "]"</ref> | |||
| In a double slit experiment the particle travels a well defined path that takes it through one slit. The associated wave in the hidden medium passes through both. As the wave exits the slits it creates ]. As the particle exits a single slit the direction it travels is altered by the wave interference. This is the wave piloting the particle. Detecting the particle strongly exiting a single slit destroys the cohesion between the particle and its associated wave and the particle continues on the trajectory it was traveling. | |||
| Aephraim Steinberg's experiments on measuring both average position and momentum of photons were described in terms of the ] theory, in several reviews: | |||
| {{quote | Intriguingly, the trajectories closely match those predicted by an unconventional interpretation of quantum mechanics known as pilot-wave theory, in which each particle has a well-defined trajectory that takes it through one slit while the associated wave passes through both slits.<ref>{{cite journal |last=Cartlidge |first=Edwin |title=New 'Double Slit' Experiment Skirts Uncertainty Principle |url=http://www.scientificamerican.com/article.cfm?id=new-double-slit-experiment-skirts-uncertainty-principle}}</ref>}} | |||
| ===Many-worlds interpretation=== | |||
| {{quote | For his part, Professor Steinberg believes that the result reduces a limitation not on quantum physics but on physicists themselves. "I feel like we're starting to pull back a veil on what nature really is," he said. "The trouble with quantum mechanics is that while we've learned to calculate the outcomes of all sorts of experiments, we've lost much of our ability to describe what is really happening in any natural language. I think that this has really hampered our ability to make progress, to come up with new ideas and see intuitively how new systems ought to behave."<ref name=Steinberg2>{{cite journal |last=Palmer |first=Jason |title=Team 'sneaks around' quantum rule |url=http://www.bbc.co.uk/news/science-environment-13626587}}</ref>}} | |||
| As with Copenhagen, there are multiple variants of the ]. The unifying theme is that physical reality is identified with a wavefunction, and this wavefunction always evolves unitarily, i.e., following the Schrödinger equation with no collapses.<ref>{{Cite journal|last=Kent|first=Adrian|author-link=Adrian Kent|date=February 2015|title=Does it Make Sense to Speak of Self-Locating Uncertainty in the Universal Wave Function? Remarks on Sebens and Carroll |journal=Foundations of Physics |language=en |volume=45 |issue=2 |pages=211–217 |arxiv=1408.1944 |doi=10.1007/s10701-014-9862-5 |issn=0015-9018 |bibcode=2015FoPh...45..211K |s2cid=118471198}}</ref><ref name="vaidman_stanfordencyclopedia">{{cite SEP |last=Vaidman |first=Lev |author-link=Lev Vaidman |title=Many-Worlds Interpretation of Quantum Mechanics |url-id=qm-manyworlds |date=5 August 2021 }}</ref> Consequently, there are many parallel universes, which only interact with each other through interference. ] argues that the way to understand the double-slit experiment is that in each universe the particle travels through a specific slit, but its motion is affected by interference with particles in other universes, and this interference creates the observable fringes.<ref>{{Cite book |last=Deutsch |first=David |url=http://archive.org/details/fabricofreality0000deut |title=The Fabric of Reality |date=1998 |location=London |publisher=Penguin |isbn=978-0-14-014690-5|pages=40–53}}</ref> David Wallace, another advocate of the many-worlds interpretation, writes that in the familiar setup of the double-slit experiment the two paths are not sufficiently separated for a description in terms of parallel universes to make sense.<ref>{{cite book|first=David |last=Wallace |title=The Emergent Multiverse |page=382 |publisher=Oxford University Press |location=Oxford |isbn=978-0-19-954696-1 |year=2012}}</ref> | |||
| ===De Broglie–Bohm theory=== | |||
| {{quote | Steinberg's work stood out because it challenges the widely held notion that quantum mechanics forbids us any knowledge of the paths taken by individual photons as they travel through two closely spaced slits to create an interference pattern.<ref>{{cite journal ||title=Physics World reveals its top 10 breakthroughs for 2011 |url=http://physicsworld.com/cws/article/news/2011/dec/16/physics-world-reveals-its-top-10-breakthroughs-for-2011}}</ref>}} | |||
| {{Main|de Broglie–Bohm theory}} | |||
| An alternative to the standard understanding of quantum mechanics, the ] states that particles also have precise locations at all times, and that their velocities are defined by the wave-function. So while a single particle will travel through one particular slit in the double-slit experiment, the so-called "pilot wave" that influences it will travel through both. The two slit de Broglie-Bohm trajectories were first calculated by Chris Dewdney while working with Chris Philippidis and Basil Hiley at Birkbeck College (London).<ref>{{Cite journal|last1=Philippidis|first1=C.|last2=Dewdney|first2=C.|last3=Hiley|first3=B. J.|date=1979|title=Quantum interference and the quantum potential|journal=Il Nuovo Cimento B|language=en|volume=52|issue=1|pages=15–28|doi=10.1007/bf02743566|issn=1826-9877|bibcode=1979NCimB..52...15P|s2cid=53575967}}</ref> The de Broglie-Bohm theory produces the same statistical results as standard quantum mechanics, but dispenses with many of its conceptual difficulties by adding complexity through an ''ad hoc'' quantum potential to guide the particles.<ref>{{Cite book | chapter-url=https://plato.stanford.edu/entries/qm-bohm/ | title=The Stanford Encyclopedia of Philosophy| chapter=Bohmian Mechanics| publisher=Metaphysics Research Lab, Stanford University| year=2017}}</ref> | |||
| While the model is in many ways similar to ], it is known to fail for relativistic cases<ref>{{Citation |last=Goldstein |first=Sheldon |title=Bohmian Mechanics |date=2021 |url=https://plato.stanford.edu/archives/fall2021/entries/qm-bohm/ |encyclopedia=The Stanford Encyclopedia of Philosophy |editor-last=Zalta |editor-first=Edward N. |access-date=2023-08-14 |edition=Fall 2021 |publisher=Metaphysics Research Lab, Stanford University}}</ref> and does not account for features such as particle creation or annihilation in ]. Many authors such as nobel laureates ],<ref>{{Cite journal |last=Heisenberg |first=W. |date=1956 |editor-last=Pauli |editor-first=W |title=''Niels Bohr and the Development of Physics: Essays Dedicated to Niels Bohr on the Occasion of his Seventieth Birthday'' |journal=Physics Today |volume=9 |issue=8 |page=12 |doi=10.1063/1.3060063 |issn=0031-9228}}</ref> Sir ]<ref>{{Cite journal |last=Leggett |first=A J |date=2002 |title=Testing the limits of quantum mechanics: motivation, state of play, prospects |url=https://iopscience.iop.org/article/10.1088/0953-8984/14/15/201 |journal=Journal of Physics: Condensed Matter |volume=14 |issue=15 |pages=R415–R451 |doi=10.1088/0953-8984/14/15/201 |s2cid=250911999 |issn=0953-8984}}</ref> and Sir ]<ref>{{Cite book |last=Penrose |first=Roger |title=The Road to Reality: A Complete Guide to the Laws of the Universe |year=2004 |publisher=Cape |isbn=978-0-224-04447-9 |url=https://books.google.com/books?id=SkwiEAAAQBAJ |location=London}}</ref> have criticized it for not adding anything new. | |||
| Walking droplets | |||
| More complex variants of this type of approach have appeared, for instance the ''three wave hypothesis''<ref>{{Cite journal |last=Horodecki |first=R. |date=1981 |title=De broglie wave and its dual wave |journal=Physics Letters A |volume=87 |issue=3 |pages=95–97 |doi=10.1016/0375-9601(81)90571-5 |bibcode=1981PhLA...87...95H |issn=0375-9601}}</ref><ref>{{Cite journal |last=Horodecki |first=R. |date=1983 |title=Superluminal singular dual wave |journal=Lettere al Nuovo Cimento |volume=36 |issue=15 |pages=509–511 |doi=10.1007/bf02817964 |s2cid=120784358 |issn=1827-613X}}</ref> of ] as well as other complicated combinations of de Broglie and Compton waves.<ref>{{Cite journal |last=Das |first=S.N. |date=1984 |title=De Broglie wave and Compton wave |journal=Physics Letters A |volume=102 |issue=8 |pages=338–339 |doi=10.1016/0375-9601(84)90291-3 |bibcode=1984PhLA..102..338D |issn=0375-9601}}</ref><ref>{{Cite journal |last=Mukhopadhyay |first=P. |date=1986 |title=A correlation between the compton wavelength and the de Broglie wavelength |journal=Physics Letters A |volume=114 |issue=4 |pages=179–182 |doi=10.1016/0375-9601(86)90200-8 |bibcode=1986PhLA..114..179M |issn=0375-9601}}</ref><ref>{{Cite journal |last=Elbaz |first=Claude |date=1985 |title=On de Broglie waves and Compton waves of massive particles |journal=Physics Letters A |volume=109 |issue=1–2 |pages=7–8 |doi=10.1016/0375-9601(85)90379-2 |bibcode=1985PhLA..109....7E |issn=0375-9601}}</ref> To date there is no evidence that these are useful. | |||
| {{quote | Yves Couder and co-workers recently discovered a macroscopic pilot wave system in the form of ''walking droplets''. This system exhibits behaviour of a pilot wave, heretofore considered to be reserved to microscopic phenomena.<ref>Y. Couder, A. Boudaoud, S. Protière, Julien Moukhtar, E. Fort: ''Walking droplets: a form of wave-particle duality at macroscopic level?'' , {{doi|10.1051/epn/2010101}}, ()</ref>}} | |||
| {{Multiple image | |||
| {{quote | MIT researchers expand the range of quantum behaviors that can be replicated in fluidic systems, offering a new perspective on wave-particle duality.<ref>{{cite journal |last=Hardesty |first=Larry |title=When fluid dynamics mimic quantum mechanics |url=http://newsoffice.mit.edu/2013/when-fluid-dynamics-mimic-quantum-mechanics-0729}}</ref> "Whatever the case may be in quantum mechanics, the statistics are an incomplete description of our fluid system and emerge from an underlying pilot-wave dynamics<ref>{{cite AV media |people=D. Harris, J. Bush|title=The pilot-wave dynamics of walking droplets - 2:10 mark |url=https://www.youtube.com/watch?v=nmC0ygr08tE}}</ref> This physical picture is remakably similar to an early model of quantum dynamics proposed by Louis de Broglie..."<ref>{{cite AV media |people=D. Harris, J. Bush|title=The pilot-wave dynamics of walking droplets - 2:35 mark |url=https://www.youtube.com/watch?v=nmC0ygr08tE}}</ref>}} | |||
| | image1 = Doppelspalt.svg | |||
| | caption1 = Trajectories of particles in De Broglie–Bohm theory in the double-slit experiment. | |||
| | image2 = 100 trajectories guided by the wave function.png | |||
| | caption2 = 100 trajectories guided by the wave function. In De Broglie-Bohm's theory, a particle is represented, at any time, by a wave function ''and'' a position (center of mass). This is a kind of augmented reality compared to the standard interpretation. | |||
| | image3 = Interference electrons double-slit at 10cm.png | |||
| | caption3 = Numerical simulation of the double-slit experiment with electrons. Figure on the left: evolution (from left to right) of the intensity of the electron beam at the exit of the slits (left) up to the detection screen located 10 cm after the slits (right). The higher the intensity, the more the color is light blue – Figure in the center: impacts of the electrons observed on the screen – Figure on the right: intensity of the electrons in the ] approximation (on the screen). Numerical data from Claus Jönsson's experiment (1961). Photons, atoms and molecules follow a similar evolution. | |||
| | header = Bohmian trajectories | |||
| | align = center | |||
| | total_width = 900 | |||
| }} | |||
| ==See also== | ==See also== | ||
| {{cols|colwidth=26em}} | |||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * ] | |||
| {{colend}} | |||
| ==References== | ==References== | ||
| {{Reflist}} | |||
| {{reflist|colwidth=30em}} | |||
| ===Further reading=== | ===Further reading=== | ||
| *{{cite book | last = Al-Khalili | first = Jim |author-link=Jim Al-Khalili | title=Quantum: A Guide for the Perplexed | publisher=Weidenfeld |
*{{cite book | last = Al-Khalili | first = Jim |author-link=Jim Al-Khalili | title=Quantum: A Guide for the Perplexed | publisher=Weidenfeld & Nicolson |location=London | year=2003 | isbn=978-0-297-84305-4}} | ||
| *{{cite book | last = |
*{{cite book | last = Ananthaswamy | first = Anil |author-link=Anil Ananthaswamy | title=Through Two Doors at Once: The Elegant Experiment That Captures the Enigma of Our Quantum Reality | publisher=Dutton/Penguin | year=2018 | isbn=978-1-101-98609-7}} | ||
| *{{cite book | last=Feynman | first=Richard P. | title=QED: The Strange Theory of Light and Matter | publisher=Princeton University Press | year=1988 | isbn=978-0-691-02417-2 | url=https://archive.org/details/qedstrangetheory00feyn }} | |||
| *{{cite book | last = Frank| first = Philipp | title=Philosophy of Science | publisher=Prentice-Hall | year=1957}} | *{{cite book | last = Frank| first = Philipp | title=Philosophy of Science | publisher=Prentice-Hall | year=1957}} | ||
| *{{cite book | |
*{{cite book | last1 = French | first1 = A.P. |first2=Edwin F. |last2=Taylor | title= An Introduction to Quantum Physics | publisher=Norton | year=1978 | isbn=978-0-393-09106-9}} | ||
| *{{cite book | last = |
*{{cite book | last = Greene | first = Brian | title = The Elegant Universe | publisher = Vintage | year = 2000 | isbn = 978-0-375-70811-4 | url-access = registration | url = https://archive.org/details/elegantuniverses0000gree }} | ||
| *{{cite book | last = Greene | first = Brian | title= The |
*{{cite book | last = Greene | first = Brian | title = The Fabric of the Cosmos | publisher = Vintage | year = 2005 | isbn = 978-0-375-72720-7 | url-access = registration | url = https://archive.org/details/fabricofcosmossp00gree }} | ||
| *{{cite book | last = |
*{{cite book | last = Gribbin | first = John |author-link=John Gribbin | title=Q is for Quantum: Particle Physics from A to Z | publisher=Weidenfeld & Nicolson | year=1999 | isbn=978-0-7538-0685-2}} | ||
| *{{cite book | last = |
*{{cite book | last = Hey| first = Tony | title=The New Quantum Universe | publisher=Cambridge University Press | year=2003| isbn=978-0-521-56457-1| bibcode = 2003nqu..book.....H }} | ||
| *{{cite book | last = Hey| first = Tony | title=The New Quantum Universe | publisher=Cambridge University Press | year=2003| isbn=0-521-56457-3}} | |||
| *{{cite book | last = Sears | first = Francis Weston | title=Optics | publisher=Addison Wesley | year=1949 }} | *{{cite book | last = Sears | first = Francis Weston | title=Optics | publisher=Addison Wesley | year=1949 }} | ||
| *{{cite book | last = Tipler | first = Paul | title=Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics | edition = 5th | publisher=W. H. Freeman | year=2004 | isbn=0-7167-0810- |
*{{cite book | last = Tipler | first = Paul | title=Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics | edition = 5th | publisher=W. H. Freeman | year=2004 | isbn=978-0-7167-0810-0}} | ||
| ==External links== | ==External links== | ||
| {{Commons category|Double-slit experiments}} | {{Commons category|Double-slit experiments}} | ||
| * by ] of MIT | |||
| * | |||
| * | |||
| ===Interactive animations=== | |||
| * | |||
| * {{Webarchive|url=https://web.archive.org/web/20071028092236/http://www.acoustics.salford.ac.uk/feschools/waves/diffract3.htm |date=28 October 2007 }} | |||
| * | |||
| * | |||
| ===Single particle experiments=== | |||
| * | |||
| * | |||
| * | |||
| * | |||
| * | * | ||
| * | * | ||
| * | |||
| ===Hydrodynamic analog=== | |||
| * | |||
| * | * | ||
| * | |||
| * | |||
| * | |||
| * | |||
| ===Computer simulations=== | |||
| * | |||
| * | * | ||
| * | |||
| {{Quantum mechanics topics}} | |||
| * | |||
| {{Portal bar|Science|Astronomy|Stars|Spaceflight|Outer space|Solar System}} | |||
| *] | |||
| {{Authority control}} | |||
| {{DEFAULTSORT:Double-Slit Experiment}} | {{DEFAULTSORT:Double-Slit Experiment}} | ||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | ] | ||
| {{Link GA|zh}} | |||
Latest revision as of 15:54, 8 December 2024
Physics experiment, showing light and matter can be modelled by both waves and particles "Slit experiment" redirects here. For other uses, see Slit experiment (disambiguation).
 Photons or matter (like electrons) produce an interference pattern when two slits are used
Photons or matter (like electrons) produce an interference pattern when two slits are used Light from a green laser passing through two slits 0.4 mm wide and 0.1 mm apart
Light from a green laser passing through two slits 0.4 mm wide and 0.1 mm apart
In modern physics, the double-slit experiment demonstrates that light and matter can exhibit behavior of both classical particles and classical waves. This type of experiment was first performed by Thomas Young in 1801, as a demonstration of the wave behavior of visible light. In 1927, Davisson and Germer and, independently, George Paget Thomson and his research student Alexander Reid demonstrated that electrons show the same behavior, which was later extended to atoms and molecules. Thomas Young's experiment with light was part of classical physics long before the development of quantum mechanics and the concept of wave–particle duality. He believed it demonstrated that the Christiaan Huygens' wave theory of light was correct, and his experiment is sometimes referred to as Young's experiment or Young's slits.
The experiment belongs to a general class of "double path" experiments, in which a wave is split into two separate waves (the wave is typically made of many photons and better referred to as a wave front, not to be confused with the wave properties of the individual photon) that later combine into a single wave. Changes in the path-lengths of both waves result in a phase shift, creating an interference pattern. Another version is the Mach–Zehnder interferometer, which splits the beam with a beam splitter.
| Part of a series of articles about |
| Quantum mechanics |
|---|
| Schrödinger equation |
| Background |
| Fundamentals |
| Experiments |
| Formulations |
| Equations |
| Interpretations |
| Advanced topics |
Scientists
|
In the basic version of this experiment, a coherent light source, such as a laser beam, illuminates a plate pierced by two parallel slits, and the light passing through the slits is observed on a screen behind the plate. The wave nature of light causes the light waves passing through the two slits to interfere, producing bright and dark bands on the screen – a result that would not be expected if light consisted of classical particles. However, the light is always found to be absorbed at the screen at discrete points, as individual particles (not waves); the interference pattern appears via the varying density of these particle hits on the screen. Furthermore, versions of the experiment that include detectors at the slits find that each detected photon passes through one slit (as would a classical particle), and not through both slits (as would a wave). However, such experiments demonstrate that particles do not form the interference pattern if one detects which slit they pass through. These results demonstrate the principle of wave–particle duality.
Other atomic-scale entities, such as electrons, are found to exhibit the same behavior when fired towards a double slit. Additionally, the detection of individual discrete impacts is observed to be inherently probabilistic, which is inexplicable using classical mechanics.
The experiment can be done with entities much larger than electrons and photons, although it becomes more difficult as size increases. The largest entities for which the double-slit experiment has been performed were molecules that each comprised 2000 atoms (whose total mass was 25,000 atomic mass units).
The double-slit experiment (and its variations) has become a classic for its clarity in expressing the central puzzles of quantum mechanics. Richard Feynman called it "a phenomenon which is impossible to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery ."
Overview

If light consisted strictly of ordinary or classical particles, and these particles were fired in a straight line through a slit and allowed to strike a screen on the other side, we would expect to see a pattern corresponding to the size and shape of the slit. However, when this "single-slit experiment" is actually performed, the pattern on the screen is a diffraction pattern in which the light is spread out. The smaller the slit, the greater the angle of spread. The top portion of the image shows the central portion of the pattern formed when a red laser illuminates a slit and, if one looks carefully, two faint side bands. More bands can be seen with a more highly refined apparatus. Diffraction explains the pattern as being the result of the interference of light waves from the slit.
If one illuminates two parallel slits, the light from the two slits again interferes. Here the interference is a more pronounced pattern with a series of alternating light and dark bands. The width of the bands is a property of the frequency of the illuminating light. (See the bottom photograph to the right.)

When Thomas Young (1773–1829) first demonstrated this phenomenon, it indicated that light consists of waves, as the distribution of brightness can be explained by the alternately additive and subtractive interference of wavefronts. Young's experiment, performed in the early 1800s, played a crucial role in the understanding of the wave theory of light, vanquishing the corpuscular theory of light proposed by Isaac Newton, which had been the accepted model of light propagation in the 17th and 18th centuries.
However, the later discovery of the photoelectric effect demonstrated that under different circumstances, light can behave as if it is composed of discrete particles. These seemingly contradictory discoveries made it necessary to go beyond classical physics and take into account the quantum nature of light.
Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment. He also proposed (as a thought experiment) that if detectors were placed before each slit, the interference pattern would disappear.
The Englert–Greenberger duality relation provides a detailed treatment of the mathematics of double-slit interference in the context of quantum mechanics.
A low-intensity double-slit experiment was first performed by G. I. Taylor in 1909, by reducing the level of incident light until photon emission/absorption events were mostly non-overlapping. A slit interference experiment was not performed with anything other than light until 1961, when Claus Jönsson of the University of Tübingen performed it with coherent electron beams and multiple slits. In 1974, the Italian physicists Pier Giorgio Merli, Gian Franco Missiroli, and Giulio Pozzi performed a related experiment using single electrons from a coherent source and a biprism beam splitter, showing the statistical nature of the buildup of the interference pattern, as predicted by quantum theory. In 2002, the single-electron version of the experiment was voted "the most beautiful experiment" by readers of Physics World. Since that time a number of related experiments have been published, with a little controversy.
In 2012, Stefano Frabboni and co-workers sent single electrons onto nanofabricated slits (about 100 nm wide) and, by detecting the transmitted electrons with a single-electron detector, they could show the build-up of a double-slit interference pattern. Many related experiments involving the coherent interference have been performed; they are the basis of modern electron diffraction, microscopy and high resolution imaging.
In 2018, single particle interference was demonstrated for antimatter in the Positron Laboratory (L-NESS, Politecnico di Milano) of Rafael Ferragut in Como (Italy), by a group led by Marco Giammarchi.
Variations of the experiment
Interference from individual particles
An important version of this experiment involves single particle detection. Illuminating the double-slit with a low intensity results in single particles being detected as white dots on the screen. Remarkably, however, an interference pattern emerges when these particles are allowed to build up one by one (see the image below).
 Experimental electron double slit diffraction pattern. Across the middle of the image at the top, the intensity alternates from high to low, showing interference in the signal from the two slits. Bottom: movie of the pattern being built up dot-by-dot. Click on the thumbnail to enlarge the movie.
Experimental electron double slit diffraction pattern. Across the middle of the image at the top, the intensity alternates from high to low, showing interference in the signal from the two slits. Bottom: movie of the pattern being built up dot-by-dot. Click on the thumbnail to enlarge the movie.
This demonstrates the wave–particle duality, which states that all matter exhibits both wave and particle properties: The particle is measured as a single pulse at a single position, while the modulus squared of the wave describes the probability of detecting the particle at a specific place on the screen giving a statistical interference pattern. This phenomenon has been shown to occur with photons, electrons, atoms, and even some molecules: with buckminsterfullerene (C
60) in 2001, with 2 molecules of 430 atoms (C
60(C
12F
25)
10 and C
168H
94F
152O
8N
4S
4) in 2011, and with molecules of up to 2000 atoms in 2019.
In addition to interference patterns built up from single particles, up to 4 entangled photons can also show interference patterns.
Mach-Zehnder interferometer
Main article: Mach–Zehnder interferometer
The Mach–Zehnder interferometer can be seen as a simplified version of the double-slit experiment. Instead of propagating through free space after the two slits, and hitting any position in an extended screen, in the interferometer the photons can only propagate via two paths, and hit two discrete photodetectors. This makes it possible to describe it via simple linear algebra in dimension 2, rather than differential equations.
A photon emitted by the laser hits the first beam splitter and is then in a superposition between the two possible paths. In the second beam splitter these paths interfere, causing the photon to hit the photodetector on the right with probability one, and the photodetector on the bottom with probability zero. Blocking one of the paths, or equivalently detecting the presence of a photon on a path eliminates interference between the paths: both photodetectors will be hit with probability 1/2. This indicates that after the first beam splitter the photon does not take one path or another, but rather exists in a quantum superposition of the two paths.
"Which-way" experiments and the principle of complementarity
A well-known thought experiment predicts that if particle detectors are positioned at the slits, showing through which slit a photon goes, the interference pattern will disappear. This which-way experiment illustrates the complementarity principle that photons can behave as either particles or waves, but cannot be observed as both at the same time. Despite the importance of this thought experiment in the history of quantum mechanics (for example, see the discussion on Einstein's version of this experiment), technically feasible realizations of this experiment were not proposed until the 1970s. (Naive implementations of the textbook thought experiment are not possible because photons cannot be detected without absorbing the photon.) Currently, multiple experiments have been performed illustrating various aspects of complementarity.
An experiment performed in 1987 produced results that demonstrated that partial information could be obtained regarding which path a particle had taken without destroying the interference altogether. This "wave-particle trade-off" takes the form of an inequality relating the visibility of the interference pattern and the distinguishability of the which-way paths.
Delayed choice and quantum eraser variations
Main article: Delayed-choice quantum eraser
Wheeler's delayed-choice experiments demonstrate that extracting "which path" information after a particle passes through the slits can seem to retroactively alter its previous behavior at the slits.
Quantum eraser experiments demonstrate that wave behavior can be restored by erasing or otherwise making permanently unavailable the "which path" information.
A simple do-it-at-home illustration of the quantum eraser phenomenon was given in an article in Scientific American. If one sets polarizers before each slit with their axes orthogonal to each other, the interference pattern will be eliminated. The polarizers can be considered as introducing which-path information to each beam. Introducing a third polarizer in front of the detector with an axis of 45° relative to the other polarizers "erases" this information, allowing the interference pattern to reappear. This can also be accounted for by considering the light to be a classical wave, and also when using circular polarizers and single photons. Implementations of the polarizers using entangled photon pairs have no classical explanation.
Weak measurement
Main article: Weak measurementIn a highly publicized experiment in 2012, researchers claimed to have identified the path each particle had taken without any adverse effects at all on the interference pattern generated by the particles. In order to do this, they used a setup such that particles coming to the screen were not from a point-like source, but from a source with two intensity maxima. However, commentators such as Svensson have pointed out that there is in fact no conflict between the weak measurements performed in this variant of the double-slit experiment and the Heisenberg uncertainty principle. Weak measurement followed by post-selection did not allow simultaneous position and momentum measurements for each individual particle, but rather allowed measurement of the average trajectory of the particles that arrived at different positions. In other words, the experimenters were creating a statistical map of the full trajectory landscape.
Other variations

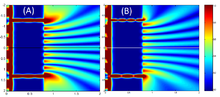
In 1967, Pfleegor and Mandel demonstrated two-source interference using two separate lasers as light sources.
It was shown experimentally in 1972 that in a double-slit system where only one slit was open at any time, interference was nonetheless observed provided the path difference was such that the detected photon could have come from either slit. The experimental conditions were such that the photon density in the system was much less than 1.
In 1991, Carnal and Mlynek performed the classic Young's double slit experiment with metastable helium atoms passing through micrometer-scale slits in gold foil.
In 1999, a quantum interference experiment (using a diffraction grating, rather than two slits) was successfully performed with buckyball molecules (each of which comprises 60 carbon atoms). A buckyball is large enough (diameter about 0.7 nm, nearly half a million times larger than a proton) to be seen in an electron microscope.
In 2002, an electron field emission source was used to demonstrate the double-slit experiment. In this experiment, a coherent electron wave was emitted from two closely located emission sites on the needle apex, which acted as double slits, splitting the wave into two coherent electron waves in a vacuum. The interference pattern between the two electron waves could then be observed. In 2017, researchers performed the double-slit experiment using light-induced field electron emitters. With this technique, emission sites can be optically selected on a scale of ten nanometers. By selectively deactivating (closing) one of the two emissions (slits), researchers were able to show that the interference pattern disappeared.
In 2005, E. R. Eliel presented an experimental and theoretical study of the optical transmission of a thin metal screen perforated by two subwavelength slits, separated by many optical wavelengths. The total intensity of the far-field double-slit pattern is shown to be reduced or enhanced as a function of the wavelength of the incident light beam.
In 2012, researchers at the University of Nebraska–Lincoln performed the double-slit experiment with electrons as described by Richard Feynman, using new instruments that allowed control of the transmission of the two slits and the monitoring of single-electron detection events. Electrons were fired by an electron gun and passed through one or two slits of 62 nm wide × 4 μm tall.
In 2013, a quantum interference experiment (using diffraction gratings, rather than two slits) was successfully performed with molecules that each comprised 810 atoms (whose total mass was over 10,000 atomic mass units). The record was raised to 2000 atoms (25,000 amu) in 2019.
Hydrodynamic pilot wave analogs
Hydrodynamic analogs have been developed that can recreate various aspects of quantum mechanical systems, including single-particle interference through a double-slit. A silicone oil droplet, bouncing along the surface of a liquid, self-propels via resonant interactions with its own wave field. The droplet gently sloshes the liquid with every bounce. At the same time, ripples from past bounces affect its course. The droplet's interaction with its own ripples, which form what is known as a pilot wave, causes it to exhibit behaviors previously thought to be peculiar to elementary particles – including behaviors customarily taken as evidence that elementary particles are spread through space like waves, without any specific location, until they are measured.
Behaviors mimicked via this hydrodynamic pilot-wave system include quantum single particle diffraction, tunneling, quantized orbits, orbital level splitting, spin, and multimodal statistics. It is also possible to infer uncertainty relations and exclusion principles. Videos are available illustrating various features of this system. (See the External links.)
However, more complicated systems that involve two or more particles in superposition are not amenable to such a simple, classically intuitive explanation. Accordingly, no hydrodynamic analog of entanglement has been developed. Nevertheless, optical analogs are possible.
Double-slit experiment on time
In 2023, an experiment was reported recreating an interference pattern in time by shining a pump laser pulse at a screen coated in indium tin oxide (ITO) which would alter the properties of the electrons within the material due to the Kerr effect, changing it from transparent to reflective for around 200 femtoseconds long where a subsequent probe laser beam hitting the ITO screen would then see this temporary change in optical properties as a slit in time and two of them as a double slit with a phase difference adding up destructively or constructively on each frequency component resulting in an interference pattern. Similar results have been obtained classically on water waves.
Classical wave-optics formulation
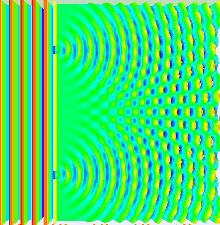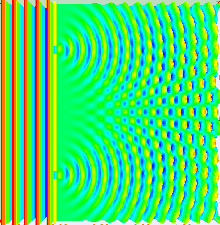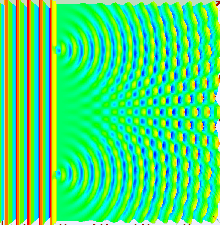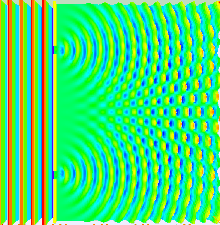


Much of the behaviour of light can be modelled using classical wave theory. The Huygens–Fresnel principle is one such model; it states that each point on a wavefront generates a secondary wavelet, and that the disturbance at any subsequent point can be found by summing the contributions of the individual wavelets at that point. This summation needs to take into account the phase as well as the amplitude of the individual wavelets. Only the intensity of a light field can be measured—this is proportional to the square of the amplitude.
In the double-slit experiment, the two slits are illuminated by the quasi-monochromatic light of a single laser. If the width of the slits is small enough (much less than the wavelength of the laser light), the slits diffract the light into cylindrical waves. These two cylindrical wavefronts are superimposed, and the amplitude, and therefore the intensity, at any point in the combined wavefronts depends on both the magnitude and the phase of the two wavefronts. The difference in phase between the two waves is determined by the difference in the distance travelled by the two waves.
If the viewing distance is large compared with the separation of the slits (the far field), the phase difference can be found using the geometry shown in the figure below right. The path difference between two waves travelling at an angle θ is given by:
Where d is the distance between the two slits. When the two waves are in phase, i.e. the path difference is equal to an integral number of wavelengths, the summed amplitude, and therefore the summed intensity is maximum, and when they are in anti-phase, i.e. the path difference is equal to half a wavelength, one and a half wavelengths, etc., then the two waves cancel and the summed intensity is zero. This effect is known as interference. The interference fringe maxima occur at angles
where λ is the wavelength of the light. The angular spacing of the fringes, θf, is given by
The spacing of the fringes at a distance z from the slits is given by
For example, if two slits are separated by 0.5 mm (d), and are illuminated with a 0.6 μm wavelength laser (λ), then at a distance of 1 m (z), the spacing of the fringes will be 1.2 mm.
If the width of the slits b is appreciable compared to the wavelength, the Fraunhofer diffraction equation is needed to determine the intensity of the diffracted light as follows:
where the sinc function is defined as sinc(x) = sin(x)/x for x ≠ 0, and sinc(0) = 1.
This is illustrated in the figure above, where the first pattern is the diffraction pattern of a single slit, given by the sinc function in this equation, and the second figure shows the combined intensity of the light diffracted from the two slits, where the cos function represents the fine structure, and the coarser structure represents diffraction by the individual slits as described by the sinc function.
Similar calculations for the near field can be made by applying the Fresnel diffraction equation, which implies that as the plane of observation gets closer to the plane in which the slits are located, the diffraction patterns associated with each slit decrease in size, so that the area in which interference occurs is reduced, and may vanish altogether when there is no overlap in the two diffracted patterns.
Path-integral formulation

The double-slit experiment can illustrate the path integral formulation of quantum mechanics provided by Feynman. The path integral formulation replaces the classical notion of a single, unique trajectory for a system, with a sum over all possible trajectories. The trajectories are added together by using functional integration.
Each path is considered equally likely, and thus contributes the same amount. However, the phase of this contribution at any given point along the path is determined by the action along the path:
All these contributions are then added together, and the magnitude of the final result is squared, to get the probability distribution for the position of a particle:
As is always the case when calculating probability, the results must then be normalized by imposing:
The probability distribution of the outcome is the normalized square of the norm of the superposition, over all paths from the point of origin to the final point, of waves propagating proportionally to the action along each path. The differences in the cumulative action along the different paths (and thus the relative phases of the contributions) produces the interference pattern observed by the double-slit experiment. Feynman stressed that his formulation is merely a mathematical description, not an attempt to describe a real process that we can measure.
Interpretations of the experiment
Like the Schrödinger's cat thought experiment, the double-slit experiment is often used to highlight the differences and similarities between the various interpretations of quantum mechanics.
Standard quantum physics
The standard interpretation of the double slit experiment is that the pattern is a wave phenomenon, representing interference between two probability amplitudes, one for each slit. Low intensity experiments demonstrate that the pattern is filled in one particle detection at a time. Any change to the apparatus designed to detect a particle at a particular slit alters the probability amplitudes and the interference disappears. This interpretation is independent of any conscious observer.
Complementarity
Main article: Complementarity (physics)Niels Bohr interpreted quantum experiments like the double-slit experiment using the concept of complementarity. In Bohr's view quantum systems are not classical, but measurements can only give classical results. Certain pairs of classical properties will never be observed in a quantum system simultaneously: the interference pattern of waves in the double slit experiment will disappear if particles are detected at the slits. Modern quantitative versions of the concept allow for a continuous tradeoff between the visibility of the interference fringes and the probability of particle detection at a slit.
Copenhagen interpretation
Main article: Copenhagen interpretationThe Copenhagen interpretation is a collection of views about the meaning of quantum mechanics, stemming from the work of Niels Bohr, Werner Heisenberg, Max Born, and others. The term "Copenhagen interpretation" was apparently coined by Heisenberg during the 1950s to refer to ideas developed in the 1925–1927 period, glossing over his disagreements with Bohr. Consequently, there is no definitive historical statement of what the interpretation entails. Features common across versions of the Copenhagen interpretation include the idea that quantum mechanics is intrinsically indeterministic, with probabilities calculated using the Born rule, and some form of complementarity principle. Moreover, the act of "observing" or "measuring" an object is irreversible, and no truth can be attributed to an object, except according to the results of its measurement. In the Copenhagen interpretation, complementarity means a particular experiment can demonstrate particle behavior (passing through a definite slit) or wave behavior (interference), but not both at the same time. In a Copenhagen-type view, the question of which slit a particle travels through has no meaning when there is no detector.
Relational interpretation
According to the relational interpretation of quantum mechanics, first proposed by Carlo Rovelli, observations such as those in the double-slit experiment result specifically from the interaction between the observer (measuring device) and the object being observed (physically interacted with), not any absolute property possessed by the object. In the case of an electron, if it is initially "observed" at a particular slit, then the observer–particle (photon–electron) interaction includes information about the electron's position. This partially constrains the particle's eventual location at the screen. If it is "observed" (measured with a photon) not at a particular slit but rather at the screen, then there is no "which path" information as part of the interaction, so the electron's "observed" position on the screen is determined strictly by its probability function. This makes the resulting pattern on the screen the same as if each individual electron had passed through both slits.
Many-worlds interpretation
As with Copenhagen, there are multiple variants of the many-worlds interpretation. The unifying theme is that physical reality is identified with a wavefunction, and this wavefunction always evolves unitarily, i.e., following the Schrödinger equation with no collapses. Consequently, there are many parallel universes, which only interact with each other through interference. David Deutsch argues that the way to understand the double-slit experiment is that in each universe the particle travels through a specific slit, but its motion is affected by interference with particles in other universes, and this interference creates the observable fringes. David Wallace, another advocate of the many-worlds interpretation, writes that in the familiar setup of the double-slit experiment the two paths are not sufficiently separated for a description in terms of parallel universes to make sense.
De Broglie–Bohm theory
Main article: de Broglie–Bohm theoryAn alternative to the standard understanding of quantum mechanics, the De Broglie–Bohm theory states that particles also have precise locations at all times, and that their velocities are defined by the wave-function. So while a single particle will travel through one particular slit in the double-slit experiment, the so-called "pilot wave" that influences it will travel through both. The two slit de Broglie-Bohm trajectories were first calculated by Chris Dewdney while working with Chris Philippidis and Basil Hiley at Birkbeck College (London). The de Broglie-Bohm theory produces the same statistical results as standard quantum mechanics, but dispenses with many of its conceptual difficulties by adding complexity through an ad hoc quantum potential to guide the particles.
While the model is in many ways similar to Schrödinger equation, it is known to fail for relativistic cases and does not account for features such as particle creation or annihilation in quantum field theory. Many authors such as nobel laureates Werner Heisenberg, Sir Anthony James Leggett and Sir Roger Penrose have criticized it for not adding anything new.
More complex variants of this type of approach have appeared, for instance the three wave hypothesis of Ryszard Horodecki as well as other complicated combinations of de Broglie and Compton waves. To date there is no evidence that these are useful.
Bohmian trajectories Trajectories of particles in De Broglie–Bohm theory in the double-slit experiment.
Trajectories of particles in De Broglie–Bohm theory in the double-slit experiment. 100 trajectories guided by the wave function. In De Broglie-Bohm's theory, a particle is represented, at any time, by a wave function and a position (center of mass). This is a kind of augmented reality compared to the standard interpretation.
100 trajectories guided by the wave function. In De Broglie-Bohm's theory, a particle is represented, at any time, by a wave function and a position (center of mass). This is a kind of augmented reality compared to the standard interpretation. Numerical simulation of the double-slit experiment with electrons. Figure on the left: evolution (from left to right) of the intensity of the electron beam at the exit of the slits (left) up to the detection screen located 10 cm after the slits (right). The higher the intensity, the more the color is light blue – Figure in the center: impacts of the electrons observed on the screen – Figure on the right: intensity of the electrons in the far field approximation (on the screen). Numerical data from Claus Jönsson's experiment (1961). Photons, atoms and molecules follow a similar evolution.
Numerical simulation of the double-slit experiment with electrons. Figure on the left: evolution (from left to right) of the intensity of the electron beam at the exit of the slits (left) up to the detection screen located 10 cm after the slits (right). The higher the intensity, the more the color is light blue – Figure in the center: impacts of the electrons observed on the screen – Figure on the right: intensity of the electrons in the far field approximation (on the screen). Numerical data from Claus Jönsson's experiment (1961). Photons, atoms and molecules follow a similar evolution.
See also
- Aharonov-Bohm effect
- Complementarity (physics)
- Delayed-choice quantum eraser
- Diffraction from slits
- Dual-polarization interferometry
- Elitzur–Vaidman bomb tester
- N-slit interferometer
- Matter wave
- Photon polarization
- Quantum coherence
- Schrödinger's cat
- Young's interference experiment
- Measurement problem
- Hydrodynamic quantum analogs
- Pilot wave theory
References
- Young, Thomas (1804). "The Bakerian lecture. Experiments and calculation relative to physical optics". Philosophical Transactions of the Royal Society of London. 94: 1–16. doi:10.1098/rstl.1804.0001. S2CID 110408369.
- Navarro, Jaume (2010). "Electron diffraction chez Thomson: early responses to quantum physics in Britain". The British Journal for the History of Science. 43 (2): 245–275. doi:10.1017/S0007087410000026. ISSN 0007-0874. S2CID 171025814.
- Thomson, G. P.; Reid, A. (1927). "Diffraction of Cathode Rays by a Thin Film". Nature. 119 (3007): 890. Bibcode:1927Natur.119Q.890T. doi:10.1038/119890a0. ISSN 0028-0836. S2CID 4122313.
- ^ "Physicists Smash Record For Wave–Particle Duality"
- ^ Eibenberger, Sandra; et al. (2013). "Matter-wave interference with particles selected from a molecular library with masses exceeding 10000 amu". Physical Chemistry Chemical Physics. 15 (35): 14696–14700. arXiv:1310.8343. Bibcode:2013PCCP...1514696E. doi:10.1039/C3CP51500A. PMID 23900710. S2CID 3944699.
- While there is no doubt that Young's demonstration of optical interference, using sunlight, pinholes and cards, played a vital part in the acceptance of the wave theory of light, there is some question as to whether he ever actually performed a double-slit interference experiment.
- Robinson, Andrew (2006). The Last Man Who Knew Everything. New York, NY: Pi Press. pp. 123–124. ISBN 978-0-13-134304-7.
- Kipnis, Naum S. (1991). History of the Principle of Interference of Light. Springer. p. 65. ISBN 978-0-8176-2316-6.
- ^ Lederman, Leon M.; Christopher T. Hill (2011). Quantum Physics for Poets. US: Prometheus Books. pp. 102–111. ISBN 978-1-61614-281-0.
- ^ Feynman, Richard P.; Robert B. Leighton; Matthew Sands (1965). The Feynman Lectures on Physics, Vol. 3. Addison-Wesley. pp. 1.1 – 1.8. ISBN 978-0-201-02118-9.
- Feynman, 1965, p. 1.5
- Darling, David (2007). "Wave–Particle Duality". The Internet Encyclopedia of Science. The Worlds of David Darling. Retrieved 18 October 2008.
- Feynman, 1965, p. 1.7
- Leon Lederman; Christopher T. Hill (27 September 2011). Quantum Physics for Poets. Prometheus Books, Publishers. p. 109. ISBN 978-1-61614-281-0.
- "...if in a double-slit experiment, the detectors which register outcoming photons are placed immediately behind the diaphragm with two slits: A photon is registered in one detector, not in both..." Müller-Kirsten, H. J. W. (2006). Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral. US: World Scientific. p. 14. ISBN 978-981-2566911.
- Plotnitsky, Arkady (2012). Niels Bohr and Complementarity: An Introduction. US: Springer. pp. 75–76. ISBN 978-1-4614-4517-3.
- "It seems that light passes through one slit or the other in the form of photons if we set up an experiment to detect which slit the photon passes, but passes through both slits in the form of a wave if we perform an interference experiment." Rae, Alastair I.M. (2004). Quantum Physics: Illusion Or Reality?. UK: Cambridge University Press. pp. 9–10. ISBN 978-1-139-45527-5.
- Feynman, The Feynman Lectures on Physics, 3:Quantum Mechanics p.1-1 "There is one lucky break, however— electrons behave just like light".
- See: Davisson–Germer experiment Davisson, C. J (1928). "The diffraction of electrons by a crystal of nickel". Bell System Technical Journal. 7: 90–105. doi:10.1002/j.1538-7305.1928.tb00342.x.
- ^ Yaakov Y. Fein; Philipp Geyer; Patrick Zwick; Filip Kiałka; Sebastian Pedalino; Marcel Mayor; Stefan Gerlich; Markus Arndt (September 2019). "Quantum superposition of molecules beyond 25 kDa". Nature Physics. 15 (12): 1242–1245. Bibcode:2019NatPh..15.1242F. doi:10.1038/s41567-019-0663-9. S2CID 203638258.
- Charles Sanders Peirce first proposed the use of this effect as an artifact-independent reference standard for length
- C.S. Peirce (July 1879). "Note on the Progress of Experiments for Comparing a Wave-length with a Meter". American Journal of Science, as referenced by Crease, Robert P. (2011). World in the Balance: The historic quest for an absolute system of measurement. New York: W.W. Norton. p. 317. ISBN 978-0-393-07298-3. p. 203.
- Greene, Brian (1999). The Elegant Universe: Super Strings, Hidden Dimensions, and the Quest for the Ultimate Theory. New York: W.W. Norton. pp. 97–109. ISBN 978-0-393-04688-5.
- Feynman, 1965, chapter 3
- Taylor, G. I. (1909). "Interference Fringes with Feeble Light". Mathematical Proceedings of the Cambridge Philosophical Society. 15: 114. Retrieved 7 December 2024.
- Jönsson, Claus (1 August 1961). "Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten". Zeitschrift für Physik (in German). 161 (4): 454–474. Bibcode:1961ZPhy..161..454J. doi:10.1007/BF01342460. ISSN 0044-3328. S2CID 121659705.
- Jönsson, Claus (1 January 1974). "Electron Diffraction at Multiple Slits". American Journal of Physics. 42 (1): 4–11. Bibcode:1974AmJPh..42....4J. doi:10.1119/1.1987592. ISSN 0002-9505.
- Merli, P G; Missiroli, G F; Pozzi, G (1976). "On the statistical aspect of electron interference phenomena". American Journal of Physics. 44 (3): 306–307. Bibcode:1976AmJPh..44..306M. doi:10.1119/1.10184.
- Rosa, R (2012). "The Merli–Missiroli–Pozzi Two-Slit Electron-Interference Experiment". Physics in Perspective. 14 (2): 178–194. Bibcode:2012PhP....14..178R. doi:10.1007/s00016-011-0079-0. PMC 4617474. PMID 26525832.
- "The most beautiful experiment". Physics World 2002 Archived 24 May 2021 at the Wayback Machine
- Steeds, John; Merli, Pier Giorgio; Pozzi, Giulio; Missiroli, GianFranco; Tonomura, Akira (2003). "The double-slit experiment with single electrons". Physics World. 16 (5): 20–21. doi:10.1088/2058-7058/16/5/24. ISSN 0953-8585.
- Frabboni, Stefano; Gabrielli, Alessandro; Carlo Gazzadi, Gian; Giorgi, Filippo; Matteucci, Giorgio; Pozzi, Giulio; Cesari, Nicola Semprini; Villa, Mauro; Zoccoli, Antonio (May 2012). "The Young-Feynman two-slits experiment with single electrons: Build-up of the interference pattern and arrival-time distribution using a fast-readout pixel detector". Ultramicroscopy. 116: 73–76. doi:10.1016/j.ultramic.2012.03.017. ISSN 0304-3991.
- Cowley, J. M. (1995). Diffraction physics. North Holland personal library (3rd ed.). Amsterdam: Elsevier. ISBN 978-0-444-82218-5.
- Spence, John C. H. (2017). High-resolution electron microscopy (Fourth edition, first published in paperback ed.). Oxford: Oxford University Press. ISBN 978-0-19-879583-4.
- Sala, S.; Ariga, A.; Ereditato, A.; Ferragut, R.; Giammarchi, M.; Leone, M.; Pistillo, C.; Scampoli, P. (2019). "First demonstration of antimatter wave interferometry". Science Advances. 5 (5): eaav7610. Bibcode:2019SciA....5.7610S. doi:10.1126/sciadv.aav7610. PMC 6499593. PMID 31058223.
- Bach, Roger; Pope, Damian; Liou, Sy-Hwang; Batelaan, Herman (13 March 2013). "Controlled double-slit electron diffraction". New Journal of Physics. 15 (3). IOP Publishing: 033018. arXiv:1210.6243. Bibcode:2013NJPh...15c3018B. doi:10.1088/1367-2630/15/3/033018. ISSN 1367-2630. S2CID 832961.
- Greene, Brian (2007). The Fabric of the Cosmos: Space, Time, and the Texture of Reality. Random House LLC. p. 90. ISBN 978-0-307-42853-0.
- Ananthaswamy, Anil (2018). Through Two Doors at Once: The Elegant Experiment That Captures the Enigma of Our Quantum Reality. Penguin. p. 63. ISBN 978-1-101-98611-0.
- Donati, O; Missiroli, G F; Pozzi, G (1973). "An Experiment on Electron Interference". American Journal of Physics. 41 (5): 639–644. Bibcode:1973AmJPh..41..639D. doi:10.1119/1.1987321.
- ^ New Scientist: Quantum wonders: Corpuscles and buckyballs, 2010 (Introduction, subscription needed for full text, quoted in full in Archived 25 September 2017 at the Wayback Machine)
- Wave Particle Duality of C60 Archived 31 March 2012 at the Wayback Machine
- Nairz, Olaf; Brezger, Björn; Arndt, Markus; Zeilinger, Anton (2001). "Diffraction of Complex Molecules by Structures Made of Light". Phys. Rev. Lett. 87 (16): 160401. arXiv:quant-ph/0110012. Bibcode:2001PhRvL..87p0401N. doi:10.1103/physrevlett.87.160401. PMID 11690188. S2CID 21547361.
- Nairz, O; Arndt, M; Zeilinger, A (2003). "Quantum interference experiments with large molecules" (PDF). American Journal of Physics. 71 (4): 319–325. Bibcode:2003AmJPh..71..319N. doi:10.1119/1.1531580. Archived from the original (PDF) on 4 June 2015. Retrieved 4 June 2015.
- Stefan Gerlich; et al. (5 April 2011). "Quantum interference of large organic molecules". Nature Communications. 2: 263. Bibcode:2011NatCo...2..263G. doi:10.1038/ncomms1263. PMC 3104521. PMID 21468015.
- Yaakov Fein; et al. (December 2019). "Quantum superposition of molecules beyond 25kDa". Nature Physics. 15 (12): 1242–1245. Bibcode:2019NatPh..15.1242F. doi:10.1038/s41567-019-0663-9. S2CID 203638258.
- Hessmo, B., M. W. Mitchell, and P. Walther. "Entangled photons show interference and bilocation." CERN Courier (2004): 11.
- Maries, Alexandru; Sayer, Ryan; Singh, Chandralekha (1 July 2020). "Can students apply the concept of "which-path" information learned in the context of Mach–Zehnder interferometer to the double-slit experiment?". American Journal of Physics. 88 (7): 542–550. arXiv:2005.07560. Bibcode:2020AmJPh..88..542M. doi:10.1119/10.0001357. ISSN 0002-9505.
- Marshman, Emily; Singh, Chandralekha (1 March 2016). "Interactive tutorial to improve student understanding of single photon experiments involving a Mach–Zehnder interferometer". European Journal of Physics. 37 (2): 024001. arXiv:1602.06162. Bibcode:2016EJPh...37b4001M. doi:10.1088/0143-0807/37/2/024001. ISSN 0143-0807.
- Vedral, Vlatko (2006). Introduction to Quantum Information Science. Oxford University Press. ISBN 978-0-19-921570-6. OCLC 442351498.
- Harrison, David (2002). "Complementarity and the Copenhagen Interpretation of Quantum Mechanics". UPSCALE. Dept. of Physics, U. of Toronto. Retrieved 21 June 2008.
- Cassidy, David (2008). "Quantum Mechanics 1925–1927: Triumph of the Copenhagen Interpretation". Werner Heisenberg. American Institute of Physics. Archived from the original on 14 January 2016. Retrieved 21 June 2008.
- Boscá Díaz-Pintado, María C. (29–31 March 2007). "Updating the wave–particle duality". 15th UK and European Meeting on the Foundations of Physics. Leeds, UK. Retrieved 21 June 2008.
- Bartell, L. (1980). "Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior". Physical Review D. 21 (6): 1698–1699. Bibcode:1980PhRvD..21.1698B. doi:10.1103/PhysRevD.21.1698.
- ^ Zeilinger, A. (1999). "Experiment and the foundations of quantum physics". Reviews of Modern Physics. 71 (2): S288 – S297. Bibcode:1999RvMPS..71..288Z. doi:10.1103/RevModPhys.71.S288.
- P. Mittelstaedt; A. Prieur; R. Schieder (1987). "Unsharp particle-wave duality in a photon split-beam experiment". Foundations of Physics. 17 (9): 891–903. Bibcode:1987FoPh...17..891M. doi:10.1007/BF00734319. S2CID 122856271.
- D.M. Greenberger and A. Yasin, "Simultaneous wave and particle knowledge in a neutron interferometer", Physics Letters A 128, 391–4 (1988).
- Sen, D. (2014). "The uncertainty relations in quantum mechanics". Current Science. 107 (2): 203–218. ISSN 0011-3891. JSTOR 24103129.
"However, the 'wave-particle trade-off is now expressed in terms of an inequality, known as Englert-Greenberger duality or simply wave-particle duality relation". See also ref 24 in this work.
- ^ Hillmer, R.; Kwiat, P. (2007). "A do-it-yourself quantum eraser". Scientific American. Vol. 296, no. 5. pp. 90–95. Bibcode:2007SciAm.296e..90H. doi:10.1038/scientificamerican0507-90. Retrieved 11 January 2016.
- ^ Chiao, R. Y.; P. G. Kwiat; Steinberg, A. M. (1995). "Quantum non-locality in two-photon experiments at Berkeley". Quantum and Semiclassical Optics: Journal of the European Optical Society Part B. 7 (3): 259–278. arXiv:quant-ph/9501016. Bibcode:1995QuSOp...7..259C. doi:10.1088/1355-5111/7/3/006. S2CID 118987962.
- Francis, Matthew (21 May 2012). "Disentangling the wave–particle duality in the double-slit experiment". Ars Technica.
- ^ Svensson, Bengt E. Y. (2013). "Pedagogical Review of Quantum Measurement Theory with an Emphasis on Weak Measurements". Quanta. 2 (1): 18–49. arXiv:1202.5148. doi:10.12743/quanta.v2i1.12. S2CID 119242577.
- Pfleegor, R. L.; Mandel, L. (July 1967). "Interference of Independent Photon Beams". Physical Review. 159 (5): 1084–1088. Bibcode:1967PhRv..159.1084P. doi:10.1103/PhysRev.159.1084.
- "Interference of Independent Photon Beams: The Pfleegor-Mandel Experiment". Archived from the original on 3 January 2011. Retrieved 16 June 2011.>
- Sillitto, R.M.; Wykes, Catherine (1972). "An interference experiment with light beams modulated in anti-phase by an electro-optic shutter". Physics Letters A. 39 (4): 333–334. Bibcode:1972PhLA...39..333S. doi:10.1016/0375-9601(72)91015-8.
- ""To a light particle"".
- Carnal, O.; Mlynek, J. (May 1991). "Young's Double-Slit Experiment with Atoms: A Simple Atom Interferometer". Physical Review Letters. 66 (21): 2689–2694. Bibcode:1991PhRvL..66.2689C. doi:10.1103/PhysRevLett.66.2689. PMID 10043591.
- Carnal, O.; Mlynek, J. (1991). "Young's Double-Slit Experiment with Atoms: A Simple Atom Interferometer". Physical Review Letters. 66 (21): 2689–2692. Bibcode:1991PhRvL..66.2689C. doi:10.1103/PhysRevLett.66.2689. PMID 10043591. Retrieved 20 March 2022.>
- Arndt, Markus; Nairz, Olaf; Vos-Andreae, Julian; Keller, Claudia; Van Der Zouw, Gerbrand; Zeilinger, Anton (1999). "Wave–particle duality of C60 molecules". Nature. 401 (6754): 680–682. Bibcode:1999Natur.401..680A. doi:10.1038/44348. PMID 18494170. S2CID 4424892.
- Oshima, C.; Mastuda, K.; Kona, T.; Mogami, Y.; Komaki, M.; Murata, Y.; Yamashita, T.; Kuzumaki, T.; Horiike, Y. (4 January 2002). "Young's Interference of Electrons in Field Emission Patterns". Physical Review Letters. 88 (3): 038301. Bibcode:2002PhRvL..88c8301O. doi:10.1103/PhysRevLett.88.038301. ISSN 0031-9007. PMID 11801091.
- Yanagisawa, Hirofumi; Ciappina, Marcelo; Hafner, Christian; Schötz, Johannes; Osterwalder, Jürg; Kling, Matthias F. (4 October 2017). "Optical Control of Young's Type Double-slit Interferometer for Laser-induced Electron Emission from a Nano-tip". Scientific Reports. 7 (1): 12661. arXiv:1710.02216. Bibcode:2017NatSR...712661Y. doi:10.1038/s41598-017-12832-3. ISSN 2045-2322. PMC 5627254. PMID 28978914.
- Schouten, H.F.; Kuzmin, N.; Dubois, G.; Visser, T.D.; Gbur, G.; Alkemade, P.F.A.; Blok, H.; Hooft, G.W.; Lenstra, D.; Eliel, E.R. (7 February 2005). "Plasmon-Assisted Two-Slit Transmission: Young's Experiment Revisited". Phys. Rev. Lett. 94 (5): 053901. Bibcode:2005PhRvL..94e3901S. doi:10.1103/physrevlett.94.053901. hdl:1887/71482. PMID 15783641. S2CID 19197175.
- Bach, Roger; et al. (March 2013). "Controlled double-slit electron diffraction". New Journal of Physics. 15 (3): 033018. arXiv:1210.6243. Bibcode:2013NJPh...15c3018B. doi:10.1088/1367-2630/15/3/033018. S2CID 832961.
- ^ Bush, John WM (2015). "Pilot-wave hydrodynamics" (PDF). Annual Review of Fluid Mechanics. 47 (1): 269–292. Bibcode:2015AnRFM..47..269B. doi:10.1146/annurev-fluid-010814-014506. hdl:1721.1/89790. Archived (PDF) from the original on 21 June 2015. Retrieved 21 June 2015.
- Bush, John W. M. (2010). "Quantum mechanics writ large". PNAS. 107 (41): 17455–17456. Bibcode:2010PNAS..10717455B. doi:10.1073/pnas.1012399107. PMC 2955131.
- Natalie Wolchover (30 June 2014). "Have We Been Interpreting Quantum Mechanics Wrong This Whole Time?". Wired.
- Couder, Y.; Fort, E. (2012). "Probabilities and trajectories in a classical wave–particle duality". Journal of Physics: Conference Series. 361 (1): 012001. Bibcode:2012JPhCS.361a2001C. doi:10.1088/1742-6596/361/1/012001.
- Baggott, Jim (2011). The Quantum Story: A History in 40 Moments. New York: Oxford University Press. pp. 76. ("The wavefunction of a system containing N particles depends on 3N position coordinates and is a function in a 3N-dimensional configuration space or 'phase space'. It is difficult to visualize a reality comprising imaginary functions in an abstract, multi-dimensional space. No difficulty arises, however, if the imaginary functions are not to be given a real interpretation.")
- Li, Pengyun; Sun, Yifan; Yang, Zhenwei; Song, Xinbing; Zhang, Xiangdong (2016). "Classical hypercorrelation and wave-optics analogy of quantum superdense coding". Scientific Reports. 5: 18574. Bibcode:2015NatSR...518574L. doi:10.1038/srep18574. PMC 4686973. PMID 26689679.
- ^ Bacot, Vincent; Labousse, Matthieu; Eddi, Antonin; Fink, Mathias; Fort, Emmanuel (November 2016). "Time reversal and holography with spacetime transformations". Nature Physics. 12 (10): 972–977. arXiv:1510.01277. Bibcode:2016NatPh..12..972B. doi:10.1038/nphys3810. ISSN 1745-2481. S2CID 53536274.
- Rodríguez-Fortuño, Francisco J. (3 April 2023). "An optical double-slit experiment in time". Nature Physics. 19 (7): 929–930. Bibcode:2023NatPh..19..929R. doi:10.1038/s41567-023-02026-2. ISSN 1745-2481. S2CID 257945438.
- ^ Castelvecchi, Davide (3 April 2023). "Light waves squeezed through 'slits in time'". Nature. 616 (7956): 230. Bibcode:2023Natur.616..230C. doi:10.1038/d41586-023-00968-4. PMID 37012471. S2CID 257922697.
- Jenkins FA and White HE, Fundamentals of Optics, 1967, McGraw Hill, New York
- Longhurst RS, Physical and Geometrical Optics, 1967, 2nd Edition, Longmans
- Zee, Anthony (2010). Quantum Field Theory in a Nutshell (2nd ed.). Princeton University Press. pp. 2–16. ISBN 978-0-691-14034-6.
- Mandel, L. (1 March 1999). "Quantum effects in one-photon and two-photon interference". Reviews of Modern Physics. 71 (2): S274 – S282. Bibcode:1999RvMPS..71..274M. doi:10.1103/RevModPhys.71.S274. ISSN 0034-6861.
- ^ Faye, Jan (2019). "Copenhagen Interpretation of Quantum Mechanics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- Wootters, William K.; Zurek, Wojciech H. (15 January 1979). "Complementarity in the double-slit experiment: Quantum nonseparability and a quantitative statement of Bohr's principle". Physical Review D. 19 (2): 473–484. Bibcode:1979PhRvD..19..473W. doi:10.1103/PhysRevD.19.473. ISSN 0556-2821.
- Bartell, L. S. (15 March 1980). "Complementarity in the double-slit experiment: On simple realizable systems for observing intermediate particle-wave behavior". Physical Review D. 21 (6): 1698–1699. Bibcode:1980PhRvD..21.1698B. doi:10.1103/PhysRevD.21.1698. ISSN 0556-2821.
- Camilleri, K.; Schlosshauer, M. (2015). "Niels Bohr as Philosopher of Experiment: Does Decoherence Theory Challenge Bohr's Doctrine of Classical Concepts?". Studies in History and Philosophy of Modern Physics. 49: 73–83. arXiv:1502.06547. Bibcode:2015SHPMP..49...73C. doi:10.1016/j.shpsb.2015.01.005. S2CID 27697360.
- Scheibe, Erhard (1973). The Logical Analysis of Quantum Mechanics. Pergamon Press. ISBN 978-0-08-017158-6. OCLC 799397091.
here is no point in looking for the Copenhagen interpretation as a unified and consistent logical structure. Terms such as "Copenhagen interpretation" or "Copenhagen school" are based on the history of the development of quantum mechanics; they form a simplified and often convenient way of referring to the ideas of a number of physicists who played an important role in the establishment of quantum mechanics, and who were collaborators of Bohr's at his Institute or took part in the discussions during the crucial years. On closer inspection, one sees quite easily that these ideas are divergent in detail and that in particular the views of Bohr, the spiritual leader of the school, form a separate entity which can now be understood only by a thorough study of as many as possible of the relevant publications by Bohr himself.
- Mermin, N. David (1 January 2017). "Why QBism Is Not the Copenhagen Interpretation and What John Bell Might Have Thought of It". In Bertlmann, Reinhold; Zeilinger, Anton (eds.). Quantum Speakables II. The Frontiers Collection. Springer International Publishing. pp. 83–93. arXiv:1409.2454. doi:10.1007/978-3-319-38987-5_4. ISBN 978-3-319-38985-1. S2CID 118458259.
- ^ Omnès, Roland (1999). "The Copenhagen Interpretation". Understanding Quantum Mechanics. Princeton University Press. doi:10.2307/j.ctv173f2pm.9. S2CID 203390914.
- Rosenfeld, L. (1953). "Strife about Complementarity". Science Progress (1933– ). 41 (163): 393–410. ISSN 0036-8504. JSTOR 43414997.
- Peres, Asher (1995). Quantum Theory: Concepts and Methods. Kluwer Academic Publishers. pp. 36–39. ISBN 0-7923-2549-4.
- Omnès, R. (1994). The Interpretation of Quantum Mechanics. Princeton University Press. p. 167. ISBN 978-0-691-03669-4. OCLC 439453957.
- Brukner, Časlav; Zeilinger, Anton (2005). "Quantum Physics as a Science of Information". In Elitzur, Avshalom C.; Dolev, Shahar; Kolenda, Nancy (eds.). Quo Vadis Quantum Mechanics?. Berlin, Heidelberg: Springer. pp. 47–61. doi:10.1007/3-540-26669-0_3. ISBN 978-3-540-22188-3.
- Rovelli, Carlo (1996). "Relational Quantum Mechanics". International Journal of Theoretical Physics. 35 (8): 1637–1678. arXiv:quant-ph/9609002. Bibcode:1996IJTP...35.1637R. doi:10.1007/BF02302261. S2CID 16325959.
- Kent, Adrian (February 2015). "Does it Make Sense to Speak of Self-Locating Uncertainty in the Universal Wave Function? Remarks on Sebens and Carroll". Foundations of Physics. 45 (2): 211–217. arXiv:1408.1944. Bibcode:2015FoPh...45..211K. doi:10.1007/s10701-014-9862-5. ISSN 0015-9018. S2CID 118471198.
- Vaidman, Lev (5 August 2021). "Many-Worlds Interpretation of Quantum Mechanics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- Deutsch, David (1998). The Fabric of Reality. London: Penguin. pp. 40–53. ISBN 978-0-14-014690-5.
- Wallace, David (2012). The Emergent Multiverse. Oxford: Oxford University Press. p. 382. ISBN 978-0-19-954696-1.
- Philippidis, C.; Dewdney, C.; Hiley, B. J. (1979). "Quantum interference and the quantum potential". Il Nuovo Cimento B. 52 (1): 15–28. Bibcode:1979NCimB..52...15P. doi:10.1007/bf02743566. ISSN 1826-9877. S2CID 53575967.
- "Bohmian Mechanics". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. 2017.
- Goldstein, Sheldon (2021), "Bohmian Mechanics", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Fall 2021 ed.), Metaphysics Research Lab, Stanford University, retrieved 14 August 2023
- Heisenberg, W. (1956). Pauli, W (ed.). "Niels Bohr and the Development of Physics: Essays Dedicated to Niels Bohr on the Occasion of his Seventieth Birthday". Physics Today. 9 (8): 12. doi:10.1063/1.3060063. ISSN 0031-9228.
- Leggett, A J (2002). "Testing the limits of quantum mechanics: motivation, state of play, prospects". Journal of Physics: Condensed Matter. 14 (15): R415 – R451. doi:10.1088/0953-8984/14/15/201. ISSN 0953-8984. S2CID 250911999.
- Penrose, Roger (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. London: Cape. ISBN 978-0-224-04447-9.
- Horodecki, R. (1981). "De broglie wave and its dual wave". Physics Letters A. 87 (3): 95–97. Bibcode:1981PhLA...87...95H. doi:10.1016/0375-9601(81)90571-5. ISSN 0375-9601.
- Horodecki, R. (1983). "Superluminal singular dual wave". Lettere al Nuovo Cimento. 36 (15): 509–511. doi:10.1007/bf02817964. ISSN 1827-613X. S2CID 120784358.
- Das, S.N. (1984). "De Broglie wave and Compton wave". Physics Letters A. 102 (8): 338–339. Bibcode:1984PhLA..102..338D. doi:10.1016/0375-9601(84)90291-3. ISSN 0375-9601.
- Mukhopadhyay, P. (1986). "A correlation between the compton wavelength and the de Broglie wavelength". Physics Letters A. 114 (4): 179–182. Bibcode:1986PhLA..114..179M. doi:10.1016/0375-9601(86)90200-8. ISSN 0375-9601.
- Elbaz, Claude (1985). "On de Broglie waves and Compton waves of massive particles". Physics Letters A. 109 (1–2): 7–8. Bibcode:1985PhLA..109....7E. doi:10.1016/0375-9601(85)90379-2. ISSN 0375-9601.
Further reading
- Al-Khalili, Jim (2003). Quantum: A Guide for the Perplexed. London: Weidenfeld & Nicolson. ISBN 978-0-297-84305-4.
- Ananthaswamy, Anil (2018). Through Two Doors at Once: The Elegant Experiment That Captures the Enigma of Our Quantum Reality. Dutton/Penguin. ISBN 978-1-101-98609-7.
- Feynman, Richard P. (1988). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 978-0-691-02417-2.
- Frank, Philipp (1957). Philosophy of Science. Prentice-Hall.
- French, A.P.; Taylor, Edwin F. (1978). An Introduction to Quantum Physics. Norton. ISBN 978-0-393-09106-9.
- Greene, Brian (2000). The Elegant Universe. Vintage. ISBN 978-0-375-70811-4.
- Greene, Brian (2005). The Fabric of the Cosmos. Vintage. ISBN 978-0-375-72720-7.
- Gribbin, John (1999). Q is for Quantum: Particle Physics from A to Z. Weidenfeld & Nicolson. ISBN 978-0-7538-0685-2.
- Hey, Tony (2003). The New Quantum Universe. Cambridge University Press. Bibcode:2003nqu..book.....H. ISBN 978-0-521-56457-1.
- Sears, Francis Weston (1949). Optics. Addison Wesley.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 978-0-7167-0810-0.
External links
- Double slit interference lecture by Walter Lewin of MIT
Interactive animations
- Huygens and interference Archived 28 October 2007 at the Wayback Machine
Single particle experiments
- Website with the movie and other information from the first single electron experiment by Merli, Missiroli, and Pozzi.
- Movie showing single electron events build up to form an interference pattern in double-slit experiments. Several versions with and without narration (File size = 3.6 to 10.4 MB) (Movie Length = 1m 8s)
- Freeview video 'Electron Waves Unveil the Microcosmos' A Royal Institution Discourse by Akira Tonomura provided by the Vega Science Trust
- Hitachi website that provides background on Tonomura video and link to the video
Hydrodynamic analog
- "Single-particle interference observed for macroscopic objects"
- Pilot-Wave Hydrodynamics: Supplemental Video
- Through the Wormhole: Yves Couder . Explains Wave/Particle Duality via Silicon Droplets
Computer simulations
- Java demonstration of Young's double slit interference
- A simulation that runs in Mathematica Player, in which the number of quantum particles, the frequency of the particles, and the slit separation can be independently varied








