Misplaced Pages

Latest revision as of 11:17, 17 December 2024

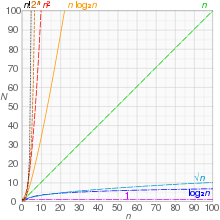
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor.

Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally expressed as a function of the size of the input. Since this function is generally difficult to compute exactly, and the running time for small inputs is usually not consequential, one commonly focuses on the behavior of the complexity when the input size increases—that is, the asymptotic behavior of the complexity. Therefore, the time complexity is commonly expressed using big O notation, typically ${\displaystyle O(n)}$, ${\displaystyle O(n\log n)}$, ${\displaystyle O(n^{\alpha })}$, ${\displaystyle O(2^{n})}$, etc., where n is the size in units of bits needed to represent the input.

Algorithmic complexities are classified according to the type of function appearing in the big O notation. For example, an algorithm with time complexity ${\displaystyle O(n)}$ is a linear time algorithm and an algorithm with time complexity ${\displaystyle O(n^{\alpha })}$ for some constant ${\displaystyle \alpha >0}$ is a polynomial time algorithm.

Table of common time complexities

The following table summarizes some classes of commonly encountered time complexities. In the table, poly(x) = x, i.e., polynomial in x.

Name	Complexity class	Time complexity (O(n))	Examples of running times	Example algorithms
constant time		${\displaystyle O(1)}$	10	Finding the median value in a sorted array of numbers. Calculating (−1).
inverse Ackermann time		${\displaystyle O{\bigl (}\alpha (n){\bigr )}}$		Amortized time per operation using a disjoint set
iterated logarithmic time		${\displaystyle O(\log ^{*}n)}$		Distributed coloring of cycles
log-logarithmic		${\displaystyle O(\log \log n)}$		Amortized time per operation using a bounded priority queue
logarithmic time	DLOGTIME	${\displaystyle O(\log n)}$	${\displaystyle \log n}$, ${\displaystyle \log(n^{2})}$	Binary search
polylogarithmic time		${\displaystyle {\text{poly}}(\log n)}$	${\displaystyle (\log n)^{2}}$
fractional power		${\displaystyle O(n^{c})}$ where ${\displaystyle 0<c<1}$	${\displaystyle n^{\frac {1}{2}}}$, ${\displaystyle n^{\frac {2}{3}}}$	Range searching in a k-d tree
linear time		${\displaystyle O(n)}$	n, ${\displaystyle 2n+5}$	Finding the smallest or largest item in an unsorted array. Kadane's algorithm. Linear search.
"n log-star n" time		${\displaystyle O(n\log ^{*}n)}$		Seidel's polygon triangulation algorithm.
linearithmic time		${\displaystyle O(n\log n)}$	${\displaystyle n\log n}$, ${\displaystyle \log n!}$	Fastest possible comparison sort. Fast Fourier transform.
quasilinear time		${\displaystyle n{\text{poly}}(\log n)}$	${\displaystyle n\log ^{2}n}$	Multipoint polynomial evaluation
quadratic time		${\displaystyle O(n^{2})}$	${\displaystyle n^{2}}$	Bubble sort. Insertion sort. Direct convolution
cubic time		${\displaystyle O(n^{3})}$	${\displaystyle n^{3}}$	Naive multiplication of two ${\displaystyle n\times n}$ matrices. Calculating partial correlation.
polynomial time	P	${\displaystyle 2^{O(\log n)}={\text{poly}}(n)}$	${\displaystyle n^{2}+n}$, ${\displaystyle n^{10}}$	Karmarkar's algorithm for linear programming. AKS primality test
quasi-polynomial time	QP	${\displaystyle 2^{{\text{poly}}(\log n)}}$	${\displaystyle n^{\log \log n}}$, ${\displaystyle n^{\log n}}$	Best-known O(logn)-approximation algorithm for the directed Steiner tree problem, best known parity game solver, best known graph isomorphism algorithm
sub-exponential time (first definition)	SUBEXP	${\displaystyle O(2^{n^{\epsilon }})}$ for all ${\displaystyle 0<\epsilon <1}$		Contains BPP unless EXPTIME (see below) equals MA.
sub-exponential time (second definition)		${\displaystyle 2^{o(n)}}$	${\displaystyle 2^{\sqrt{n}}}$	Best classical algorithm for integer factorization formerly-best algorithm for graph isomorphism
exponential time (with linear exponent)	E	${\displaystyle 2^{O(n)}}$	${\displaystyle 1.1^{n}}$, ${\displaystyle 10^{n}}$	Solving the traveling salesman problem using dynamic programming
factorial time		${\displaystyle O(n)!=2^{O(n\log n)}}$	${\displaystyle n!,n^{n},2^{n\log n}}$	Solving the traveling salesman problem via brute-force search
exponential time	EXPTIME	${\displaystyle 2^{{\text{poly}}(n)}}$	${\displaystyle 2^{n}}$, ${\displaystyle 2^{n^{2}}}$	Solving matrix chain multiplication via brute-force search
double exponential time	2-EXPTIME	${\displaystyle 2^{2^{{\text{poly}}(n)}}}$	${\displaystyle 2^{2^{n}}}$	Deciding the truth of a given statement in Presburger arithmetic

Constant time

An algorithm is said to be constant time (also written as ${\textstyle O(1)}$ time) if the value of ${\textstyle T(n)}$ (the complexity of the algorithm) is bounded by a value that does not depend on the size of the input. For example, accessing any single element in an array takes constant time as only one operation has to be performed to locate it. In a similar manner, finding the minimal value in an array sorted in ascending order; it is the first element. However, finding the minimal value in an unordered array is not a constant time operation as scanning over each element in the array is needed in order to determine the minimal value. Hence it is a linear time operation, taking ${\textstyle O(n)}$ time. If the number of elements is known in advance and does not change, however, such an algorithm can still be said to run in constant time.

Despite the name "constant time", the running time does not have to be independent of the problem size, but an upper bound for the running time has to be independent of the problem size. For example, the task "exchange the values of a and b if necessary so that ${\textstyle a\leq b}$" is called constant time even though the time may depend on whether or not it is already true that ${\textstyle a\leq b}$. However, there is some constant t such that the time required is always at most t.

Logarithmic time

An algorithm is said to take logarithmic time when ${\displaystyle T(n)=O(\log n)}$. Since ${\displaystyle \log _{a}n}$ and ${\displaystyle \log _{b}n}$ are related by a constant multiplier, and such a multiplier is irrelevant to big O classification, the standard usage for logarithmic-time algorithms is ${\displaystyle O(\log n)}$ regardless of the base of the logarithm appearing in the expression of T.

Algorithms taking logarithmic time are commonly found in operations on binary trees or when using binary search.

An ${\displaystyle O(\log n)}$ algorithm is considered highly efficient, as the ratio of the number of operations to the size of the input decreases and tends to zero when n increases. An algorithm that must access all elements of its input cannot take logarithmic time, as the time taken for reading an input of size n is of the order of n.

An example of logarithmic time is given by dictionary search. Consider a dictionary D which contains n entries, sorted in alphabetical order. We suppose that, for ${\displaystyle 1\leq k\leq n}$, one may access the kth entry of the dictionary in a constant time. Let ${\displaystyle D(k)}$ denote this kth entry. Under these hypotheses, the test to see if a word w is in the dictionary may be done in logarithmic time: consider ${\displaystyle D\left(\left\lfloor {\frac {n}{2}}\right\rfloor \right)}$, where ${\displaystyle \lfloor \;\rfloor }$ denotes the floor function. If ${\displaystyle w=D\left(\left\lfloor {\frac {n}{2}}\right\rfloor \right)}$--that is to say, the word w is exactly in the middle of the dictionary--then we are done. Else, if ${\displaystyle w<D\left(\left\lfloor {\frac {n}{2}}\right\rfloor \right)}$--i.e., if the word w comes earlier in alphabetical order than the middle word of the whole dictionary--we continue the search in the same way in the left (i.e. earlier) half of the dictionary, and then again repeatedly until the correct word is found. Otherwise, if it comes after the middle word, continue similarly with the right half of the dictionary. This algorithm is similar to the method often used to find an entry in a paper dictionary. As a result, the search space within the dictionary decreases as the algorithm gets closer to the target word.

Polylogarithmic time

An algorithm is said to run in polylogarithmic time if its time ${\displaystyle T(n)}$ is ${\displaystyle O{\bigl (}(\log n)^{k}{\bigr )}}$ for some constant k. Another way to write this is ${\displaystyle O(\log ^{k}n)}$.

For example, matrix chain ordering can be solved in polylogarithmic time on a parallel random-access machine, and a graph can be determined to be planar in a fully dynamic way in ${\displaystyle O(\log ^{3}n)}$ time per insert/delete operation.

Sub-linear time

An algorithm is said to run in sub-linear time (often spelled sublinear time) if ${\displaystyle T(n)=o(n)}$. In particular this includes algorithms with the time complexities defined above.

The specific term sublinear time algorithm commonly refers to randomized algorithms that sample a small fraction of their inputs and process them efficiently to approximately infer properties of the entire instance. This type of sublinear time algorithm is closely related to property testing and statistics.

Other settings where algorithms can run in sublinear time include:

• Parallel algorithms that have linear or greater total work (allowing them to read the entire input), but sub-linear depth.
• Algorithms that have guaranteed assumptions on the input structure. An important example are operations on data structures, e.g. binary search in a sorted array.
• Algorithms that search for local structure in the input, for example finding a local minimum in a 1-D array (can be solved in ${\displaystyle O(\log(n))}$ time using a variant of binary search).  A closely related notion is that of Local Computation Algorithms (LCA) where the algorithm receives a large input and queries to local information about some valid large output.

Linear time

An algorithm is said to take linear time, or ${\displaystyle O(n)}$ time, if its time complexity is ${\displaystyle O(n)}$. Informally, this means that the running time increases at most linearly with the size of the input. More precisely, this means that there is a constant c such that the running time is at most ${\displaystyle cn}$ for every input of size n. For example, a procedure that adds up all elements of a list requires time proportional to the length of the list, if the adding time is constant, or, at least, bounded by a constant.

Linear time is the best possible time complexity in situations where the algorithm has to sequentially read its entire input. Therefore, much research has been invested into discovering algorithms exhibiting linear time or, at least, nearly linear time. This research includes both software and hardware methods. There are several hardware technologies which exploit parallelism to provide this. An example is content-addressable memory. This concept of linear time is used in string matching algorithms such as the Boyer–Moore string-search algorithm and Ukkonen's algorithm.

Quasilinear time

An algorithm is said to run in quasilinear time (also referred to as log-linear time) if ${\displaystyle T(n)=O(n\log ^{k}n)}$ for some positive constant k; linearithmic time is the case ${\displaystyle k=1}$. Using soft O notation these algorithms are ${\displaystyle {\tilde {O}}(n)}$. Quasilinear time algorithms are also ${\displaystyle O(n^{1+\varepsilon })}$ for every constant ${\displaystyle \varepsilon >0}$ and thus run faster than any polynomial time algorithm whose time bound includes a term ${\displaystyle n^{c}}$ for any ${\displaystyle c>1}$.

Algorithms which run in quasilinear time include:

• In-place merge sort, ${\displaystyle O(n\log ^{2}n)}$
• Quicksort, ${\displaystyle O(n\log n)}$, in its randomized version, has a running time that is ${\displaystyle O(n\log n)}$ in expectation on the worst-case input. Its non-randomized version has an ${\displaystyle O(n\log n)}$ running time only when considering average case complexity.
• Heapsort, ${\displaystyle O(n\log n)}$, merge sort, introsort, binary tree sort, smoothsort, patience sorting, etc. in the worst case
• Fast Fourier transforms, ${\displaystyle O(n\log n)}$
• Monge array calculation, ${\displaystyle O(n\log n)}$

In many cases, the ${\displaystyle O(n\log n)}$ running time is simply the result of performing a ${\displaystyle \Theta (\log n)}$ operation n times (for the notation, see Big O notation § Family of Bachmann–Landau notations). For example, binary tree sort creates a binary tree by inserting each element of the n-sized array one by one. Since the insert operation on a self-balancing binary search tree takes ${\displaystyle O(\log n)}$ time, the entire algorithm takes ${\displaystyle O(n\log n)}$ time.

Comparison sorts require at least ${\displaystyle \Omega (n\log n)}$ comparisons in the worst case because ${\displaystyle \log(n!)=\Theta (n\log n)}$, by Stirling's approximation. They also frequently arise from the recurrence relation ${\textstyle T(n)=2T\left({\frac {n}{2}}\right)+O(n)}$.

Sub-quadratic time

An algorithm is said to be subquadratic time if ${\displaystyle T(n)=o(n^{2})}$.

For example, simple, comparison-based sorting algorithms are quadratic (e.g. insertion sort), but more advanced algorithms can be found that are subquadratic (e.g. shell sort). No general-purpose sorts run in linear time, but the change from quadratic to sub-quadratic is of great practical importance.

Polynomial time

An algorithm is said to be of polynomial time if its running time is upper bounded by a polynomial expression in the size of the input for the algorithm, that is, T(n) = O(n) for some positive constant k. Problems for which a deterministic polynomial-time algorithm exists belong to the complexity class P, which is central in the field of computational complexity theory. Cobham's thesis states that polynomial time is a synonym for "tractable", "feasible", "efficient", or "fast".

Some examples of polynomial-time algorithms:

• The selection sort sorting algorithm on n integers performs ${\displaystyle An^{2}}$ operations for some constant A. Thus it runs in time ${\displaystyle O(n^{2})}$ and is a polynomial-time algorithm.
• All the basic arithmetic operations (addition, subtraction, multiplication, division, and comparison) can be done in polynomial time.
• Maximum matchings in graphs can be found in polynomial time. In some contexts, especially in optimization, one differentiates between strongly polynomial time and weakly polynomial time algorithms.

These two concepts are only relevant if the inputs to the algorithms consist of integers.

Complexity classes

The concept of polynomial time leads to several complexity classes in computational complexity theory. Some important classes defined using polynomial time are the following.

• P: The complexity class of decision problems that can be solved on a deterministic Turing machine in polynomial time
• NP: The complexity class of decision problems that can be solved on a non-deterministic Turing machine in polynomial time
• ZPP: The complexity class of decision problems that can be solved with zero error on a probabilistic Turing machine in polynomial time
• RP: The complexity class of decision problems that can be solved with 1-sided error on a probabilistic Turing machine in polynomial time.
• BPP: The complexity class of decision problems that can be solved with 2-sided error on a probabilistic Turing machine in polynomial time
• BQP: The complexity class of decision problems that can be solved with 2-sided error on a quantum Turing machine in polynomial time

P is the smallest time-complexity class on a deterministic machine which is robust in terms of machine model changes. (For example, a change from a single-tape Turing machine to a multi-tape machine can lead to a quadratic speedup, but any algorithm that runs in polynomial time under one model also does so on the other.) Any given abstract machine will have a complexity class corresponding to the problems which can be solved in polynomial time on that machine.

Superpolynomial time

An algorithm is defined to take superpolynomial time if T(n) is not bounded above by any polynomial. Using little omega notation, it is ω(n) time for all constants c, where n is the input parameter, typically the number of bits in the input.

For example, an algorithm that runs for 2 steps on an input of size n requires superpolynomial time (more specifically, exponential time).

An algorithm that uses exponential resources is clearly superpolynomial, but some algorithms are only very weakly superpolynomial. For example, the Adleman–Pomerance–Rumely primality test runs for n time on n-bit inputs; this grows faster than any polynomial for large enough n, but the input size must become impractically large before it cannot be dominated by a polynomial with small degree.

An algorithm that requires superpolynomial time lies outside the complexity class P. Cobham's thesis posits that these algorithms are impractical, and in many cases they are. Since the P versus NP problem is unresolved, it is unknown whether NP-complete problems require superpolynomial time.

Quasi-polynomial time

Quasi-polynomial time algorithms are algorithms whose running time exhibits quasi-polynomial growth, a type of behavior that may be slower than polynomial time but yet is significantly faster than exponential time. The worst case running time of a quasi-polynomial time algorithm is ${\displaystyle 2^{O(\log ^{c}n)}}$ for some fixed ${\displaystyle c>0}$. When ${\displaystyle c=1}$ this gives polynomial time, and for ${\displaystyle c<1}$ it gives sub-linear time.

There are some problems for which we know quasi-polynomial time algorithms, but no polynomial time algorithm is known. Such problems arise in approximation algorithms; a famous example is the directed Steiner tree problem, for which there is a quasi-polynomial time approximation algorithm achieving an approximation factor of ${\displaystyle O(\log ^{3}n)}$ (n being the number of vertices), but showing the existence of such a polynomial time algorithm is an open problem.

Other computational problems with quasi-polynomial time solutions but no known polynomial time solution include the planted clique problem in which the goal is to find a large clique in the union of a clique and a random graph. Although quasi-polynomially solvable, it has been conjectured that the planted clique problem has no polynomial time solution; this planted clique conjecture has been used as a computational hardness assumption to prove the difficulty of several other problems in computational game theory, property testing, and machine learning.

The complexity class QP consists of all problems that have quasi-polynomial time algorithms. It can be defined in terms of DTIME as follows.

${\displaystyle {\mbox{QP}}=\bigcup _{c\in \mathbb {N} }{\mbox{DTIME}}\left(2^{\log ^{c}n}\right)}$

Relation to NP-complete problems

In complexity theory, the unsolved P versus NP problem asks if all problems in NP have polynomial-time algorithms. All the best-known algorithms for NP-complete problems like 3SAT etc. take exponential time. Indeed, it is conjectured for many natural NP-complete problems that they do not have sub-exponential time algorithms. Here "sub-exponential time" is taken to mean the second definition presented below. (On the other hand, many graph problems represented in the natural way by adjacency matrices are solvable in subexponential time simply because the size of the input is the square of the number of vertices.) This conjecture (for the k-SAT problem) is known as the exponential time hypothesis. Since it is conjectured that NP-complete problems do not have quasi-polynomial time algorithms, some inapproximability results in the field of approximation algorithms make the assumption that NP-complete problems do not have quasi-polynomial time algorithms. For example, see the known inapproximability results for the set cover problem.

Sub-exponential time

The term sub-exponential time is used to express that the running time of some algorithm may grow faster than any polynomial but is still significantly smaller than an exponential. In this sense, problems that have sub-exponential time algorithms are somewhat more tractable than those that only have exponential algorithms. The precise definition of "sub-exponential" is not generally agreed upon, however the two most widely used are below.

First definition

A problem is said to be sub-exponential time solvable if it can be solved in running times whose logarithms grow smaller than any given polynomial. More precisely, a problem is in sub-exponential time if for every ε > 0 there exists an algorithm which solves the problem in time O(2). The set of all such problems is the complexity class SUBEXP which can be defined in terms of DTIME as follows.

${\displaystyle {\text{SUBEXP}}=\bigcap _{\varepsilon >0}{\text{DTIME}}\left(2^{n^{\varepsilon }}\right)}$

This notion of sub-exponential is non-uniform in terms of ε in the sense that ε is not part of the input and each ε may have its own algorithm for the problem.

Second definition

Some authors define sub-exponential time as running times in ${\displaystyle 2^{o(n)}}$. This definition allows larger running times than the first definition of sub-exponential time. An example of such a sub-exponential time algorithm is the best-known classical algorithm for integer factorization, the general number field sieve, which runs in time about ${\displaystyle 2^{{\tilde {O}}(n^{1/3})}}$, where the length of the input is n. Another example was the graph isomorphism problem, which the best known algorithm from 1982 to 2016 solved in ${\displaystyle 2^{O\left({\sqrt {n\log n}}\right)}}$. However, at STOC 2016 a quasi-polynomial time algorithm was presented.

It makes a difference whether the algorithm is allowed to be sub-exponential in the size of the instance, the number of vertices, or the number of edges. In parameterized complexity, this difference is made explicit by considering pairs ${\displaystyle (L,k)}$ of decision problems and parameters k. SUBEPT is the class of all parameterized problems that run in time sub-exponential in k and polynomial in the input size n:

${\displaystyle {\text{SUBEPT}}={\text{DTIME}}\left(2^{o(k)}\cdot {\text{poly}}(n)\right).}$

More precisely, SUBEPT is the class of all parameterized problems ${\displaystyle (L,k)}$ for which there is a computable function ${\displaystyle f:\mathbb {N} \to \mathbb {N} }$ with ${\displaystyle f\in o(k)}$ and an algorithm that decides L in time ${\displaystyle 2^{f(k)}\cdot {\text{poly}}(n)}$.

Exponential time hypothesis

The exponential time hypothesis (ETH) is that 3SAT, the satisfiability problem of Boolean formulas in conjunctive normal form with at most three literals per clause and with n variables, cannot be solved in time 2. More precisely, the hypothesis is that there is some absolute constant c > 0 such that 3SAT cannot be decided in time 2 by any deterministic Turing machine. With m denoting the number of clauses, ETH is equivalent to the hypothesis that kSAT cannot be solved in time 2 for any integer k ≥ 3. The exponential time hypothesis implies P ≠ NP.

Exponential time

An algorithm is said to be exponential time, if T(n) is upper bounded by 2, where poly(n) is some polynomial in n. More formally, an algorithm is exponential time if T(n) is bounded by O(2) for some constant k. Problems which admit exponential time algorithms on a deterministic Turing machine form the complexity class known as EXP.

${\displaystyle {\text{EXP}}=\bigcup _{c\in \mathbb {R_{+}} }{\text{DTIME}}\left(2^{n^{c}}\right)}$

Sometimes, exponential time is used to refer to algorithms that have T(n) = 2, where the exponent is at most a linear function of n. This gives rise to the complexity class E.

${\displaystyle {\text{E}}=\bigcup _{c\in \mathbb {N} }{\text{DTIME}}\left(2^{cn}\right)}$

Factorial time

An algorithm is said to be factorial time if T(n) is upper bounded by the factorial function n!. Factorial time is a subset of exponential time (EXP) because ${\displaystyle n!\leq n^{n}=2^{n\log n}=O\left(2^{n^{1+\epsilon }}\right)}$ for all ${\displaystyle \epsilon >0}$. However, it is not a subset of E.

An example of an algorithm that runs in factorial time is bogosort, a notoriously inefficient sorting algorithm based on trial and error. Bogosort sorts a list of n items by repeatedly shuffling the list until it is found to be sorted. In the average case, each pass through the bogosort algorithm will examine one of the n! orderings of the n items. If the items are distinct, only one such ordering is sorted. Bogosort shares patrimony with the infinite monkey theorem.

Double exponential time

An algorithm is said to be double exponential time if T(n) is upper bounded by 2, where poly(n) is some polynomial in n. Such algorithms belong to the complexity class 2-EXPTIME.

${\displaystyle {\mbox{2-EXPTIME}}=\bigcup _{c\in \mathbb {N} }{\mbox{DTIME}}\left(2^{2^{n^{c}}}\right)}$

Well-known double exponential time algorithms include:

• Decision procedures for Presburger arithmetic
• Computing a Gröbner basis (in the worst case)
• Quantifier elimination on real closed fields takes at least double exponential time, and can be done in this time.

See also

• L-notation
• Space complexity

References

1. ^ Sipser, Michael (2006). Introduction to the Theory of Computation. Course Technology Inc. ISBN 0-619-21764-2.
2. Mehlhorn, Kurt; Naher, Stefan (1990). "Bounded ordered dictionaries in O(log log N) time and O(n) space". Information Processing Letters. 35 (4): 183–189. doi:10.1016/0020-0190(90)90022-P.
3. Tao, Terence (2010). "1.11 The AKS primality test". An epsilon of room, II: Pages from year three of a mathematical blog. Graduate Studies in Mathematics. Vol. 117. Providence, RI: American Mathematical Society. pp. 82–86. doi:10.1090/gsm/117. ISBN 978-0-8218-5280-4. MR 2780010.
4. Lenstra, H. W. Jr.; Pomerance, Carl (2019). "Primality testing with Gaussian periods" (PDF). Journal of the European Mathematical Society. 21 (4): 1229–1269. doi:10.4171/JEMS/861. hdl:21.11116/0000-0005-717D-0. MR 3941463. S2CID 127807021.
5. Calude, Cristian S. and Jain, Sanjay and Khoussainov, Bakhadyr and Li, Wei and Stephan, Frank (2017). "Deciding parity games in quasipolynomial time". Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing. Association for Computing Machinery. pp. 252–263. doi:10.1145/3055399.3055409. hdl:2292/31757. ISBN 9781450345286. S2CID 30338402.{{cite book}}: CS1 maint: multiple names: authors list (link)
6. ^ Babai, László; Fortnow, Lance; Nisan, N.; Wigderson, Avi (1993). "BPP has subexponential time simulations unless EXPTIME has publishable proofs". Computational Complexity. 3 (4). Berlin, New York: Springer-Verlag: 307–318. doi:10.1007/BF01275486. S2CID 14802332.
7. Bradford, Phillip G.; Rawlins, Gregory J. E.; Shannon, Gregory E. (1998). "Efficient matrix chain ordering in polylog time". SIAM Journal on Computing. 27 (2): 466–490. doi:10.1137/S0097539794270698. MR 1616556.
8. Holm, Jacob; Rotenberg, Eva (2020). "Fully-dynamic planarity testing in polylogarithmic time". In Makarychev, Konstantin; Makarychev, Yury; Tulsiani, Madhur; Kamath, Gautam; Chuzhoy, Julia (eds.). Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing, STOC 2020, Chicago, IL, USA, June 22-26, 2020. Association for Computing Machinery. pp. 167–180. arXiv:1911.03449. doi:10.1145/3357713.3384249. ISBN 978-1-4503-6979-4.
9. Kumar, Ravi; Rubinfeld, Ronitt (2003). "Sublinear time algorithms" (PDF). SIGACT News. 34 (4): 57–67. doi:10.1145/954092.954103. S2CID 65359.
10. Rubinfeld, Ronitt (2019). "Local Computation Algorithms". Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing (PODC). p. 3. doi:10.1145/3293611.3331587. ISBN 978-1-4503-6217-7.
11. Naik, Ashish V.; Regan, Kenneth W.; Sivakumar, D. (1995). "On quasilinear-time complexity theory" (PDF). Theoretical Computer Science. 148 (2): 325–349. doi:10.1016/0304-3975(95)00031-Q. MR 1355592.
12. Sedgewick, Robert; Wayne, Kevin (2011). Algorithms (4th ed.). Pearson Education. p. 186.
13. Papadimitriou, Christos H. (1994). Computational complexity. Reading, Mass.: Addison-Wesley. ISBN 0-201-53082-1.
14. Cobham, Alan (1965). "The intrinsic computational difficulty of functions". Proc. Logic, Methodology, and Philosophy of Science II. North Holland.
15. Braverman, Mark; Kun-Ko, Young; Rubinstein, Aviad; Weinstein, Omri (2017). "ETH hardness for densest-k-subgraph with perfect completeness". In Klein, Philip N. (ed.). Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2017, Barcelona, Spain, Hotel Porta Fira, January 16-19. Society for Industrial and Applied Mathematics. pp. 1326–1341. arXiv:1504.08352. doi:10.1137/1.9781611974782.86. ISBN 978-1-61197-478-2. MR 3627815.
16. Complexity Zoo: Class QP: Quasipolynomial-Time
17. ^ Impagliazzo, Russell; Paturi, Ramamohan (2001). "On the complexity of k-SAT" (PDF). Journal of Computer and System Sciences. 62 (2): 367–375. doi:10.1006/jcss.2000.1727. MR 1820597.
18. Aaronson, Scott (5 April 2009). "A not-quite-exponential dilemma". Shtetl-Optimized. Retrieved 2 December 2009.
19. Complexity Zoo: Class SUBEXP: Deterministic Subexponential-Time
20. Moser, P. (2003). "Baire's Categories on Small Complexity Classes". In Andrzej Lingas; Bengt J. Nilsson (eds.). Fundamentals of Computation Theory: 14th International Symposium, FCT 2003, Malmö, Sweden, August 12-15, 2003, Proceedings. Lecture Notes in Computer Science. Vol. 2751. Berlin, New York: Springer-Verlag. pp. 333–342. doi:10.1007/978-3-540-45077-1_31. ISBN 978-3-540-40543-6. ISSN 0302-9743.
21. Miltersen, P.B. (2001). "Derandomizing Complexity Classes". Handbook of Randomized Computing. Combinatorial Optimization. 9. Kluwer Academic Pub: 843. doi:10.1007/978-1-4615-0013-1_19 (inactive 1 November 2024). ISBN 978-1-4613-4886-3.{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link)
22. Kuperberg, Greg (2005). "A Subexponential-Time Quantum Algorithm for the Dihedral Hidden Subgroup Problem". SIAM Journal on Computing. 35 (1). Philadelphia: 188. arXiv:quant-ph/0302112. doi:10.1137/s0097539703436345. ISSN 1095-7111. S2CID 15965140.
23. Oded Regev (2004). "A Subexponential Time Algorithm for the Dihedral Hidden Subgroup Problem with Polynomial Space". arXiv:quant-ph/0406151v1.
24. Grohe, Martin; Neuen, Daniel (2021). "Recent advances on the graph isomorphism problem". In Dabrowski, Konrad K.; Gadouleau, Maximilien; Georgiou, Nicholas; Johnson, Matthew; Mertzios, George B.; Paulusma, Daniël (eds.). Surveys in combinatorics 2021. London Mathematical Society Lecture Note Series. Vol. 470. Cambridge University Press. pp. 187–234. arXiv:2011.01366. ISBN 978-1-009-01888-3. MR 4273431.
25. Flum, Jörg; Grohe, Martin (2006). Parameterized Complexity Theory. Springer. p. 417. ISBN 978-3-540-29952-3.
26. Impagliazzo, R.; Paturi, R.; Zane, F. (2001). "Which problems have strongly exponential complexity?". Journal of Computer and System Sciences. 63 (4): 512–530. doi:10.1006/jcss.2001.1774.
27. Mayr, Ernst W.; Meyer, Albert R. (1982). "The complexity of the word problems for commutative semigroups and polynomial ideals". Advances in Mathematics. 46 (3): 305–329. doi:10.1016/0001-8708(82)90048-2. hdl:1721.1/149010. MR 0683204.
28. Davenport, James H.; Heintz, Joos (1988). "Real quantifier elimination is doubly exponential". Journal of Symbolic Computation. 5 (1–2): 29–35. doi:10.1016/S0747-7171(88)80004-X. MR 0949111.
29. Collins, George E. (1975). "Quantifier elimination for real closed fields by cylindrical algebraic decomposition". In Brakhage, H. (ed.). Automata Theory and Formal Languages: 2nd GI Conference, Kaiserslautern, May 20–23, 1975. Lecture Notes in Computer Science. Vol. 33. Springer. pp. 134–183. doi:10.1007/3-540-07407-4_17. ISBN 978-3-540-07407-6. MR 0403962.

• Analysis of algorithms
• Computational complexity theory
• Computational resources
• Time