Misplaced Pages

Talk:Real projective line: Difference between revisions

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Browse history interactively← Previous editContent deleted Content addedVisualWikitext
Revision as of 17:27, 23 June 2015 editTkuvho (talk | contribs)Autopatrolled, Pending changes reviewers, Rollbackers9,424 edits →Mathematics made difficult← Previous edit Latest revision as of 11:29, 1 December 2024 edit undoD.Lazard (talk | contribs)Extended confirmed users33,863 edits →Is image correct?: ReplyTag: Reply 
(72 intermediate revisions by 16 users not shown)
Line 1: Line 1:
{{WikiProject banner shell|class=B|
==New start==
{{WikiProject Mathematics|importance=high}}
Here is my contribution for a dedicated article: "Real projective line".] (]) 20:55, 21 June 2015 (UTC)
}}
:Thanks for great work! ] (]) 07:32, 22 June 2015 (UTC)
{{archives}}
__TOC__


== The main image with the circle ==
== non-desarguean? ==


The main image looks something like a circle with one point representing both negative and positive infinity. I find this image confusing. I picture the real projective line as a real line with two added points, Inf and -Inf. An even better picture in my mind I get is just the real number line and two added dots. Is this image misleading or not? I don't have any reference texts beside me to cite at the moment, sorry. ] (]) 00:19, 26 January 2016 (UTC)
The current version contains the footnote "If a real projective line happens to appear in a non-Desarguesian plane the harmonic structure cannot be presumed." Now the usual embedding of this would be in the real projective plane, rather than some other non-Desarguean plane. This is certainly possible for example by using the projective plane over the Cayley numbers. However, I am wondering about the relevance of this footnote at this page. ] (]) 07:32, 22 June 2015 (UTC)


:There is only one point at infinity on the projective line. You're perhaps thinking of the ]. <small><span style="display:inline-block;vertical-align:-.3em;line-height:.8em;text-align:right;text-shadow:black 1pt 1pt 1pt">]<br/>]</span></small> 01:07, 26 January 2016 (UTC)
:The embedding in a non-Desarguesian plane is but one possibility. If the usual axioms are applied to the line with no embedding, the group of motions can be considerably larger. So if the article is to mention the non-Desarguesian direction, this requires a more thorough covering the possibilities. —] 13:24, 22 June 2015 (UTC)
::The embedding of a real projective line in a non-Desarguean plane has no projective meaning, strictly speaking. Of course in differential geometry it does, but it is not the subject of this page. ] (]) 14:37, 22 June 2015 (UTC)
:::I agree, that kind of embedding is not natural and mentioning non-Desarguesian planes seems quite out of place in this article. ] (]) 17:39, 22 June 2015 (UTC)


:: Ah, alright. thanks. I got them confused for a second. Why is there a circle. Sorry, still haven't gotten any reference texts. I'm too lazy to walk upstairs and check out the needed books, lmao. ] (]) 02:20, 26 January 2016 (UTC)
== Construction over the ]: can't be glossed over ==


== redundant articles ==
The construction over the ], recently added, needs considerable work. One cannot simply add a point to the real line as defined in that article and get the real projective line as a geometric object. That article gives a hopelessly unclearly defined object for the purpose. One needs to start specifically with the real affine line, a homogeneous space, whereas it is difficult, from that article, to think, geometrically, of anything other than an object of which the group of automorphisms is the trivial group. Secondly, even starting with a one-dimensional affine real space (also not Euclidean: it must have no metric structure), one has to include a construction for changing the added point into a normal point, i.e. expanding the group of motions in a particular way. So, placing this as the first alternative of a definition for the construction implies far too much assumption; this needs to be fixed. For now, I'd suggest removing this until a full section explaining the construction correctly can be added. —] 13:44, 22 June 2015 (UTC)
:The only problem is that all of the theorems of projective geometry such as Pappus, Desargues, Pascal, etc. become inapplicable to affine configurations if one does not include a mention of the construction via adding points at infinity, which is a considerable loss if one is interested in actual applications of projective geometry :-) Metric structures are irrelevant here. ] (]) 14:39, 22 June 2015 (UTC)
::Perhaps thinking of the construction of the real projective line as the set of all lines through the origin in {{math|'''R'''<sup>2</sup>}} would be fruitful. Identifying these lines with their slopes gives the real line and the vertical line through the origin gives the point at infinity. The homogeneous nature of the result is quite apparent from this viewpoint. The non-uniqueness of the coordinatization (or embedding, if you prefer) can also be made very clear. ] (]) 17:34, 22 June 2015 (UTC)
::This view of the construction also shows that the first sentence in the definition section is not really correct. I would also advocate putting in a mention of the point at infinity, but this has to be done carefully. One should not start with the real line and think of adding a point to it, as this gets you into the difficulties that {{u|Quondum}} has mentioned (not insurmountable, but it requires some work to get it right). Rather, start with the real projective line and point out that the removal of one point leaves you with a copy of the real line and the removed point can be thought of as the "point at infinity" with respect to that copy. ] (]) 16:56, 23 June 2015 (UTC)


There are articles on ] and ] that overlap severely with this one. The first could probably be eliminated and seems to be a WP:FORK. Possibly merge all three. ] (]) 23:18, 15 June 2020 (UTC)
== Day-one review ==
:It is true that '''the''' ] is '''a''' ], but the converse is wrong. In particular, the projectively extended real line is a ], which real projective lines are generally not. In particular, there is an arithmetic on the projectively extended real line (<math>1/0=\infty</math>) that does not extend to other real projective lines. So, these two articles are about two related topics, none being a subtopic of the other. Moreover, the intended audience of these two article is completely different. So, there is no reason for merging them.
:On the other hand, the only part of ] that is specific to the real case, is the ] structure (one single section). So, I would not oppose to a merge with ], if the merged article remains accessible for readers who know real numbers but not general fields. ] (]) 07:18, 16 June 2020 (UTC)
:: That article on "a" ] uses the "a" form in the first paragraph only (2 times) and "the real projective line" in the rest of the article (16 times).


:: You seem to be speaking of a canonized P^1(R) ("the" proj line, qua number system) that non-canonically coordinatizes all other lines ("a" line) in projective geometry. If so then the names should match the same dichotomy in the non-projective case: ] system and ] versus geometric ] in real (Euclidean, affine, or vector) space. The analogue would be "projectivized (real) numbers" or "projective (real) number line" for the coordinate system and ] in projective geometry (or projective extension of affine lines).
Good participation for mid-summer. All comments directed to improved article with clear experience in bringing this topic out for general review. Some changes were made this afternoon reflecting discussion in the last 24 hours, including a link to ] showing that it is relative to chart selection. Please add to the See also as appropriate; my contribution is ]. This subtle little object from an old geometrical practice has an important place in math, we do well to explicate it clearly. As for the non-Desarguesian situation, that technicality that Hilbert and others used to upset expectations of old, it is mentioned as a caveat since it may arise in advanced studies.] (]) 23:25, 22 June 2015 (UTC)


:: P^1 as a number system is questionable. Does anyone refer to it as such? I have never heard any extension of rational functions to the one-point compactification described as a calculation in P^1 considered as an algebraic structure or a number system. P^1 is in such cases considered as an extension of the domain or range of the function, not as an expansion of the number system. ] (]) 06:55, 17 June 2020 (UTC)
== ] ==


== There is a natural left action of {{math|PGL<sub>2</sub>('''R''')}} on {{math|'''P'''<sup>1</sup>('''R''')}} ==
This is probably the most complicated way I have ever seen to describe a circle. The lede says that the thing is homeomorphic to a circle, seemingly implying that it has a different geometric structure, and then gratuitously mentions that it is a non-trivial smooth manifold. Actually, though, the natural distance function on any real projective space is simply the angle between lines, which can be up to <math>\frac{\pi}{2}</math>. In this case, this is the same as the metric of a circle. So it's not just homeomorphic to a circle, it ''is'' a circle, specifically a circle of radius <math>\frac{1}{2}</math>. Will anybody mind if I simplify the lede accordingly? Also the construction itself is a little technical and is not intuitively explained - it should be stated explicitly that the points of <math>\mathbb{R}P^{1}</math> are lines in <math>\mathbb{R}^2</math> passing through the origin. And we should definitely mention that it is commonly understood as the one-point compactification of the real line; even though, as ] notes, this does make it a little less clear what the metric is, we can do away with this problem by mentioning that the metric is that of the circle. (A little more technically, the Riemannian metric of the real-line-with-point-at-infinity model of <math>\mathbb{R}P^{1}</math> is <math>\frac{dx}{1+x^2}</math>, which is obtained by pushing forward the Euclidean metric <math>dx</math> by <math>\arctan</math>, the obvious map which takes points on the real line to angles.)


The group {{math|GL<sub>2</sub>('''R''')}} acts on the left on the space of column vectors {{math|'''R'''<sup>2</sup>}} by matrix multiplication. In this way, each matrix ''A'' defines a function {{math|''f''<sub>''A''</sub>}} from {{math|'''R'''<sup>2</sup>}} to {{math|'''R'''<sup>2</sup>}}. If ''B'' is another matrix, then <math>f_A \circ f_B = f_{AB}</math> because <math>f_A(f_B(v)) = f_A(Bv)=A(Bv) = (AB)v = f_{AB}(v)</math> holds for all column vectors <math>v \in \mathbf{R}^2</math>. Thus matrix multiplication is compatible with composition, when one uses the left action on column vectors. The same then follows for the induced left action of {{math|PGL<sub>2</sub>('''R''')}} on {{math|'''P'''<sup>1</sup>('''R''')}}.
In the "automorphisms" section, it doesn't quite make sense to say "the mappings are homographies" - what we really mean is that the homographies are mappings of special interest. We also should probably mention that <math>PGL_{2}(\mathbb{R})</math> is the isometry group of the hyperbolic plane, which in the Poincare disc model can be seen as the interior of the circle. The real projective line then can be seen as imbedded in the complex projective line, and this explains the statement that the group of homographies is intermediate between the modular group and the full Moebius group. Does anybody mind if I make these changes as well?


Indeed, it is this left action on {{math|'''P'''<sup>1</sup>('''R''')}}, with <math>\begin{pmatrix} a&b\\c&d \end{pmatrix}</math> acting as <math>x \mapsto (ax+b)/(cx+d)</math>, that one finds in standard references such as
I think the "Structure" section might do with some expansion - I really don't understand what it says and I'm not familiar with all that classical geometry stuff. --] (]) 05:58, 23 June 2015 (UTC)
* Serre, A course in arithmetic, VII.1.1.
* Miyake, Modular forms, §1.1.
* Lang, Complex analysis, VII, §5.
* Lang, Elliptic functions, 3.§1.
* Stillwell, Mathematics and its history, §8.6.
* Koblitz, Introduction to elliptic curves and modular forms, III.§1.
(Some of these references are over '''C''', but the principle is the same over every field.)


If anyone disagrees with all these authors, can you please explain why and list the published references you are using to support your claim? Thank you, ] (]) 04:59, 27 December 2020 (UTC)
:This comment expresses some legitimate concerns. There is one point I don't follow. It is true that the homographies are isometries of the hyperbolic plane, but why do you write "the real projective line then can be seen as imbedded in the complex projective line"? The imbedding in the complex projective line is merely the extension of coefficients, and needs not be explained in terms of hyperbolic isometries. ] (]) 07:35, 23 June 2015 (UTC)


:Due to the ] involution, the group PSL(R) can also be presented as the ] given in the "left action". Practicing geometers like ] and ] use ]s and right action. Look at all the parentheses necessary in the presentation of the opposite group! The carry-over of prefix notation for functions, used in calculus and complex analysis, lets some authors (as listed) use the confusing reverse writing, but this article is about geometry and transformation. The composed transformation AB in a group is usually read in the order written; the "left action" expects B to be applied to the column vector before A is applied, clearly corresponding to the group opposite to what geometers such as Hirschfeld & Artzy prefer. Some readers may need to refer to the contribution of December 27, 2020, about PSL(R) that has been changed. — ] (]) 03:10, 30 December 2020 (UTC)
::I guess that the homographies of the real projective line may be related to the motions of the omega points of the hyperbolic plane; this would explain the group being the same and may be worth a mention. This seems far more natural (or at least more intuitive) to me than the relationship with the complex projective line; Tkuvho's argument around on complexification makes sense. —] 14:53, 23 June 2015 (UTC)


Thank you for your response! I have heard that several decades ago, there was a pocket of mathematicians in the U.K. who started writing functions to the right of their arguments, so that to apply the composition f∘g one would apply f first and g second, as you mention. But it was a losing battle, and I think that essentially all of them abandoned that notation. Even ], it seems, now writes his transformations on projective space using matrices acting on the left: see p. 4 of his 2008 book ''Algebraic curves over a finite field''. And ] seems to have passed away in 2006, so one can hardly call him a practicing geometer.
:::Well the idea is that you take <math>\mathbb{C}^2</math> and form the complex projective line, and look at what happened to the plane spanned by the two real axes: it became a real projective line which is the boundary of the upper half-plane <math>H^{2}</math>. The homographies of this line are precisely the Moebius transformations which fix it - these are the linear fractional transformations with real coefficients; they are also the isometries of <math>H^{2}</math>. This explains the relationship mentioned in the text, that the modular group (a group of hyperbolic isometries) is a subgroup of the group of homographies of <math>\mathbb{R}P^1</math>, which is in turn a subgroup of the Moebius group. --] (]) 16:20, 23 June 2015 (UTC)

::::There is no connection whatsoever in what you describe between the representation of the real projective line as a subset of the complex projective line, on the one hand, and its representation as the "boundary" of the hyperbolic plane, on the other. ] (]) 16:24, 23 June 2015 (UTC)
Writing functions to the left of their arguments is the standard in virtually all of mathematics, not just calculus and complex analysis, and this includes almost all branches of geometry as well. The vast majority of users of the projective line will be more familiar with this standard convention. If you still feel it is worth mentioning that there is a convention in which transformations are written on the right, this could be done in a note with a citation to a book that uses this convention, but I feel that it would be wrong to present this convention in the main text as if it were standard in the 21st century.
:::::Of course there is - the hyperbolic plane (half-plane model) is half of the Riemann sphere a.k.a. <math>\mathbb{C}P^1</math>, and the <math>\mathbb{R}P^1</math> constructed as above is the boundary of it. It's not a coincidence that the Moebius transformations (complex homographies) which fix <math>H^{2}</math> (or equivalently which fix <math>\partial H^{2}</math>) are precisely the hyperbolic isometries. This occurs because the Moebius transformations are the conformal bijections which map circles to circles, and the geodesics of <math>H^{2}</math> are circles which intersect the boundary orthogonally, so a transformation will be an isometry of <math>H^{2}</math> iff it fixes <math>\partial H^{2}</math>, maps circles to circles, and preserves angles. --] (]) 16:56, 23 June 2015 (UTC)

::::::This is a misleading point of view. The complex homographies in general don't fix the real projective line, and form a much larger group, namely PSL(2,C), than the real homographies. Not much is gained by viewing the hyperbolic plane as "half" the complex projective line. ] (]) 17:06, 23 June 2015 (UTC)
By the way, by PSL(R) do you mean {{math|1= PSL<sub>2</sub>('''R''') = SL<sub>2</sub>('''R''')/{±1}}}? That group is not the full group of linear automorphisms of {{math|'''P'''<sup>1</sup>('''R''')}}. ] (]) 04:50, 30 December 2020 (UTC)
:::::::Right, so the point is that those elements of <math>PSL_{2} (\mathbb{C})</math> which do fix the real line are the real homographies. This is the way to find out that the isometry group of the hyperbolic plane is <math>PSL_{2} (\mathbb{R})</math> - I don't know of another way to prove this, offhand. It's also the view universally taken in the study of Riemann surfaces and analytic number theory. --] (]) 17:19, 23 June 2015 (UTC)

::::::::But the hyperbolic metric has little to do with this, and it certainly cannot be induced by the imbedding into the complex projective line, so in a way using the phrase "hyperbolic plane" in relation to the complex projective line is neither here nor there. Fractional linear transformations act in the upperhalf plane and give all the isometries, so one doesn't need to ever speak of projective geometry to understand basic facts about the hyperbolic group of isometries. Of course the crossratio provides a nice way of defining the hyperbolic metric. ] (]) 17:26, 23 June 2015 (UTC)
:Functions are a type of ]. The representation of functions in the ] puts some context to this discussion. In particular, ] turns the tables on the prefix notation, making it the out-dated scheme. Some practice in this more general context leads to an appreciation of the clarity provided by right action. — ] (]) 05:25, 31 December 2020 (UTC)
::Almost all mathematics is built up on the convention that in a composition of functions,<math>f\circ g,</math> the function {{mvar|g}} is applied first, that is, <math>(f\circ g)(x)=f(g(x)).</math> It is for complying with this convention that the matrix multiplication is defined by combining rows of the first matrix with columns of the second matrix, and that the matrix representation of a ] is a column matrix. Historically, these conventions, and several others, took some time for being elaborated in a coherent way. An example of survival of older conventions is ], where the Sylvester matrix is written as the transpose of the matrix of the corresponding linear map. It is possible to choose the opposite convention, but coherency would imply to change all related conventions, and therefore to change accordingly almost all mathematical articles. It is certainly not the role of Misplaced Pages to promote such a dramatic change.
::It is possible that in some specific areas of mathematics (possibly the theory of relations), with few interaction with the main stream of mathematics, it is convenient to use a different conversion. But, for being usable in other areas of mathematics, the theorems obtained in such an area (if any) must be translated in the standard convention.
::For this reason, {{u|Rgdboer}}'s version is not acceptable, and {{u|Ebony Jackson}}'s must be kept. However, a confusing point must be clarified, which is the implicit use of <math></math> as a column matrix. I believe that this is the hidden origin of this discussion, and I'll try to clarify this in the article. ] (]) 10:57, 31 December 2020 (UTC)
:To clarify the choice, see ] recently contributed. — ] (]) 04:29, 3 January 2021 (UTC)

== Is image correct? ==

]

I tried to find a formula that gives me value for any provided angle. It is a piecewise function that is defined as:<br>
<math>f(x)= \begin{cases}\frac{\pi}{-2\pi-2x}, & x \in (-\pi,-1] \\\frac{2x}{\pi}, & x \in (-1, 1) \\\frac{\pi}{2\pi-2x}, & x \in [1, \pi)\end{cases}</math> <br>
So I have two questions. <br>
1. Do values near dots on a picture represent actual values or are numbers not attached to a particular place and persist only for illustrative purposes?<br>
2. If values are attached to particular places, should they be represented by that formula? ] (]) 15:45, 22 November 2024 (UTC)

:The diagram is supposed to be only illustrative. If you want an exact transformation, you should use the ] (as a one-dimensional function of angle measure, the "half-tangent"). Then 1/2 and 2 will be about 53.1° and 126.9° away from 0, respectively, compared to 1 being 90° away from 0. The appropriate function is: <math display=block>f(x) = \tan\tfrac12x.</math> –] ] 23:09, 22 November 2024 (UTC)
:Thanks. I thought about tangent as natural way to fit infinite numbers into some range but that one on the picture has very interesting symmetries. I want to know more about that, but looks like it is just illustration without any deep meaning ] (]) 22:49, 23 November 2024 (UTC)
]
Given that a projective space is formed by identifying antipodal points in a sphere of a Euclidean space of one higher dimension, the semicircle is the natural picture for the real projective line. — ] (]) 02:40, 1 December 2024 (UTC)

:I find this image misleading. Indeed, in a projective line, all points play the same role, which is the case in the full circle representation, but not in the semicircle model. ] (]) 11:29, 1 December 2024 (UTC)

Latest revision as of 11:29, 1 December 2024

This article is rated B-class on Misplaced Pages's content assessment scale.
It is of interest to the following WikiProjects:
WikiProject iconMathematics High‑priority
WikiProject iconThis article is within the scope of WikiProject Mathematics, a collaborative effort to improve the coverage of mathematics on Misplaced Pages. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.MathematicsWikipedia:WikiProject MathematicsTemplate:WikiProject Mathematicsmathematics
HighThis article has been rated as High-priority on the project's priority scale.
Archiving icon
Archives
Archive 1

The main image with the circle

The main image looks something like a circle with one point representing both negative and positive infinity. I find this image confusing. I picture the real projective line as a real line with two added points, Inf and -Inf. An even better picture in my mind I get is just the real number line and two added dots. Is this image misleading or not? I don't have any reference texts beside me to cite at the moment, sorry. 137.124.161.17 (talk) 00:19, 26 January 2016 (UTC)

There is only one point at infinity on the projective line. You're perhaps thinking of the extended real line. Sławomir
Biały 01:07, 26 January 2016 (UTC)
Ah, alright. thanks. I got them confused for a second. Why is there a circle. Sorry, still haven't gotten any reference texts. I'm too lazy to walk upstairs and check out the needed books, lmao. 137.124.161.17 (talk) 02:20, 26 January 2016 (UTC)

redundant articles

There are articles on projectively extended real line and projective line that overlap severely with this one. The first could probably be eliminated and seems to be a WP:FORK. Possibly merge all three. 73.89.25.252 (talk) 23:18, 15 June 2020 (UTC)

It is true that the projectively extended real line is a real projective line, but the converse is wrong. In particular, the projectively extended real line is a number system, which real projective lines are generally not. In particular, there is an arithmetic on the projectively extended real line ( 1 / 0 = ∞ {\displaystyle 1/0=\infty } ) that does not extend to other real projective lines. So, these two articles are about two related topics, none being a subtopic of the other. Moreover, the intended audience of these two article is completely different. So, there is no reason for merging them.
On the other hand, the only part of Real projective line that is specific to the real case, is the manifold structure (one single section). So, I would not oppose to a merge with Projective line, if the merged article remains accessible for readers who know real numbers but not general fields. D.Lazard (talk) 07:18, 16 June 2020 (UTC)
That article on "a" real projective line uses the "a" form in the first paragraph only (2 times) and "the real projective line" in the rest of the article (16 times).
You seem to be speaking of a canonized P^1(R) ("the" proj line, qua number system) that non-canonically coordinatizes all other lines ("a" line) in projective geometry. If so then the names should match the same dichotomy in the non-projective case: real number system and real number line versus geometric lines in real (Euclidean, affine, or vector) space. The analogue would be "projectivized (real) numbers" or "projective (real) number line" for the coordinate system and lines in projective geometry (or projective extension of affine lines).
P^1 as a number system is questionable. Does anyone refer to it as such? I have never heard any extension of rational functions to the one-point compactification described as a calculation in P^1 considered as an algebraic structure or a number system. P^1 is in such cases considered as an extension of the domain or range of the function, not as an expansion of the number system. 73.89.25.252 (talk) 06:55, 17 June 2020 (UTC)

There is a natural left action of PGL2(R) on P(R)

The group GL2(R) acts on the left on the space of column vectors R by matrix multiplication. In this way, each matrix A defines a function fA from R to R. If B is another matrix, then f A ∘ f B = f A B {\displaystyle f_{A}\circ f_{B}=f_{AB}} because f A ( f B ( v ) ) = f A ( B v ) = A ( B v ) = ( A B ) v = f A B ( v ) {\displaystyle f_{A}(f_{B}(v))=f_{A}(Bv)=A(Bv)=(AB)v=f_{AB}(v)} holds for all column vectors v ∈ R 2 {\displaystyle v\in \mathbf {R} ^{2}} . Thus matrix multiplication is compatible with composition, when one uses the left action on column vectors. The same then follows for the induced left action of PGL2(R) on P(R).

Indeed, it is this left action on P(R), with ( a b c d ) {\displaystyle {\begin{pmatrix}a&b\\c&d\end{pmatrix}}} acting as x ↦ ( a x + b ) / ( c x + d ) {\displaystyle x\mapsto (ax+b)/(cx+d)} , that one finds in standard references such as

  • Serre, A course in arithmetic, VII.1.1.
  • Miyake, Modular forms, §1.1.
  • Lang, Complex analysis, VII, §5.
  • Lang, Elliptic functions, 3.§1.
  • Stillwell, Mathematics and its history, §8.6.
  • Koblitz, Introduction to elliptic curves and modular forms, III.§1.

(Some of these references are over C, but the principle is the same over every field.)

If anyone disagrees with all these authors, can you please explain why and list the published references you are using to support your claim? Thank you, Ebony Jackson (talk) 04:59, 27 December 2020 (UTC)

Due to the transpose involution, the group PSL(R) can also be presented as the opposite group given in the "left action". Practicing geometers like J. W. P. Hirschfeld and Rafael Artzy use row vectors and right action. Look at all the parentheses necessary in the presentation of the opposite group! The carry-over of prefix notation for functions, used in calculus and complex analysis, lets some authors (as listed) use the confusing reverse writing, but this article is about geometry and transformation. The composed transformation AB in a group is usually read in the order written; the "left action" expects B to be applied to the column vector before A is applied, clearly corresponding to the group opposite to what geometers such as Hirschfeld & Artzy prefer. Some readers may need to refer to the contribution of December 27, 2020, about PSL(R) that has been changed. — Rgdboer (talk) 03:10, 30 December 2020 (UTC)

Thank you for your response! I have heard that several decades ago, there was a pocket of mathematicians in the U.K. who started writing functions to the right of their arguments, so that to apply the composition f∘g one would apply f first and g second, as you mention. But it was a losing battle, and I think that essentially all of them abandoned that notation. Even J. W. P. Hirschfeld, it seems, now writes his transformations on projective space using matrices acting on the left: see p. 4 of his 2008 book Algebraic curves over a finite field. And Rafael Artzy seems to have passed away in 2006, so one can hardly call him a practicing geometer.

Writing functions to the left of their arguments is the standard in virtually all of mathematics, not just calculus and complex analysis, and this includes almost all branches of geometry as well. The vast majority of users of the projective line will be more familiar with this standard convention. If you still feel it is worth mentioning that there is a convention in which transformations are written on the right, this could be done in a note with a citation to a book that uses this convention, but I feel that it would be wrong to present this convention in the main text as if it were standard in the 21st century.

By the way, by PSL(R) do you mean PSL2(R) = SL2(R)/{±1}? That group is not the full group of linear automorphisms of P(R). Ebony Jackson (talk) 04:50, 30 December 2020 (UTC)

Functions are a type of binary relation. The representation of functions in the calculus of relations puts some context to this discussion. In particular, composition of relations turns the tables on the prefix notation, making it the out-dated scheme. Some practice in this more general context leads to an appreciation of the clarity provided by right action. — Rgdboer (talk) 05:25, 31 December 2020 (UTC)
Almost all mathematics is built up on the convention that in a composition of functions, f ∘ g , {\displaystyle f\circ g,} the function g is applied first, that is, ( f ∘ g ) ( x ) = f ( g ( x ) ) . {\displaystyle (f\circ g)(x)=f(g(x)).} It is for complying with this convention that the matrix multiplication is defined by combining rows of the first matrix with columns of the second matrix, and that the matrix representation of a coordinate vector is a column matrix. Historically, these conventions, and several others, took some time for being elaborated in a coherent way. An example of survival of older conventions is Sylvester matrix, where the Sylvester matrix is written as the transpose of the matrix of the corresponding linear map. It is possible to choose the opposite convention, but coherency would imply to change all related conventions, and therefore to change accordingly almost all mathematical articles. It is certainly not the role of Misplaced Pages to promote such a dramatic change.
It is possible that in some specific areas of mathematics (possibly the theory of relations), with few interaction with the main stream of mathematics, it is convenient to use a different conversion. But, for being usable in other areas of mathematics, the theorems obtained in such an area (if any) must be translated in the standard convention.
For this reason, Rgdboer's version is not acceptable, and Ebony Jackson's must be kept. However, a confusing point must be clarified, which is the implicit use of [ x : y ] {\displaystyle } as a column matrix. I believe that this is the hidden origin of this discussion, and I'll try to clarify this in the article. D.Lazard (talk) 10:57, 31 December 2020 (UTC)
To clarify the choice, see Geometric transformation#Opposite group actions recently contributed. — Rgdboer (talk) 04:29, 3 January 2021 (UTC)

Is image correct?

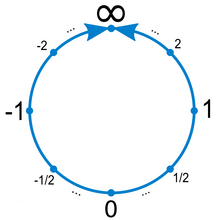
I tried to find a formula that gives me value for any provided angle. It is a piecewise function that is defined as:
f ( x ) = { π − 2 π − 2 x , x ∈ ( − π , − 1 ] 2 x π , x ∈ ( − 1 , 1 ) π 2 π − 2 x , x ∈ [ 1 , π ) {\displaystyle f(x)={\begin{cases}{\frac {\pi }{-2\pi -2x}},&x\in (-\pi ,-1]\\{\frac {2x}{\pi }},&x\in (-1,1)\\{\frac {\pi }{2\pi -2x}},&x\in [1,\pi )\end{cases}}}
So I have two questions.
1. Do values near dots on a picture represent actual values or are numbers not attached to a particular place and persist only for illustrative purposes?
2. If values are attached to particular places, should they be represented by that formula? Отец Никифор (talk) 15:45, 22 November 2024 (UTC)

The diagram is supposed to be only illustrative. If you want an exact transformation, you should use the stereographic projection (as a one-dimensional function of angle measure, the "half-tangent"). Then 1/2 and 2 will be about 53.1° and 126.9° away from 0, respectively, compared to 1 being 90° away from 0. The appropriate function is: f ( x ) = tan ⁡ 1 2 x . {\displaystyle f(x)=\tan {\tfrac {1}{2}}x.} –jacobolus (t) 23:09, 22 November 2024 (UTC)
Thanks. I thought about tangent as natural way to fit infinite numbers into some range but that one on the picture has very interesting symmetries. I want to know more about that, but looks like it is just illustration without any deep meaning Отец Никифор (talk) 22:49, 23 November 2024 (UTC)
Semicircle model of the real projective line

Given that a projective space is formed by identifying antipodal points in a sphere of a Euclidean space of one higher dimension, the semicircle is the natural picture for the real projective line. — Rgdboer (talk) 02:40, 1 December 2024 (UTC)

I find this image misleading. Indeed, in a projective line, all points play the same role, which is the case in the full circle representation, but not in the semicircle model. D.Lazard (talk) 11:29, 1 December 2024 (UTC)
Categories: