| Revision as of 20:00, 23 July 2024 view sourceJacobolus (talk | contribs)Extended confirmed users35,739 editsm Undid revision 1236192506 by Shashvat Verma (talk) – we have essentially no convincing evidence about whether Thales was or wasn't a mathematician. this is discussed in the articleTag: Undo← Previous edit | Revision as of 20:02, 23 July 2024 view source Jacobolus (talk | contribs)Extended confirmed users35,739 editsm →Mathematics: give an inline approximate date to HieronymusNext edit → | ||
| Line 105: | Line 105: | ||
| Thales was known for introducing the theoretical and practical use of ] to Greece, and has been described as the first person in the western world to apply deductive reasoning to geometry, making him the West's "first mathematician."<ref name="books.google.com" /><ref>{{Harvnb|Boyer|1989|p=43 (3rd ed.)|edition=3rd}}</ref><ref name="gazette">{{cite journal |last=Fletcher |first=Colin R. |date=December 1982 |title=Thales – our founder? |journal=The Mathematical Gazette |volume=66 |issue=438 |page=267 |doi=10.2307/3615512 |jstor=3615512 |s2cid=125626522}}</ref> He is also credited with the West's oldest definition of ]: a "collection of units", "following the Egyptian view".<ref>{{Cite web |url=https://books.google.com/books?id=wdhMAAAAMAAJ |title=Introduction to Arithmetic|last=Nicomachus of Gerasa |year=1926 |publisher=Macmillan }}</ref><ref>A History of Greek Mathematics, Heath, p. 70</ref> | Thales was known for introducing the theoretical and practical use of ] to Greece, and has been described as the first person in the western world to apply deductive reasoning to geometry, making him the West's "first mathematician."<ref name="books.google.com" /><ref>{{Harvnb|Boyer|1989|p=43 (3rd ed.)|edition=3rd}}</ref><ref name="gazette">{{cite journal |last=Fletcher |first=Colin R. |date=December 1982 |title=Thales – our founder? |journal=The Mathematical Gazette |volume=66 |issue=438 |page=267 |doi=10.2307/3615512 |jstor=3615512 |s2cid=125626522}}</ref> He is also credited with the West's oldest definition of ]: a "collection of units", "following the Egyptian view".<ref>{{Cite web |url=https://books.google.com/books?id=wdhMAAAAMAAJ |title=Introduction to Arithmetic|last=Nicomachus of Gerasa |year=1926 |publisher=Macmillan }}</ref><ref>A History of Greek Mathematics, Heath, p. 70</ref> | ||
| The evidence for the primacy of Thales comes to us from a book by ], who lived a thousand years afterward but is believed to have had a copy of ]'s lost book ''History of Geometry'' (4th century BC).{{efn|While some historians, such as Colin R. Fletcher, note there could have been a precursor to Thales named by Eudemus, without the work "the question becomes mere speculation."<ref name="gazette" /> Fletcher grants there is no other viable contender to the title of first Greek mathematician, and that Thales qualifies as a practitioner in the field. "Thales had at his command the techniques of observation, experimentation, superposition and deduction... he has proved himself mathematician."<ref name="gazette" />}} Proclus wrote that Thales was the first to visit Egypt and bring the Egyptian study of mathematics to Greece, and that Thales "himself discovered many propositions and disclosed the underlying principles of many others to his successors, in some case his method being more general, in others more empirical."<ref name="gazette" /> In addition to Proclus, ] also cites Thales as the first Greek mathematician. | The evidence for the primacy of Thales comes to us from a book by ], who lived a thousand years afterward but is believed to have had a copy of ]'s lost book ''History of Geometry'' (4th century BC).{{efn|While some historians, such as Colin R. Fletcher, note there could have been a precursor to Thales named by Eudemus, without the work "the question becomes mere speculation."<ref name="gazette" /> Fletcher grants there is no other viable contender to the title of first Greek mathematician, and that Thales qualifies as a practitioner in the field. "Thales had at his command the techniques of observation, experimentation, superposition and deduction... he has proved himself mathematician."<ref name="gazette" />}} Proclus wrote that Thales was the first to visit Egypt and bring the Egyptian study of mathematics to Greece, and that Thales "himself discovered many propositions and disclosed the underlying principles of many others to his successors, in some case his method being more general, in others more empirical."<ref name="gazette" /> In addition to Proclus, ] (3rd century BC) also cites Thales as the first Greek mathematician. | ||
| Proclus attributes to Thales the discovery that a circle is ] by its diameter, that the ] and that ] are equal.<ref name="bulmer-thomas">{{cite book |last=Bulmer-Thomas |first=Ivor |author-link=Ivor Bulmer-Thomas |year=1939 |title=Selections Illustrating the History of Greek Mathematics |volume=1 |chapter=Thales |pages=164–169 |publisher=Harvard University Press |chapter-url=https://archive.org/details/selectionsillust01bulmuoft/page/164/ }}</ref> Two fundamental ]s of elementary geometry are customarily called ''Thales's theorem'': ] has to do with a triangle inscribed in a circle and having the circle's diameter as one side;{{r|bulmer-thomas}} the other, also called the ], is about an angle intercepted by two parallel lines, forming a pair of ]. | Proclus attributes to Thales the discovery that a circle is ] by its diameter, that the ] and that ] are equal.<ref name="bulmer-thomas">{{cite book |last=Bulmer-Thomas |first=Ivor |author-link=Ivor Bulmer-Thomas |year=1939 |title=Selections Illustrating the History of Greek Mathematics |volume=1 |chapter=Thales |pages=164–169 |publisher=Harvard University Press |chapter-url=https://archive.org/details/selectionsillust01bulmuoft/page/164/ }}</ref> Two fundamental ]s of elementary geometry are customarily called ''Thales's theorem'': ] has to do with a triangle inscribed in a circle and having the circle's diameter as one side;{{r|bulmer-thomas}} the other, also called the ], is about an angle intercepted by two parallel lines, forming a pair of ]. | ||
Revision as of 20:02, 23 July 2024
Ancient Greek philosopher (c. 624 – c. 545 BC) "Thales" redirects here. For the company, see Thales Group. For other uses, see Thales (disambiguation).
| Thales of Miletus | |
|---|---|
 Posthumous portrait of Thales by Wilhelm Meyer, based on a bust from the 4th century Posthumous portrait of Thales by Wilhelm Meyer, based on a bust from the 4th century | |
| Born | c. 626/623 BC Miletus, Ionian League (modern-day Balat, Didim, Aydın, Turkey) |
| Died | c. 548/545 BC (aged c. 78) |
| Era | Pre-Socratic philosophy |
| Region | Western philosophy |
| School | Ionian / Milesian |
| Main interests | |
| Notable ideas | |
Thales of Miletus (/ˈθeɪliːz/ THAY-leez; Template:Lang-grc-gre; c. 626/623 – c. 548/545 BC) was an Ancient Greek pre-Socratic philosopher from Miletus in Ionia, Asia Minor. Thales was one of the Seven Sages, founding figures of Ancient Greece.
Many regard him as the first philosopher in the Greek tradition, breaking from the prior use of mythology to explain the world and instead using natural philosophy. He is thus otherwise referred to as the first to have engaged in mathematics, science, and deductive reasoning.
The first philosophers followed him in explaining all of nature as based on the existence of a single ultimate substance. Thales theorized that this single substance was water. Thales thought the Earth floated on water.
In mathematics, Thales is the namesake of Thales's theorem, and the intercept theorem can also be known as Thales's theorem. Thales was said to have calculated the heights of the pyramids and the distance of ships from the shore. In science, Thales was an astronomer who reportedly predicted the weather and a solar eclipse. The discovery of the position of the constellation Ursa Major is also attributed to Thales, as well as the timings of the solstices and equinoxes. He was also an engineer, known for having diverted the Halys River.
Life

The main source concerning the details of Thales's life and career is the doxographer Diogenes Laërtius, in his third century AD work Lives and Opinions of the Eminent Philosophers. While it is all we have, Diogenes wrote some eight centuries after Thales's death and his sources often contained "unreliable or even fabricated information." It is known Thales was from Miletus, a mercantile city settled at the mouth of the Maeander river.
The dates of Thales's life are not exactly known, but are roughly established by a few datable events mentioned in the sources. According to the historian Herodotus, writing in the 5th century BC, Thales predicted a solar eclipse in 585 BC. Assuming one's acme occurred at the age of 40, the chronicle of Apollodorus of Athens, written during the 2nd century BC, therefore placed Thales's birth about the year 625 BC.
Ancestry and family

While the probability is that Thales was as Greek as most Milesians, Herodotus described Thales as "a Phoenician by remote descent". Diogenes Laërtius references Herodotus, Duris, and Democritus, who all agree "that Thales was the son of Examyas and Cleobulina, and belonged to the Thelidae who are Phoenicians and amongst the noblest descendants of Cadmus and Agenor" who had been banished from Phoenicia and that Thales was enrolled as a citizen in Miletus along with Neleus.
However, Friedrich Nietzsche and others interpret this quote as meaning only that his ancestors were seafaring Cadmeians from Boeotia. It is also possible that he was of mixed ancestry, given his father had a Carian name and his mother had a Greek name. Diogenes Laërtius seems to also reference an alternative account: "Most writers, however, represent him as a genuine Milesian and of a distinguished family". Encyclopedia Britannica (1952) concluded that Thales was most likely a native Milesian of noble birth and that he was certainly a Greek.
Diogenes continues, by delivering more conflicting reports: one that Thales married and either fathered a son (Cybisthus or Cybisthon) or adopted his nephew of the same name; the second that he never married, telling his mother as a young man that it was too early to marry, and as an older man that it was too late. Plutarch had earlier told this version: Solon visited Thales and asked him why he remained single; Thales answered that he did not like the idea of having to worry about children. Nevertheless, several years later, anxious for family, he adopted his nephew Cybisthus.
Travels
The culture of Archaic Greece was heavily influenced by those of the Levant and Mesopotamia. It is said Thales was engaged in trade and visited either Egypt or Babylonia. However, there is no strong evidence that Thales ever visited countries in the Near East, and the issue is disputed among scholars. Visits to such places were a commonplace attribution to various philosophers by later writers, especially when these writers tried to explain the origin of their mathematical knowledge, such as with Thales or Pythagoras or Eudoxus.
Egypt

Several ancient authors assume that Thales, at one point in his life, visited Egypt, where he learned about geometry. It is considered possible that Thales visited Egypt, since Miletus had a permanent colony there (namely Naucratis). It is also said Thales had close contacts with the priests of Thebes who instructed him, or even that he instructed them in geometry. It is also possible Thales knew about Egypt from accounts of others, without actually visiting it.
Babylon
Aside from Egypt, the other mathematically advanced, ancient civilization before the Greeks was Babylonia, another commonplace attribution of travel for a mathematically-minded philosopher. At least one ancient historian, Josephus, claims Thales visited Babylonia.
Historians Roger L. Cooke and B.L. Van der Waerden come down on the side of Babylonian mathematics influencing the Greeks, citing the use of e. g. the sexagesimal system (or base 60). Cooke notes "This relation, however, is controversial." Others historians, such as D. R. Dicks, take issue with the idea of Babylonian influence on Greek mathematics. For until around the time of Hipparchus (c. 190–120 BC) their sexagesimal system was unknown.
Herodotus wrote the Greeks learnt the gnomon from the Babylonians. Thales's follower Anaximander is credited with introducing the gnomon to the Greeks. Herodotus also wrote that the practice of dividing the day into 12 parts, and the polos, came to the Greeks from the Babylonians. Yet this too is disputed, for example by historian L. Zhmud, who points out the gnomon was known to both Egyptians and Babylonians, the division of the day into twelve parts (and by analogy the year) was known to the Egyptians already in the 2nd millennium BC, and the idea of the polos was not used outside of Greece at this time.
Sagacity

Thales is recognized as one of the Seven Sages of Greece, semi-legendary wise statesmen and founding figures of Ancient Greece. While which seven one chooses may change, the seven has a canonical four which includes Thales, Solon of Athens, Pittacus of Mytilene, and Bias of Priene. Diogenes Laërtius tells us that the Seven Sages were created in the archonship of Damasius at Athens about 582 BC and that Thales was the first sage.
The sages were associated with the Delphic maxims, a quote or maxim attributed to each one inscribed on the Temple of Apollo at Delphi. Thales has arguably the most famous of all, gnothi seauton or know thyself. According to the 10th-century Byzantine encyclopedia the Suda, the proverb is both "applied to those whose boasts exceed what they are" and "a warning to pay no attention to the opinion of the multitude."
Golden tripod
Diogenes Laërtius relates several stories of an expensive, gold tripod or bowl that is to go to the most wise. In one version (that Laërtius credits to Callimachus in his Iambics) Bathycles of Arcadia states in his will that an expensive bowl "'should be given to him who had done most good by his wisdom.' So it was given to Thales, went the round of all the sages, and came back to Thales again. And he sent it to Apollo at Didyma, with this dedication...'Thales the Milesian, son of Examyas to Delphinian Apollo after twice winning the prize from all the Greeks.'"
Diplomacy
According to Diogenes Laërtius, Thales gained fame as a counselor when he advised the Milesians not to engage in a symmachia, a "fighting together", with the Lydians. This has sometimes been interpreted as an alliance.
Croesus was defeated before the city of Sardis by Cyrus the Great, who subsequently spared Miletus because it had taken no action. Cyrus was so impressed by Croesus’ wisdom and his connection with the sages that he spared him and took his advice on various matters. The Ionian cities should be demoi, or "districts".
He counselled them to establish a single seat of government, and pointed out Teos as the fittest place for it; "for that," he said, "was the centre of Ionia. Their other cities might still continue to enjoy their own laws, just as if they were independent states."
Miletus, however, received favorable terms from Cyrus. The others remained in an Ionian League of twelve cities (excluding Miletus), and were subjugated by the Persians.
Theories and studies
Early Greeks, and other civilizations before them, often invoked idiosyncratic explanations of natural phenomena with reference to the will of anthropomorphic gods and heroes. Instead, Thales aimed to explain natural phenomena via rational hypotheses that referenced natural processes themselves. Logos rather than mythos. Many, most notably Aristotle, regard him as the first philosopher in the Greek tradition. Rather than theologoi or mythologoi, Aristotle referred to the first philosophers as physiologoi, or natural philosophers, and Thales as the first among them. Also, while the other Seven Sages were strictly law-givers and statesmen and not speculative philosophers, Plutarch noted "it would seem that Thales was the only wise man of the time who carried his speculations beyond the realm of the practical."
Water is the arche
See also: Classical element § Hellenistic philosophy
Thales's most famous idea was his philosophical and cosmological thesis that all is water, which comes down to us through a passage from Aristotle's Metaphysics. In the work, Aristotle reported Thales's theory that the arche or originating principle of nature was a single material substance: water. Aristotle then proceeded to proffer a number of conjectures based on his own observations to lend some credence to why Thales may have advanced this idea (though Aristotle did not hold it himself).
While Aristotle's conjecture on why Thales held water as the originating principle of matter is his own thinking, his statement that Thales held it as water is generally accepted as genuinely originating with Thales. Writing centuries later, Diogenes Laërtius also states that Thales taught "Water constituted (ὑπεστήσατο, 'stood under') the principle of all things."
According to Aristotle:
That from which is everything that exists and from which it first becomes and into which it is rendered at last, its substance remaining under it, but transforming in qualities, that they say is the element and principle of things that are. …For it is necessary that there be some nature (φύσις), either one or more than one, from which become the other things of the object being saved... do not all agree as to the number and the nature of these principles. Thales the founder of this type of philosophy says that it is water.
Aristotle further adds:
Presumably he derived this assumption from seeing that the nutriment of everything is moist, and that heat itself is generated from moisture and depends upon it for its existence (and that from which a thing is generated is always its first principle). He derived his assumption from this; and also from the fact that the seeds of everything have a moist nature, whereas water is the first principle of the nature of moist things."
The 1870 book Dictionary of Greek and Roman Biography and Mythology noted:
In his dogma that water is the origin of things, that is, that it is that out of which every thing arises, and into which every thing resolves itself, Thales may have followed Orphic cosmogonies, while, unlike them, he sought to establish the truth of the assertion. Hence, Aristotle, immediately after he has called him the originator of philosophy brings forward the reasons which Thales was believed to have adduced in confirmation of that assertion; for that no written development of it, or indeed any book by Thales, was extant, is proved by the expressions which Aristotle uses when he brings forward the doctrines and proofs of the Milesian. (p. 1016)
Most agree that Thales's stamp on thought is the unity of substance. Not merely the empirical claim that all is water, but the deeper philosophical claim that all is one. For example, Friedrich Nietzsche, in his Philosophy in the Tragic Age of the Greeks, wrote:
Greek philosophy seems to begin with an absurd notion, with the proposition that water is the primal origin and the womb of all things. Is it really necessary for us to take serious notice of this proposition? It is, and for three reasons. First, because it tells us something about the primal origin of all things; second, because it does so in language devoid of image or fable, and finally, because contained in it, if only embryonically, is the thought, "all things are one."
Mathematics
—attributed to ThalesMegiston topos: apanta gar chorei
(Μέγιστον τόπος· ἄπαντα γὰρ χωρεῖ.)The greatest is space, for it holds all things.
Thales was known for introducing the theoretical and practical use of geometry to Greece, and has been described as the first person in the western world to apply deductive reasoning to geometry, making him the West's "first mathematician." He is also credited with the West's oldest definition of number: a "collection of units", "following the Egyptian view".
The evidence for the primacy of Thales comes to us from a book by Proclus, who lived a thousand years afterward but is believed to have had a copy of Eudemus's lost book History of Geometry (4th century BC). Proclus wrote that Thales was the first to visit Egypt and bring the Egyptian study of mathematics to Greece, and that Thales "himself discovered many propositions and disclosed the underlying principles of many others to his successors, in some case his method being more general, in others more empirical." In addition to Proclus, Hieronymus of Rhodes (3rd century BC) also cites Thales as the first Greek mathematician.
Proclus attributes to Thales the discovery that a circle is bisected by its diameter, that the base angles of an isosceles triangle are equal and that vertical angles are equal. Two fundamental theorems of elementary geometry are customarily called Thales's theorem: one of them has to do with a triangle inscribed in a circle and having the circle's diameter as one side; the other, also called the intercept theorem, is about an angle intercepted by two parallel lines, forming a pair of similar triangles.
Modern scholars are skeptical that anyone in Thales's time was producing mathematical proofs to the standard of later Greek mathematics, though not enough direct evidence remains to draw firm conclusions. While Thales may have discovered some basic geometric relations and provided some justification for them, attribution to him of formal proofs is now thought to represent speculative rationalization and reconstruction by later authors, rather than concrete accomplishments of Thales himself or his contemporaries.
Vertical angles
According to one author, while visiting Egypt, Thales observed that when the Egyptians drew two intersecting lines, they would measure the vertical angles to make sure that they were equal. Thales concluded that one could prove that all vertical angles are equal if one accepted some general notions such as: all straight angles are equal, equals added to equals are equal, and equals subtracted from equals are equal.
Right triangle inscribed in a circle
Main article: Thales's theorem
Pamphila says that, having learnt geometry from the Egyptians, Thales was the first to inscribe in a circle a right-angled triangle, whereupon he sacrificed an ox. This is sometimes cited as history's first mathematical discovery. Due to the variations among testimonies, such as the story of the ox sacrifice being accredited to Pythagoras upon discovery of the Pythagorean theorem rather than Thales, some historians (such as D. R. Dicks) question whether such anecdotes have any historical worth whatsoever.
It is believed the Babylonians knew the theorem for special cases. The theorem is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. Dante's Paradiso refers to Thales's theorem in the course of a speech.
Similar triangles
Main article: Intercept theorem
The story is told in Diogenes Laërtius, Pliny the Elder, and Plutarch, sourced from Hieronymus of Rhodes, that when Thales visited Egypt, he measured the height of the pyramids by their shadows at the moment when his own shadow was equal to his height. According to Plutarch, it pleased the pharoah Amasis. More practically, Thales was said to have the ability to measure the distances of ships at sea.
These stories indicate familiarity with the intercept theorem, and for this reason the 26th proposition in the first book of Euclid's Elements was attributed to Thales. They also indicate that he was familiar with the Egyptian seked, or seqed, the ratio of the run to the rise of a slope (cotangent). According to Kirk & Raven, all you need for this feat is three straight sticks pinned at one end and knowledge of your altitude. One stick goes vertically into the ground. A second is made level. With the third you sight the ship and calculate the seked from the height of the stick and its distance from the point of insertion to the line of sight.
Astronomy

Thales was also a noted astronomer, acknowledged in antiquity for describing the position of Ursa Minor, and he thought the constellation might be useful as a guide for navigation at sea. He calculated the duration of the year and the timings of the equinoxes and solstices. He is additionally attributed with calculating the position of the Pleiades.
Plutarch indicates that in his day (c. AD 100) there was an extant work, the Astronomy, composed in verse and attributed to Thales. While some say he left no writings, others say that he wrote On the Solstice and On the Equinox. The Nautical Star-guide has also been attributed to him, but this was disputed even in ancient times. No writing attributed to him has survived. Lobon of Argus asserted that the writings of Thales amounted to two hundred lines.
Cosmological model
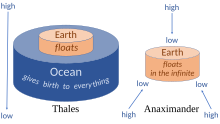
Thales thought the Earth must be a flat disk or mound of land and dirt which is floating in an expanse of water. Heraclitus Homericus states that Thales drew his conclusion from seeing moist substance turn into air, slime and earth. It seems likely that Thales viewed the land as coming from the water on which it floated and the oceans that surround it, perhaps inspired by observing silt deposits.
He thought the stars were balls of dirt on fire. He seemed to correctly gather that the moon reflects the Sun's light. A crater on the Moon is named in his honor.
Meteorology
Rather than assuming that earthquakes were the result of supernatural whims, Thales explained them by theorizing that the Earth floats on water and that earthquakes occur when the Earth is rocked by waves. He is attributed with the first observation of the Hyades, supposed by the ancients to indicate the approach of rain when they rose with the Sun. According to Seneca, Thales explained the flooding of the Nile as due to the river being beaten back by the etesian wind.
Olive presses

A story, with different versions, recounts how Thales achieved riches from an olive harvest by prediction of the weather. In one version, he bought all the olive presses in Miletus after predicting the weather and a good harvest for a particular year. Another version of the story has Aristotle explain that Thales had reserved presses in advance, at a discount, and could rent them out at a high price when demand peaked, following his prediction of a particularly good harvest. This first version of the story would constitute the first historically known creation and use of futures, whereas the second version would be the first historically known creation and use of options.
Aristotle explains that Thales's objective in doing this was not to enrich himself but to prove to his fellow Milesians that philosophy could be useful, contrary to what they thought, or alternatively, Thales had made his foray into enterprise because of a personal challenge put to him by an individual who had asked why, if Thales was an intelligent famous philosopher, he had yet to attain wealth.
Prediction of solar eclipse
Main article: Eclipse of ThalesAs mentioned above, according to Herodotus, Thales predicted a solar eclipse which occurred during a battle between the Lydians and the Medes. Among eclipses of the era, only the eclipse of 28 May 585 BC reached totality in Anatolia where the war took place. American writer Isaac Asimov described this battle as the earliest historical event whose date is known with precision to the day, and called the prediction "the birth of science". As well as first mathematician and first philosopher, Thales is often given the label of the first western scientist and the "father of science". but some contemporary scholars reject this interpretation.

Herodotus writes that in the sixth year of the war, the Lydians under King Alyattes and the Medes under Cyaxares were engaged in an indecisive battle when suddenly day turned into night, leading to both parties halting the fighting and negotiating a peace agreement. Herodotus also mentions that the loss of daylight had been predicted by Thales. He does not, however, mention the location of the battle.
Afterwards, on the refusal of Alyattes to give up his suppliants when Cyaxares sent to demand them of him, war broke out between the Lydians and the Medes, and continued for five years, with various success. In the course of it the Medes gained many victories over the Lydians, and the Lydians also gained many victories over the Medes. Among their other battles there was one night engagement. As, however, the balance had not inclined in favour of either nation, another combat took place in the sixth year, in the course of which, just as the battle was growing warm, day was on a sudden changed into night. This event had been foretold by Thales, the Milesian, who forewarned the Ionians of it, fixing for it the very year in which it actually took place. The Medes and Lydians, when they observed the change, ceased fighting, and were alike anxious to have terms of peace agreed on.
However, based on the list of Median kings and the duration of their reign reported elsewhere by Herodotus, Cyaxares died 10 years before the eclipse.
D. R. Dicks joins other historians (F. Martini, J. L. E. Dreyer, O. Neugebauer) in rejecting the historicity of the eclipse story. Dicks links the story of Thales discovering the cause for a solar eclipse with Herodotus' claim that Thales discovered the cycle of the sun with relation to the solstices, and concludes "he could not possibly have possessed this knowledge which neither the Egyptians nor the Babylonians nor his immediate successors possessed."
Falling into a well
See also: The Astrologer who Fell into a WellPlato, Diogenes Laertius, and Hippolytus all relay the story that Thales was so intent upon watching the stars that he failed to watch where he was walking, and fell into a well.
"Thales was studying the stars and gazing into the sky, when he fell into a well, and a jolly and witty Thracian servant girl made fun of him, saying that he was crazy to know about what was up in the heavens while he could not see what was in front of him beneath his feet."
Engineering

In addition to astronomy, Thales involved himself in other practical applications of mathematics, including engineering. Another story by Herodotus is that Croesus sent his army to the Persian territory. He was stopped by the river Halys, then unbridged. Thales then got the army across the river by digging a diversion upstream so as to reduce the flow, making it possible to cross the river. While Herodotus reported that most of his fellow Greeks believe that Thales did divert the river Halys to assist King Croesus' military endeavors, he himself finds it doubtful. Plato praises Thales along with Anacharsis, who is credited as the originator of the potter's wheel and the anchor.
Divinity

According to Aristotle, Thales thought "all things are full of gods", i. e. lodestones had souls, because iron is attracted to them (by the force of magnetism). The same applied to amber for its capacity to generate static electricity. The reasoning for such hylozoism or organicism seems to be if something moved, then it was alive, and if it was alive, then it must have a soul.
As well as gods seen in the movement caused by what came to be known as magnetism and electricity, it seems Thales also had a supreme God which structured the universe:
"Thales", says Cicero, "assures that water is the principle of all things; and that God is that Mind which shaped and created all things from water."
According to Henry Fielding (1775), Diogenes Laërtius (1.35) affirmed that Thales posed "the independent pre-existence of God from all eternity, stating "that God was the oldest of all beings, for he existed without a previous cause even in the way of generation; that the world was the most beautiful of all things; for it was created by God."
Nicholas Molinari has recently argued that Thales was influenced by the archaic water deity Acheloios, who was equated with water and worshipped in Miletus during Thales's life. For evidence, he points to the fact that hydor meant specifically "fresh water", and also that Acheloios was seen as a shape-shifter in myth and art, so able to become anything. He also points out that the rivers of the world were seen as the "sinews of Acheloios" in antiquity, and this multiplicity of deities is reflected in Thales's idea that "all things are full of gods."
Death and legacy
Diogenes Laërtius quotes Apollodorus as saying that Thales died at the age of 78 during the 58th Olympiad (548–545 BC) and attributes his death to heat stroke and thirst while watching the games.
Influence

As the first philosopher and mathematician, Thales had a profound influence on other Greek thinkers and therefore on Western history. However, due to the scarcity of sources concerning Thales and the discrepancies between the accounts given in the sources that have survived, there is a scholarly debate over the extent of the influence of Thales had and on which of the Greek philosophers and mathematicians that came after him.
The first three philosophers in the Western tradition were all cosmologists from Miletus, and Thales was the very first, followed by Anaximander, who was followed in turn by Anaximenes. They have been dubbed the Milesian school. According to the Suda, Thales had been the "teacher and kinsman" of Anaximander. Rather than water, Anaximander held all was made of apeiron or the unlimited; while Anaximenes, the successor of Anaximander, perhaps more like Thales with water, held that everything was composed of air.
John Burnet (1892) noted
Lastly, we have one admitted instance of a philosophic guild, that of the Pythagoreans. And it will be found that the hypothesis, if it is to be called by that name, of a regular organisation of scientific activity will alone explain all the facts. The development of doctrine in the hands of Thales, Anaximander, and Anaximenes, for instance, can only be understood as the elaboration of a single idea in a school with a continuous tradition.
As two of the first Greek mathematicians, Thales is also considered an influence on Pythagoras. According to Iamblichus, Pythagoras "had benefited by the instruction of Thales in many respects, but his greatest lesson had been to learn the value of saving time." Early sources report that Pythagoras, in this story a pupil of Anaximander, visited Thales as a young man, and that Thales advised him to travel to Egypt to further his philosophical and mathematical studies.
Thales was also considered the teacher of the astronomer Mandrolytus of Priene. It is possible he was also the teacher of Cleostratus of Tenedos.
Notes
- This use of hearsay and a lack of citing original sources leads some historians, like Dicks and Werner Jaeger, to view the whole idea of pre-Socratic philosophy as a construct from a later age, "fashioned during the two or three generations from Plato to the immediate pupils of Aristotle".
- In addition, his supposed mother, Cleobulina, has also been described as his companion instead of his mother.
- The exact meaning of this use of the word polos is unknown, current theories include: "the heavenly dome", "the tip of the axis of the celestial sphere", or a spherical concave sundial.
- The same story, however, asserts that Thales emigrated to Miletus; and that he did not become a student of nature until after his political career. This story has to be rejected if one is to believe that Thales was a native of Miletus, and other typical things about him like his prediction of the eclipse.
- The aphorism has also been attributed to various other philosophers. Diogenes Laërtius attributes it to Thales but notes that Antisthenes in his Successions of Philosophers attributes it instead to Phemonoe, a mythical Greek poet. The Roman poet Juvenal quotes the phrase in Greek and states that the precept descended e caelo (from heaven). Other names of potential include Pythagoras and Heraclitus.
- Historian Abraham Feldman wrote that for Thales "...water united all things...all whatness is wetness".
- Feldman notes "The social significance of water in the time of Thales induced him to discern through hardware and dry-goods, through soil and sperm, blood, sweat and tears, one fundamental fluid stuff...water, the most commonplace and powerful material known to him."
- While some historians, such as Colin R. Fletcher, note there could have been a precursor to Thales named by Eudemus, without the work "the question becomes mere speculation." Fletcher grants there is no other viable contender to the title of first Greek mathematician, and that Thales qualifies as a practitioner in the field. "Thales had at his command the techniques of observation, experimentation, superposition and deduction... he has proved himself mathematician."
- A right triangle with two equal legs is a 45-degree right triangle, all of which are similar. The length of the pyramid's shadow measured from the center of the pyramid at that moment must have been equal to its height.
- The seked is at the base of problems 56, 57, 58, 59 and 60 of the Rhind papyrus — an ancient Egyptian mathematical document.
- According to Diogenes Laertius, the Nautical Astronomy attributed to Thales was written by Phocus of Samos.
- The Scottish philosopher Adam Smith once similarly, absent-mindedly fell into a tannery pit.
- Edmund Husserl attempts to capture the new movement as follows. Philosophical man is a "new cultural configuration" based in stepping back from "pregiven tradition" and taking up a rational "inquiry into what is true in itself;" that is, an ideal of truth.
References
- ^ Russell, Bertrand (1945). A History of Western Philosophy. Simon & Schuster.
- Translation of his biography on Thales: Thales Archived 9 February 2008 at the Wayback Machine, classicpersuasion site; original Greek text, under ΘΑΛΗΣ, the Library of Ancient Texts Online site.
- See McKirahan, Richard D. Jr. (1994). Philosophy Before Socrates. Indianapolis: Hackett. p. 5. ISBN 978-0-87220-176-7.
- Jaeger, Werner (1948). Aristotle (2nd ed.). p. 454.
- ^ Herodotus, 1.74.2, and A. D. Godley's footnote 1; Pliny, 2.9 (12) and Bostock's footnote 2.
- Cohen, Mark S.; Curd, Patricia; Reeve, C. D. C. (2011). Readings in Ancient Greek Philosophy (Fourth Edition): From Thales to Aristotle. Indianapolis, Indiana: Hackett Publishing. p. 10. ISBN 978-1603846073.
- ^ Frank N. Magill, The Ancient World: Dictionary of World Biography, Volume 1, Routledge, 2003 ISBN 1135457395
- ^ Kirk, G. S.; Raven, J. E. (1957). "Chapter II: Thales of Miletus". The Presocratic Philosophers. Cambridge University Press. pp. 74–98.
- Freely, John (2012). The Flame of Miletus: The Birth of Science in Ancient Greece (And How It Changed the World). London: I. B. Tauris & Co. Ltd. p. 7. ISBN 978-1-78076-051-3. Retrieved 1 October 2017.
- Lawson, Russell M. (2004). Science in the Ancient World: An Encyclopedia. Santa Barbara, California; Denver, Colorado; and Oxford, England: ABC CLIO. pp. 234–235. ISBN 978-1-85109-534-6.
- Thatcher, Oliver J. (2004). The Library Of Original Sources: The Greek World. The Minerva Group, Inc. p. 138. ISBN 978-1-4102-1402-7.
- Nietzsche, Friedrich (2001). The Pre-Platonic Philosophers. University of Illinois Press. p. 23. ISBN 978-0252025594.
- ^ Alexander Herda. Burying a sage: the heroon of Thales in the agora of Miletos: With remarks on some other excavated Heroa and on cults and graves of the mythical founders of the city. 2èmes Rencontres d'archéologie de l'IFEA : Le Mort dans la ville Pratiques, contextes et impacts des inhumations intra-muros en Anatolie, du début de l'Age du Bronze à l'époque romaine., Nov 2011, Istanbul, Turkey. pp. 67–122
- ^ Yust, Walter (1952). Encyclopaedia Britannica: A New Survey of Universal Knowledge. Encyclopaedia Britannica. p. 13.
- Guthrie, W. K. C. (1978). A History of Greek Philosophy: The Earlier Presocratics and the Pythagoreans. Vol. 1. Cambridge University Press. p. 50. ISBN 978-0-521-29420-1.
- Goodman, Ellen (1995). The Origins of the Western Legal Tradition: From Thales to the Tudors. Federation Press. p. 9. ISBN 978-1-86287-181-6.
- Plant, I. M. (2004). Women Writers of Ancient Greece and Rome: An Anthology. Norman: University of Oklahoma Press. pp. 29–32.
- Plutarch (1952). "Solon". In Robert Maynard Hutchins (ed.). Lives. Great Books of the Western World. Vol. 14. Chicago: William Benton. p. 66.
- Riedweg, Christoph (2005) , Pythagoras: His Life, Teachings, and Influence, Ithaca, New York: Cornell University Press, ISBN 978-0-8014-7452-1 p. 7
- Plutarch, Life of Solon § 2.4
- O'Grady, Patricia F. (2017). Thales of Miletus: The Beginnings of Western Science and Philosophy. Taylor & Francis. p. 263. ISBN 978-1-351-89537-8.
- Hamlyn, David W. (2002). Being a Philosopher: The History of a Practice. Routledge. p. 7. ISBN 978-1-134-97101-5.
- ^ Russo, Lucio (2013). The Forgotten Revolution: How Science Was Born in 300 BC and Why it Had to Be Reborn. Translated by Levy, Silvio. Springer. p. 33. ISBN 978-3642189043.
- Harrison, Frederic (1892). The new calendar of great men: biographies of the 558 worthies of all ages. London and New York: MacMillan & Co. p. 92.
- Plutarch, On Isis And Osiris, ch. 10.
- Ferguson, Kitty (2011). Pythagoras: His Lives and the Legacy of a Rational Universe. Icon Books Ltd. p. 28. ISBN 978-1-84831-250-0.
- ^ Cooke, Roger L. (2005). The History of Mathematics: A Brief Course. John Wiley & Sons, Inc.
- ^ Dicks, D. R. (November 1959). "Thales". The Classical Quarterly. 9 (2): 294–309. doi:10.1017/S0009838800041586. S2CID 246881067.
- Diogenes Laertius (II, 1)
- "LacusCurtius • Ancient Astronomy: Polus (Smith's Dictionary, 1875)". penelope.uchicago.edu.
- Zhmud, Leonid (2006). The Origin of the History of Science in Classical Antiquity. Die Deutsche Bibliothek.
- Diogenes Laërtius 1.22
- "SOL Search". www.cs.uky.edu.
- Lives I.40
- "SOL Search". www.cs.uky.edu.
- Satires 11.27
- Vico, Giambattista; Visconti, Gian Galeazzo (1993). On humanistic education: (six inaugural orations, 1699–1707). Six Inaugural Orations, 1699–1707 From the Definitive Latin Text, Introduction, and Notes of Gian Galeazzo Visconti. Cornell University Press. p. 4. ISBN 0801480876.
- Doctoral thesis, "Know Thyself in Greek and Latin Literature," Eliza G. Wilkens, U. Chi, 1917, p. 12 (online).
- Laërtius 1925, § 28
- Diogenes Laërtius 1.25
- ^ Herodotus. The Histories. Translated by Rawlinson, George.
- ^ O'Grady, Patricia F. (2017). Thales of Miletus: The Beginnings of Western Science and Philosophy. Taylor & Francis. p. 102. ISBN 978-1-351-89536-1.
- ^ Aristotle, Metaphysics Alpha, 983b. http://data.perseus.org/citations/urn:cts:greekLit:tlg0086.tlg025.perseus-eng1:1.983b
- ^
 Smith, William, ed. (1870). "Thales". Dictionary of Greek and Roman Biography and Mythology. p. 1016.
Smith, William, ed. (1870). "Thales". Dictionary of Greek and Roman Biography and Mythology. p. 1016.
- Plutarch, Life of Solon, 3.5
- Diogenes Laërtius. Lives of the Eminent Philosophers. Book 1, paragraph 27.
- ^ Feldman, Abraham (October 1945). "Thoughts on Thales". The Classical Journal. 41 (1): 4–6. ISSN 0009-8353. JSTOR 3292119.
- Aristotle. "Book I 983b". Aristotle, Metaphysics. Perseus Project.
- § 3
- Laërtius 1925, § 35
- Boyer 1989, p. 43 (3rd ed.)
- ^ Fletcher, Colin R. (December 1982). "Thales – our founder?". The Mathematical Gazette. 66 (438): 267. doi:10.2307/3615512. JSTOR 3615512. S2CID 125626522.
- Nicomachus of Gerasa (1926). "Introduction to Arithmetic". Macmillan.
- A History of Greek Mathematics, Heath, p. 70
- ^ Bulmer-Thomas, Ivor (1939). "Thales". Selections Illustrating the History of Greek Mathematics. Vol. 1. Harvard University Press. pp. 164–169.
- Sidoli, Nathan (2018). "Greek mathematics" (PDF). In Jones, A.; Taub, L. (eds.). The Cambridge History of Science: Vol. 1, Ancient Science. Cambridge University Press. pp. 345–373.
- Shute, William George; Shirk, William W.; Porter, George F. (1960). Plane and Solid Geometry. American Book Company. pp. 25–27.
- Boyer 1989, p. "Ionia and the Pythagoreans" p. 43.
- de Laet, Siegfried J. (1996). History of Humanity: Scientific and Cultural Development. UNESCO, Volume 3, p. 14. ISBN 92-3-102812-X
- Boyer, Carl B. and Merzbach, Uta C. (2010). A History of Mathematics. John Wiley and Sons, Chapter IV. ISBN 0-470-63056-6
- Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements. Vol. 2 (Books 3–9) (2nd ed.). Dover. p. 61. ISBN 0486600890. Originally published by Cambridge University Press. 1st edition 1908, 2nd edition 1926.
- canto 13, lines 101–102
- Plutarch, Moralia, The Dinner of the Seven Wise Men, 147A
- J J O'Connor and E F Robertson
- "Ars Quatuor Coronatorum: Being the Transactions of the Quatuor Coronati Lodge No. 2076, London". W. J. Parre H, Limited. 10 June 1897.
- History of Astronomy, by Richard Perason, p. 65
- Proclus, In Euclidem, 352
- Plutarch, De Pythiae oraculis, 18.
- D.L. I.34
- Allman, George Johnston (1911). "Thales of Miletus" . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 26 (11th ed.). Cambridge University Press. p. 721.
- Harris, Roy (2005). The Semantics of Science. Continuum International. p. 31.
- Pseudo-Plutarch, Placita Philosopharum § 2.13
- Pseudo-Plutarch, Placita Philosopharum § 2.28
- Krech III, Shepard; Merchant, Carolyn; McNeill, John Robert, eds. (2003). "Earthquakes". Encyclopedia of World Environmental History. Vol. 1: A–G. Routledge. pp. 358–364.
- History of Meteorology to 1800 by H. Howard Frisinger p. 3
- Ibid, p. 4
- George Crawford, Bidyut Sen – Derivatives for Decision Makers: Strategic Management Issues, John Wiley & Sons, 1996 ISBN 978-0471129943
- Aristotle, Politics 1259a
- Singer, C. (2008). A Short History of Science to the 19th century. Streeter Press. p. 35.
- Needham, C. W. (1978). Cerebral Logic: Solving the Problem of Mind and Brain. Loose Leaf. p. 75. ISBN 978-0-398-03754-3.
- Finkelberg, Aryeh (2017). Heraclitus and Thales' Conceptual Scheme: A Historical Study. Brill. p. 318, fn. 38. ISBN 978-9004338210.
- Herodotus: Histories 1,74,2 (online)
- Alden A. Mosshammer: Thales' Eclipse. Transactions of the American Philological Association, Vol. 111, 1981, pp. 145–155 (JSTOR)
- Wenskus, Otta (2016). "Die angebliche Vorhersage einer Sonnenfinsternis durch Thales von Milet. Warum sich diese Legende so hartnäckig hält und warum es wichtig ist, ihr nicht zu glauben" (PDF) (in German). pp. 2–17.
- Theaetetus (174 A)
- D.L. II.4–5
- Powell, Jim (1 March 1995). "Brilliant but Absent-Minded Adam Smith | Jim Powell". fee.org.
- Theaetetus 174a
- O'Connor, John J.; Robertson, Edmund F. "Thales of Miletus". MacTutor History of Mathematics Archive. University of St Andrews.
- Herodotus. "Ch. 75". Herodotus. Translated by Godley, A. D. Harvard University Press.
- Plato, Republic, Book 10, section 600a
- Aristotle. De Anima. p. 411a7.
- Nathan Ida, Engineering Electromagnetics, Springer, 2015 ISBN 3319078062
- Sandywell, Barry (1996). Presocratic Reflexivity: The Construction of Philosophical Discourse C. 600-450 BC. Psychology Press. p. 97. ISBN 978-0-415-10170-7.
- Farrington, B., 1944 Greek Science. Pelican
- Cicero. De Natura Deorum. p. i.,10.
- Fielding, Henry (1775). An essay on conversation. John Bell. p. 346.
- Nicholas J. Molinari, Acheloios, Thales, and the Origin of Philosophy: A Response to the Neo-Marxians. Oxford: Archaeopress, 2022 https://www.archaeopress.com/Archaeopress/Products/9781803270869; cf. also Nicholas J. Molinari, Concerning Water as the Archai: Acheloios, Thales, and the Origin of Philosophy. A Dissertation Providing Philosophical, Mythological, and Archaeological Responses to the Neo-Marxians, Doctoral Dissertation, Newport, RI: Salve Regina University, 2020 https://philpapers.org/rec/MOLCWA-2
- Diogenes Laërtius. "Lives of Eminent Philosophers".
- The Vienna Lecture
- Kirk, G. S. (1960). "Popper on Science and Presocratics". Mind. New Series. 67 (275): 330. doi:10.1093/mind/LXIX.275.318. JSTOR 2251995.
- Graham, Daniel W. "Anaximenes (d. 528 B.C.E.)". IEP. Retrieved 20 July 2019.
- Burnet, John (1892). Early Greek Philosophy. A. and C. Black. p. 29.
- Life of Pythagoras 3.13
- Curnow, Trevor (22 June 2006). The Philosophers of the Ancient World: An A–Z Guide. A&C Black. ISBN 9780715634974.
- Webb, E. J. (1921). "Cleostratus Redivivus". The Journal of Hellenic Studies. 41: 70–85. doi:10.2307/624797. JSTOR 624797. S2CID 250254883.
Works cited
- Allman, George Johnston (1911). "Thales of Miletus" . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 26 (11th ed.). Cambridge University Press. p. 721.
- Boyer, C.B. (1989). A History of Mathematics (2nd ed.). New York: Wiley. ISBN 978-0-471-09763-1. (1991 pbk ed. ISBN 0-471-54397-7; 2011 3rd edition)
- Burnet, John (1957) . Early Greek Philosophy. The Meridian Library. Third Edition
 Laërtius, Diogenes (1925). "The Seven Sages: Thales" . Lives of the Eminent Philosophers. Vol. 1:1. Translated by Hicks, Robert Drew (Two volume ed.). Loeb Classical Library.
Laërtius, Diogenes (1925). "The Seven Sages: Thales" . Lives of the Eminent Philosophers. Vol. 1:1. Translated by Hicks, Robert Drew (Two volume ed.). Loeb Classical Library.- Herodotus, Histories, A. D. Godley (translator), Cambridge: Harvard University Press, 1920; ISBN 0-674-99133-8. Online version at Perseus
- Störig, Hans Joachim, Kleine Weltgeschichte der Philosophie. Fischer, Frankfurt/M. 2004, ISBN 3-596-50832-0.
- Lloyd, G. E. R. Early Greek Science: Thales to Aristotle.
- Nahm, Milton C. (1962) . Selections from Early Greek Philosophy. Appleton-Century-Crofts.
- Pliny the Elder, The Natural History (eds. John Bostock, M.D., F.R.S. H.T. Riley, Esq., B.A.) London. Taylor and Francis. (1855). Online version at the Perseus Digital Library.
- Turner, William (1913). "Ionian School of Philosophy" . In Herbermann, Charles (ed.). Catholic Encyclopedia. New York: Robert Appleton Company.
Further reading
- Couprie, Dirk L. (2011). Heaven and Earth in Ancient Greek Cosmology: from Thales to Heraclides Ponticus. Springer. ISBN 978-1441981158.
- Luchte, James (2011). Early Greek Thought: Before the Dawn. London: Bloomsbury Publishing. ISBN 978-0567353313.
- O'Grady, Patricia F. (2002). Thales of Miletus: The Beginnings of Western Science and Philosophy. Western Philosophy Series. Vol. 58. Ashgate. ISBN 978-0754605331.
- Mazzeo, Pietro (2010). Talete, il primo filosofo. Bari: Editrice Tipografica.
- Molinari, Nicholas J. (2022). Acheloios, Thales, and the Origin of Philosophy: A Response to the Neo-Marxians. Archaeopress. ISBN 9781803270869.
- Priou, Alex (2016). "'...Going Further On Down the Road...': The Origin and Foundations of Milesian Thought." The Review of Metaphysics 70, 3–31.
- Russell, Bertrand (1947). A History of Western Philosophy. Traditio Praesocratica. US: Simon & Schuster publisher. ISBN 0-415-32505-6.
- Wöhrle, Georg., ed. (2014). The Milesians: Thales. Translation and additional material by Richard McKirahan. Traditio Praesocratica. Vol. 1. Walter de Gruyter. ISBN 978-3-11-031525-7.
External links
- Thales of Miletus from The Internet Encyclopedia of Philosophy
- Thales of Miletus MacTutor History of Mathematics
- Thales' Theorem – Math Open Reference (with interactive animation)
- Thales biography by Charlene Douglass (with extensive bibliography)
- Thales of Miletus Life, Work and Testimonies by Giannis Stamatellos
- Thales Fragments
| Seven Sages of Greece | |
|---|---|
| Ancient Greek schools of philosophy | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Proto-philosophy |
| ||||||||||||||||||||||||||||
| Pre-Socratic |
| ||||||||||||||||||||||||||||
| Classical |
| ||||||||||||||||||||||||||||
| Hellenistic |
| ||||||||||||||||||||||||||||
| Ancient Greece | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||
- 6th-century BC Greek philosophers
- 620s BC births
- 540s BC deaths
- Ancient Greek astronomers
- Ancient Greek geometers
- Ancient Greek metaphysicians
- Ancient Greek physicists
- Ancient Milesians
- Epistemologists
- Metaphilosophers
- Metaphysicians
- Metaphysics writers
- Natural philosophers
- Ontologists
- Philosophers of ancient Ionia
- Philosophers of education
- Philosophers of mathematics
- Philosophers of mind
- Philosophers of science
- Presocratic philosophers
- Seven Sages of Greece
- 6th-century BC mathematicians
- 6th-century BC astronomers