| Revision as of 19:08, 26 December 2005 edit66.225.247.182 (talk)No edit summary← Previous edit | Revision as of 06:47, 27 December 2005 edit undoQutezuce (talk | contribs)13,755 editsm rv, while that book does sound interesting, it is not realNext edit → | ||
| Line 59: | Line 59: | ||
| * ''Knot Theory'', ], ], ISBN 0415310016 | * ''Knot Theory'', ], ], ISBN 0415310016 | ||
| * ''Introduction to Knot Theory'', ] and ], ], ISBN 0-387-90272-4 | * ''Introduction to Knot Theory'', ] and ], ], ISBN 0-387-90272-4 | ||
| * ''Why I hate the fourth dimension & how to make money refurnishing others apartments : and other paradoxical relationships '', ] and ], ], ISBN 0763619507 | |||
| * ''Knots and Links'', ], ], ISBN 0-914098-16-0 | * ''Knots and Links'', ], ], ISBN 0-914098-16-0 | ||
| * ''On Knots'', ], ], ISBN 0-691-08435-1 | * ''On Knots'', ], ], ISBN 0-691-08435-1 | ||
| Line 65: | Line 64: | ||
| * The wiki . | * The wiki . | ||
| * | * | ||
| ==References== | ==References== | ||
Revision as of 06:47, 27 December 2005

Knot theory is a branch of topology inspired by observations, as the name suggests, of knots. But progress in the field does not depend exclusively on experiments with twine. Knot theory concerns itself with abstract properties of theoretical knots — the spatial arrangements that in principle could be assumed by a loop of string.
When mathematical topologists consider knots and other entanglements such as links and braids, they describe how the knot is positioned in the space around it, called the ambient space. If the knot is moved smoothly to a different position in the ambient space, then the knot is considered to be unchanged, and if one knot can be moved smoothly to coincide with another knot, the two knots are called "equivalent".
In mathematical language, knots are embeddings of the circle in three-dimensional space. A mathematical knot thus resembles an ordinary knot with its ends spliced. The topological theory of knots investigates such questions as whether two knots can be smoothly moved to match one another, without opening the splice. The question of untying an ordinary knot has to do with unwedging tangles of rope pulled tight, but this concept plays at best a minor role in the mathematical theory. A knot can be untied in the topological sense if and only if it can be smoothly moved through the ambient space until it assumes the shape of a circle. If this can be done, the knot is called the unknot.
Modern knot theory has extended the concept of a knot to higher dimensions. One recent application of knot theory has been to the question of whether two strands of DNA are equivalent without cutting.

History
Knot theory originated in an idea of Lord Kelvin's (1867), that atoms were knots of swirling vortices in the æther. He believed that an understanding and classification of all possible knots would explain why atoms absorb and emit light at only the discrete wavelengths that they do. We now know that this idea was mistaken, and that the discrete wavelengths depend on quantum energy levels.
Scottish physicist Peter Tait spent many years listing unique knots in the belief that he was creating a table of elements. When the luminiferous æther was not detected in the Michelson-Morley experiment, vortex theory became completely obsolete, and knot theory ceased to be of great scientific interest. Following the development of topology in the late nineteenth century, knots once again became a popular field of study. Today, knot theory finds applications in string theory, in the study of DNA replication and recombination, and in areas of statistical mechanics.
An introduction to knot theory
Creating a knot is easy. Begin with a one-dimensional line segment, wrap it around itself arbitrarily, and then fuse its two free ends together to form a closed loop. One of the biggest unresolved problems in knot theory is to give a method to decide in every case whether two such embeddings are different or the same.
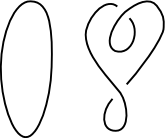 |
equivalent to it |
Before we can do this, we must decide what it means for embeddings to be "the same". We consider two embeddings of a loop to be the same if we can get from one to the other by a series of slides and distortions of the string which do not tear it, and do not pass one segment of string through another. If no such sequence of moves exists, the embeddings are different knots.
Knot diagrams
A useful way to visualise knots and the allowed moves on them is to project the knot onto a plane - think of the knot casting a shadow on the wall. Now we can draw and manipulate pictures, instead of having to think in 3D. However, there is one more thing we must do - at each crossing we must indicate which section is "over" and which is "under". This is to prevent us from pushing one piece of string through another, which is against the rules. To avoid ambiguity, we must avoid having three arcs cross at the same crossing and also having two arcs meet without actually crossing. When this is the case, we say that the knot is in general position with respect to the plane. Fortunately a small perturbation in either the original knot or the position of the plane is all that is needed to ensure this.
Reidemeister moves

In 1927, working with this diagrammatic form of knots, J.W. Alexander and G.B. Briggs, and independently Kurt Reidemeister, demonstrated that two knot diagrams belonging to the same knot can be related by a sequence of three kinds of moves on the diagram, shown right. These operations, now called the Reidemeister moves, are:
I. Twist and untwist in either direction.
II. Move one loop completely over another.
III. Move a string completely over or under a crossing.
Knot invariants can be defined by demonstrating a property of a knot diagram which is not changed when we apply any of the Reidemeister moves. Many important invariants can be defined in this way, including the Jones polynomial. Older examples of knot invariants include the fundamental group and the Alexander polynomial.
Higher dimensions
You can unknot any circle in four dimensions. There are two steps to this. First, "push" the circle into a 3-dimensional subspace. This is the hard, technical part which we will skip. Now imagine temperature to be a fourth dimension to the 3-dimensional space. Then you could make one section of a line cross through the other by simply warming it with your fingers.
In general piecewise-linear n-spheres form knots only in -space (a result of E.C. Zeeman), although one can have smoothly knotted n-spheres in -space for (independent results of A. Haefliger and J. Levine).
Adding knots
Two knots can be added by cutting both knots and joining the pairs of ends. This can be formally defined as follows: consider a planar projection of each knot and suppose these projections are disjoint. Find a rectangle in the plane where one pair of opposite sides are arcs along each knot while the rest of the rectangle is disjoint from the knots. Form a new knot by deleting the first pair of opposite sides and adjoining the other pair of opposite sides. The resulting knot is the sum of the original knots.
This operation is called the knot sum, or sometimes the connected sum or composition of two knots. Knots in 3-space form a commutative monoid with prime factorization, which allows us to define what is meant by a prime knot. The trefoil knot is the simplest prime knot. Higher dimensional knots can be added by splicing the n-spheres. While you cannot form the unknot in three dimensions by adding two non-trivial knots, you can in higher dimensions, at least when one considers smooth knots in codimension at least 3.
See also
- list of knot theory topics
- Borromean rings
- braid theory
- DNA topology
- Khipu
- knot invariant
- linking number
- topoisomerase
Further reading
- The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, Colin Adams, 2001, ISBN 0716742195
- Knots: Mathematics With a Twist, Alexei Sossinsky, 2002, ISBN 0674009444
- Knot Theory, Vassily Manturov, 2004, ISBN 0415310016
- Introduction to Knot Theory, Richard H. Crowell and Ralph Fox, 1977, ISBN 0-387-90272-4
- Knots and Links, Dale Rolfsen, 1976, ISBN 0-914098-16-0
- On Knots, Louis H. Kauffman, 1987, ISBN 0-691-08435-1
- Weisstein, Eric W. "Reidemeister Moves". MathWorld.
- The wiki Knot Atlas.
- KnotPlot
References
- Peterson, Mathematical Tourist, 1988, p74
- Knot Theory History : traces it a little further, to Gauss' analysis situs.
 -space (a result of E.C. Zeeman), although one can have smoothly knotted
-space (a result of E.C. Zeeman), although one can have smoothly knotted  -space for
-space for  (independent results of A. Haefliger and J. Levine).
(independent results of A. Haefliger and J. Levine).